基于精确Zoeppritz方程的储层含油气性预测方法
周林, 廖建平, 李景叶, 陈小宏, 刘兴业
1 湖南科技大学页岩气资源利用湖南省重点实验室,湘潭 411201 2 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249 3 中国石油大学(北京)海洋石油勘探国家工程实验室,北京 102249 4 西安科技大学地质与环境学院,西安 710054
0 引言
岩性和流体识别能够为储层含油气性预测提供关键信息,其中流体识别的精度会直接影响储层油气分布预测精度.因此,如何合理高效的对储层流体进行识别一直以来都是油藏勘探开发关注的重点,学者们也在这方面进行了大量研究.Smith和Gidlow(1987)通过联合纵横波速度首次定义了流体因子的概念并成功将其应用于含气砂岩储层的流体识别.Goodway等(1997)指出拉梅岩石物理常数λρ和μρ在流体检测和岩性识别方面明显优于纵横波速度.基于孔弹性理论(Biot, 1941; Gassman, 1951),Russell等(2003, 2011)定义了具有明确物理意义的流体因子f,即经典的Russell流体因子.Feng等(2007)通过对常用流体因子比较分析指出ρf在流体判别方面表现更好.Yin和Zhang(2014)将有效孔隙流体体积模量Kf定义为新的流体指示因子,有效提升了流体识别的灵敏度.然而,其研究成果显示,有效孔隙流体体积模量的引入会导致待反演的目标参数数量增加,这会严重影响非线性反演算法的稳定性和不确定性.李春宁(2014)构建了一个新的流体指示因子Fρ.相比于经典的Russell流体因子f和孔隙流体体积模量Kf,该流体因子不包含干岩石纵横波速度比.并且,冷雪梅等(2019)通过研究指出,该流体因子的流体识别效果与Russell流体因子非常接近.从上述研究可以看出,流体因子的种类繁多且各有优缺点,本文将根据后续反演算法的需求,并借助杨培杰等(2016)提出的敏感流体因子定量分析法对现有流体指示因子进行优选.由于储层的复杂性和多样性,如果脱离岩性指示信息的约束,仅依靠流体因子反演结果对储层含油气性进行预测可能会导致解释结果存在假象.如果能够同时得到对储层流体和岩性指示性明确的参数,共同对储层含油气性进行预测将会大大降低预测结果的不确定性.大量研究表明,泊松比具有良好的岩性和含油气性指示效果(樊长江和王贤, 2006; Ostrander, 1984; 宗兆云等, 2012b; Zong et al., 2013a;Zhou et al., 2017; Zong and Yin, 2017).因此,为了有效提升储层含油气性预测精度,本文将以流体因子和泊松比同时作为目标待反演参数.
叠前地震数据中包含着丰富的地下流体和岩性信息,因此叠前AVO/AVA反演技术被广泛应用于储层流体检测和岩性识别.Russell等(2011)推导了包含Russell流体因子、剪切模量和密度的线性近似公式,并采用标准最小二乘反演方法实现了线性反演.宗兆云等(2012a)、Zong等(2012)推导了包含纵波模量和横波模量的线性近似方程以及弹性阻抗方程,进而基于岩石物理关系实现了Russell流体因子的间接估算.李雷豪等(2019)从减少参数维数入手将上述包含纵横波模量的三项线性近似方程简化为两项式,提升了反演结果的稳定性,并最终通过间接计算实现了高敏流体识别因子的估计.为了避免间接计算造成的累积误差,Zong等(2013b)利用Russell线性近似方程基于贝叶斯理论实现了Russell流体因子的直接反演.宗兆云等(2012b)、Zong等(2013a)推导了包含杨氏模量和泊松比的近似公式,并实现了泊松比的直接反演.Du和Yan(2013)推导了包含ρf和ρμ的PP和PS波反射系数两项近似式,并基于这两个方程实现了纵横波联合反演.杜炳毅等(2016)基于Russell近似推导了PS波反射系数近似公式并实现了联合反演.Zong和Xin(2017)推导了包含杨氏阻抗和泊松阻抗的线性近似方程,并实现了基于该方程的叠前反演,有效提升了非常规储层流体和岩性的识别精度.Yin和Zhang(2014)、Zong等(2015)、Du等(2019)推导了包含孔隙流体体积模量的线性近似公式并实现了孔隙流体模量的线性反演.冷雪梅等(2019)推导了包含流体因子Fρ的弹性阻抗方程,并实现了基于该方程的联合反演.吴奎等(2021)从Russell近似表达式出发推导了包含Russell流体因子的弹性阻抗方程,并实现了基于该方程的流体因子反演预测.然而,上述反演方法均是以精确Zoeppritz方程的近似公式为正演算子.众所周知,近似公式推导过程中的诸多假设条件会极大地限制上述反演方法的应用效果,尤其是在具有强阻抗差异特征的储层.为了克服近似公式引入的一系列问题,本文将聚焦如何利用精确Zoeppritz方程实现流体因子和泊松比的直接反演.
基于贝叶斯理论构建反演目标函数,并在先验模型中有针对性地引入合理的先验分布特征能够进一步有效提升反演结果的精度(Alemie and Sacchi, 2011).Theune等(2010)、Zhou等(2020)通过研究指出,在先验模型中引入服从微分拉普拉斯分布的块约束项能够通过压制旁瓣来更好地表征储层边界.因此,本文将采用同样的策略来进一步提升流体因子和泊松比反演结果对储层边界的刻画效果.
本文首先对现有常用流体指示因子利用感流体因子定量分析法进行了优选,然后将传统形式的精确Zoeppritz方程改写为包含优选流体因子、泊松比和密度的新形式,并基于新形式的精确Zoeppritz方程构建了贝叶斯框架下的非线性反演目标函数,有效地避免了常规基于近似公式的反演方法对反演结果精度的限制.此外,为了进一步提升反演结果对储层边界的刻画效果,在先验模型中引入服从微分拉普拉斯分布的块约束项.合成数据和油田数据应用表明,新方法能够高精度地估计流体因子和泊松比,且最终能够基于二者反演结果实现储层油气分布特征的准确预测.
1 方法原理
1.1 流体因子敏感性分析

(1)
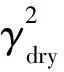
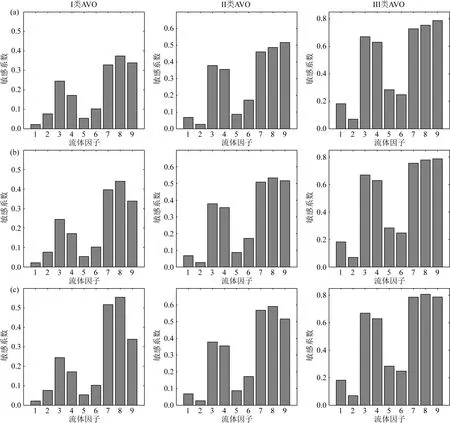
图1 流体因子敏感系数柱状图(第Ⅰ~Ⅲ类AVO含流体砂岩模型)
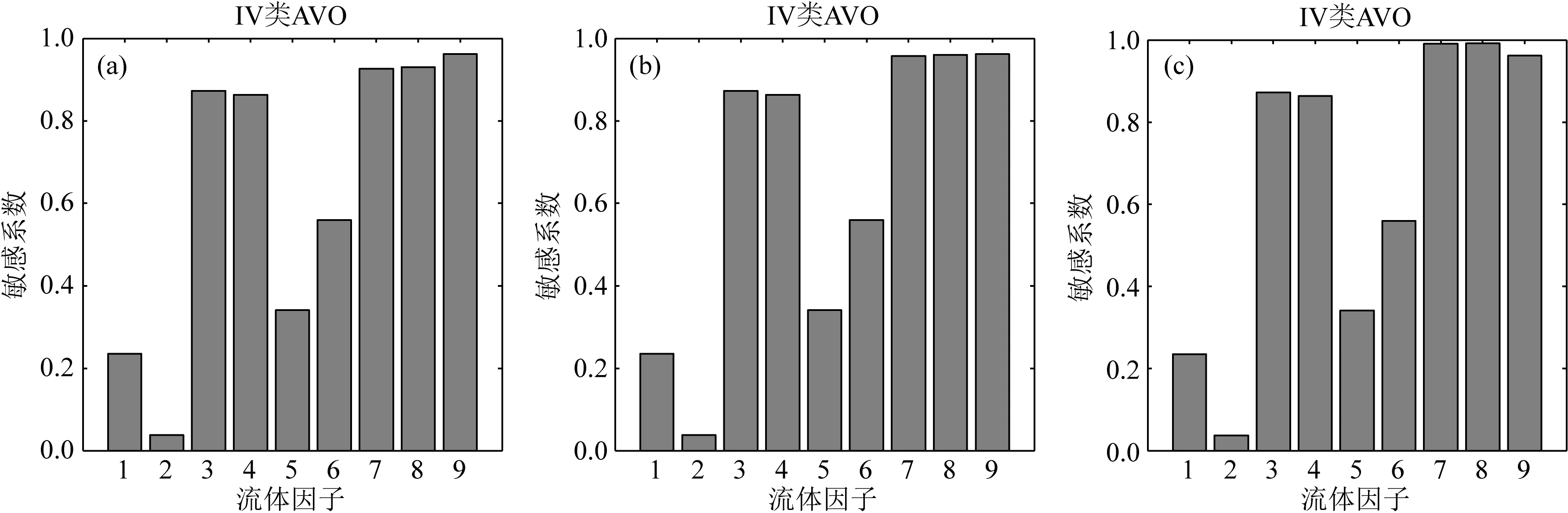
图2 流体因子敏感系数柱状图(第Ⅳ类AVO含流体砂岩模型)
(2)
1.2 包含流体因子Fρ、泊松比σ和密度ρ的新形式精确Zoeppritz方程推导
传统形式的精确Zoeppritz方程为(Zoeppritz, 1919; Aki and Richards, 1980):
(3)
式中,VP1、VP2、VS1、VS2、ρ1和ρ2分别表示反射界面两侧的纵横波速度和密度,θ1和θ2分别表示P波的入射角和透射角,φ1和φ2分别表示PS转换波的反射角和透射角,RPP和RPS分别表示P波和PS转换波的反射系数,TPP和TPS分别表示P波和PS转换波的透射系数.根据Snell定律可得:
(4)
将公式(4)代入公式(3)可得:
(5)
在各向同性介质中,纵波模量、杨氏模量与纵横波速度以及密度存在如下关系:
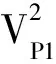
(6)
(7)
其中,M1和M2为上下层纵波模量,E1和E2为上下层杨氏模量.将公式(6)和(7)代入公式(2)可得:
Fρ1=ρ1M1-ρ1E1,Fρ2=ρ2M2-ρ2E2.
(8)
在各向同性介质中,纵横波模量与泊松比、杨氏模量存在如下岩石物理关系:
(9)
(10)
其中,σ1和σ2为上下层泊松比.将公式(9)代入公式(8)可得:
(11)
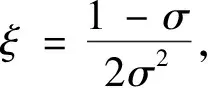
(12)
将公式(9)和(11)代入公式(10)可得:
(13)
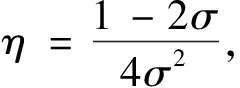
(14)
将公式(12)和(14)代入公式(5),即可得到包含流体因子Fρ、泊松比σ和密度ρ的新形式精确Zoeppritz方程:
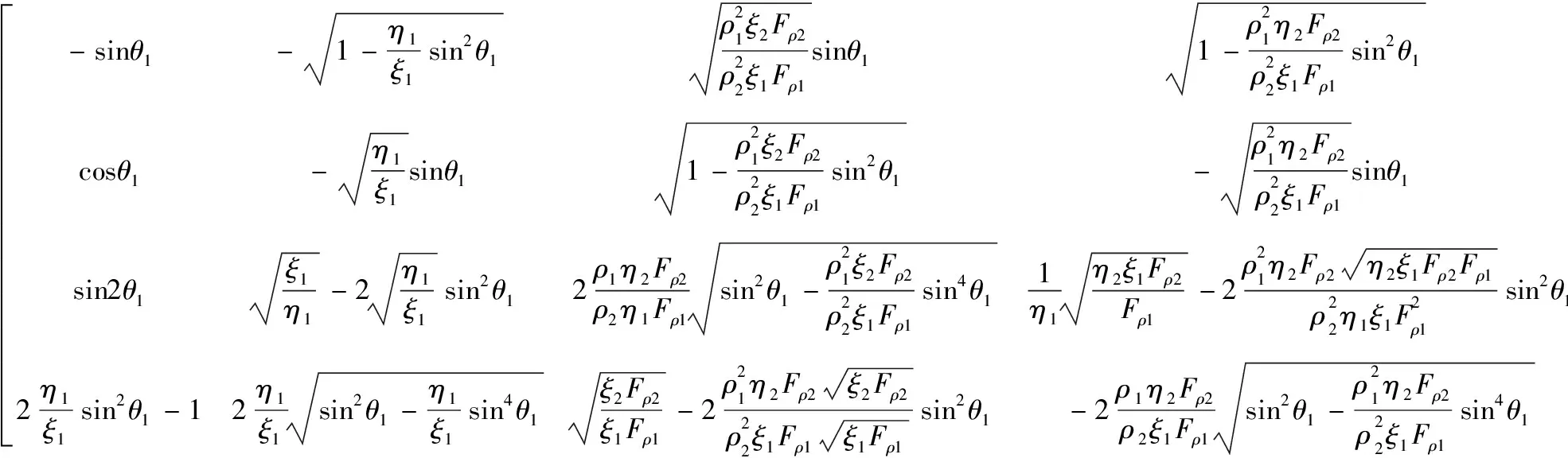
(15)
此外,为了便于其他学者对全文研究内容的重现以及后续反演算法的对比,本文在附录A中给出了包含流体因子Fρ、泊松比σ和密度ρ的传统线性近似公式的详细推导过程.
1.3 叠前AVA非线性反演
当精确Zoeppritz方程的参数化形式发生改变时,其为反演带来的不稳定性也会发生变化.因此,在反演之前我们借助残差函数图分析法对新方程的反演稳定性进行了分析(Larsen, 1999;Zhou et al., 2020),结果显示新方程的残差函数图都是光滑的,没有不规则的,且大部分都围绕单极值呈现闭合的等值线,根据Zhou等(2020)的研究可知,本文推导的新形式精确Zoeppritz方程不会为反演算法带来明显的不稳定性,能够成功地应用于贝叶斯确定性反演中.
以公式(15)所示新形式精确Zoeppritz方程为正演算子,构建贝叶斯理论框架下的非线性反演目标函数.假设似然函数P(d|m)服从高斯分布,则有:
(16)
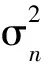
大量研究表明,如果存在质量可靠且匹配良好的多波数据,多波联合反演能够进一步降低反演的不确定性,提升反演结果的精度(Stewart, 1990; Lu et al., 2015; 周林等, 2016; Zhou et al., 2017).
对于多波数据,公式(16)可推广为:
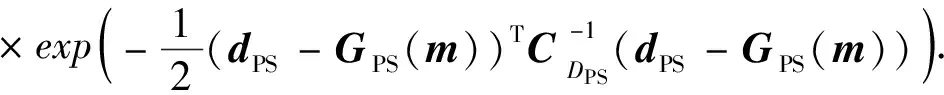
(17)
基于贝叶斯理论构建目标函数的优势是能够通过引入更加有针对性的先验分布模型进一步提升待反演参数的精度和分辨率.Theune等(2010)、Zhou等(2020)等学者指出,在先验模型中引入服从微分拉普拉斯分布的块约束项能够通过压制旁瓣来更好地表征储层边界.因此,为了进一步提升流体因子反演结果对储层流体边界以及泊松比反演结果对岩性边界的刻画能力,先验分布函数P(m)被定义为(Zhou et al., 2020):
(18)
其中,Cm为包含三个待反演参数之间统计相关性的协方差矩阵,μ为均值向量,D为一阶微分矩阵算子,kl(l=1,2,3)为尺度参数,每一个待反演参数对应一个尺度参数.
将公式(17)和(18)代入贝叶斯理论中,即可将求解最大后验概率解的问题转化为求解如下所示目标函数最小值的问题:
(19)
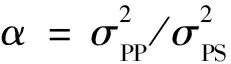
对于公式(19)所示非线性目标函数,通常可以采用高斯-牛顿法或借助泰勒级数展开对其进行快速稳定求解(周林等, 2016; Zhou et al., 2017),为了避免求解正演算子关于待反演参数的二阶偏导数,本文将借助泰勒级数展开的方法对上述目标函数进行求解.根据Zhou等(2017)的研究,对非线性正演方程G(m)进行泰勒级数展开并取其一阶近似,然后代入公式(19)可得:
(20)
此时,公式(20)所示目标函数就变成了一个关于目标参数扰动量Δm的线性方程,将公式(20)关于该扰动量求导并令导数等于零可得:
Δm=H-1γ,
(21)
其中:
基于上述求解表达式,我们可以得到目标参数更新项Δm0,从而实现对初始模型m0的更新:
m1=m0+Δm0.
(22)
将m1代入到公式(21),即利用更新后的模型参数m1替代初始模型m0,则又可以得到一个新的目标参数更新项Δm1,这样我们就可以实现模型参数的连续迭代更新,并最终达到最大迭代次数.因此,公式(19)所示目标函数的解可表示为:
Δmj=(H(mj))-1γ(mj),
(23)
其中:
最终,可得到如下所示待反演参数迭代更新公式:
mj+1=mj+λjΔmj,j=0,1,2,…,
(24)
其中,λj为第j次迭代的步长.
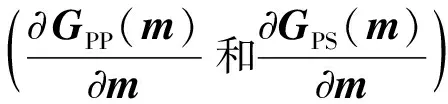
2 合成数据测试
为了验证基于新形式精确Zoeppritz方程流体因子、泊松比直接反演方法的可行性和稳定性,本文利用图3所示单井模型进行算法测试.图中黑线表示真实待反演参数,虚线表示初始模型参数.利用精确Zoeppritz方程基于图3黑线所示真实参数值计算得到对应的反射系数向量,并与主频为30 Hz的雷克子波进行褶积,最终得到如图4a所示不含噪声的合成PP波和PS波角道集数据.该角道集数据包含4°到40°之间的10个角度(以4°为间隔).为了测试算法的稳定性和抗噪性,在合成数据中加入均方根信噪比为0.5的随机噪声,如图4b所示.图5和图6分别为本文提出的基于新形式精确Zoeppritz方程流体因子、泊松比直接反演方法和基于传统近似公式反演方法的反演结果.其中,图5a和图6a为PP波单独反演的结果,图5b和图6b为PP-PS联合反演的结果.从图5和图6的对比可以看出,新方法的反演精度明显高于基于传统近似公式的常规方法.此外,从图5a、b对比可以看出,基于新形式精确Zoeppritz方程的联合反演能够进一步提升反演结果的精度.而图6a、b的对比显示,由近似公式计算得到的PS波反射系数存在较大误差,使得基于传统近似公式的联合反演不仅未能有效改善反演结果的精度甚至还在一定程度上降低了反演结果的精度.这说明新方法不仅反演精度优于常规方法,而且在PS波信息利用方面也表现的更好,充分验证了新方法的可行性和有效性.仔细观察图5和图6,我们还可以发现另外一个现象,即不管是传统方法,还是新方法,密度反演结果精度均低于流体因子和泊松比反演结果精度.对此,我们借助基于单一变量原则的参数变化敏感性分析手段进行了简要分析,发现包含流体因子、泊松比以及密度项的新方程对密度参数变化的敏感性明显低于流体因子和泊松比,这也很好地解释了这种现象的存在.
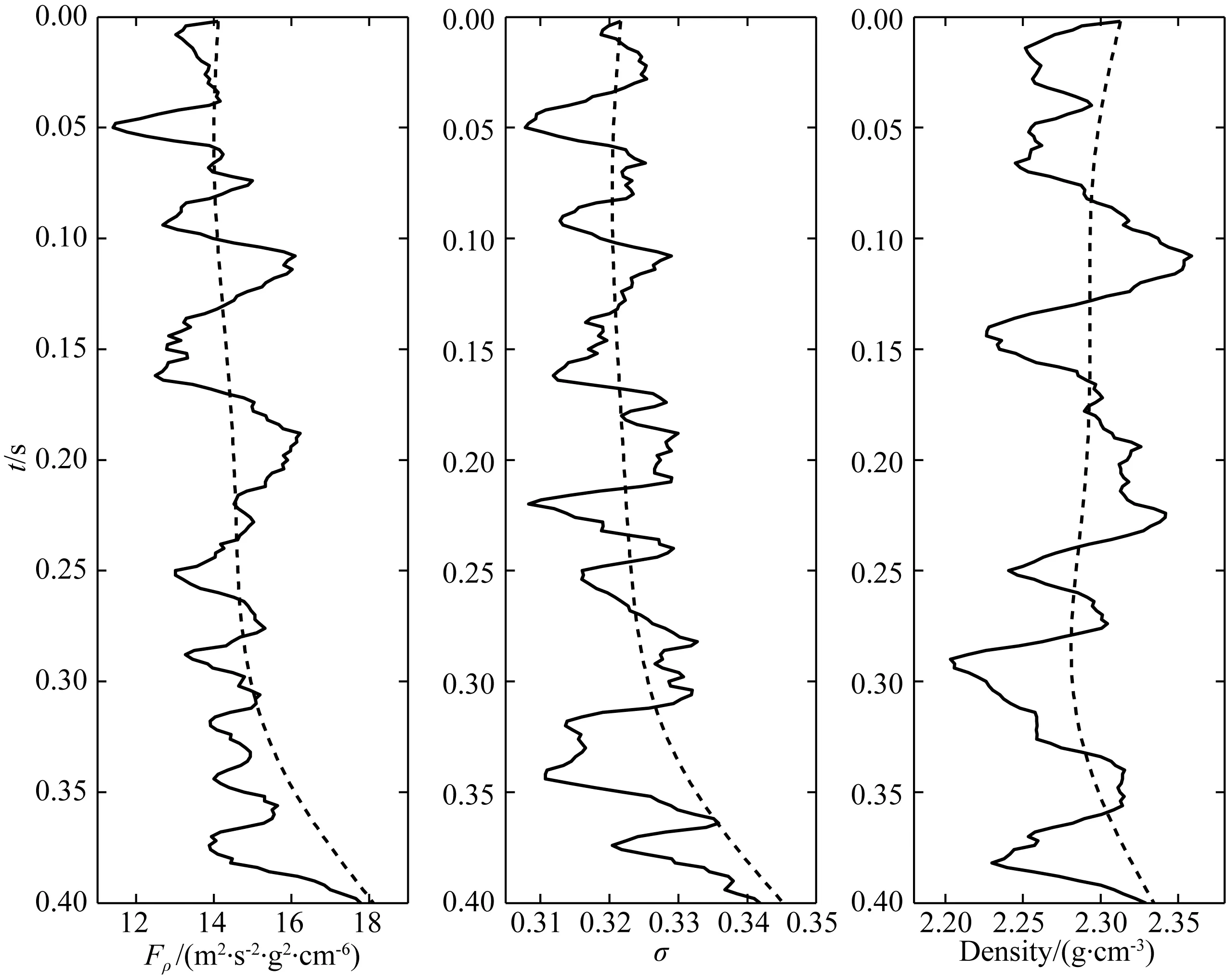
图3 单井模型
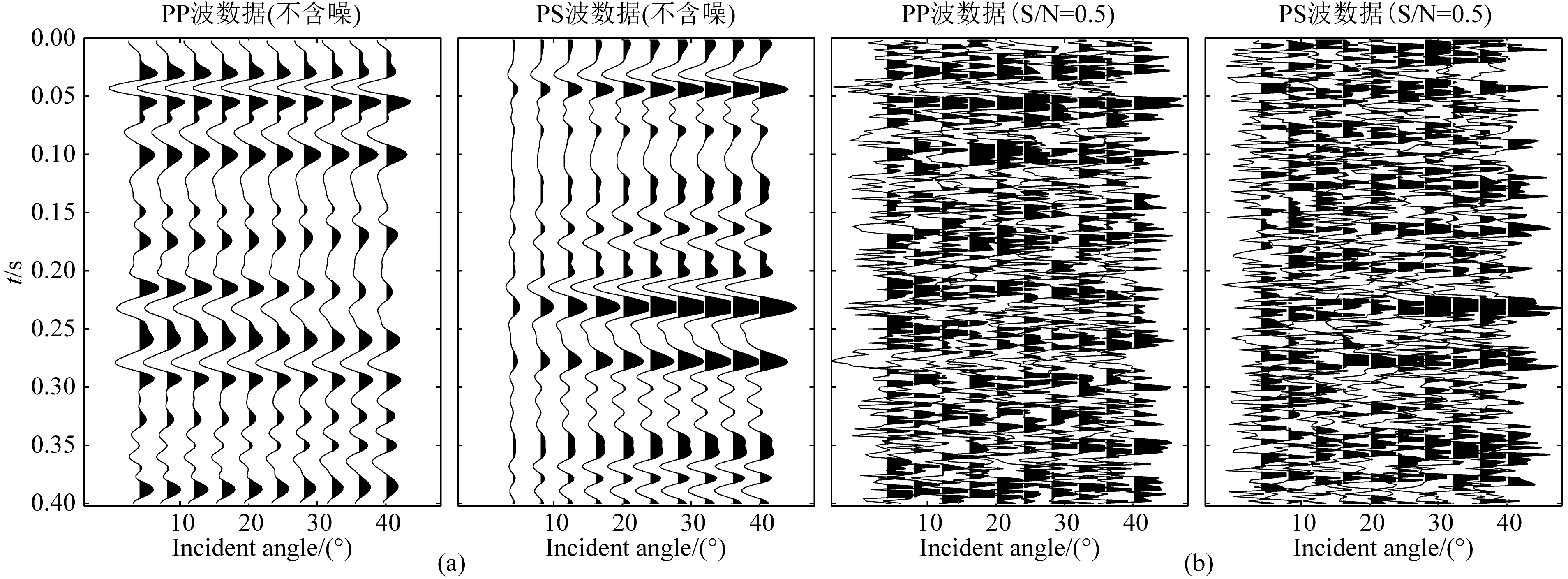
图4 合成叠前角道集
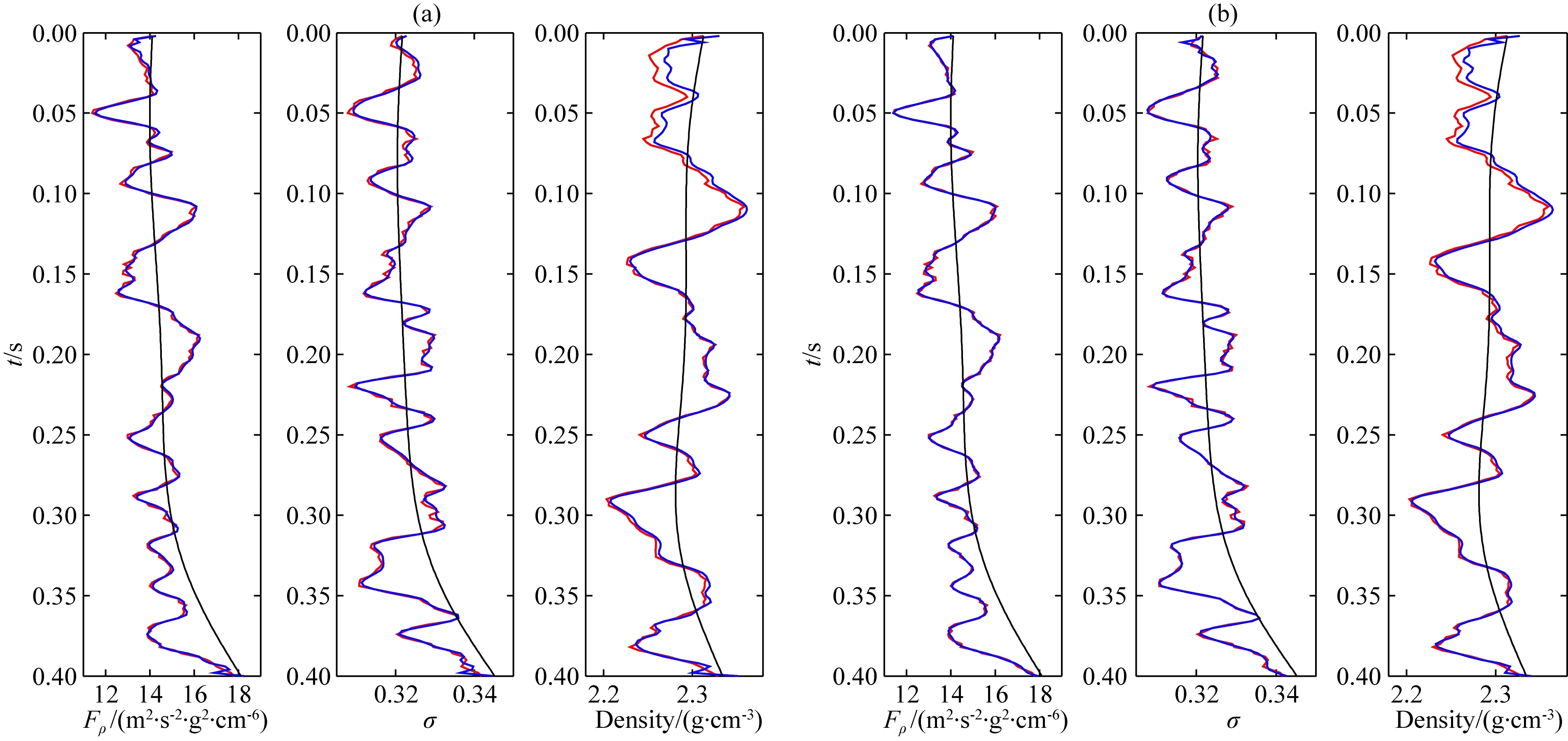
图5 新方法的反演结果
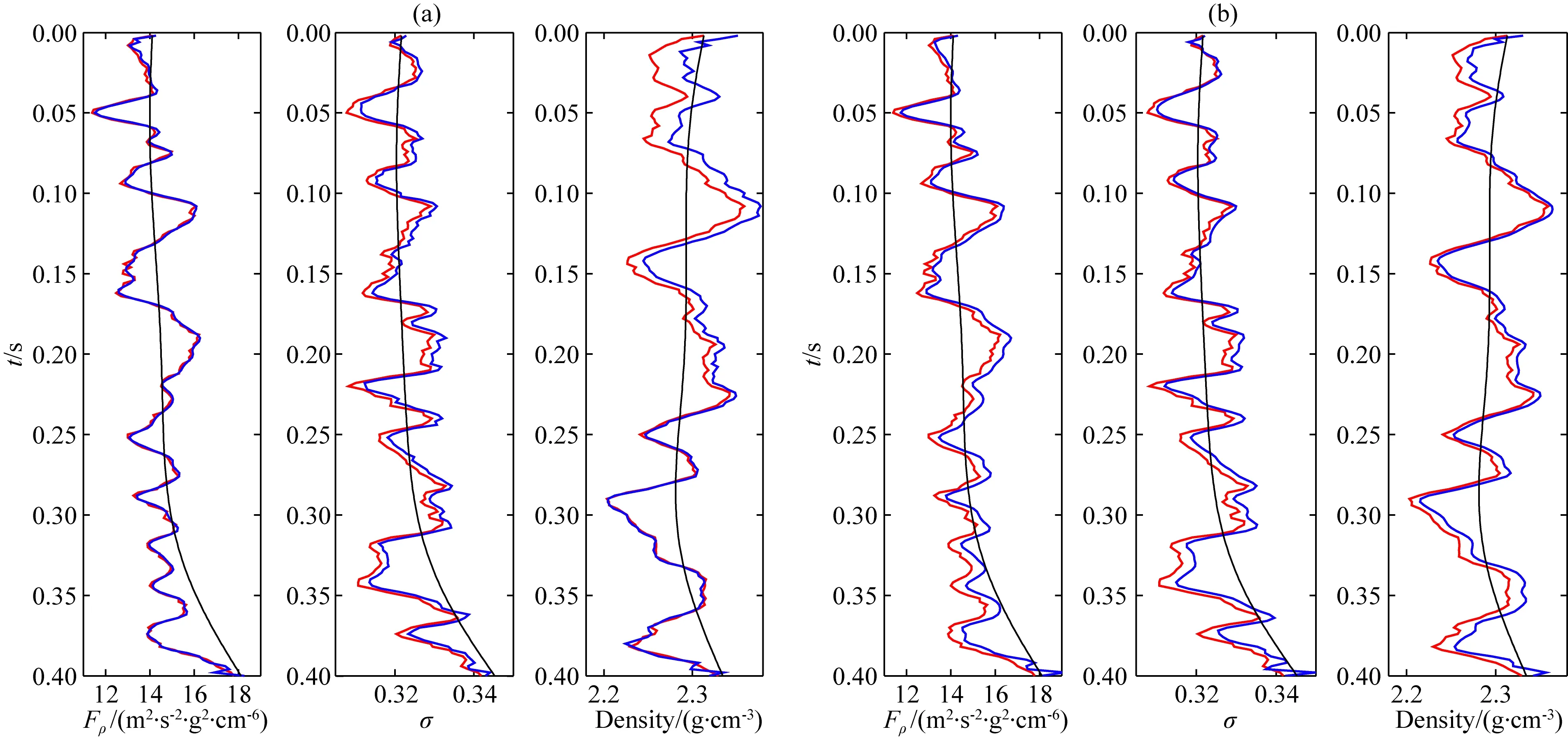
图6 基于传统近似公式的常规方法的反演结果
为了测试新方法的稳定性和抗噪性,利用图4b所示信噪比为0.5的合成数据对研究算法进行测试.图7a、b分别为含噪数据PP波单独反演和PP-PS波联合反演的结果,可以看出,即使在信噪比为0.5的情况下,新方法仍然能够稳定合理地估计出流体因子和泊松比,说明新方法具有良好的稳定性和抗噪性,同时也很好地验证了前述关于新方程反演稳定性分析的结论.
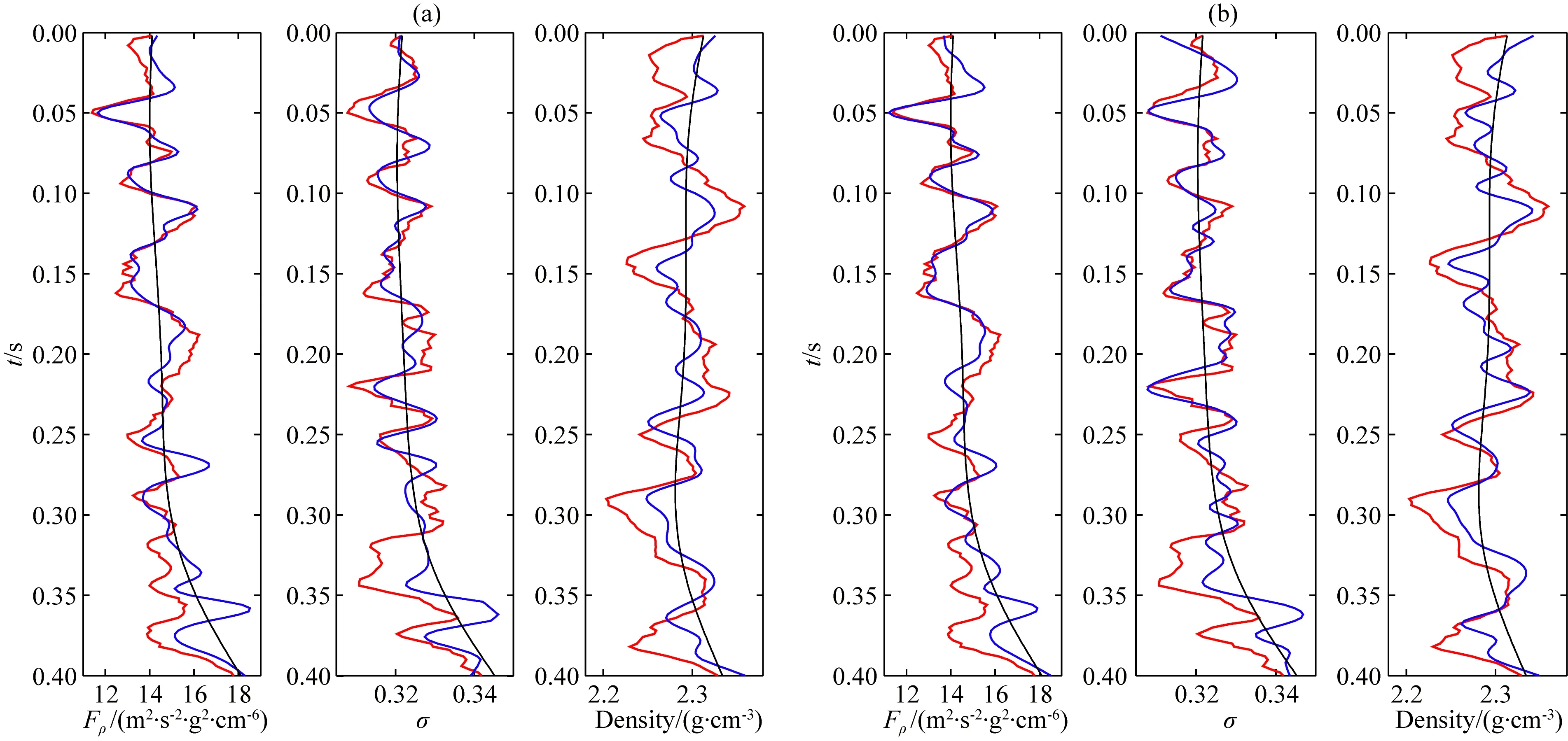
图7 新方法的反演结果(S/N=0.5)
3 实际数据测试
实际资料来自中国东部某勘探工区,图8为测试区域的叠加剖面.该区域实际采集的角道集数据角度范围为3°到45°(间隔1°),并已经过一系列常规处理满足叠前AVA反演的要求.图8中黑线标示位置为井A所在位置,图9为井A对应的真实测井曲线.图10为图9所示测井数据中流体因子Fρ与泊松比σ曲线交会图,从该图可以看出,流体因子Fρ和泊松比σ交会能够清楚地区分储层和非储层区域.
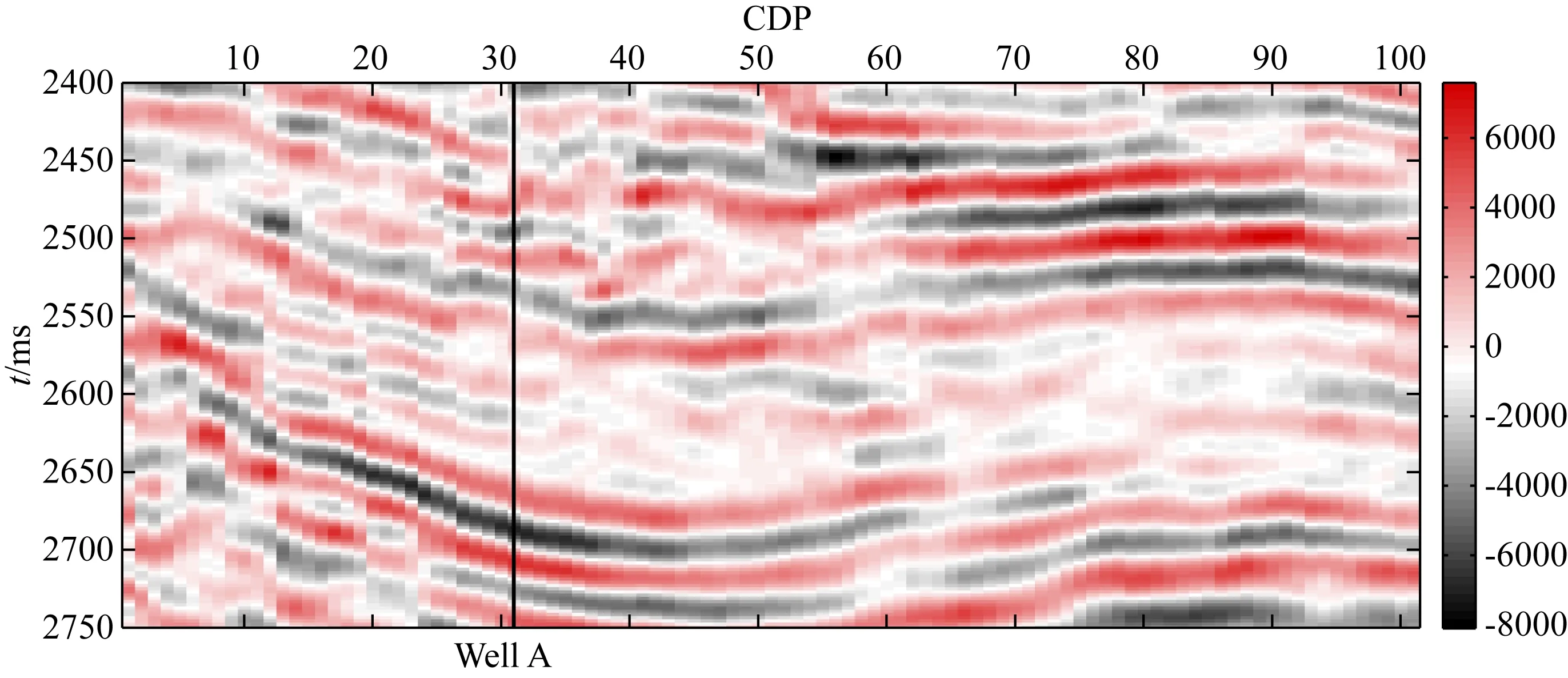
图8 测试区域的叠加剖面
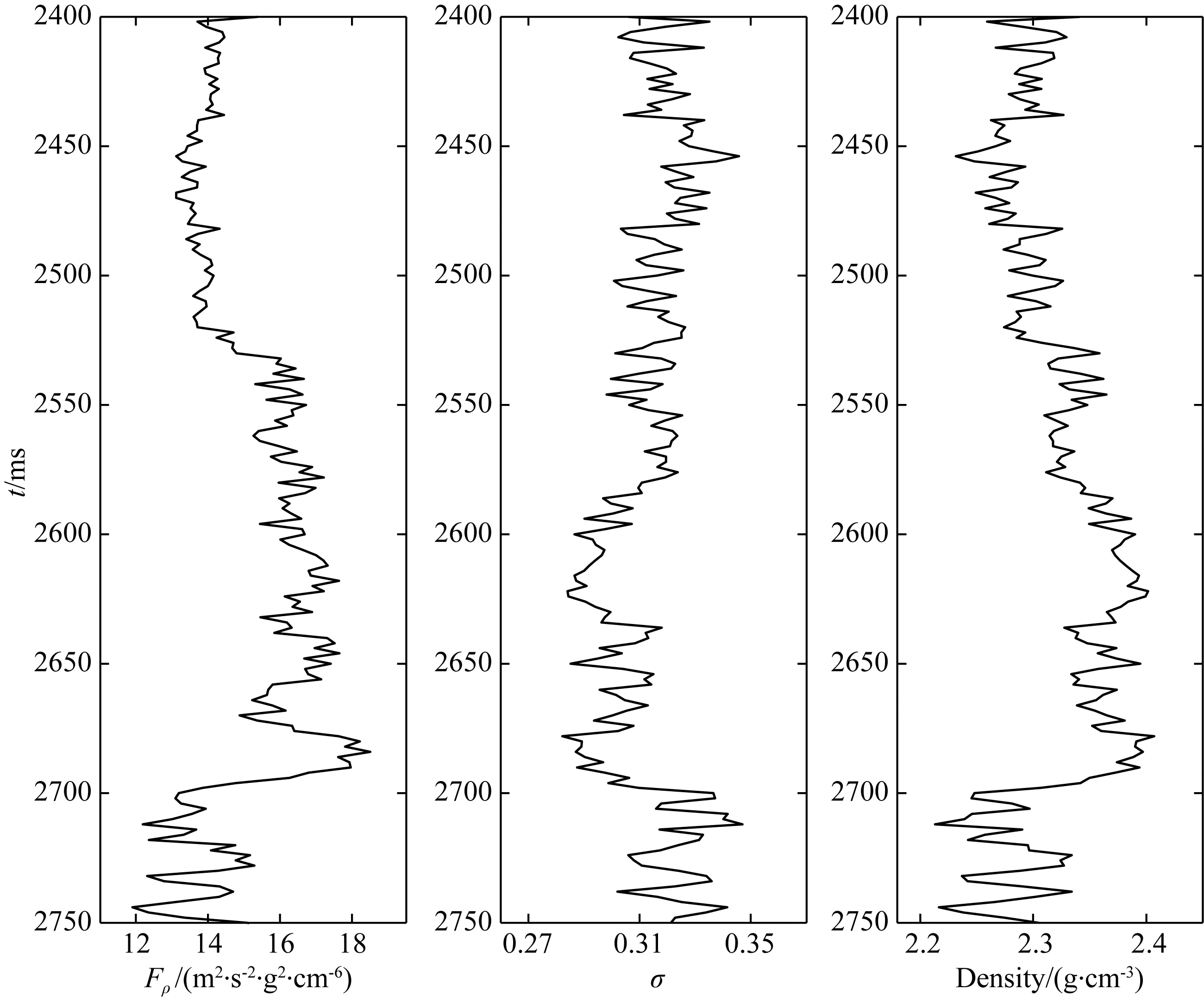
图9 井A的真实测井曲线
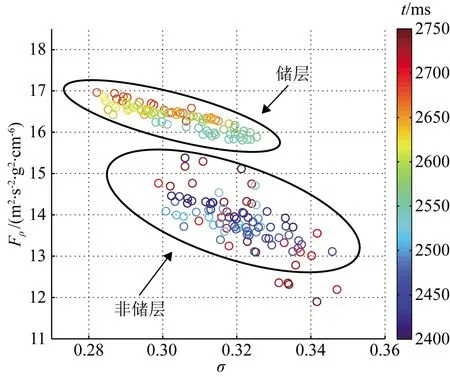
图10 图9所示流体因子和泊松比曲线交会图
由于工区实际数据的限制,仅有PP波数据参与反演.图11是利用新方法反演得到的流体因子(图11a)、泊松比(图11b)和密度(图11c)剖面.图12是利用基于传统近似公式的常规方法反演得到的流体因子(图12a)、泊松比(图12b)和密度(图12c)剖面.通过对比可以看出,新方法的反演结果在垂向分辨率和横向连续性方面均明显优于常规方法.为了进一步展示新方法的优势,图13给出了井A位置对应的井旁道反演结果,图中红线代表真实测井曲线,蓝线代表新方法反演结果,黑色实线代表常规方法反演结果,黑色虚线代表初始模型.通过对比可以看出,新方法流体因子、泊松比反演结果的精度明显高于常规方法,充分体现了本文方法的优势.
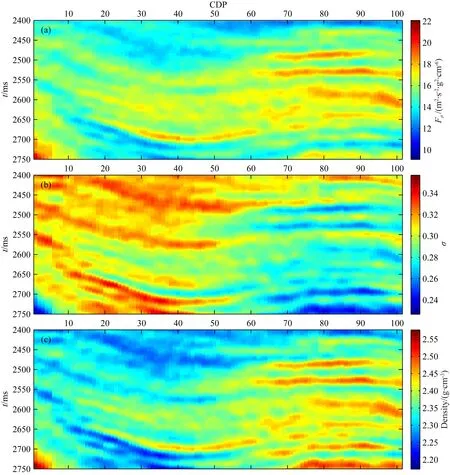
图12 基于传统近似公式的常规方法反演结果剖面
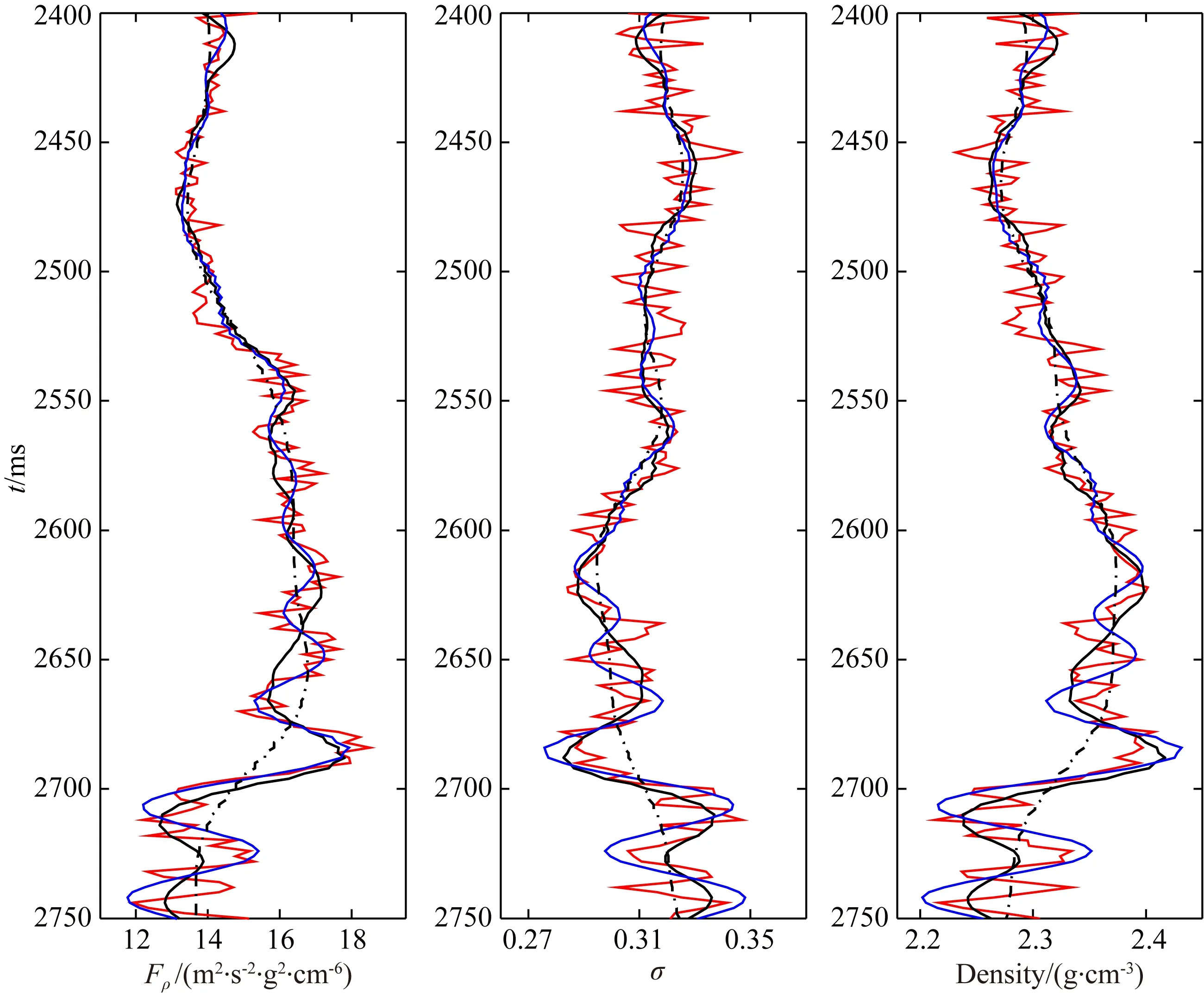
图13 井旁道反演结果对比
从图11a所示新方法流体因子反演结果可以看出,区域1和2均显示明显的流体因子高值,同时,从图11b所示泊松比反演结果可以看出,区域1和2均显示明显的低泊松比值,根据图10所示的交会结果很容易判定区域1和区域2位有明显的含油气性显示.此外,从图11a还可以看出,区域3所示流体因子反演结果虽然呈现高值,但明显比区域1和2所示流体因子值要低,此时如果仅仅依靠流体因子反演结果很难判定区域3是否为有效储层.但从图11b可以看出,区域3所示泊松比值呈现异常低值.大量研究表明,含气砂岩的泊松比值呈现异常低值,那么我们很容易判定该区域可能是含气储层,这也很好解释了为什么该区域的流体因子呈现高值但却远低于区域1和2.基于上述分析,我们可以推测区域1和2 为含油储层,区域3为含气储层,该分析结果与工区实际钻遇结果一致,充分验证了本文研究方法的可行性和有效性,对丰富储层含油气性高精度预测理论与方法具有十分重要的意义.
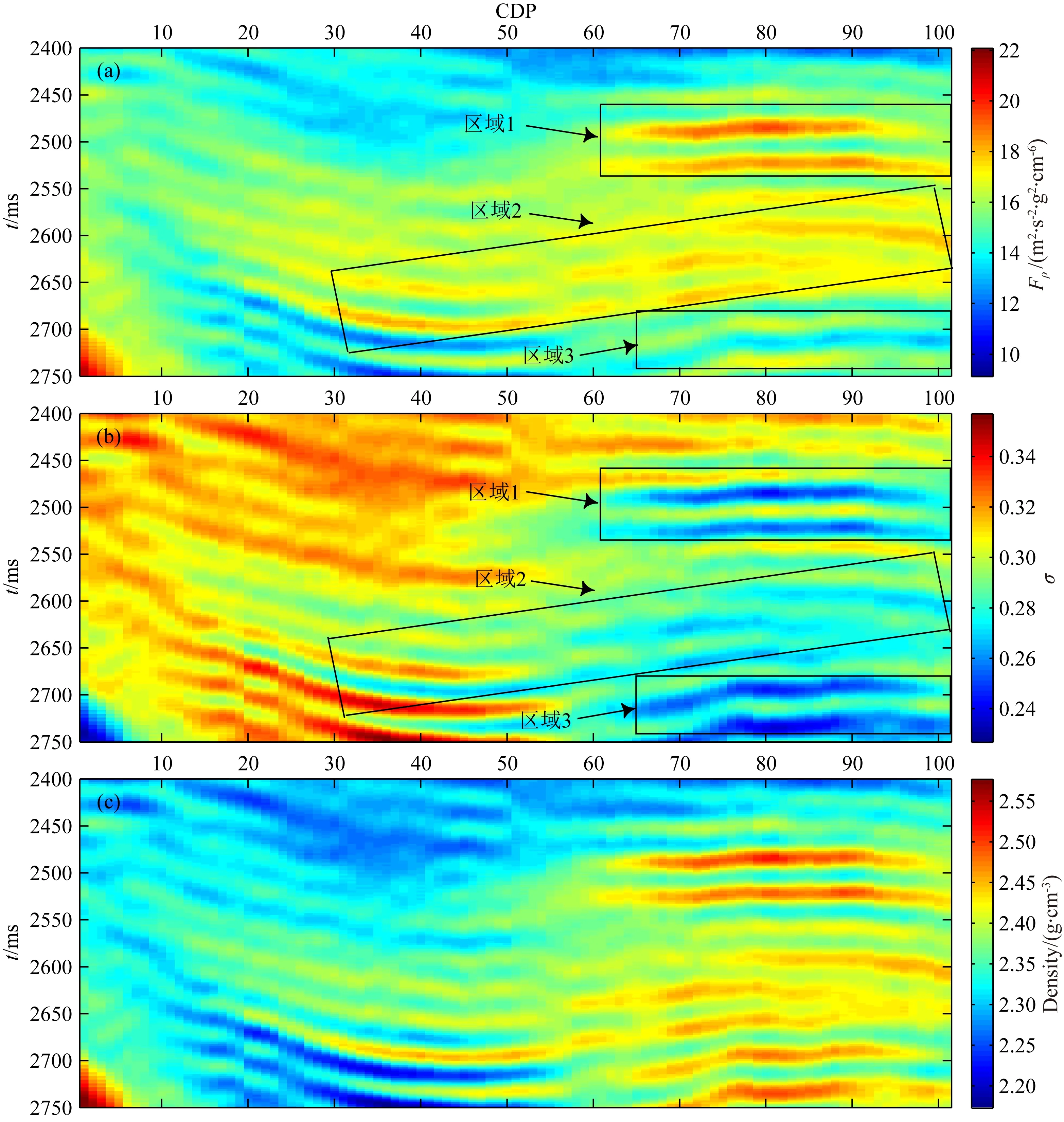
图11 新方法反演结果剖面
4 结论
本文首先通过流体因子敏感性分析优选出合适的流体因子,然后将传统形式的精确Zoeppritz方程改写为包含流体因子、泊松比和密度的新形式,并最终实现了基于新公式的贝叶斯非线性反演,有效地克服了传统近似公式固有缺陷对流体因子和泊松比反演结果精度的限制.同时,为了进一步提升反演结果对储层边界的刻画能力,有针对性地引入了服从微分拉普拉斯分布的块约束项.合成数据测试结果表明,新方法能够稳定合理地反演得到流体因子和泊松比且反演精度与PS转换波信息的利用均比常规方法表现得更好.二维实际数据测试结果表明,新方法反演结果的精度、垂向分辨率以及横向连续性均明显优常规方法,并且,同时利用流体因子和泊松比反演结果对研究区域的含油气性进行预测,能够有效降低预测结果的不确定性,充分验证了本文提出的基于精确Zoeppritz方程的储层含油气性预测方法的可行性和有效性.
本文选择的流体因子虽然很好地避免了干岩石纵横波速度比对Russell流体因子和流体体积模量流体识别能力的影响,但该流体物理意义并不明确,且在准确给出干岩石纵横波速度比情况下,其流体识别能力弱于Russell流体因子和流体体积模量.理论上,如果能够减弱或消除干岩石纵横波速度比对流体因子识别能力的影响,选择Russell流体因子或流体体积模量作为流体指示因子应该是最佳选择.因此,在本文研究内容的基础上,将随岩性或深度(走时)变化的干岩石纵横波速度比同时作为未知待反演参数,开展基于精确Zoeppritz方程的Russell流体因子或流体体积模量直接反演研究,达到消除干岩石纵横波速度比的影响并同时提升流体识别精度的目的,将是我们下一步计划研究的内容.但将干岩石纵横波速度比视为待反演参数或直接反演流体体积模量都将导致待反演参数数量增加,会严重影响非线性反演的稳定性同时降低反演结果的不确定性,这也将是我们后续研究中首要解决的难题.
致谢感谢所有合作作者在本文构思、研究及写作过程中的辛勤付出.感谢两位审稿专家对本文提出的宝贵建议.
附录A 包含流体因子Fρ、泊松比σ和密度ρ的线性近似公式推导
优选流体因子Fρ的表达为:
(A1)
泊松比的表达式为:
(A2)
根据多变量微积分链式法则可得:
(A3)
(A4)
将公式(A3)两边同时除以Fρ,将公式(A4)两边同时除以σ,则有:
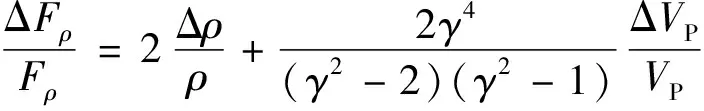
(A5)
(A6)
其中γ=(VP/VS)sat表示饱和岩石的纵横速度比.
将公式(A5)和(A6)联立求解可得:
(A7)
(A8)
将公式(A7)和(A8)代入Aki-Richards近似方程即可得到如下所示包含流体因子Fρ、泊松比σ和密度ρ的传统线性近似公式:
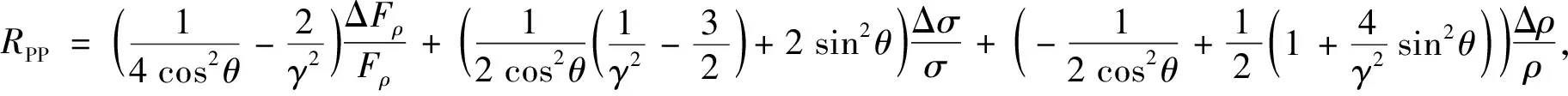
(A9)
(A10)
附录B 新形式精确Zoeppritz方程关于反射界面上下层流体因子Fρ、泊松比σ和密度ρ的一阶偏导数求解表达式
矩阵形式的新形式精确Zoeppritz方程表达式为:
AR=b,
(B1)
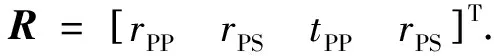
(B2)
其中m=(Fρ1,σ1,ρ1,Fρ2,σ2,ρ2).对式(B2)进行整理可得:
(B3)
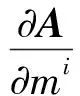
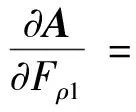
(B4)
(B5)
令M=η1/ξ1,N=ξ1/η1,则有:
(B6)
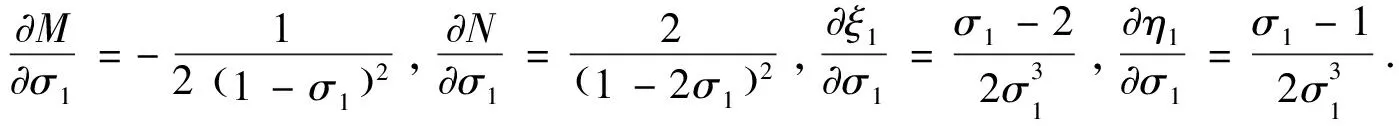
(B7)
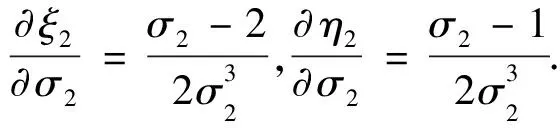
(B8)
(B9)
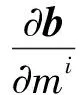
(B10)

