稳定正则化参数估计方法及其在盆地基底重力异常反演中的应用

刘燕东，纪晓琳，孟小红，王万银，王俊

1 中国地质大学(北京)地球物理与信息技术学院，北京 100083 2 长安大学地质工程与测绘学院, 西安 710054

0 引言

在位场处理和反演过程中，往往需要求解一个不适定问题.正则化方法实际上是不适定问题的正则化，也就是将不适定问题转换为一个适定问题.正则化参数的选取是否适当，不仅影响着算法的收敛性以及收敛速度，而且影响正则解是否收敛于问题的真实解.因此，正则化参数的选取对方程组求解结果至关重要，如何选取最优正则化参数一直以来都是正则化研究的难点和热点.

自Tikhonov(1963)提出求解不适定问题的正则化理论和方法以来，地球物理工作者将此方法应用到地球物理的各个领域.栾文贵(1988)在国内首次将正则化方法应用于地球物理反演.关于正则化参数的选取，国内外的许多学者提出了不同的方法，这些方法都是基于统计与数学概念.

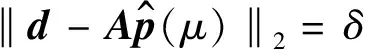
在数学方法中，使用最广泛的是L曲线法(Hansen, 1992).L曲线法通过解的向量模间接引入稳定性分析，应用很广泛(Calvetti et al., 2000; 马涛等, 2013).但解的范数与解的稳定性之间的定量关系不总是有效的.此外L曲线方法有多种局限性.Vogel(1996)指出L曲线法再一类特定问题中的收敛不足.Hanke(1996)指出，当信噪比在数据中趋于0时正则化参数不收敛于真解；且当精确解非常平滑时，L曲线方法具有局限性.最后，Xu等(2016)指出L曲线除“全局”角点外还存在一个角点.

综上，正则化参数的选择方法主要存在两个问题：(1)解的不稳定性的难以定义；(2)数据误差对正则化参数的灵敏度非常低.

Lima等(2019)提出的正则化参数的选择方法中，通过“交互”来选择正则化参数增加了很多工作量且存在很大的主观性.然而，不稳定性很大成分取决于研究人员的主观意向，所以定量表示解的不稳定性且能够直接利用其来直接选取正则化参数是重要的任务.

本文基于Tikhonov正则化方法，针对如何定量度量解的不稳定性以及如何产生这种定量度量，如何利用解的不稳定性定量度量来直接估计使解稳定的最优正则化参数展开研究.通过利用不同的随机噪声，将该方法应用到二维沉积盆地基底模拟重力数据与实测重力数据正则化反演中，证明这种方法在重力数据应用中的正确性和实用性.

1 稳定正则化参数估计方法

1.1 解的不稳定性定量度量

解的不稳定性定量度量ρ(μ)是在正则化参数取不同值时对于多组数据反演得到的多组解之间的向量差的无穷范数中的最大值.由于任意两个独立序列偶然产生两个与彼此非常接近的解的概率很小，故如果一组数据产生的解与其他数据的解相差太远，足以证明反演过程由于解的不稳定性而不适定.另一方面，5组数据也足以使概率值小于0.1%(Lima et al., 2019).在理想情况下，多组数据来自多次野外测量.

1.1.1J组数据来自J次野外测量

计算给定正则化参数值μk产生的解的不稳定性定量度量其求解步骤如下:

(1)J次野外测量得到的J组数据，表达式为

dj=d+rj,j=1,…,J,

(1)

其中d是一组无噪声的理论观测值，rj是伪随机时变噪声序列.

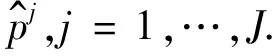
(3)计算J组估计解之间的差的绝对值，表达式为

i=j+1,…,J,l=1,…,M.

(2)

(4)计算标量ρji作为Δpji的无穷范数，即：

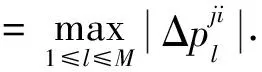
(3)

(5)当前正则化参数μk产生的解不稳定性定量度量，表达式为

(4)

将其作为解离差的度量.

1.1.2 从一次野外测量得到J组数据

用于反演的J组数据本应来自J次野外测量，但是，一般情况下的实际重力勘探只进行一次野外测量.通过对一次野外测量所获得的数据分别加入J组不同噪声也可得到的J组数据，下面从方差角度证明通过人为加入噪声获得的J组数据与J次测量获得的J组数据对于正则化反演是等价的.

一次野外测量中得到的一组数据是位置与时间的函数，由理论值do(ri),i=1,…,N与噪声ε1(ri,t)组成：

d1(ri,tj)=do(ri)+ε1(ri,tj),j=1，

(5)

构造随机变量α(ri,t)与ε(t)互相独立且方差相同或相近，那么数据加入J组噪声后的方差为

V(d1(ri,tj)+αJ(ri,tj))=V(do(ri))

+V(ε1(ri,tj))+V(αJ(ri,tj)),

(6)

由于do(ri)与ε1(ri,tj)是实数，方差为零，且：

V(αJ(ri,tj))≈V(ε(t)),

(7)

故得到：

V(d1(ri,tj)+αJ(ri,tj))≈V(ε(t))，

(8)

因为不稳定性的分析与正则化参数的估计主要取决于数据中的噪声方差，故式(8)表明，多次测量获得的J组数据，与用J组噪声分别扰动一次测量数据得到的J组数据是等价的.

1.2 确定使解稳定的正则化参数的最优值

根据解的不稳定性定量度量ρ(μ)的定义，可以利用ρ(μ)来确定正则化参数的最优值.定义解的不稳定性定量度量的变化量为

Δρk=ρk-1(μk-1)-ρk(μk),k=2,3,….

(9)

从理论上说，因为μ控制正则化的数量，所以可以预测ρ(μ)是单调递减的.也就是说，正则化参数μ越大，不稳定性越小.那么，当一个单位正则化数量时Δρk很小，可以认为μk是使解稳定的正则化参数：

(10)

在Δρk满足式(10)时，认为Δρk很小.其中，β为稳定系数，β根据求解精度来确定.若β取值过大，则解不稳定；若β取值过小，则解过稳定.

在实际情况中，可能会出现解的不稳定性定量度量偏离单调行为的情况，通常是由于计算不精密或违背重要的前提造成的.此时需要停止计算，检查并修改问题所在，重新开始.

2 二维沉积盆地重力异常正演

沉积盆地由上界面、沉积层与基底组成.假设沉积层的上界面是一个平面，在直角坐标系中，z轴向下为正.将沉积层剖分为M个二维矩形棱柱，模拟沉积盆地基底起伏.二维矩形柱体的宽度已知且为常数，厚度为参数pj，二维矩形柱体的顶面与沉积盆地的上界面重合，底面与沉积盆地的基底重合(如图1所示).

图1 二维沉积盆地模型示意图

M个二维并置矩形柱体在观测点处产生的重力异常可以近似表示沉积盆地基底起伏在观测点处引起的重力异常，即：

(11)

其中fi(p)表示第i个测点O(xi,zi)处的重力异常，第j个柱体的厚度为pj，Δg(xi,zi,pj)表示第j个柱体在第i个测点处引起的重力异常，其表达式为(Rao et al., 1994)：

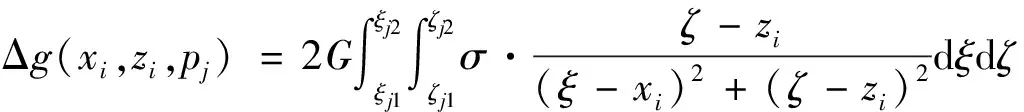
(12)

其中，G为牛顿万有引力常数；σ为沉积层与基底之间的密度差，为常数；(ξ,ζ)为二维矩形柱体内微元的坐标，如图2所示第j个柱体的坐标范围为ξj1～ξj2，ζj1～ζj2；柱体厚度参数pj=ζj2-ζj1；柱体水平宽度dx=ξj2-ξj1.

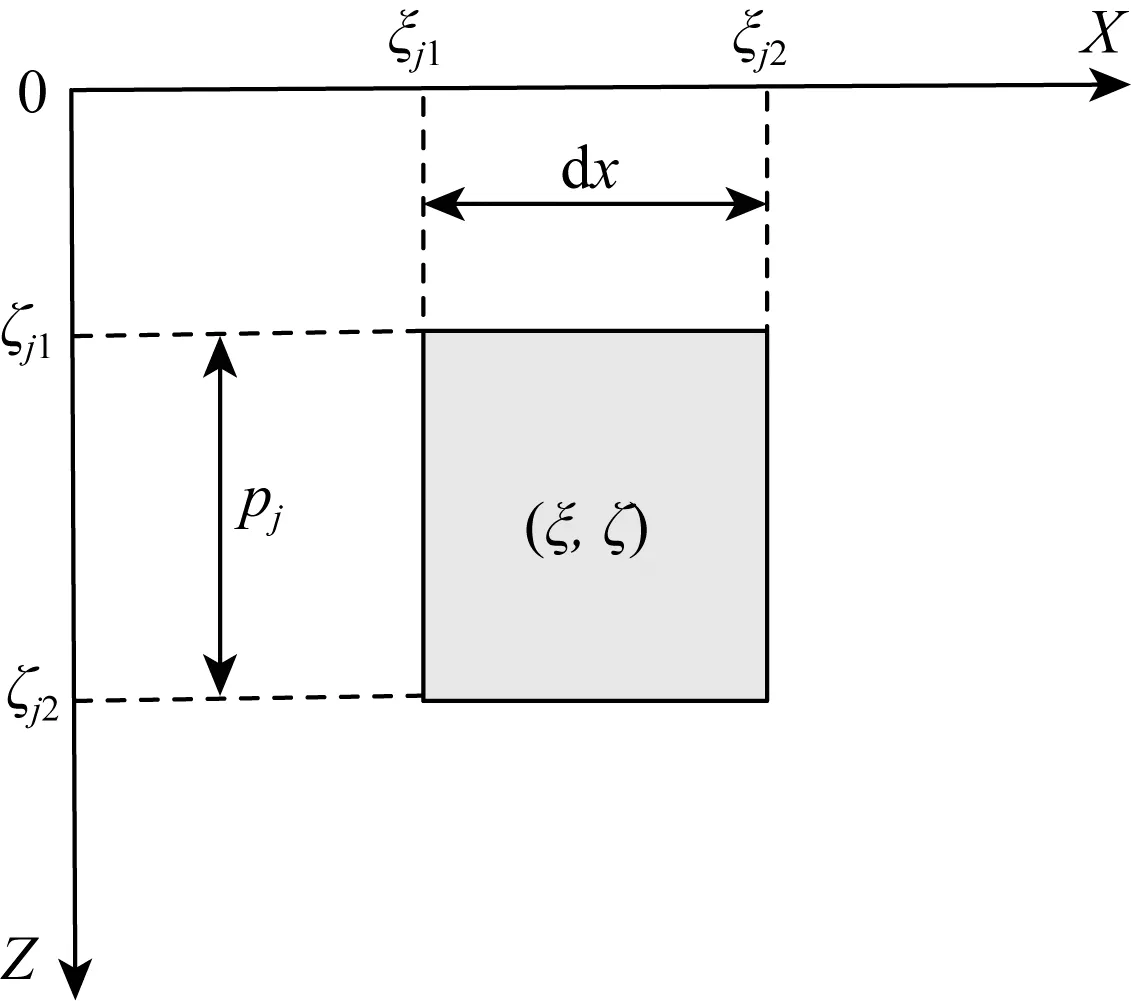
图2 二维矩形柱体微元示意图

在模型测试中，假设重力异常的观测面位于z=0的平面上，且与沉积层上界面重合，则式(12)可以化简为

(13)

3 二维沉积盆地基底正则化反演

3.1 目标函数

基于Tikhonov正则化方法来构造正则化反演的目标函数，计算使得目标函数极小的模型参数p，目标函数为

(14)

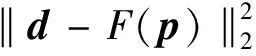
φ(p)=(p-p0)TLTL(p-p0)，

(15)

其中p0为先验信息，可以用已知的深度信息或前一次反演的结果；L为光滑度矩阵.

3.2 高斯牛顿法求解

式(14)构造的目标函数ψ(p)的一阶导数(即梯度)用g(p)表示；目标函数的二阶导数(即Hessian矩阵)用H(p)表示.假设当前的模型向量为pk，那么梯度矩阵与Hessian矩阵的表达式为

(16)

(17)

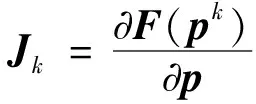
将目标函数ψ(p)在pk附近进行Taylor级数展开，并且忽略二次以上的高阶项，得到：

ψ(p)≈ψ(pk)+[g(pk)]T(p-pk)

(18)

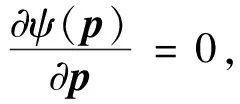
H(pk)·δpk=-g(pk).

(19)

用奇异值分解法求解线性方程(19)得到模型修正量δpk，模型参数的迭代公式可表示为

pk+1=pk+δpk，k=0,1,…，

(20)

4 模型测试

通过将这种稳定的方法应用到模拟二维沉积盆地重力数据的盆地基底正则化反演中，测试该方法在通过对一次野外测量所获得的数据分别加入J组不同噪声得到的J组数据与从J次野外测量中得到J组数据这两种情况中的反演效果.

4.1 模型设置

本次模型测试设计的二维模拟沉积盆地的基底起伏如图3所示，其中沉积物和基底之间的密度差为-0.3 g·cm-3.

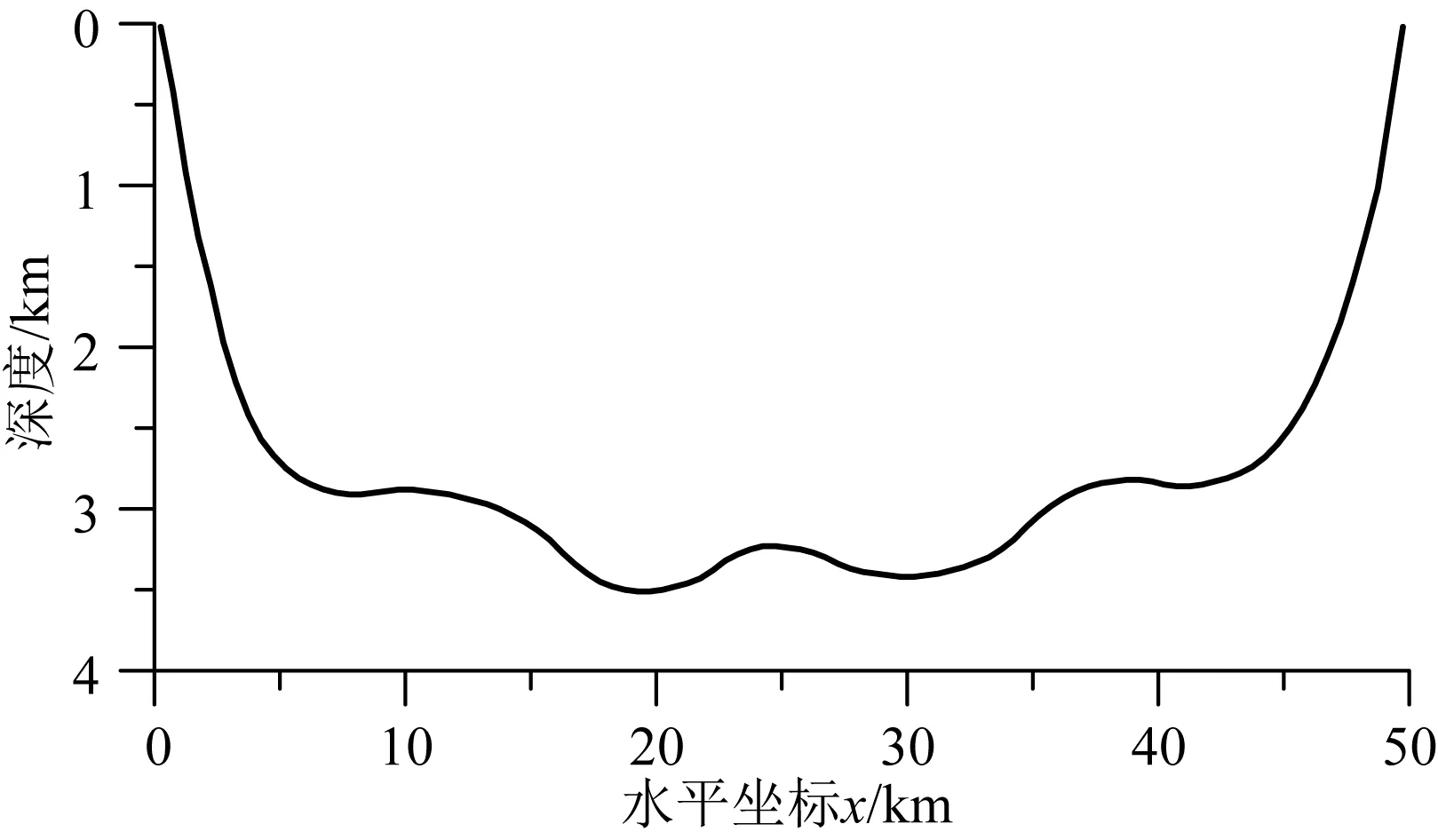
图3 二维模拟沉积盆地的基底起伏

正演二维模拟沉积盆地的基底起伏产生的重力异常时，进行100个点的模拟观测，观测点间隔为0.5 km.将二维沉积盆地剖分为100个宽度为0.5 km的二维矩形棱柱，且棱柱中心的x坐标与每一个观测值的x坐标一致.正演得到理论重力异常值(图4a)与含噪声的重力异常(图4b).给定3个点的水平坐标与已知深度，作为二维沉积盆地基底深度正则化反演的先验信息(表1).

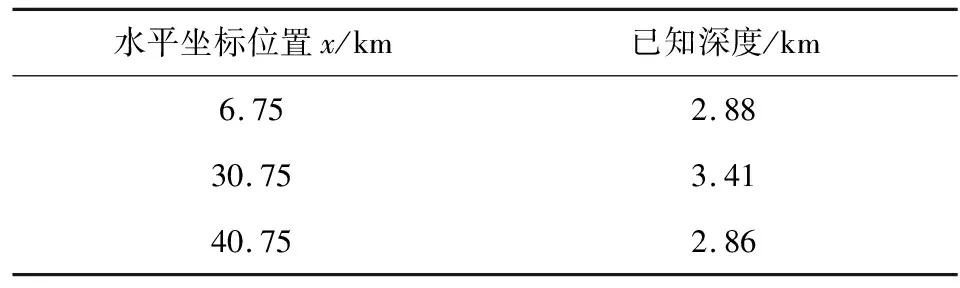
表1 反演二维模拟沉积盆地基底深度时的先验信息

4.2 一次野外测量

为了模拟实测数据的情况，对于已用单个单高斯伪随机噪声序列ε1(ri,t)(i=1,…,100，均值为零，标准差为0.1 mGal)扰动图4a的重力理论观测值得到含噪声的模拟实测重力观测值如图4b所示.为了说明变量α(ri,t)的噪声分布类型可能不同于ε1(ri,t)的分布，用25组不同的均匀随机噪声α25(ri,tj)(对于i=1,…,100，平均值为零并且均方差为0.1 mGal)扰动一组模拟实测观测值(图4b)，模拟从一组勘探数据获得J组数据的情况.

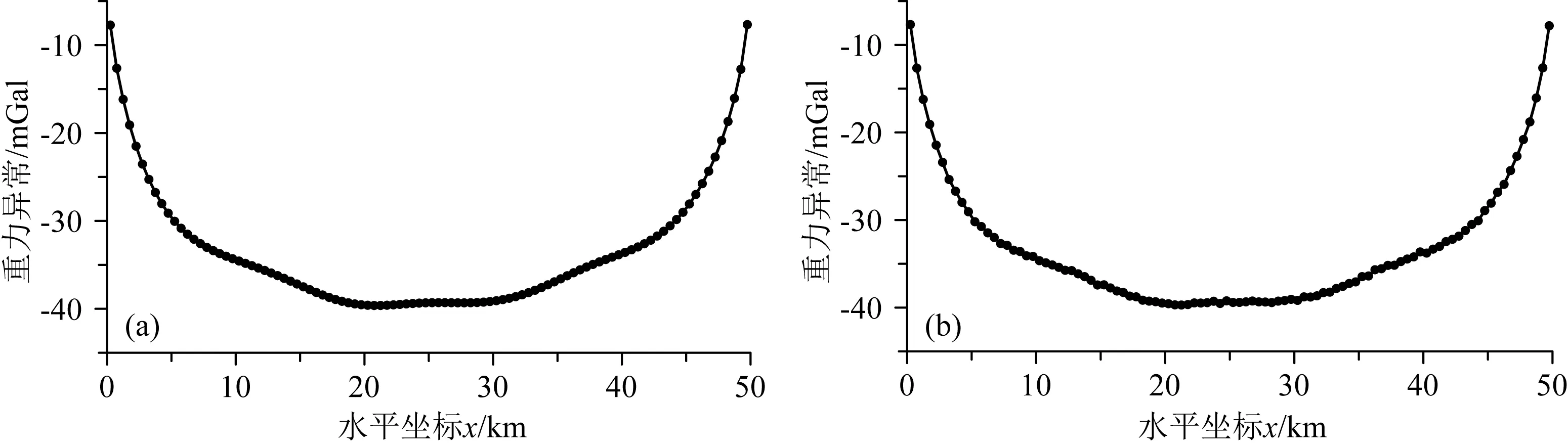
图4 沉积盆地基底起伏正演重力异常图

用高斯牛顿法反演这25组数据.图5a中实线为25组反演解的不稳定性度量ρ随正则化参数μ的变化曲线，以左轴为单位；虚线为数据均方误差RMS随μ的变化曲线，以右轴为单位；图5b为单位正则化数量产生的解不稳定性定量度量的变化量Δρk/Δμ随正则化参数μ的变化曲线.根据Δρk/Δμ(稳定系数β取0.005)，直接选取到的正则化参数的最优值为μ*=8.而在图5a数据误差均方根曲线中，正则化参数μ从0.01变化到15，而均方误差RMS仅从0.1497变化到0.1626，由此可见数据误差对正则化参数的灵敏度非常低.图6为正则化参数μ=0.01、0.5、2、8时的25组反演解，μ=0.01时反演解极不稳定，μ=0.5、2时反演解较为不稳定，μ=8时反演解较稳定.且μ=8时，均方根误差为0.1592 mGal，在可接受误差范围内.故正则化参数的最优估计μ*=8是同时产生稳定的解和可接受的误差的最小的正则化参数.

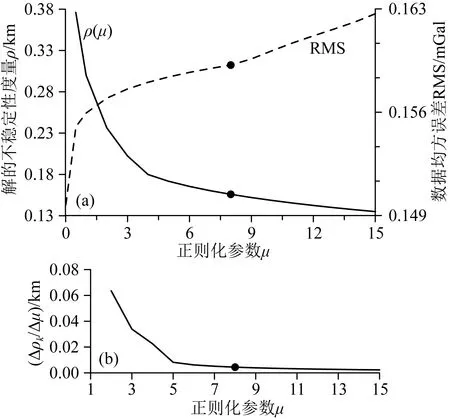
图5 (a)不稳定性曲线和数据误差均方根曲线；(b)Δρk/Δμ曲线

4.3 J次野外测量

用25组高斯噪声(均值为零，标准差为0.1 mGal)扰动理论重力异常(图4a)，模拟从J次野外测量获得J组数据，以证明上述模拟实测数据情况的合理性.反演这25组数据，根据单位正则化数量产生的解不稳定性定量度量的变化量Δρk/Δμ(稳定系数β取0.005)，直接选取到的正则化参数的最优值为μ*=8.

反演结果图7与图6对比，可说明模拟从一组勘探数据获得J组数据所得到的解与模拟的J次野外测量所得的解非常接近.且在该种情况下，利用稳定正则化参数估计方法确定的最优正则化参数同样是μ*=8.故本文的方法适用于一般情况下只进行一次野外测量的实际重力勘探情况.

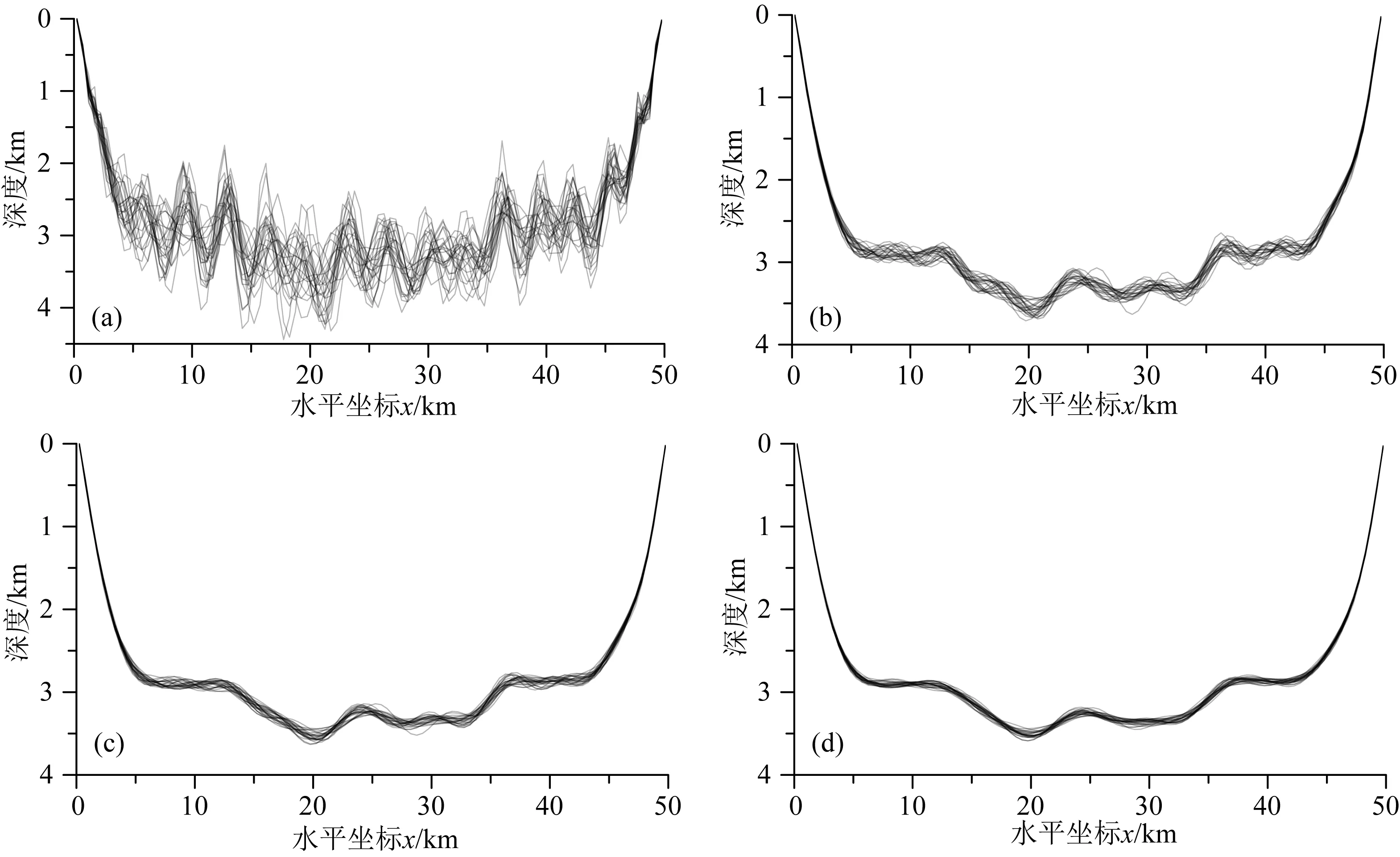
图6 模拟实测数据的25组扰动重力解

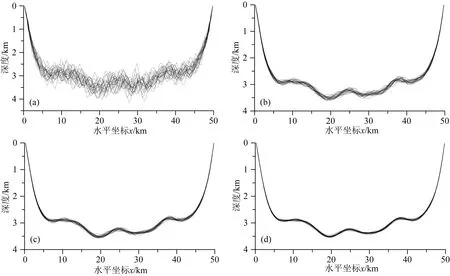
图7 25组扰动重力解

5 实际资料测试

5.1 区域地质特征

为了检验稳定正则化参数估计方法在二维沉积盆地实测重力数据正则化反演中的应用效果，选择非洲西海岸的加蓬盆地的部分卫星测高重力异常数据进行了实际资料测试.

本次研究区位于非洲西海岸加蓬盆地，加蓬盆地是西非海岸盆地群中的一个富油气盆地(刘深艳等, 2011).加蓬盆地由3个二级构造单元组成(图8)，以恩科米转换断层、兰巴雷内高地为界分为南加蓬次盆、北加蓬次盆和内次盆(赵红岩等, 2017).收集到的SW-NE走向的剖面CD的剖面位置如图8所示，地质构造资料如图9所示.本次研究北加蓬次盆中的剖面AB.

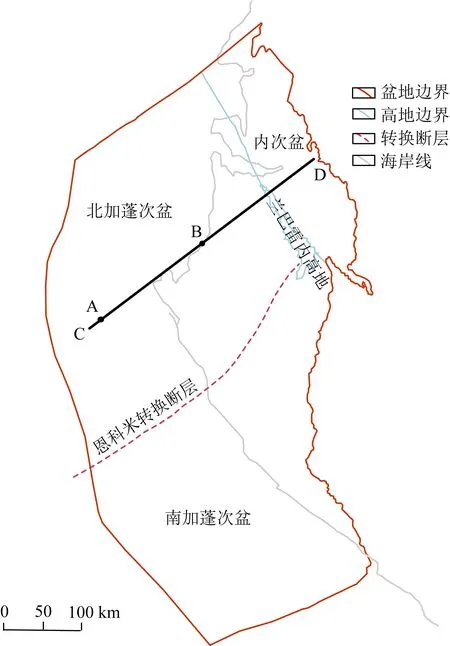
图8 加蓬盆地构造划分与剖面位置示意图(据赵红岩等，2017)

北加蓬次盆(North Gabon sub-Basin)沉积组合具有明显的三分性，发育了盐下、盐层及盐上三套沉积层序，含油气层序以盐上层系为主(郭念发, 2015).故北加蓬次盆具有十分重要的研究意义.北加蓬次盆从西向东构造单元划分为外裂谷盆地、中央隆起带与内裂谷盆地，共三个构造单元(图9)(刘亚雷 等, 2019).

5.2 反演数据准备

位于北加蓬次盆SW-NE走向的测线AB的布格重力异常如图10a所示，其包含了盐下、盐层及盐上3套沉积层序与基底产生的重力异常，故采用最小曲率法(纪晓琳等, 2015)对布格重力异常进行位场分离后得到反映盆地基底的剩余布格重力异常(图10b)作为基底起伏反演的基础数据.由于北加蓬次盆发育多套沉积层序且含油气，且本次测试的主要目的是用实测数据证明稳定正则化参数估计方法的可靠性与实用性，故将盆地的构造简化进行反演.根据查得的密度资料(纪晓琳等, 2019)(如表2)，取沉积层密度为3套沉积层的平均密度2.35 g·cm-3，盆地基底密度为2.8 g·cm-3，所以本次实际资料处理所取的沉积层与基底的剩余密度为-0.45 g·cm-3.根据北加蓬次盆的剖面CD的地质构造信息(图9)，给出用于正则化反演的先验信息(位置及深度)如表3所示.

表2 密度资料(单位：g·cm-3)(据纪晓琳等, 2019)

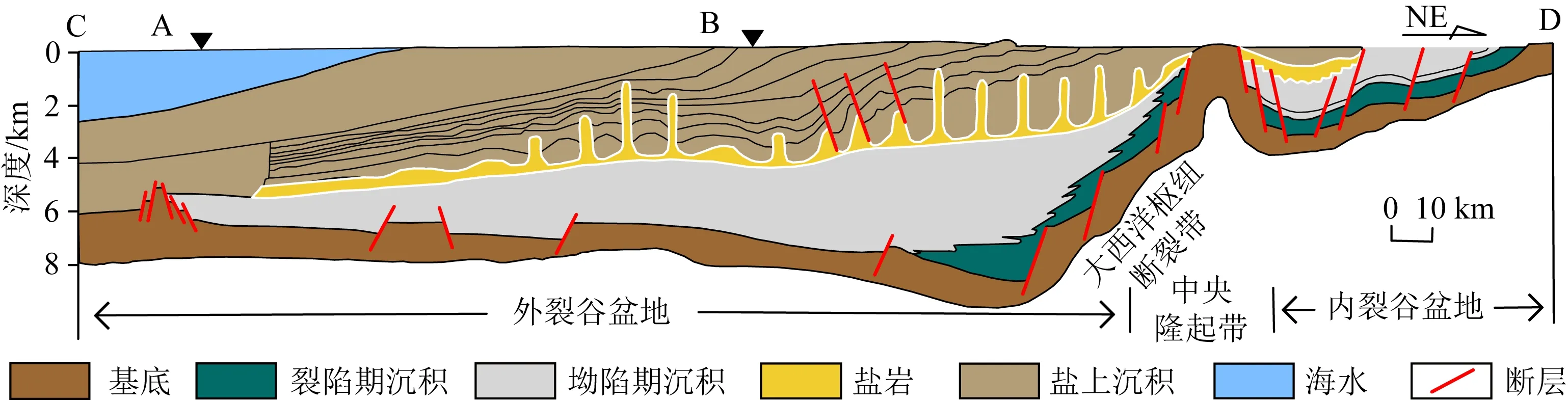
图9 北加蓬次盆CD剖面构造划分(据刘亚雷等，2019)

表3 正则化反演的深度先验信息

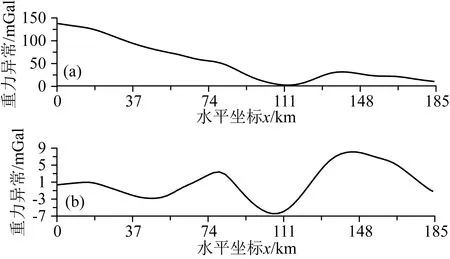
图10 (a)测线布格重力异常；(b)剩余布格重力异常

5.3 实际资料反演结果

利用5.2节中为正则化反演所准备的数据，用稳定正则化参数估计方法在正则化反演中选择最优正则化参数得到最优的反演结果.解的不稳性定量度量随正则化参数的变化曲线如图11a所示，根据产生的Δρk/Δμ(稳定系数β取0.005)(图11b)，直接选取的最优正则化参数为μ*=13.最优反演结果如图12b所示，反演的15组解稳定性较好，解不稳定性定量度量为0.1786.

图11 (a)解不稳定定量度量随正则化参数单调递减；(b)Δρk/Δμ曲线

盆地基底反演结果的深度范围在6.0～7.4 km，反演结果与测线对应的地质构造基底深度基本吻合，基底整体起伏特征基本与地质剖面中基底特征一致，且反演的15组结果稳定性较好(如图12所示).说明稳定正则化参数估计方法在实际数据中确定的最优正则化参数可以得到稳定最优的反演解.

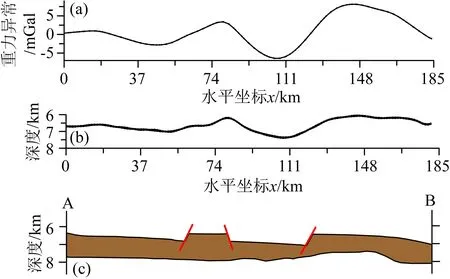
图12 北加蓬次盆AB剖面基底反演结果与地质剖面对比图

6 结论

(1)通过对一次野外测量数据加入不同噪声得到的J组数据与从J次野外测量中得到的J组数据这两种情况的模型测试结果表明，在这两种情况下利用稳定正则化参数估计方法直接确定的最优正则化参数一致，且获得的反演解非常接近，都能够反演得到较为准确的模型基底深度.故该方法适用于一般情况下只进行一次野外测量的实际重力勘探.

(2)将稳定正则化参数估计方法应用到北加蓬次盆剩余布格重力异常中进行盆地基底反演，最优反演结果是稳定的且符合当地地质构造认识，基底整体深度与起伏特征基本与地质剖面中基底特征一致.故在实测重力数据中，稳定正则化参数估计方法也可以直接确定最优正则化参数以得到稳定最优反演解.

(3)应用稳定正则化参数估计方法所需的前提条件非常少，且与随机噪声分布无关，故该方法具有广泛的适用性.

致谢感谢评审专家提出的修改意见.