基于机器视觉的瓜科砧木苗参数提取①

周 磊 龚征绛 费焕强 陈 武 查 杨 喻擎苍

（浙江理工大学 浙江杭州 310018）

嫁接机种类主要有全自动嫁接机、半自动嫁接机及手动嫁接机。全自动嫁接机价格贵，难以推广，而半自动和手动嫁接机自动化程度较低，生产效率低下［1］。由于幼苗茎部较为脆弱，容易造成幼苗茎断［2］，因此，可利用机器视觉技术，识别砧木苗状态，利用机器手从幼苗上方抓取幼苗的茎部［3］，实现自动取苗，提高嫁接机器人的嫁接速度和成功率。

1 视觉处理模块

视觉处理模块由光源、摄像头，树莓派3B 开发板等组成，见图1。摄像头安装在装置上方，考虑焦距6 mm、选择视场角60.6°、500 万像素的排线摄像头。

图1 取苗装置

2 参数提取

2.1 参数提取流程

瓜科砧木苗的参数提取主要包含以下流程：通过摄像头实时采集图像，根据颜色空间选取对图像进行多值化操作，将相同色彩参数的像素点连接起来形成连通域，根据连通域的内外连接确定连通域间的关系，将图像中较小连通域去除，即图像去噪，提取连通域最外层，形成轮廓链，根据轮廓链点集计算最小外接圆，确定子叶的张开角度，计算特征参数（图2）。

图2 参数提取流程图

2.2 颜色空间转换与目标像素提取

颜色空间的选取决定了多值化后图像中像素点代表数值，因此，选择合适的颜色空间尤为重要，通过树莓派采集的图像如图3所示，可以看出两图片叶片亮度不一样。因RGB 颜色空间不能反映颜色的具体信息，HSV 空间能够直观反映明暗、色调以及鲜艳程度，因此，选用HSV 颜色空间［4］。

图3 采集的图像

RGB与HSV颜色空间可通过公式进行转换：

利用滴管工具对图3具有代表性的像素点进行提取，利用转换公式得到HSV 范围，如表1 所示。结合表1与连通域形成区域的分析，提取叶面（边缘）、叶面（内部）、茎、茎白（内部）、茎白（边缘） 数据，可知 H 值为 76°～145°，S值为 0.24～0.38，V为0.69～1.00的图像处理结果最优。对采集到的图像利用参数区间处理，并与RGB 空间下对比，结果如图4 所示，其中左侧在RGB 空间下，右侧在HSV 颜色空间下。可以看出参数细化后，HSV空间得到的轮廓链较RGB空间下更完整，轮廓链更平滑，凸点更少［5］。

图4 RGB与HSV颜色空间下图像处理对照图

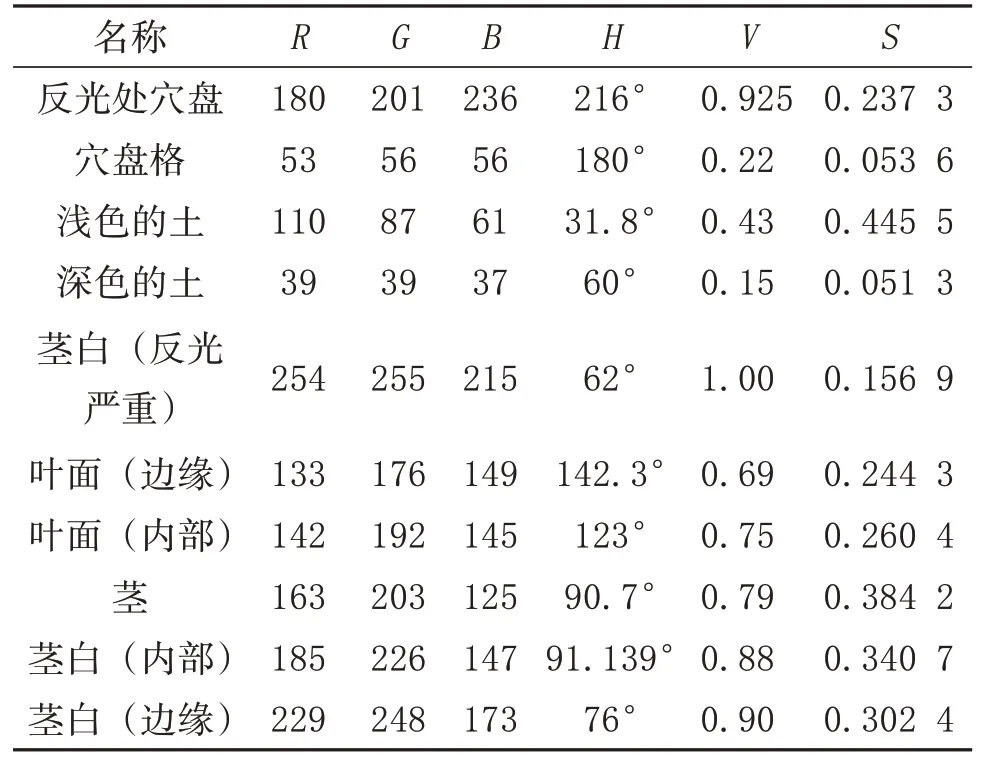
表1 像素点颜色空间转化

2.3 最小外接圆算法的优化

子叶张开角度是通过砧木苗两片子叶端点计算得到［7］，采用最小外接圆法可以得到砧木苗端点信息，使用opencv 中自带的minEnclosingCircle法得到如图5 所示结果。根据图5 计算得到最小外接圆算法的平均耗时为92.5 ms。由于传统最小外接圆算法使用的是四点确定一个圆的算法，该法虽然保险，但是运算量过大，存在优化空间。因此，本研究提出两点确定最小外接圆方法［8］。

图5 传统最小外接圆算法处理结果图

根据数学定理可知，两个点若想确定一个圆，则一个点必须是圆心，另一个点与该点的距离是半径。本研究两点确定圆本质上是找到轮廓链中距离最长的两点即直径，两点的中心为圆心，两点距离的一半是半径［9］。因此，本方法在数学意义上是可行的，流程图如图6所示：

图6 两点确定最小外接圆算法流程图

为检验优化后最小外接圆算法与传统方法时间效能及准确性，分别从处理时间及2方法求端点进行比较，图7 为处理时间的比较。由图7 可看出，优化后最小外接圆算法耗时最多为13 ms，最少为9 ms，平均处理时间为11.3 ms，处理时间较为稳定，而传统最小外接圆算法耗时最多为112 ms，最少为59 ms，平均处理时间为77.6 ms，波动较大。

图7 优化算法与传统方法的处理时间比较

观察图7 中6 组实验，第三幅图的处理时间发生了突增，可以推断轮廓链点集大小是影响传统最小外接圆算法效率的一个因素［10］。因此，使用Opencv自带的resize函数，对同一张砧木苗图像放大，并分别使用传统最小外接圆算法与优化最小外接圆算法处理，结果如图8所示。

图8 大数量点集两者比较

当轮廓链点集有732个点时，两算法处理时间差距比较明显，分别为51、8 ms，并随着点集的不断增加，差距越来越大，本研究最大点集数为233 8，优化算法处理时间为22 ms，而传统算法时间为167 ms。因此，传统外接圆算法的处理速度明显慢于优化外接圆算法。

比较传统方法对应的端点以及优化算法计算出的端点，传统方法可以得到圆心，遍历轮廓链中的点集，使得某两点的坐标满足：(x-a)2+(y-b)2=r2，x∈ [0，639]，y∈ [0，479]，而优化的算法可以直接得出端点信息，如表2所示：

表2 两个算法取得的端点值误差

2.4 子叶张开角度提取

运用优化外接圆算法，得到了左右端点A、B为 (xA，yA)、(xB，yB)，如图 9 所示。AB 线段的斜率可以表示为：利用反三角函数，求出子叶的在该坐标系下的张开角度：θAB=arctan(kAB)。

图9 砧木苗坐标示意图

2.5 最长接线宽度

根据子叶张开角度，提取子叶的最长截线宽度，如图10所示。

图10 垂直法求解最长截线宽度图

从大于A 的纵坐标开始遍历轮廓，求取任意一点与A 点关于x 轴的夹角，以C 点作为假设点开始计算。计算A 点与C 点间的欧式距离，记为ρ：通过反三角函数得出A 点与C 点关于x 轴方向的夹角，记为θ1：θ1=A点与B点关于x轴方向的夹角，即 子 叶 的 张 开 角 度 ， 记 为θ2：θ2=h=sin(θ-θ)*ρ。将轮廓链上每12个点对应的h记录下来，记为{h1，h2…hm}，对该集合使用快速排序法，得出h的最大值与此最大值，记 作hm、hm-1， 两 点 坐 标 分 别 对 应 为 (xm，ym)、(xm-1，ym-1)。分别以这两个坐标点作为起点，向AB做垂线，得到以下垂线方程：将轮廓链上的点集{(x1，y1)，(x2，y2)...(xi，yj)}，i∈ [0，479]，j∈ [0，639]通 过 计 算 得 到 的 点 记 作 (xl，yl)、(xl-1，yl-1)， 取(xm，ym)与(xl，yl)间距离和(xm-1，ym-1)与 (xl-1，yl-1)间距离较大者就是最长截线宽。

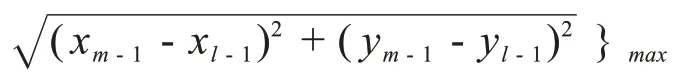
3 结果与分析

3.1 子叶张开角度

随机选择100个实验样本，对比最小外接圆算法得出子叶张开角度与实际张开角度，其中表3为其中的四组实验结果，对误差取绝对值，其最大误差为0.64°，最小误差为0.16°，平均误差为0.42°，可以满足计算子叶张开角度的精度要求。

表3 子叶张开角度误差表

3.2 最长截线宽度

随机选择100个实验样本，对比“垂直法”得到的最长截线宽度与实际最长截线宽度，表4中是随机抽取的6 次实验结果，最大误差为8 个像素，最小误差为1个像素，平均误差为3.6个。

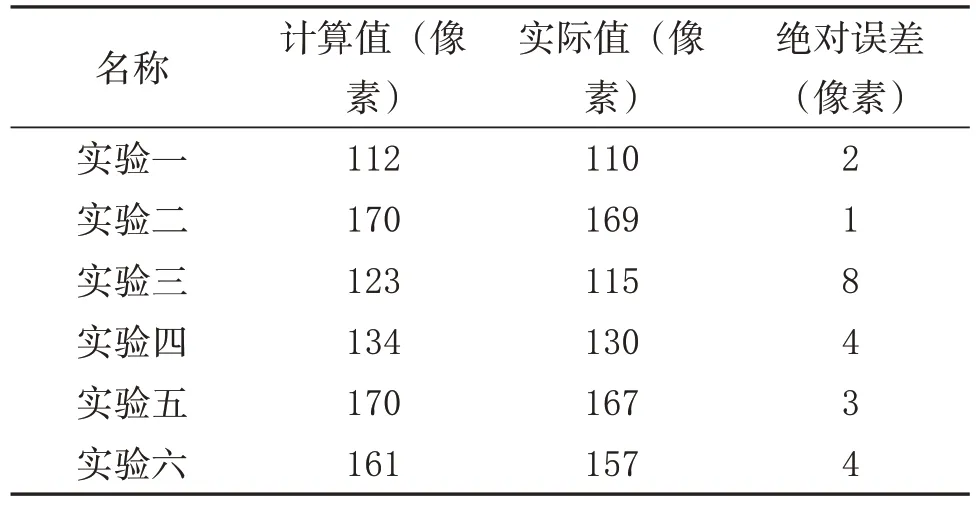
表4 最长截线宽度误差表

4 结论

通过研究机器视觉视角下砧木苗参数的提取，结果表明，子叶张开角度和最长截线宽度的求解精度都比较高，可以满足下一步取苗需求。该方法可以应用于自动嫁接机中，使任何张开角度的砧木苗被取苗后保持同一姿态。