分布式涵道风扇喷流对后置机翼的气动性能影响

张阳，周洲，郭佳豪

西北工业大学 航空学院，西安 710072

随着无人机气动布局的深入研究，垂直起降(Vertical Take-Off and Landing, VTOL)固定翼无人机以其方便起降、高速巡航的优势受到越来越多的关注[1-3]，极具代表性的有德国“百合”无人机、XV-24“雷击”无人机、NASA的GL-10验证机、XC-142A运输机等多种型号。以上型号无人机普遍采用分布式电推进(Distributed Electric Propulsion, DEP)来提供无人机垂直起降的升力，而DEP系统在近年来也成为研究热点，被认为是下一代飞行器设计最具潜力的动力布局形式之一。DEP无人机利用推进-气动耦合效应大幅改善空气动力特性，减小机翼面积从而降低结构重量，推进器无高压涡轮叶片且通过功率的分散可进一步减缩气动噪声总声级，分布式推进系统结合推力矢量技术可为无人机提供直接力控制从而降低飞机对尾翼和操纵舵面的依赖，多推进器的冗余能提供更可靠的推力保障，因而较传统电推进无人机具有更高的气动效率、载运能力、环保性以及在飞行控制与推力提供方面的鲁棒性[4-6]。

在无人机垂直起降的过程中，零速度来流问题导致的升力部件失效一直是VTOL技术的研究重点，而分布式电推进以其强烈的喷流提供了起飞状态下较高的气流速度，从而使升力部件产生可供垂直起降的气动力。但同时复杂的喷流效应也非常显著，其尾流通常带有切向和径向的速度分量，并且由于涵道桨毂的存在，气流扰动更加强烈，柱状喷流截面的压力、速度分布等非线性现象显著，也由此引起了雷诺数和湍流度的多变性[7-8]。机翼处于分布式电推进的喷流中，不仅受到上下洗气流的耦合影响，并且常伴有流动分离、分离泡、展向涡结构等现象[9-10]。

国内外的研究者面对分布式电涵道带来的复杂喷流的气动影响，主要进行了以下研究工作。Rodriguez[11]通过与常规吊挂式发动机布局对比，发现采用分布式动力的飞行器的推进效率能提高2%以上。Lundbladh[12]从总体设计的角度研究了发动机的数目对采用分布式动力飞行器的巡航效率和油耗的影响，发现埋入式动力系统能够减小起飞重量并降低油耗。Wick等[13]对比了翼下布局的分布式动力推进系统与常规发动机的差异，分析了分布式动力的数量等参数对全机的气动影响。Perry等[14]通过实验方法及数值模拟研究了翼上分布式电推进布局的动力-机身气动耦合特性，验证了边界层吸入效应的有效性。Kerho[15]通过数值计算分析了翼上分布式电推进布局在边界层吸入方面的气动优势，研究了机翼气动力与电涵道推力间的气动干扰问题。

在喷流增升方面的研究主要集中在机翼上表面吹气布局、吹气襟翼和机翼环量控制方面。Marcos和Marshall[16]通过实验确定了上表面动力增升布局合理的数值模拟方法。Maita等[17]通过实验验证了动力侧栏在上表面吹气布局中增升的潜力。焦予秦等[18]通过实验对上表面吹气、吹气襟翼的增升机理进行了分析。龚志斌[19]、白俊强[20]等针对大型运输机吹气襟翼构型验证了该布局的高升力效应。Li等[21]通过数值模拟对吹气多段襟翼的布局参数进行了研究。Englar等[22]对上表面吹气布局和环量控制实验进行了分析总结。Pfingsten和Radespiel[23]通过实验和数值模拟分析了某种机翼环量控制布局在增升方面的气动优势。

已有研究的主要垂直起降动力策略是推力竖直向上，主要对象是翼上分布式电推进的布局形式，主要技术是上表面吹气和吹气襟翼的应用，而缺少对水平安装的分布式电推进-机翼拉进式布局的气动特性研究。因此，本文以分布式电推进垂直起降无人机的零来流起飞问题为研究背景，结合推力矢量的设计思路，同时利用涵道风扇喷流带来的机翼气动力，以动力系统-升力部件耦合设计来实现整个系统竖直向上的合力接近涵道风扇的净推力为研究出发点，基于计算流体力学(Computational Fluid Dynamics, CFD)方法，使用商业软件Fluent对分布式涵道风扇-机翼构型的喷流气动特性进行了高精度准定常的数值模拟。通过对涵道单元/涵道-机翼的实验验证了零来流条件下数值计算方法的可靠性和高效性，主要研究了分布式涵道风扇-机翼构型的动力特性及气动优势，进而分析了分布式涵道风扇转速对机翼影响的相似性，涵道风扇间距对机翼的气动影响，最后研究了涵道风扇旋转方向给机翼带来的喷流气动耦合影响。

1 数值模拟方法及验证

1.1 数值模拟方法

本文采用多重参考系(Multiple Reference Frame，MRF)/动量源方法(Momentum Source Method, MSM)结合结构/非结构混合网格技术基于k-ωSST(Shear Stress Transport)湍流模型准定常求解雷诺平均Navier-Stokes(RANS)方程。空间离散方法采用二阶迎风MUSCL插值的Roe格式，时间离散与推进采用隐式AF(Approximate Factorization)方法。

1) MRF

MRF是一种对旋转单元体稳态近似的准定常数值模拟方法，能够求解得到充分发展的尾迹及流场。相比于非定常求解方法，MRF在计算代价和计算精度方面都具有一定优势，在定轴旋转体的气动计算中应用广泛[24-25]。

使用多重参考系方法进行求解时，根据网格分区的思想需要将整个计算域划分为静止流域和运动区域。运动区域为包围螺旋桨的封闭小圆柱面，小圆柱面外与远场边界之间的区域则为静止区域。小圆柱面作为连接2个区域的交界面，起着传递流场信息的作用。在MRF中，惯性坐标系内的绝对速度V与旋转坐标系内的相对速度Vr存在以下关系式：

V=Vr+Ω×r

(1)

式中：Ω为定常转速;r为位置向量。

对式(1)关于时间求导，则有

(2)

将式(2)代入Navier-Stokes控制方程中便得到MRF方法下以绝对速度表示的控制方程，方程主体形式未发生变化，仅在等式右端增加了源项：

a·S

(3)

式中：Q为守恒变量;F、G、H为3个坐标方向上的无黏通量;Fv、Gv、Hv为3个方向上的黏性通量;S为源项,其表达式为

(4)

其中:ρ为密度;a为0或1的常数，当求解惯性坐标系下的Navier-Stokes方程时，无需计算源项，此时a=0，当求解旋转坐标系的控制方程时，a=1。

2) MSM

MSM是将叶素理论同CFD方法耦合，用于求解旋转流场的一种高效简化方法。该方法首次由Rajagopalan和Fanucci[26]在1985年提出，后经多人发展[27-29]，对多桨叶旋转运动复杂流动问题求解具有一定的可靠性，并且可以显著减少计算成本，得到较为准确的速度和压力分布。

动量源方法用薄盘代替桨叶，在薄盘内采用叶素理论对桨叶载荷进行计算，转换成动量源项，加入Navier-Stokes方程进行求解，以此对桨盘进行模拟。设单个桨叶在1个周期内旋转用时为t0：

t0=2π/ω

(5)

式中:ω为角速度。对于桨盘中的网格单元，假设其所占圆周角度为dφ，则单个桨叶旋转dφ用时为tdφ：

tdφ=dφ/ω

(6)

将对应叶素截面作用力dF在1个周期内的作用效果等效到该网格单元上：

dF′=dF·tdφ/t0

(7)

对于N片桨叶，经过等效处理，便得到动量源S:

S=-N·dF′/Vc=-N·dF·dφ/(2π·Vc)

(8)

式中:Vc为网格单元的体积。通过坐标变换得到S在x、y、z方向上的分量Sx、Sy、Sz，最后将其加入对应网格单元控制体的动量方程中，参与迭代求解。

1.2 涵道动力单元数值方法验证

对直径Φ=150 mm的涵道风扇在转速11 000 r/min、零来流工况下进行了拉力和尾迹测量。实验设备包括ATI六分量天平、可移动五孔探针、空速管及配套数据采集装置、老鹰树数据记录仪(转速、温度传感器)等，实验台架如图1所示。实验测得涵道风扇拉力为33.612 N，涵道风扇下半部分径向截面尾迹及轴向距喷口20 mm位置处测量的时均结果如图2所示(图中黑框区域为五孔探针安装位置，真实尾迹参照左侧区域；图中坐标表示测量区域的位置区间,V表示速度)。

图1 涵道动力单元实验台架Fig.1 Experiment bench of ducted fan

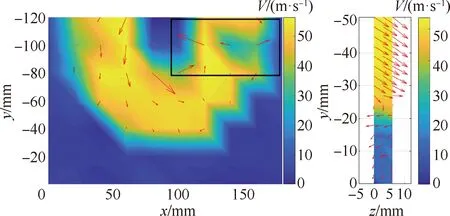
图2 涵道风扇径向及轴向截面尾迹Fig.2 Radial and axial section wake of ducted fan

对该模型的数值计算分别采用MRF和MSM这2种方法。MRF需要构建桨叶运动区域的网格，该区域采用非结构网格生成，整体网格为结构/非结构混合网格。而MSM由于对桨叶进行了简化处理，仅需构造涵道壁面及桨毂模型，其对应网格采用结构网格划分。涵道风扇建模及混合/结构网格(网格量约为500万)划分如图3所示。

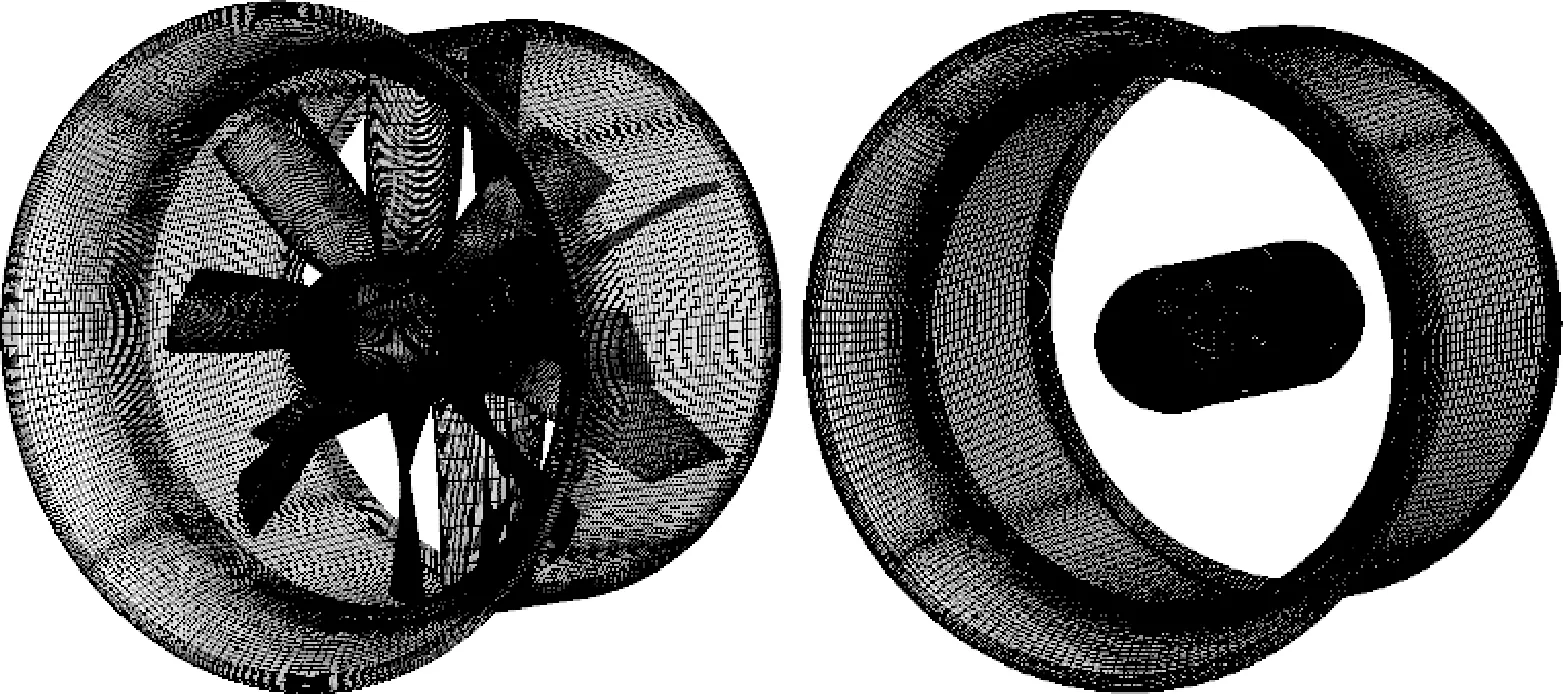
图3 涵道动力单元计算模型混合/结构网格Fig.3 Hybrid/structured mesh of ducted fan calculation model

数值模拟时设置来流速度为V∞=0.34 m/s(马赫数Ma=0.001)，得到的拉力数值如表1所示，尾迹截面速度分布如图4所示。表1中T表示涵道风扇拉力，E1表示数值结果与实验结果的误差，TLip表示涵道壁面及桨毂拉力。由于MSM得到的计算结果仅包含涵道壁面及桨毂的拉力，故MSM的计算误差是与MRF计算得到的相应部分的数值(TLip)进行对比。从拉力的对比可以看到，2种准定常方法的数值计算精度较高，误差均在5%以内，具有工程应用的可靠性和高效性。而尾迹的计算结果与实验的测量结果非常接近，相比于MRF，MSM由于模型的简化处理，得到的尾迹比较均匀，轴向速度稍大，但是其计算效率更高。以上数值计算结果充分说明了MRF和MSM在模拟涵道风扇单元时的可靠性和有效性。

表1 涵道动力单元数值计算与实验结果对比

图4 数值模拟得到的径向/轴向尾迹Fig.4 Radial and axial section wake with numerical simulation

1.3 涵道耦合机翼方法验证

由于机翼耦合涵道风扇的实验可参考的文献较为少见，本节针对该构型开展了实验验证，实验设备包括ATI六分量天平、配套数据采集装置、老鹰树数据记录仪(转速、温度传感器)等，实验台架如图5所示。依然使用Φ=150 mm的涵道风扇(唇口有所改变)，在11 000 r/min、零来流工况下，对NACA0012机翼的气动力进行了测量，其迎角相对涵道风扇喷流为25°。同样采用MRF和MSM分别进行数值方法验证，建模及结构/非结构混合网格(网格量约800万)划分如图6所示，计算结果如表2所示。

图5 涵道耦合机翼实验台架Fig.5 Experiment bench of ducted fan and wing

图6 涵道耦合机翼计算模型网格Fig.6 Computational mesh of ducted fan and wing

表2中：Tc为无后置机翼时涵道风扇的推力(MSM对应的Tc值为涵道壁面和桨毂的拉力)；Tv为有后置机翼时涵道风扇在竖直方向上的力；L、D、K分别为机翼的升力、阻力和升阻比；E2、E3分别为机翼升力和阻力的数值结果与实验结果的误差；Steps表示2种数值模拟方法计算收敛时的迭代步数。需要说明的是，实验对比以涵道风扇转速固定为前提。增加后置机翼使涵道风扇的输入功率增大了201.684 W，推力提高了1.831%，同时产生了0.528 N的负升力，但是量值较小，对整个系统的影响有限。对于机翼的气动特性来说，相比于实验结果，数值计算得到的机翼升力误差在5%以内；而机翼计算阻力稍小，误差小于15%，由此导致了升阻比偏大。

总的来说，MRF和MSM对涵道风扇的数值模拟精度良好，数值模拟误差范围满足工程应用的需求，同时MSM计算效率较高，相比于MRF节省了近一半的计算代价。以上数值计算结果充分说明了本文使用的计算方法在工程应用时的可靠性和高效性。

2 分布式涵道风扇气动优势

在充分验证数值计算方法的基础上，本节开展了零来流条件下(数值计算采用的来流速度均为V∞=0.34 m/s(Ma=0.001))分布式电涵道的气动优势及喷流特性研究。

使用的涵道风扇模型与1.2节一致，对比了分布式涵道风扇与单个涵道风扇对机翼的诱导增升效果，涵道风扇与机翼的相对位置关系(x,y,α)为(200 mm, 40 mm, 20°)，如图7所示。分布式涵道风扇(4个)沿展向排布，涵道转轴间距dz=200 mm；涵道风扇转速均为11 000 r/min，旋转方向为前视的逆时针方向。机翼弦长C=0.1 m，为了尽量减少翼尖涡带来的气动干扰，机翼展长尽量超出涵道风扇的喷流影响区域，翼展取b=2 m；2种构型的计算模型如图8所示，划分网格量为1 400万。由于分析对比时需研究桨叶拉力的差异，数值计算采用将桨叶等部件考虑在内的MRF方法，结果如表3所示。

图7 涵道风扇与机翼的相对位置Fig.7 Relative position of ducted fan and wing

图8 2种构型的计算模型Fig.8 Computational models of two configurations

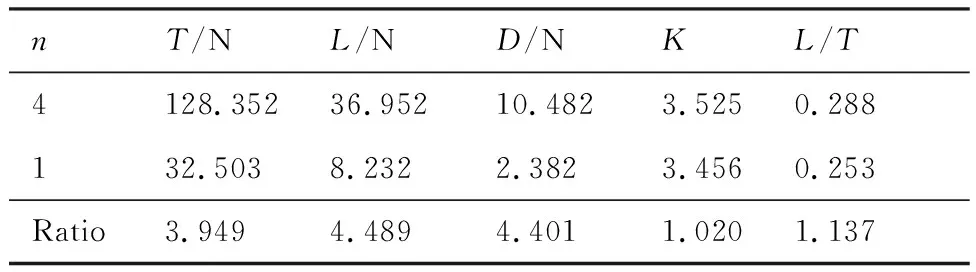
表3 2种构型气动特性对比

通过对比可以看到，相比于单个涵道风扇，分布式涵道风扇总拉力接近其4倍，对其后方的机翼诱导产生了约4.4倍的升力及阻力，升阻比和升推比的数值也略有提高。这说明分布式涵道风扇能够对其后方机翼产生增升的气动优势，具有较好的气动诱导效果。

下面通过机翼表面的流动特征及空间流态来进一步分析气动诱导机理，2种构型的表面静压(p)分布、极限流线以及空间流态如图9所示。可以看到，相比于涵道单元-机翼构型，分布式涵道-机翼构型对机翼的喷流影响面积明显增大，同时上下翼面低压/高压区域能够形成较为连续的压力变化；对喷流影响区以外的翼面气流形态有一定有利影响，但是总体都较为紊乱，并伴有明显的展向流动。

图9 2种构型的表面流态与空间流态Fig.9 Surface and space flow patterns of two configurations

对2种构型分别截取x/C=0及x/C=0.5处沿展向的静压分布，如图10所示(DEP表示分布式涵道-机翼构型，Solo表示涵道单元-机翼构型，箭头表示涵道喷流对机翼的上/下洗方向)。可以看到，对涵道单元-机翼构型来说，在上翼面临近喷流影响的边缘处(上翼面绿圈)，静压迅速回落接近环境静压，而下翼面受到喷流的上/下洗作用形成了一高一低2个高压峰值(下翼面绿圈表示较低峰值)。相比于涵道单元-机翼构型，分布式涵道风扇对上下翼面的诱导静压峰值相差不多，但是由于相邻涵道风扇的喷流耦合作用，一方面，上翼面的静压难以恢复到环境静压(上翼面红圈)，另一方面，在下翼面较低的峰值受到临近涵道喷流较高压力峰的激励，产生了较高的压力峰(下翼面红圈的较低峰值受到左侧高压峰的激励)，同时在翼面上能够形成更宽的连续的静压变化。基于分布式涵道风扇后方喷流耦合对上/下翼面的诱导作用，机翼整体气动特性得到了一定的改善。

图10 展向静压分布Fig.10 Spanwise static pressure distributions

另外值得注意的是，由于在数值模拟时4个涵道风扇的旋转方向均为前视的逆时针方向，故对于上翼面来说，4个涵道风扇沿-z方向的喷流负压在1号涵道风扇(涵道风扇标号见图8(b))的喷流区形成了一定的叠加作用，造成该区域静压峰值最低；而对下翼面来说，涵道风扇的抽吸作用使得外围机翼的流动向喷流段聚集，在1号涵道喷流处的高压与外围流动静压叠加，造成该区域下表面静压峰值最高。也由此造成了4个涵道风扇拉力上的差异，各个涵道风扇的部件拉力见表4。

表4中Rob表示转子桨叶，Stb表示静子桨叶，Lip表示涵道唇口,下标1～4分别对应4个涵道风扇。可以看到，位于内侧的2号和3号涵道风扇的转子桨叶和涵道唇口的拉力均偏小，导致了总拉力相对较小，参照图9(b)的空间流态，外侧涵道风扇的抽吸作用影响了内侧2个涵道风扇的进气效果，空气流量的减小导致桨叶效率下降，同时影响了涵道唇口的吸力作用，使得内侧2个涵道风扇的拉力受到损失。

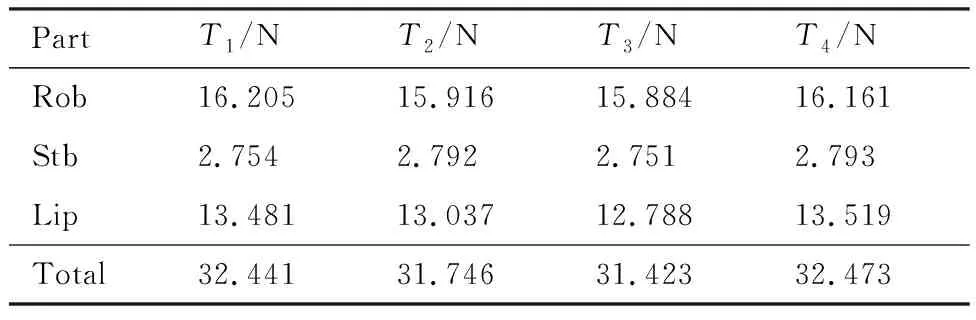
表4 分布式涵道风扇各个部件拉力Table 4 Force of each component of distributed ducted fans

由以上分析可以看到，分布式涵道风扇动力单元的拉力大小(转速)、间距以及桨叶旋转方向对涵道风扇本身以及机翼会产生不同的气动诱导效果，下文将继续研究分布式涵道转速、间距及旋转方向的气动影响。

3 分布式涵道风扇喷流气动影响

3.1 转速的影响

涵道风扇的转速影响着喷流流速以及气流的湍流度[7]，会对后方机翼的气动特性产生决定性的影响。本节通过调整分布式涵道风扇的转速(nr=1 000～13 000 r/min)，来研究机翼的气动特性变化及流场形态的演化。计算过程中涵道风扇与机翼的相对位置关系、涵道风扇旋转方向与前文一致，每个涵道风扇的转速同样保持一致。计算结果如图11所示。可以看到，随着涵道风扇转速的提高，机翼的升力、阻力均在增大，升阻比维持在3.3～3.6之间，但是升推比则趋于降低。

图11 转速对机翼气动特性的影响Fig.11 Influence of rotating speed on aerodynamic performance of wing

为分析机翼气动特性变化的原因，对1 000、7 000、11 000 r/min转速下机翼表面的流态和流线变化进行对比，如图12所示(转速11 000 r/min的表面流态参见图9(b))。可以看到，涵道风扇转速越大，喷流影响区域的翼段表面上的流线越光顺，流动状况不断改善，上表面的负压区域不断增大，下表面的高压区域逐渐连续成一片；对于翼段喷流区域之外的外翼段来说，翼段上的流线沿弦向的流动性有所改善。在1 000 r/min时上翼面30%C附近出现了明显的流动分离情况，而在11 000 r/min时流动分离的位置有所推迟，发生在约60%C处，这说明高转速的涵道风扇极大地丰富了机翼边界层内湍动能程度，改善了流动附着的情况。

图12 机翼表面流态Fig.12 Surface flow patterns of wings

进一步研究机翼沿弦向的气动特性，截取2号涵道风扇对称面位置对应的机翼剖面，其静压分布如图13所示，3种不同转速下剖面的速度场特征如图14所示(为表现几种转速下流态的相似性，对图例中的速度尺度有所调整)。

图13 翼型静压分布随转速的变化Fig.13 Variations of static pressure distributions of airfoil with rotating speed

图14 3种转速下流场截面的速度场形态Fig.14 Velocity fields of flow section with three different rotating speeds

通过不同转速下的静压分布对比可以看到，随着涵道风扇转速提高，截面翼型上表面压力越来越小，下表面压力越来越大；同时各个转速对应的压力曲线形状非常相似：前缘吸力峰位置接近，随后上表面压力增大。但是随着喷流效应的增强，下表面的高压逐渐影响到翼型后缘上表面，使得逆压梯度有所增强但不至于发生流动分离，翼型全过程并未失速。

对比1 000、7 000、11 000 r/min转速下的截面速度流态可以看到，尽管存在转速影响的流速等方面数值上的差异，但是对截面翼型来说其附近的流场形态十分相似，故可以认为在翼段相对位置、安装角等参数不变时，涵道风扇转速的变化仅仅影响对称截面翼型具体的速度、静压等数值大小。

3.2 间距的影响

分布式涵道风扇的间距不仅对涵道风扇单元本身的动力特性存在影响，更影响着机翼的诱导增升效果。本节涵道风扇与机翼的相对位置、涵道转速及转向等均与3.1节保持一致，仅改变了涵道风扇的间距：dz=200，250，300 mm。3种间距下各个涵道风扇部件的拉力对比见图15。可以看到，随着涵道风扇间距的增大，各个涵道风扇的静子桨叶带来的拉力变化较小，拉力差异主要来自于转子桨叶和涵道唇口。这主要是由于间距的增大改善了各个涵道风扇的进气效率，转子桨叶的效率有所提升，唇口壁面上的流动状态得到改善，进而提高了涵道风扇的拉力。

图15 不同dz下分布式涵道风扇各个部件的拉力Fig.15 Force of each component of distributed ducted fan with different dz

随着涵道风扇间距的增大，3种分布式涵道风扇构型总拉力持续增大，但是其后方机翼的气动特性变化规律则与之不同，气动力对比如图16所示。可以看到，随着涵道风扇展向间距的增大，机翼的气动特性并没有因此得到改善，反而升力、阻力以及升推比均在下降，而升阻比基本保持不变。这说明在分布式涵道风扇-机翼构型下，涵道风扇的总拉力并非影响机翼气动特性的唯一因素，涵道风扇喷流的耦合作用对机翼的诱导效果也较为强烈。

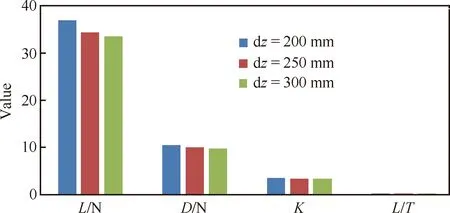
图16 分布式涵道风扇间距对机翼气动特性的影响Fig.16 Influence of distributed ducted fans spacing on aerodynamic performance of wing

为研究涵道风扇喷流的耦合作用，对3种间距下的沿机翼展向x/C=0及x/C=0.5的压力分布进行了对比，见图17。可以看到，涵道风扇间距的增大不仅扩大了机翼展向受喷流影响区域的宽度，也影响了涵道单元对应静压峰值差异，同时改变了喷流区域之间静压的过渡状态。静压峰值变化的原因与涵道风扇单元的拉力相关，同时受到涵道风扇旋转方向以及喷流耦合的综合影响。而随着涵道风扇间距的增大，尽管机翼展向受喷流影响的面积增大，但是涵道单元之间的区域经过气流耦合，其静压则趋于减小，甚至在dz=300 mm 时出现上下翼面的静压值相同的情况，这种涵道喷流的弱耦合作用使得静压的过渡一定程度上削弱了机翼的整体升力。相比于较大离散度的分布式涵道风扇-机翼构型，dz=200 mm 间距的构型在机翼静压变化的连续性上更优，靠右侧的涵道风扇(2、3、4号涵道风扇)对下翼面产生的小静压峰值受到临近涵道喷流能量激励，获得了更大的静压变化，使得其整体翼面上的静压分布更接近椭圆形升力分布，也由此获得了较好的气动诱导效果。

图17 不同dz下的展向静压分布Fig.17 Spanwise static pressure distributions with different dz

图18为3种间距下机翼对称截面翼型的静压分布对比。可以看到，dz=200 mm间距时上下翼面的静压均受到了喷流诱导作用，下翼面的高压尤其明显；而随着间距的增大，上翼面的静压几乎不发生变化，同时下翼面的高压越来越小，整个截面翼型的升力损失较大。这从侧面说明了分布式涵道风扇间距较小时，喷流之间为强耦合作用，对机翼上的气动诱导效果也较强。

图18 机翼对称截面翼型的静压分布Fig.18 Static pressure distributions of symmetric section of airfoil

3.3 旋转方向的影响

自由来流下的机翼通常会在翼梢产生较强的由下翼面卷起的翼尖涡，上翼面会受到涡系的影响而削弱升力贡献。分布式涵道风扇由于动力单元数量较多，使得其设计余度较大，可以通过调整涵道风扇的旋转方向来弱化翼尖涡对上翼面的不利影响，一定程度上提高机翼的气动特性。而本节研究的机翼展长与前文一致为b=2 m，远远超出分布式涵道风扇的喷流影响区域，因此不考虑喷流和翼尖涡的相互影响，着重研究分布式涵道风扇喷流耦合作用对机翼带来的气动影响。

考虑到分布式涵道风扇的旋转方向研究需要进行大量的建模及数值计算过程，为了减小计算代价，兼顾计算精度与计算效率，同时考虑改变涵道风扇旋转方向的可设计性，本节采用MSM对涵道风扇进行数值模拟。计算状态与3.2节一致，涵道风扇间距取dz=200 mm，改变涵道风扇单元的旋转方向，形成了6种不同转向组合。为方便说明，本文规定前视涵道风扇绕轴逆时针旋转以0表示，前视涵道风扇绕轴顺时针旋转以1表示，按照从1号～4号涵道风扇的顺序，6种转向组合分别为：0000，1100，0011，1010，0101，1001。以上6种不同的转向组合对机翼气动诱导效果的计算结果见图19。

图19 转向组合对机翼气动特性的影响Fig.19 Influence of rotating direction on aerodynamic performance of wing

可以看到，旋转方向对机翼产生了较为明显的气动影响，其中0011、0101旋转组合使机翼得到了较好的气动特性，而1010、1100旋转组合对应的机翼升力特性、升阻比均较差。另外需要说明的是，经过计算,6种转向组合的涵道唇口拉力相差很小，最大和最小的唇口拉力仅有0.346%的差距。下面对以上4个旋转组合进行具体的流场分析，如图20所示。为方便说明，图中的上洗影响以UP标明，下洗影响以DW标明。

图20 不同转向组合的机翼表面流态和空间流态Fig.20 Surface and space flow patterns of wing with different rotating directions

从以上表面流态及空间流态的对比可以看到，4种旋转组合在喷流影响区的差异主要是上洗和下洗影响的不同造成的。从表面流态可以看到，不同的转向组合对机翼表面的影响主要在于上翼面的低压区/下翼面的高压区的相对位置变化以及流线沿展向方向的变化：靠近上洗影响的上/下翼面静压较高，而靠近下洗影响的上/下翼面的静压较低，流线由上洗区域向下洗区域的流动性更强。

另外，不同转向组合的空间流线形态也存在较大差异。结合空间流线对1号和4号涵道风扇的转向影响进行分析，0011、0101旋转组合在靠近外翼的位置使气流产生下洗作用，并且考虑到机翼本身存在20°的安装角，下洗气流与机翼本身对气流的导向较为一致，故在该位置附近的流动较为平顺，同时下翼面流动得到收束效果更好；而对于1010、1100旋转组合，靠近外翼位置喷流的上洗与机翼导流方向存在冲突，使得该处流动出现了向外侧扩张的趋势，流动变得更加复杂。

下面通过研究4种不同转向的分布式涵道风扇机翼展向x/C=0及x/C=0.5的压力分布来对比分布式涵道风扇喷流作用的影响，如图21所示。

图21 不同转向下的展向静压分布Fig.21 Spanwise static pressure distributions with different rotating directions

对展向x/C=0处来说，上翼面的差异主要是1号和4号涵道风扇静压峰值的大小不同，0011和0101两组的静压相比于1100和1010更低。而下翼面的静压分布情况差异较大，0011和0101两组的差别源于2号和3号涵道风扇转向相反，0011组相比于0101组静压分布更均匀，高压峰值间距更小，使得在整个喷流影响区域内高压维持得更好；1100组和1010组的差别同样源于中间2个涵道风扇的旋转方向的差异，类似地，1100组高压过渡更为平缓，上下翼面压差损失更小。

对展向x/C=0.5处来说，上下翼面静压的变化规律与x/C=0较为一致，但是下翼面的静压变化出现了新的特征：相比于0101组，0011组在中间2号和3号涵道喷流区域明显受到1号和4号涵道喷流的影响，原本较小的峰值被激励为与1号、4号峰值相当的高压，进一步提升了机翼的升力特性。1100组相比于1010组也是类似效果。

总的来说，分布式涵道风扇的旋转方向对机翼的升力特性有一定影响：靠近外侧的涵道风扇单元的旋转方向对上翼面产生向机翼外侧的速度分量时整体升力特性较好，外侧涵道风扇对机翼的静压变化产生了更强的诱导效果；机翼左右两侧对称旋转方向的安装方式使得下翼面喷流影响区域的高压过渡更加平缓，静压数值更加连续，同时合理的旋转方向也会使得内侧喷流被外侧喷流所激励，对机翼的升力特性产生更好的诱导效果。

4 结 论

本文通过MRF及MSM对分布式涵道风扇-机翼构型进行数值模拟，得出以下结论：

1) 相比于涵道风扇单元，分布式涵道风扇由于其喷流的耦合作用对机翼产生更加优异的气动诱导效果：分布式涵道风扇总拉力接近4倍的涵道风扇单元，机翼的升力特性提高了约4.4倍，升阻比及升推比也略有提升。

2) 分布式涵道风扇不同转速下，截面翼型静压分布和流场特征呈现一定的相似性，但具体的流场参数随转速变化；随着转速的提高，涵道风扇能够提供更加丰富的机翼边界层内的湍动能程度，使得喷流影响区域内翼面上的流线更加光顺，流动附着情况不断改善。

3) 在分布式涵道风扇间距较小时，涵道风扇喷流的强耦合作用会加强上下翼面的压力差值，从而获得较好的机翼气动特性。随着间距的增大，涵道风扇单元的进气效率得到改善，动力特性有所提升，分布式涵道风扇总拉力也不断增大，而机翼的气动诱导效果则趋于下降。

4) 分布式涵道风扇不同的旋转组合对涵道风扇的动力特性影响较小，总拉力最大差距仅有0.346%；而旋转组合对机翼的气动诱导影响较为显著：当涵道风扇旋转方向对上翼面产生向机翼外侧的速度分量时机翼升力特性较好，外侧涵道风扇对机翼的静压变化产生了更强的诱导效果；机翼左右两侧对称旋转方向的安装方式使得下翼面喷流影响区域的高压过渡更加平缓，静压数值更加连续，同时合理的旋转方向也会使得内侧涵道风扇被外侧喷流所激励，对机翼的升力特性产生更好的诱导效果。

以上对分布式涵道风扇-机翼构型的数值计算、涵道风扇特性分析以及喷流的强耦合气动诱导效果能够为分布式电推进垂直起降无人机提供分析参考以及设计依据。