威布尔型通用件配置方案评估及优化

徐立，阮旻智，李华，周亮

1. 海军工程大学 兵器工程学院， 武汉 430033

2. 海军工程大学 舰船与海洋学院， 武汉 430033

3. 海军工程大学 舰船综合电力技术国防科技重点实验室, 武汉 430033

航空、航天装备保障活动十分复杂，备件保障能力是影响装备保障效果的关键因素之一。通用件是在不同类型或同类型不同规格的装备中具有互换性的零部件单元[1]。通用件的使用不仅可缩短新产品设计开发周期，减少专用件的数量，简化生产制造过程，还可降低供应商提前期的不确定性，提高保障效率。通用件逐渐成为装备制造与保障领域发展的重点。与此同时，由于通用件使用范围广、频率高，与专用件相比，其短缺会带来更大范围的影响[2]。在通用件中，机械类部件如滚珠轴承、继电器、陀螺、电动机、航空发电机、齿轮等[3-4]部件寿命服从威布尔分布，应用广泛、需求量大。威布尔型通用件的保障效能——备件满足率能否满足装备保障需求是保障部门关注的重点和难点之一。

备件配置问题长期受到国内外学者的关注，提出了多种备件需求预测方法。一类是基于备件消耗的单项备件预测方法，该方法应用更新过程理论得到不同分布类型部件的平均备件需求量模型[5]，提出了基于需求的多分布类型备件预测方法[6-8]，但是这些模型形式较为复杂，难以通过解析计算得到封闭解，运用较为困难；另一方面，从备件保障效能出发，研究了多种备件配置评估优化模型[9-10]，反映备件配置对装备保障效能的影响。在装备实际保障过程中，备件配置方案根据装备任务特点，通常选用满足率作为制定备件配置方案的度量指标。文献[3]针对装备保障过程需求，给出了备件满足率的统计定义。程海龙等[11]在备件供应规划中分析备件满足率与备件短缺量的数学含义和物理意义，针对部件寿命分布服从指数分布的情况，在METRIC模型寻优方法基础上，考虑费用的影响，对比验证备件满足率和备件短缺量的适用范围。张志华等[12]针对备件满足率只有统计定义的问题，研究了单备件满足率和串联系统备件满足率的概率性质，给出了概率模型。Sapna[13]以排队论方法为基础，在系统趋于稳态时，得到系统不缺备件的概率。这些模型的求解以解析方法的形式给出，当系统备件种类多、数量大时难以通过解析方式给出备件配置方案与备件满足率之间的对应关系。在开展非指数部件的备件需求预测时，由于非指数分布部件保障效能计算过程较为复杂，一般采用等效思想将非指数分布部件的寿命等效为指数分布，以此来降低计算难度，提高计算效率。邵松世等[14]通过贝叶斯理论将有寿件的寿命等效为正态分布，提出了一种基于正态等效的有寿件备件方案确定方法。刘任洋等[15]通过可靠度等效方法将系统中的非指数单元转化为指数单元，将多指数单元表决系统等效为伽玛系统给出备件需求量解析方法。Perez和Montoro[16]提出一种新的分布位相型分布来替代其他分布，并采用马尔科夫到达过程预测备件需求。由于通用件使用范围广，装机数量多，在开展备件库存配置时有其特殊需求。Baker[17]研究了通用件策略对于安全库存水平的影响，独立于传统的Zσ原则给出了通用件储存策略。Gerchak和Henig[18]在多产品多零部件环境下，考虑产品需求服从一般分布，建立了多周期库存模型。Ma等[19]研究了多产品、多周期、多级装配、随机需求的通用件问题，考虑了通用件成本结构、补货提前期和装配时间等因素。Sengupta和Shun[20]综合部件通用性和供应链决策，给出了通用件收益评估方法。Deza等[21]介绍了一种根据部件通用程度进行库存控制的方法。

综合以上文献可知，在威布尔通用备件配置方案评估及优化方面存在以下3个方面的不足：① 备件满足率只有统计方面的定义，难以建立起威布尔通用备件保障能力评估指标与装备数量、使用情况及备件配置数量的联系；② 理论上计算备件数量为k时的备件满足率涉及单元寿命分布函数的k重卷积计算。而威布尔分布的k重卷积解析式较为复杂，难以推导得出该解析式，实际计算较为繁琐；③ 进行装备通用备件的需求量计算时，通常采用分别计算各装备的备件需求量，再将备件数量之和作为总的备件需求量的方法。这种计算方法容易造成通用备件的过度采购，引起资源浪费。本文针对威布尔通用备件保障能力评估及配置方案优化问题，采用等效原理，将威布尔型部件消耗过程等效为伽玛冲击过程，建立威布尔型通用备件满足率评估模型，并在备件满足率指标约束下，开展威布尔通用备件的配置方案优化。通过仿真对比验证本文所建模型及方法的计算精度和适用范围。为装备保障部门开展威布尔型通用备件配置方案评估与优化提供理论支撑和决策支持。

1 问题描述及模型假设

1.1 保障过程描述

假设某威布尔型通用件分别在N台装备中使用，已知该通用件在装备n中每年计划工作时间为Tn,1≤n≤N，当该通用件发生故障时，采用换件维修的方式排除故障。由于各装备工作时间的差异，装备n对通用件j会产生不同的备件需求，记为λjn，装备备件需求关系如图1所示。现在备件仓库需配置该通用件数年的备件，备件数量记为s。在整个观察周期内，备件数量能够满足各装备的备件需求的概率称为备件满足率。通常装备保障部门会对备件满足率设置指标要求，要求其不得低于门限值P0，要达到精确化保障的目的，需在已知装备工作计划的前提下，合理配置备件数量，以求在观测周期内，备件满足率不低于相关指标要求。

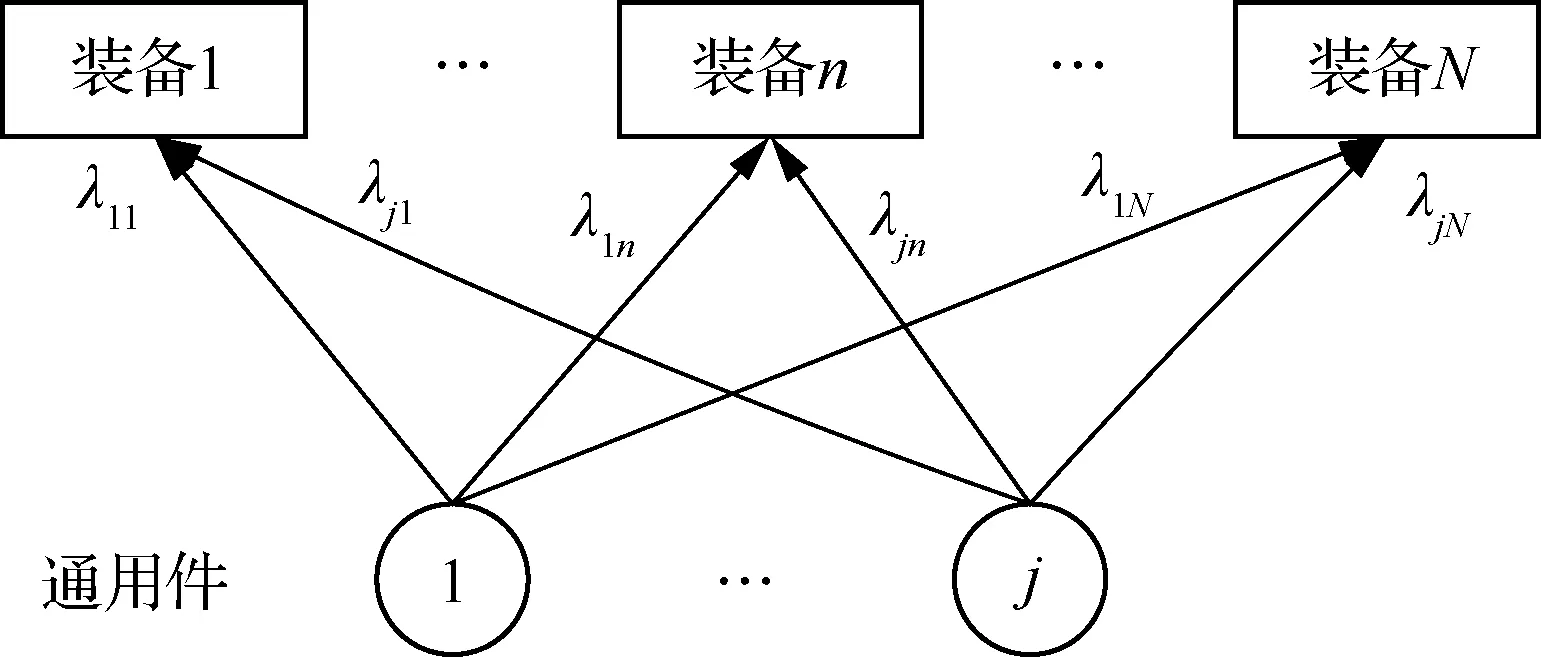
图1 通用件需求示意图Fig.1 Sketch map of demand for component commonality

1.2 模型假设

一般情况下，为使装备尽快投入使用，降低装备现场维修时间，装备使用现场通常对故障部件进行换件维修。另一方面，装备的部分通用件维修效益较低，不具备维修价值。除此之外，在装备批次采购部件之间的时间间隔内，开展临时订货周期较长。因此，为了研究的方便，本文在进行建模和优化时做如下假设：① 观测周期内不考虑通用件的补给；② 装备部件发生故障仅进行换件维修；③ 更换后的故障部件不进行修理。

2 威布尔型通用件备件满足率模型

2.1 等效原理

对于部件寿命X服从形状参数为m,特征寿命为η的威布尔分布，记作X～W(m,η)，则可得其平均寿命为

(1)

方差为

(2)

式中:Γ(·)表示Gamma函数。

根据等效的原则，若需威布尔分布X～W(m,η)等效为伽玛分布X′～Ga(α,λ)，则需二者的平均寿命与方差相等。伽玛分布其均值为

(3)

方差为

(4)

联立方程式(1)、式(2)、式(3)、式(4)可得

(5)

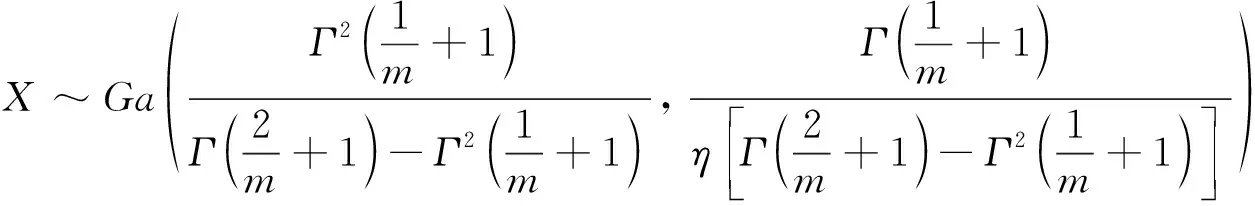
2.2 威布尔型通用备件满足率模型

对于单个伽玛型部件，若其寿命X～Ga(α,λ),工作时间为Ti，则其在工作时间内发生故障的概率为

(6)

在可靠性理论中，部件寿命服从伽玛分布可用冲击模型进行解释。假若产品能经受若干次外界冲击，但当产品受冲击次数累积到α次时就产生失效。此时，产品寿命T就是第α次冲击来到的时间[22]。根据伽玛分布的冲击理论，若某部件i，其备件配置数量为si,则在任务期间Ti内，在故障率为λ保持不变的情况下，若单个部件受α次冲击导致故障，相应的，在有si个备件时，其不能承受α(si+1)次冲击的概率为

(7)

当si=0时，表示对部件i不配置备件。

则备件配置数量为恰能够满足装备需求的概率密度函数为

f(si,Ti)=F(si-1,Ti)-F(si,Ti)

(8)

即为

(9)

当si=0时，表示对部件i不配置备件恰能满足装备备件需求的概率。

根据卷积性质，设W与Y为2个相互独立的随机变量，其密度函数分别为pW(w)和pY(y)，则其和Z=W+Y的密度函数为

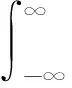
若对于装备1中部件i，任务时间为T1时，需si1备件满足其正常运转；若对于装备2中部件i，任务时间为T2时，需si2备件满足其正常运转；如此类推，对于装备n中部件i，任务时间Tn，需sin备件满足其正常运转。T1至Tn分别表示在观测期内，装备1到n的计划工作时间，相互独立。则在一定观测期内，对于不同任务时间、不同装备，当备件总量为si时，恰能满足装备备件需求的概率为

f(si)=f(si1,Ti)*f(si2,Ti)*…*f(sin,Tn)

(10)

式中：“*”号表示卷积，si=si1+si2+…+sin，若si=0，则表示对于装备1至n均不配置备件时，恰能满足装备备件需求的概率。

则对于装备1到n，配备备件数量为si(si可为0)时，满足这些装备备件需求的备件满足率为

(11)

3 备件配置方案优化方法

备件配置优化采取逐步优化的方法开展，设置满足率门限值P0。

步骤1初始化备件库存，令si=0;若部件i寿命服从X～W(m,η)的威布尔分布，根据公式(5)，将其等效为X～Ga(α,λ)的伽玛分布，求取等效后的α和λ。

步骤2根据式(9)、式(10)、式(11)求取各观测时间内，装备在总的备件配置数量为si时的备件满足率Pm。

步骤3若Pm≥P0,则输出此时的备件配置方案，即为所求；否则，令si=si+1；转步骤 2，继续开展相关迭代，直至Pm≥P0输出最终优化后的备件配置方案。

4 仿真算法设计与分析

在装备数量为N，部件寿命服从威布尔分布，参数为m,η，各装备任务时间T=[T1,T2,…,TN]确认之后，开始仿真，所有部件按照分布规律产生故障。每次故障后，判断故障发生时机是否在任务时间范围内。若是在任务时间范围之外，则认为不需要备件；若是在任务时间范围内部件发生故障，则产生一次备件需求，此时若有备件，则备件满足，同时备件库存量减1，若无备件，则备件满足失败。如此，直到各装备的任务时间均达到观测周期内的计划时间，判断本次仿真备件数量是否满足需求，如此直至simN次仿真结束，统计成功满足备件需求的总次数M，仿真过程见图2。当实验次数足够大时，根据大数定律，两者之比即可作为备件满足率的近似值，即为

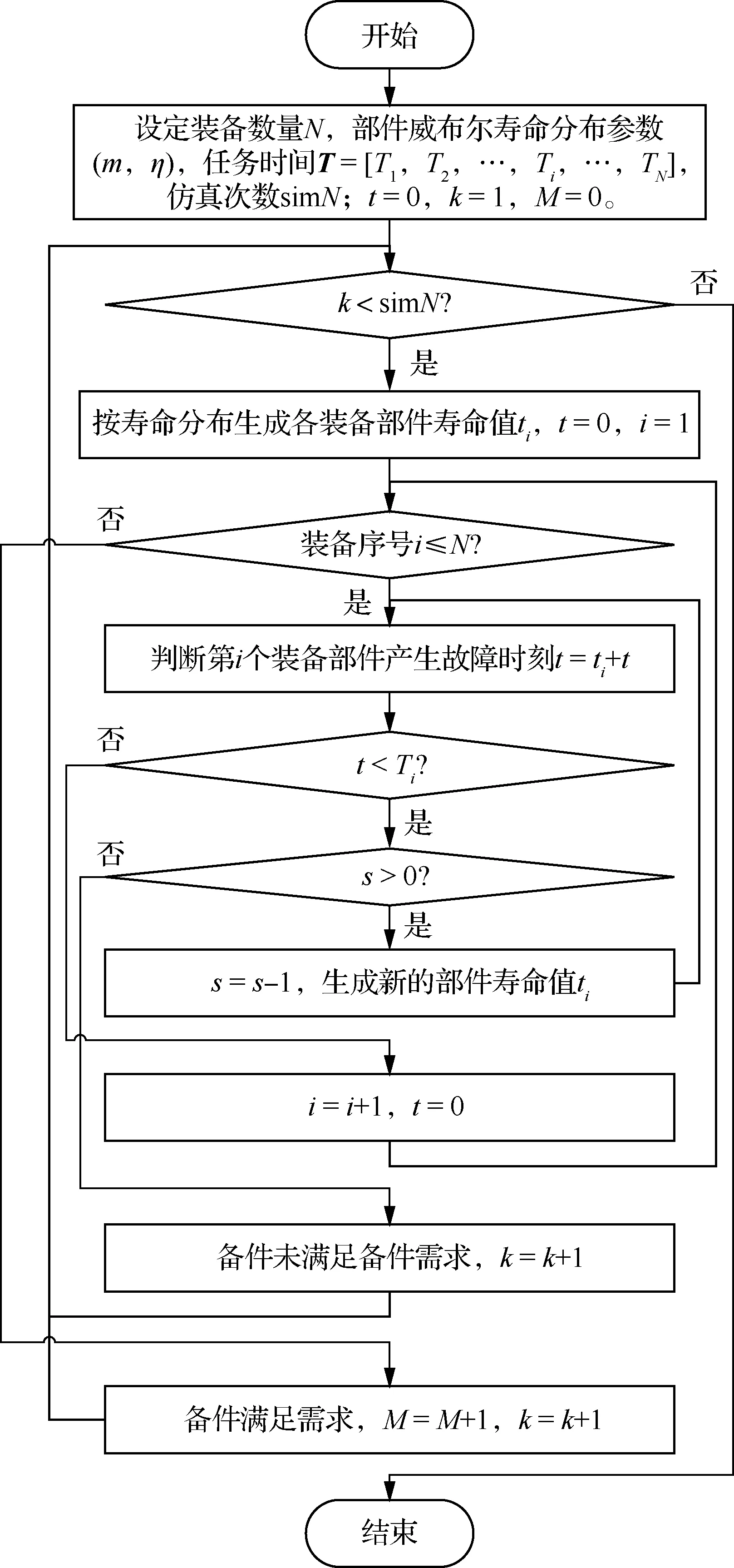
图2 仿真流程图Fig.2 Simulation flow chart

(12)

5 算例分析

5.1 仿真分析

选取威布尔型各部件寿命分布参数如表1所示。

表1 各部件寿命分布参数Table 1 Life distribution parameters of each component

假设装备在观测周期内的工作时间为400 h，取本文方法、仿真方法和文献[23]中近似法进行对比，求得数值分别对应图3至图8中解析值、仿真值和近似法对应的曲线，对比情况如图3至图8 所示。

图3 方案1不同方法满足率对比情况Fig.3 Comparison of spare parts fill rates of Component 1 by different methods

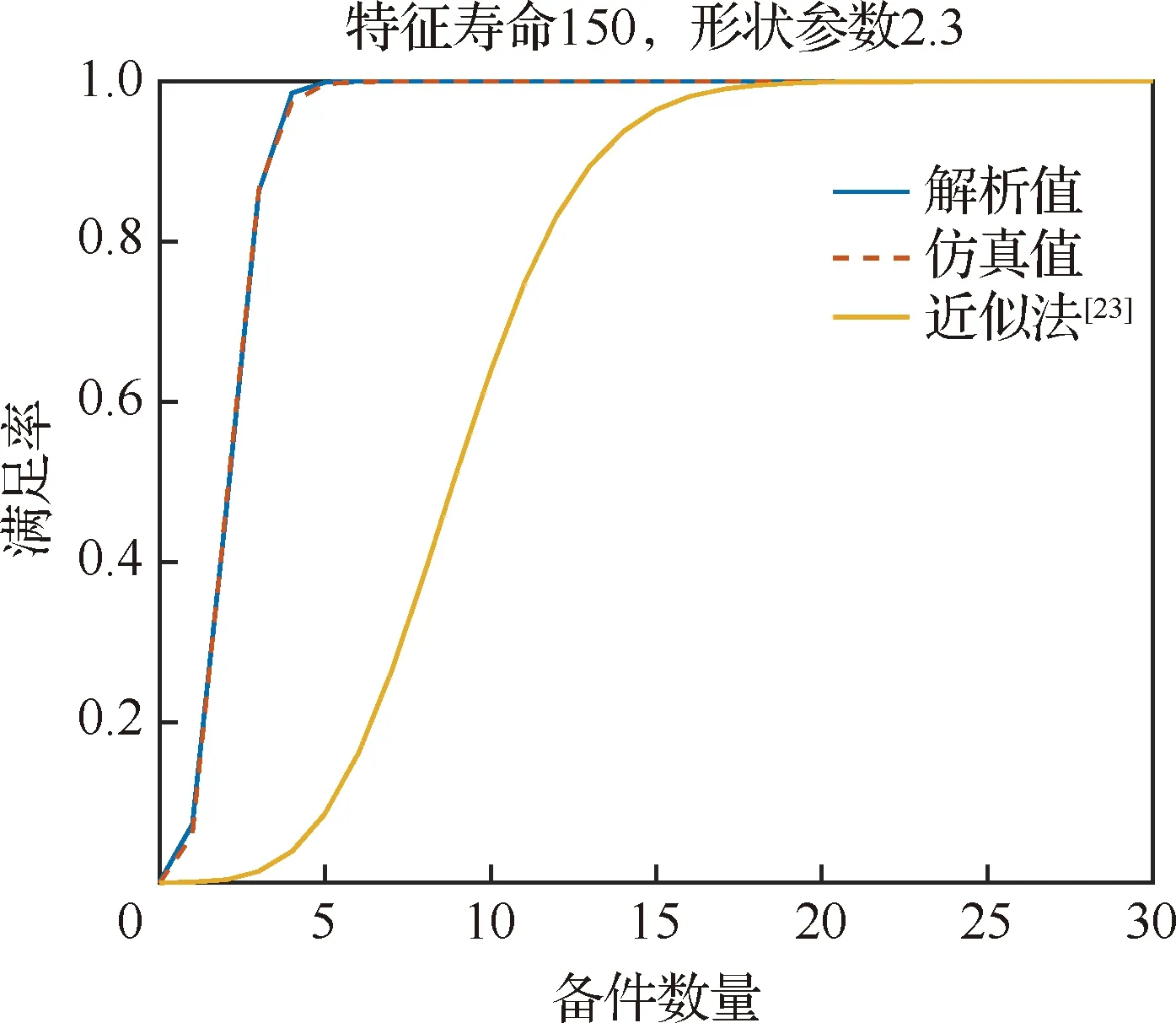
图4 方案2不同方法满足率对比情况Fig.4 Comparison of spare parts fill rates of Component 2 by different methods

图5 方案3不同方法满足率对比情况Fig.5 Comparison of spare parts fill rates of Component 3 by different methods

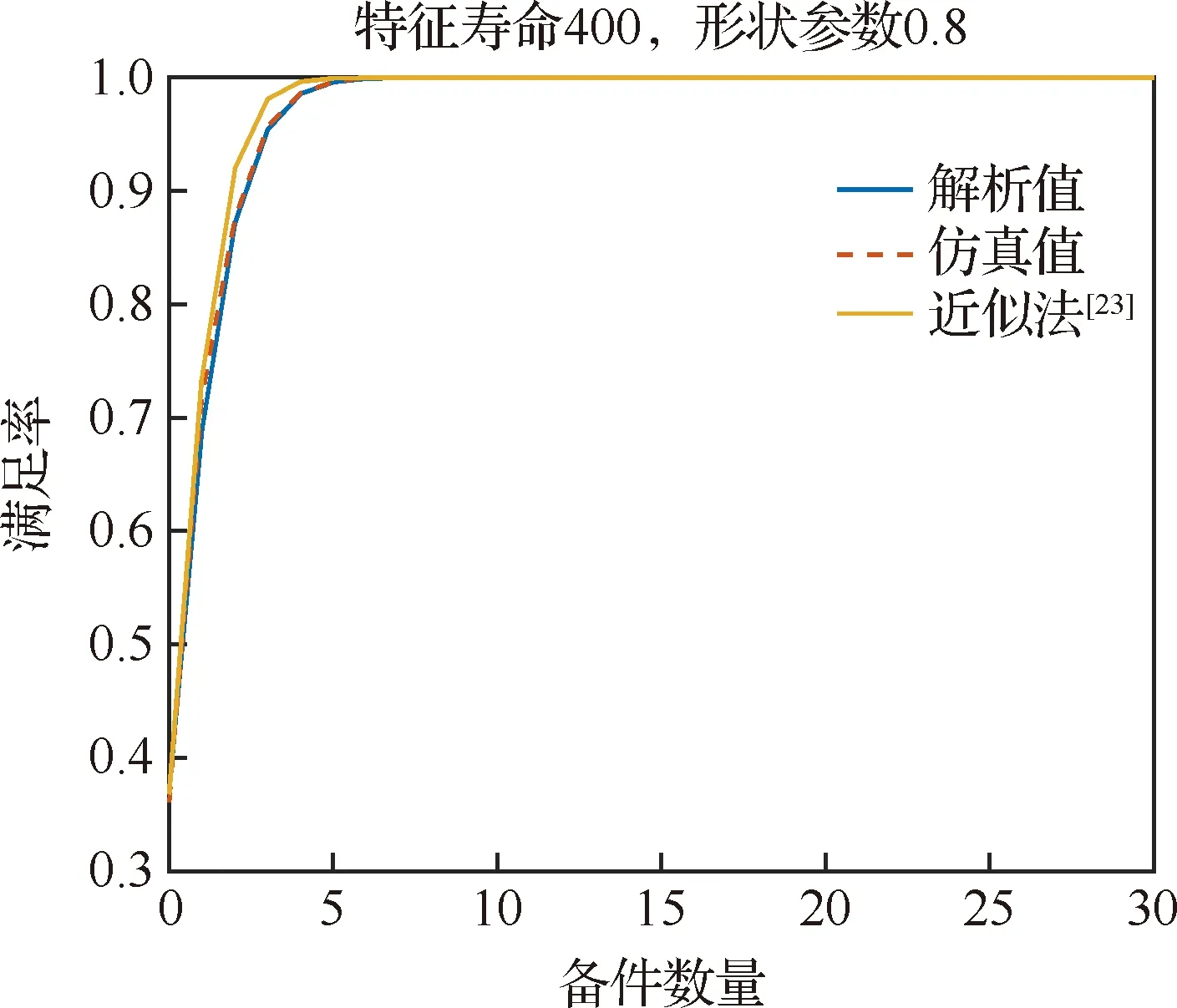
图6 方案4不同方法满足率对比情况Fig.6 Comparison of spare parts fill rates of Component 4 by different methods

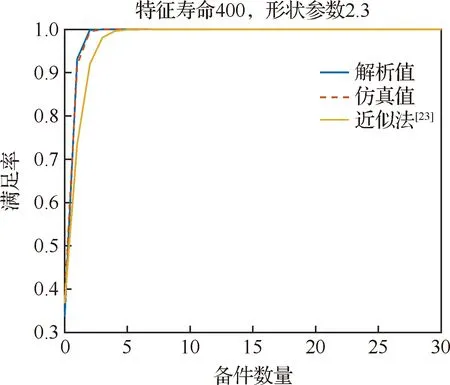
图7 方案5不同方法满足率对比情况Fig.7 Comparison of spare parts fill rates of Component 5 by different methods

图8 方案6不同方法满足率对比情况Fig.8 Comparison of spare parts fill rates of Component 6 by different methods

由图3至图8可知，对于不同寿命分布的威布尔型部件，本文方法求得的备件满足率与仿真结果基本吻合。文献[23]所示方法在威布尔型部件寿命形状参数与特征寿命值之比较小时计算得到的备件满足率与仿真结果较为一致，但误差仍大于本文方法，如图3,图6,图7,图8所示；当形状参数与特征寿命比值较大时，计算得到的备件满足率与仿真结果误差较大，如图4和图5所示。

当各装备工作时间不同时，传统方法难以开展备件满足率相关运算，而本文方法仍具有较强的适用性。假设有5台装备的威布尔型通用件寿命参数如表1所示。在观测期内的工作时间分别为400、500、300、600、800 h。

针对不同寿命分布部件，采用本文所建模型计算威布尔型通用部件的备件满足率随备件数量的变化情况，并与仿真值进行对比，计算结果如图9 至图14所示，观察对比图形可知，对于不同寿命分布的威布尔型通用备件和不同的备件配置数量，本文所建模型均具有较高的评估精度，可为后续开展通用备件配置方案优化打下良好基础。

图9 方案1备件满足率对比情况Fig.9 Comparison of spare parts fill rates of Component 1

图10 方案2备件满足率对比情况Fig.10 Comparison of spare parts fill rates of Component 2

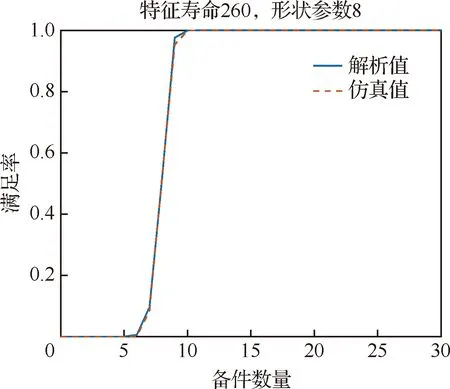
图11 方案3备件满足率对比情况Fig.11 Comparison of spare parts fill rates of Component 3

图12 方案4备件满足率对比情况Fig.12 Comparison of spare parts fill rates of Component 4

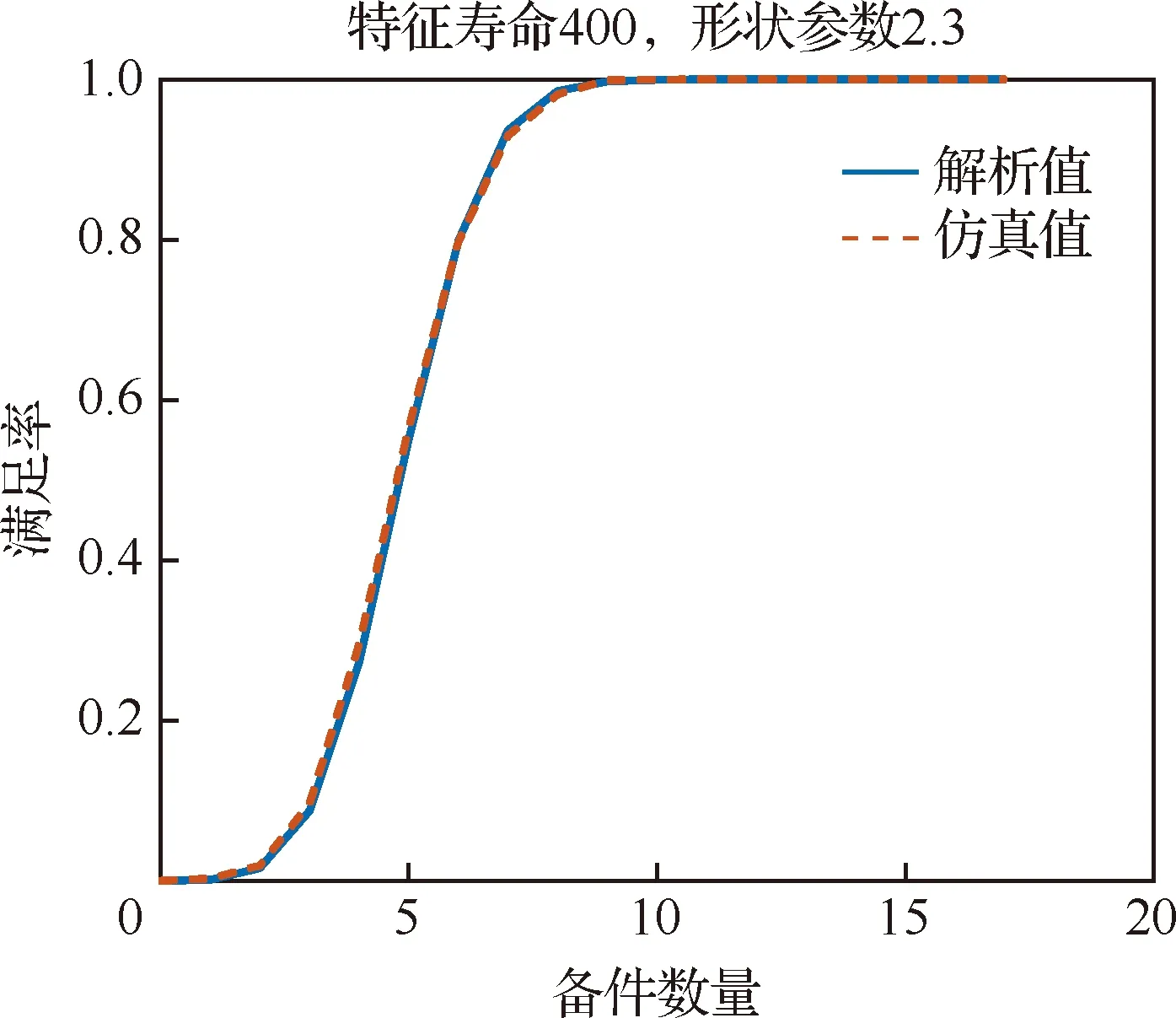
图13 方案5备件满足率对比情况Fig.13 Comparison of spare parts fill rates of Component 5

图14 方案6备件满足率对比情况Fig.14 Comparison of spare parts fill rates of Component 6

5.2 算例分析

假设5台不同类型的装备中都装备有某同一类型通用件，已知该通用件的寿命服从威布尔分布W(240,2.3),根据装备年工作计划，5台装备每年的工作时间分别为400、500、300、600、800 h，某仓库现欲确定该通用件2年的用量，使其备件满足率不低于0.9。

根据第2节描述的威布尔部件备件满足率求解方法与第3节所提备件优化方法求解备件的配置数量，与此同时对备件配置情况进行仿真评估，在备件配置数量的迭代过程中，文中备件满足率计算所得结果与仿真评估结果基本相同，具体对比如表2所示。由该表可知，本文解析方法在备件配置数量较低时，备件满足率较低，二者相差较大，当备件满足率在0.1以下时，二者误差在10%以上，这是由于备件满足率较低时，若此时计算误差比值，分母即仿真值较小，解析值与仿真值之间的误差值对蒙特卡洛仿真值的波动较为敏感，轻微的波动即会带来误差比值的变化，体现出误差较大；随着备件配置数量的增加，装备备件满足率逐渐升高，此时解析方法计算得到的备件满足率与仿真评估结果基本一致，尤其是在备件配置数量达到21个以上时，二者误差基本可以忽略不计。而在实际进行备件配置时，备件满足率较低的方案通常不会采纳，仅会考虑备件满足率在门限值附近或以上的备件配置方案，此时，本文所提方法精度较高，结果可信。

表2 迭代过程中备件满足率计算结果对比

如果在备件满足率指标为0.9的前提下，分别计算各装备独立的备件需求,可得其备件配置数量如表3所示。

将表2和表3数据对比可知，若单独考虑各装备的备件需求而不进行统一考虑时，所需备件数量为每个装备所需备件数量之和为30个；若将各装备作为一个整体，考虑其总的备件满足率，备件数量为26个，这与备件配置过程中的“集聚效应”相一致。也能体现出集中采购通用件在节省备件购置费用的优势。

表3 单个装备备件需求量计算结果

对于不同寿命分布的威布尔型部件，寿命分布如表4所示。5台装备每年计划工作时间分别为400、500、300、600、800 h，仓库现需储存其2年的用量，欲使其备件满足率不低于0.9。采用本文所提方法与仿真方法对比情况如表4所示。

由表4可知，对于不同寿命分布的威布尔通用件，本文备件优化配置方法均具有较强的适用性，计算精度较高，可采用该方法作为工程计算威布尔型部件备件配置数量的方法。

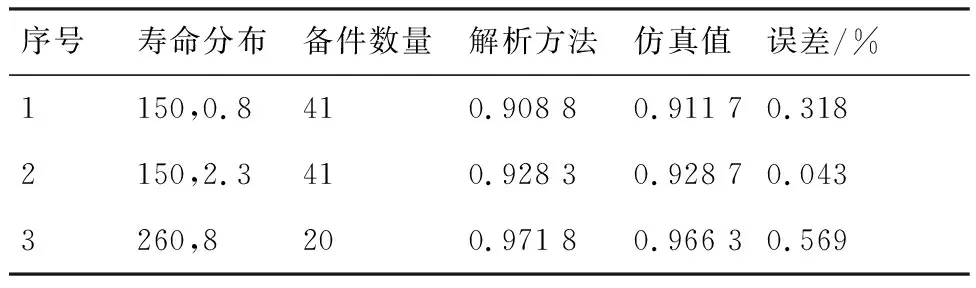
表4 不同寿命分布部件备件优化配置结果对比

6 结 论

1) 针对威布尔型通用件备件满足率评估问题，采用寿命等效原理，将威布尔型备件消耗过程转换为伽玛冲击过程，建立了威布尔型通用备件的满足率评估模型。通过仿真对比分析，本文所建模型对于不同寿命分布的威布尔型通用备件配置方案，均能够准确评估其备件满足率。

2) 在备件满足率指标约束下，给出了备件配置方案优化方法。在备件方案迭代优化过程中，在装备保障部门关注的高备件满足率指标范围内，各备件配置方案所对应的备件满足率均能与仿真值较好贴合，优化后的备件配置方案能够有效满足装备备件需求。整体考虑通用备件的配置情况能够利用备件“集聚效应”减少通用件配置总量，提高备件配置效率。本文威布尔型通用备件配置方案评估及优化方法能够为保障部门评估威布尔型通用备件配置效果，制定配置方案提供决策支持和理论支撑。