复杂时变激励下失谐叶盘瞬态强迫响应分析
敬彤,臧朝平,*,张涛,Yevgen Pavlovich PETROV
1. 南京航空航天大学 能源与动力学院,南京 210016
2. 中国航空发动机集团有限公司 中国燃气涡轮研究院,成都 610500
3. 英国萨塞克斯大学,伦敦 BN1 9RH
叶盘结构,在工作时受到复杂的多谐波激励,具有密集的共振频谱,易产生高周疲劳而损伤[1-2]。众所周知,叶片失谐会导致叶盘结构的幅值放大效应,即失谐叶盘的强迫振动幅值高于其谐调状态[3]。在早期,Slater等[4]对失谐叶盘强迫振动问题做了详细介绍。其后,Krack等[5]用谐波平衡法计算了失谐叶盘在周期、稳态激励下强迫振动和自激振动。段勇亮等[6]提出了一种失谐叶盘减缩建模及动力响应预测方法,可以高效精确地预测失谐叶盘在谐波激励下的稳态响应。然而,大量的发动机试车数据分析指出,在发动机的启动和停车过程中,涡轮叶盘亦表现出较为剧烈的振动问题。因此,在空间谐波成分复杂且具有不确定性特征的发动机阶次激励,以及变转速服役条件所致时变激励条件下,真实涡轮叶盘结构的动力学设计和优化,面临着巨大的挑战。
Dresig和Fidlin[7]首次通过无阻尼单自由度(SDOF)系统分析了具有时变频率成分的复杂激励作用下的瞬态振动响应预测问题。Markert和Seidler[8]利用Faddeeva函数得到了SDOF系统的瞬态振动响应解析解。其后,瞬态响应分析方法逐渐拓展应用于多自由度叶盘系统。此外,Ayers等[9]提出了一种利用模态振动方程的数值积分来预测高加速度下叶盘瞬态振动响应的方法。Yasutomo[10]采用模态叠加法对叶盘等效弹簧质量系统的运动方程进行数值积分求解,对经过共振区的失谐叶盘进行了瞬态振动分析。Hartung和Hackenberg[11-12]通过数值仿真预测了不同行波扫掠速率和阻尼水平下单叶片瞬态振动响应幅值,并通过实验验证了数值仿真结果的正确性。Bonhage等[13-14]提出了一种失谐叶盘瞬态振动响应的半解析求解方法。数值仿真和实验结果表明,失谐叶盘瞬态振动幅值放大因子可能超过稳态振动失谐幅值放大因子。Siewert和Stüer[15]基于时间积分法,将发动机转速变化的离心力的影响通过添加几何刚化矩阵和旋转柔度矩阵实现,对叶片的瞬态强迫响应进行了详细分析,比较了失谐叶盘的瞬态振动响应与稳态振动响应。
涡轮叶盘结构瞬态强迫响应首先要考虑叶盘结构的气动载荷的确定,发动机上游导向器叶片或支板的尾流或下游的势流扰动会引起高阶次激励[16-18](High Engine Order excitation, HEO),这种激励通常会激发叶盘结构的高节径模态。高阶次激励的主要谐波成分一般可以根据叶盘结构前一级静子叶片数目来确定,其实际激发的叶盘耦合振动模态与动/静叶栅中的叶片数有关。而由航空发动机内部结构流动对称性的损失会引发低阶次激励[19-21](Low Engine Order excitation, LEO),这在高压涡轮和低压涡轮中尤为常见。例如,燃烧器出口流场堵塞,燃烧室出口温度不均匀变化以及涡轮导向器叶片喉道宽度变化等均可能诱发形成低阶次激励。低阶次激励的主要特征是变化性和不确定性,这给实验测试带来了巨大困难,这也导致低阶次激励的主要空间谐波成分难以确定。而实际旋转涡轮叶盘所受气动激励是由高阶次激励和低阶次激励组合而成的。多级涡轮上下游导向器产生的高阶次激励,叠加上具有不确定性本质特征的低阶次激励,使得准确预估涡轮叶盘结构在复杂激励下的动态响应变得更为困难。
除了气动载荷空间分布的复杂性外,气动载荷随时间变化的复杂性也是不可避免的。在航空发动机启动和停车的过程中,随着转速升高或降低,旋转叶盘结构将承受加速/减速型行波激励,其激励频率将随转速发生变化。加速/减速型行波激励频率的时变特性取决于发动机的转速控制。这种瞬态激励在旋转涡轮叶盘结构的服役过程中十分常见,但目前仍缺少实际工况下加速/减速型行波激励的实验测试或数值仿真数据。
本文提出了在实际激励载荷下预测失谐叶盘高保真有限元模型位移响应的瞬态振动分析方法。首先,基于传递函数的自由度减缩方法[1],建立了失谐叶盘结构和谐调叶盘结构传递函数之间的关联,并仅选取少量“主节点”进行分析计算,大幅减少了其他从属自由度的计算。其次,考虑复杂的空间谐波成分和变转速下的气动负载,用Tyler-Sofrin激励模型[22-23]来表示包含HEO和LEO的多谐波激励,用3次样条插值的方法来表示各谐波激励频率和幅值随叶盘结构转速的变化函数,同时考虑转速变化对叶片的固有频率和模态特性的影响。最后,通过推导任意时变激励下失谐叶盘瞬态响应的解析表达式,以计算失谐叶盘的瞬态强迫响应。以具有170万自由度以上的涡轮叶盘有限元模型为例,进行了分析验证,比较了单谐激励和复杂激励下的瞬态响应。并结合Campbell图对叶盘共振的转速区间和引起共振的激励阶次成分进行分析,研究了不同阻尼条件下,旋转加速度对失谐叶盘共振响应幅值和失谐幅值放大因子的影响。
1 瞬态响应分析方法
复杂时变激励下失谐叶盘瞬态强迫响应的高效计算分析,涉及到失谐叶盘的减缩建模、叶片表面复杂时变激励的描述、具有不确定性的转速变化历史的数学函数表达、随转速变化的固有频率和振型的描述及瞬态强迫响应的解析表达式等多方面下文将分别探讨。
1.1 失谐叶盘模型减缩方法
受激振力作用的叶盘结构的运动方程可以写成一般形式:

(1)
式中:K=K0+δK,C=C0+δC和M=M0+δM分别是失谐叶盘的刚度矩阵、阻尼矩阵和质量矩阵;它们分别被表示成一个谐调矩阵(如K0)与一个失谐摄动矩阵(如δK)叠加而成。u(t)是随时间变化的叶盘节点位移离散向量:
u(t)=[u1(t),u2(t), …,uN(t)]T
(2)
其中:N为叶盘结构节点总数。外激励矩阵F(t)可以表示为
F(t)=[f1(t),f2(t), …,fN(t)]T
(3)
其中fj(t) (j=1,2,…,N) 是每个节点上的激励。物理位移则可以通过模态振型和模态位移的乘积获得:
u(t)=Φy(t)
(4)
式中:Φ=[φ1,φ2,…,φNm]为模态振型;Nm是减缩模型的模态数量,y(t)=[y1(t),y2(t),…,yNm(t)]T是模态位移。
将式(4)代入式(1)并且左乘ΦT,利用振型的正交性和质量归一化,可以得到关于模态位移的解耦运动方程。因此,第m阶模态自由度的受迫响应为
(5)
式中:ξm和ωm是m阶模态阻尼和固有频率;gm(t)是模态力。
采用参考文献[6]中提出的方法计算叶盘结构的模态特性,基于循环对称特性,利用调谐叶盘单个扇区的有限元模型计算整个调谐叶盘的模态特性,用于创建一个叶盘结构的减缩模型。通过定义特殊的失谐矩阵,模拟实验测量的叶片动力学特性,建立叶片失谐模型。根据这种方法,结构的特征值问题为
(K0+δK)Φ=(M0+δM)ΦΛ
(6)
建立失谐叶盘模态振型Φ和协调叶盘模态振型Φ0的传递函数:
Φ=Φ0cΦ
(7)
式中:cΦ为传递系数矩阵,将式(7)代入式(6)并左乘ΦT重塑失谐结构的特征值问题,得到:
(Λ0+ΦTδKΦ)cΦ=(I+ΦTδMΦ)cΦΛ
(8)
其中:Λ0为谐调叶片盘特征值的对角矩阵。求解这个方程可得到传递系数矩阵cΦ和失谐结构的特征值Λ,之后利用式(7)可求出失谐叶盘的振型。相比于结构的特征值问题式(6),重塑后的特征值问题式(8)的求解显然消耗更少的计算资源。对于瞬态响应分析,可通过解析式(5)求解任意时变载荷下的模态位移响应,再利用这些解和式(4)可计算出叶片任意节点处的物理位移响应。
1.2 随时间变化的模态力计算
外激励的主要来源是叶盘结构经过非均匀流场产生的非定常气动力,该激励分布在叶片表面,其力的幅值及分布情况随转速的变化而变化。Tyler-Sofrin激励模型[22-23]可以用来描述外激励在柱坐标系上的分布。随时间变化的外激励的一般表达式则可以写成如下形式:

(9)

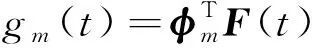
(10)
式中:F(t)为叶盘减缩模型中的所有节点力,通常可以通过CFD计算每一时刻的节点力,并将每一时刻的节点力以式(9)的形式表示。然而,通过CFD计算每一时刻的节点力,所需的计算工作量巨大,这样计算外激励就需要花费大量时间。因此,本文对激振力进行了适当简化,假设叶片上的激振力分布随转速的变化而变化,外激励沿周向以傅里叶级数展开:

(11)
式中:ω(t)为叶盘转速,在感兴趣的转速范围内,模态力可表示为
(12)

k=1,2,…,Nω-1
(13)

1.3 转速变化历史描述
转速随时间的变化历史是由飞行员在飞行过程中对燃气轮机的操作决定的。转速在发动机加速过程中增大,在减速过程中减小。函数在实际情况下转速变化是复杂的,假设它是已知的并使用分段线性函数近似,如图1所示。图中共NT个时间区间,在第k个时间区间[tk,tk+1]内,随时间变化的转速可以表示为
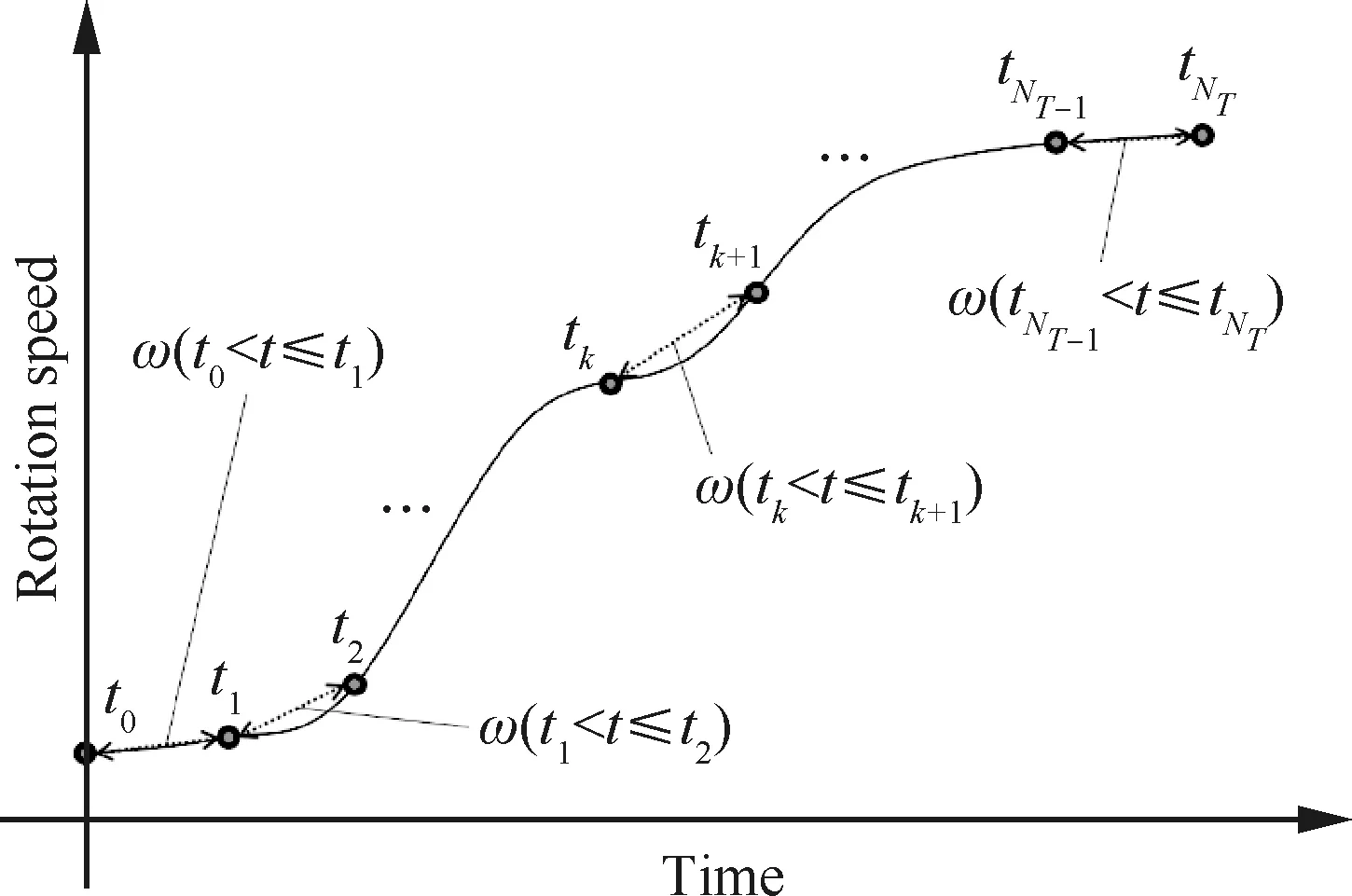
图1 转速随时间变化的描述方法Fig.1 Approximation of rotation speed varying with time
ω=ω(tk)+αk(t-tk)
(14)
式中:ω(tk)为时间tk处的转速;αk为旋转角加速度,在时间区间[tk,tk+1]内为常数。
描述叶盘转动引起的激振力相位变化的函数,θ(t),可用如下形式计算得到:
(15)
式中:θ(tk)为时间tk处的相位角,可以通过对t0到tk时间历史上的转速进行积分获得:
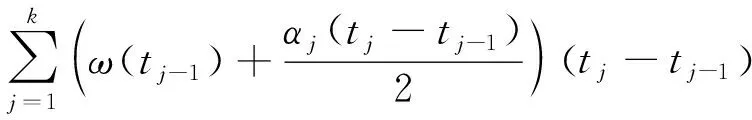
(16)
1.4 随转速变化的模态特性
刚度矩阵包括描述离心力刚化效应下的几何刚化矩阵和由于离心力方向改变影响的旋转软化矩阵,它随转速的变化而变化。对于失谐叶盘的模态振型φm(ω)和固有频率ωm(ω)也均与转速有关。在关心的转速变化范围内,通过计算若干转速下叶片的振型和固有频率,可以确定模态特性和转速的关系。
参考转速的个数取决于模态特性对转速的灵敏度,通常可以选取 2~8个转速点,使用三次样条多项式近似描述转速与固有频率、模态振型的函数关系,从而可计算出任何转速和时间下的模态参数:
ωm(ω(tk)<ω(t)≤ω(tk+1))=
(17)
φm(ω(tk)<ω(t)≤ω(tk+1))=
(18)

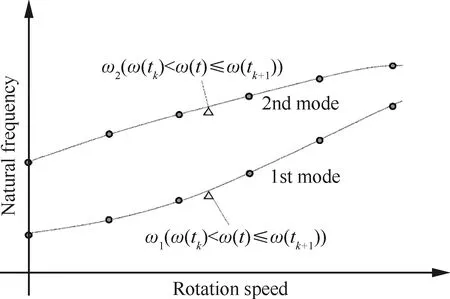
图2 固有频率随转速变化的描述方法Fig.2 Approximation of natural frequencies varying with rotation speed
1.5 瞬态响应的计算方法
运用初始条件,受激励的单自由度系统的微分方程式(5)在每个模态坐标下的位移和速度响应可以通过杜哈梅积分(Duhamel’s integral)进行求解:
(19)
(20)
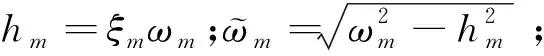
(21)
(22)
(23)
(24)
其中几个积分函数如下所示:
(25)
(26)
在积分求解时,假定在区间[tk,tk+1]内的转速随时间线性变化,并利用式(15)进行计算。此外,在此极小的时间区间内,假定固有频率和模态振型为常数,并利用式(17)和式(18)给出的三次样条多项式来计算。完成对系统的模态参数和模态力相位的数学描述后,可以推导出积分式(25) 和式(26)的解析表达式:
(27)
(28)
(29)
(30)
其中的一些参数如下所示:
(31)
(32)
(33)
w(-iz±(tk)))
(34)
(35)
其中:w(x)为Faddeeva函数[24],可以表示为
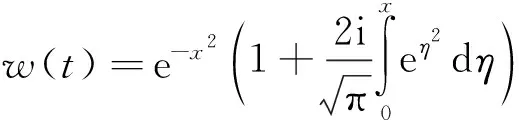
(36)

2 数值分析与讨论
2.1 精度分析
为了评估本文方法的误差和合理性,本文以成熟地用于求解非线性常微分方程的Runge-Kutta法作为参考,虽然该方法在计算大规模有限元模型时缺乏经济性,但在模型规模较小时具有精度高和易使用的优点。因此,本文采用一个简单的2自由度集总质量模型来分析新方法的精度,如图3所示。该结构的质量(m1=4和m2=2)和阻尼(c1=0.4和c2=0.2)为不随时间变化的常数,刚度随转速发生变化。弹簧k1随转速升高而减小,用来模拟结构旋转软化效应;弹簧k2随转速升高而减小,用来模拟结构的应力刚化效应,如图4所示。
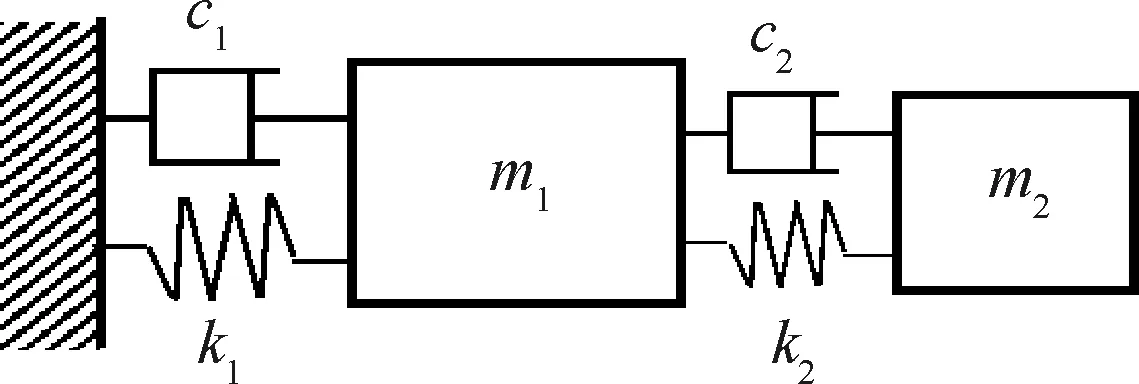
图3 2自由度的集总参数模型Fig.3 Lumped parameter model of 2 degrees of freedom
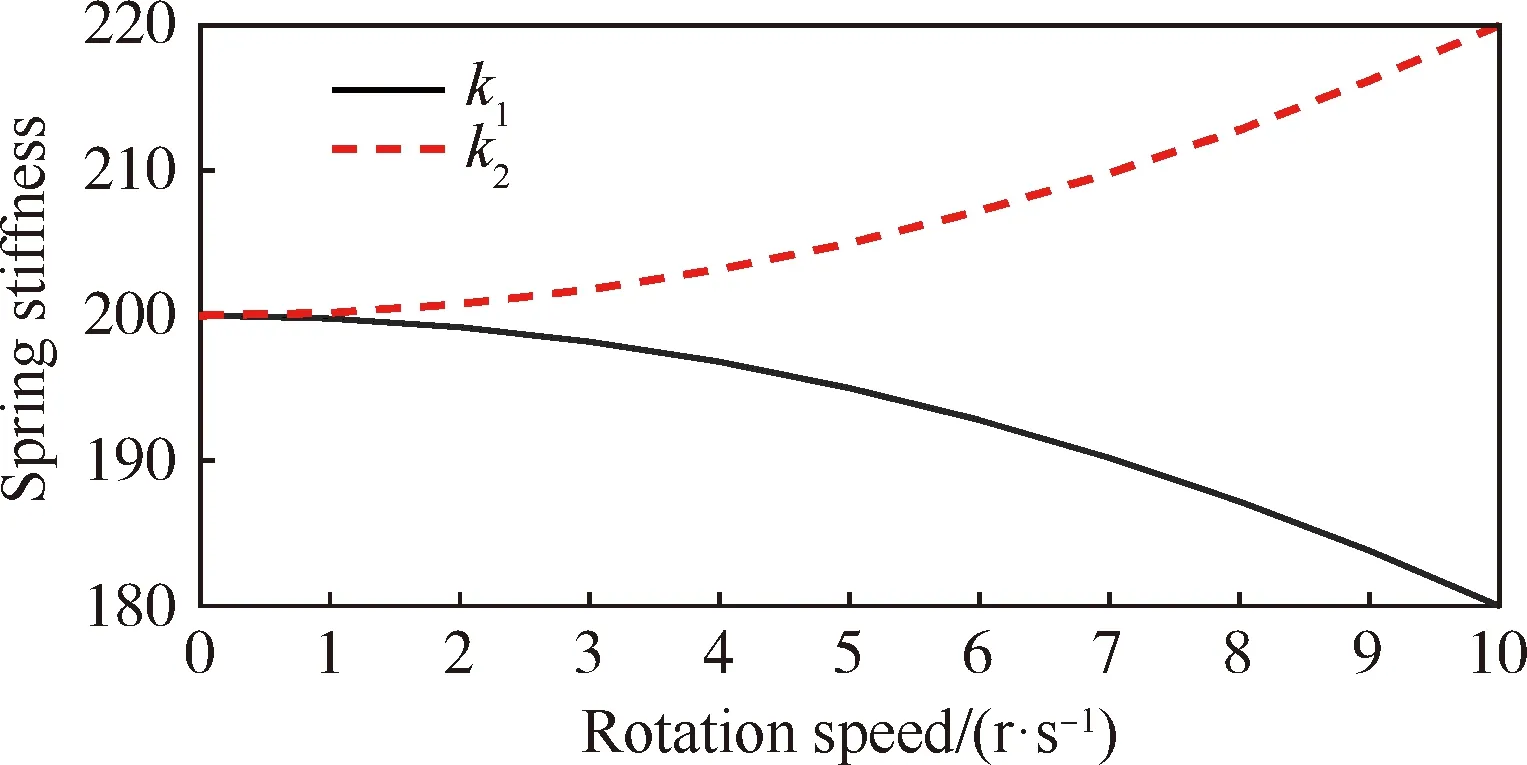
图4 随转速变化的弹簧刚度Fig.4 Spring stiffness varying with rotational speed
首先,分别在转速为0、2.5 r/s,5 r/s,7.5 r/s和10 r/s共计5处计算系统的模态参数,利用三次样条函数来描述转速对频率和振型的影响。其次,在质量m2上施加频率为2倍转速的加速行波激励。最后,使用本文提出的新方法求解2自由度系统的瞬态位移响应,并与相同外激励下Runge-Kutta法计算的瞬态响应进行对比,如图5所示。局部放大观察发现,新方法的响应计算结果与Runge-Kutta法的计算结果基本相同。它们之间的相对误差,最大误差不超过0.14%,如图6所示。

图5 两种方法下的瞬态响应Fig.5 Transient responses in both methods
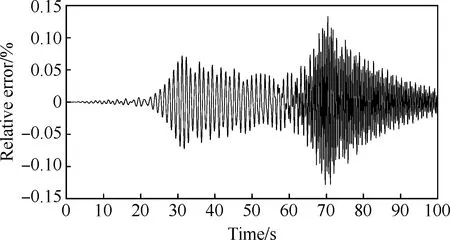
图6 两种方法下瞬态响应的相对误差Fig.6 Relative error of transient responses in both methods
在新方法中使用三次样条近似是误差的主要来源,尤其是为了减少模态分析的次数在较大的转速区间只使用5个转速点的模态参数来拟合时变的模态参数。取点不足导致较大误差,采用更多的点来构建三次样条函数可以提高该方法的精度。计算不同插值点数目下新方法与Runge-Kutta法的相对误差,如图7所示。结果表明,随着插值点数目从5个增加到2 000个,响应计算误差从0.14%减小至10-6%。因此,可以根据使用者对精度和经济性的需求来选择插值点的数目。

图7 相对误差随插值点数目的变化Fig.7 Relative error varying with purpose of interpolation points
2.2 涡轮叶盘
本文的计算模型为有86个叶片的某涡轮叶盘,其有限元模型如图8所示,图8(a)为叶盘整体模型,图8(b)为单个扇区模型。以10节点187单元划分网格,单个叶片共56 982个节点、31 062个单元。叶盘材料弹性模量为210 GPa,密度为7 800 kg/m3,泊松比为0.3。在数值分析中,假设叶片根部与盘之间固支连接,失谐叶盘的结构和气动能量耗散效应使用模态阻尼比来表征,模态阻尼比假设默认为0.001,如果使用其他阻尼因子值(例如0.003和0.01),则在文中指出。

图8 涡轮叶盘Fig.8 Turbine bladed disk analysed
首先,基于谐调叶盘的循环对称特性,通过单个扇区的有限元模型得到谐调叶盘的固有频率和相对应的模态振型,谐调叶盘的固有频率与节径的关系如图9所示。考虑叶盘不同节径下的前10阶固有模态,叶盘的节径从0变化到43,计算了叶片前860个固有频率和振型,并用于瞬态力响应分析。根据模态特性与转速的关系,对均匀分布在0~200 r/s频率范围内的5种转速进行模态分析。为了不显著增加计算消耗,着重计算叶片尖端的瞬态位移。

图9 调谐叶盘的固有频率Fig.9 Natural frequencies of tuned bladed disk
其次,将分布在叶片表面的质量附加到叶片上,使单个叶片一阶固有频率在±5%范围内发生偏移,从而模拟叶片的失谐。用于模拟叶片表面的失谐质量节点均匀分布在叶片表面的所有节点上。失谐排布采用随机形式,使叶盘所有叶片发生不同程度的频率偏移,如图10所示。
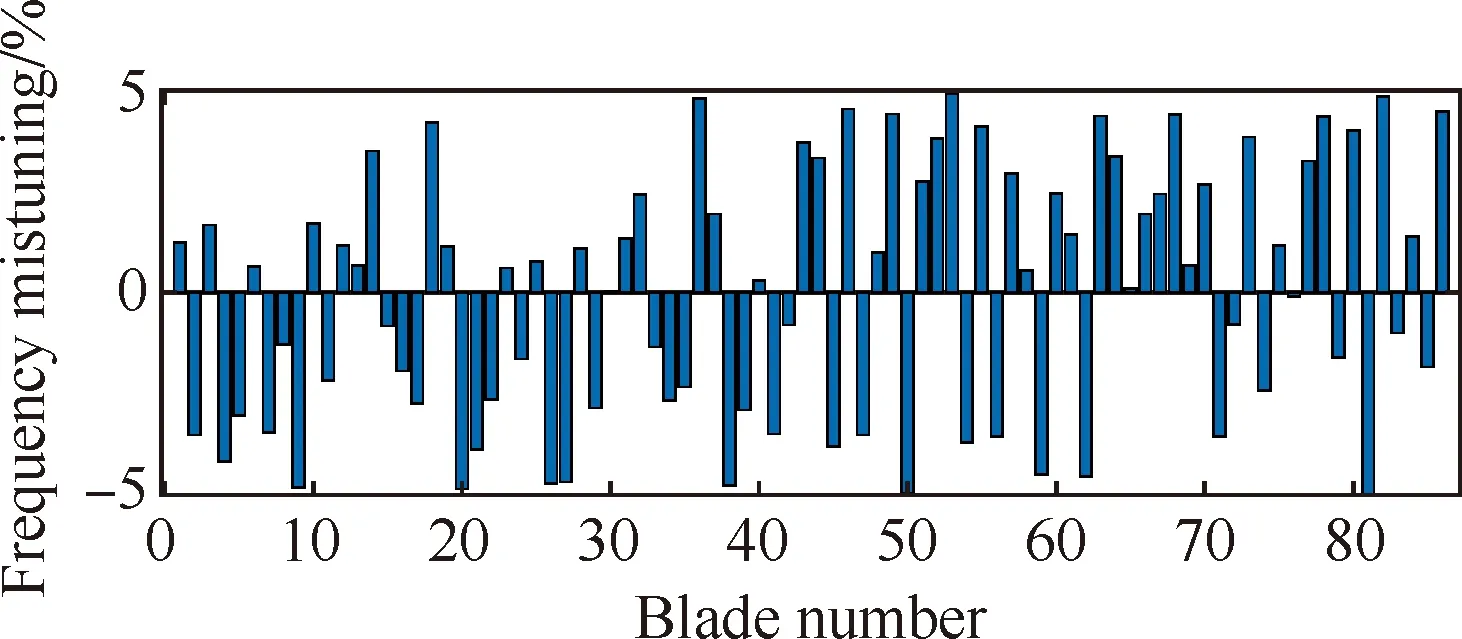
图10 随机产生的叶片失谐排布形式Fig.10 Randomly generated blade mistuning pattern
2.3 复杂激励
叶盘结构叶片上真实且复杂的非定常气动载荷的分布,采用参考文献[21]中的气体流动计算数据进行模拟,为了方便描述叶片表面气动载荷沿叶型分布的函数,根据不同弦长和叶高上的位置建立坐标系,如图11所示。
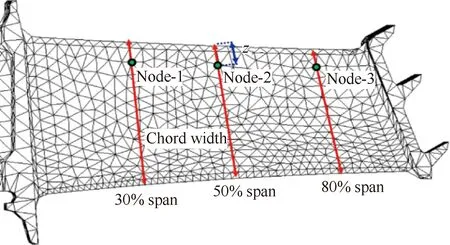
图11 叶片表面不同弦长和叶高上的位置Fig.11 Positions on different chords and spans of blade surface
不同叶高处的表面压力幅值沿叶型弦长方向变化实例如图12所示。3个不同叶高的例子在图中展示,它们分别是30%叶高处,50%叶高处和80%叶高处。用三次样条拟合来描述这种压力幅值的变化。

图12 叶片表面不同弦长和叶高上的非定常激振力分布Fig.12 Unsteady excitation force distribution on different chords and spans of blade surface
在不同的叶高位于弦长20%处选取的3个节点。叶盘旋转一周,3个节点上随所承受的气动载荷如图13(a)所示。不同节点上的气动载荷都有所不同,这些载荷的谐波组成如图13(b)所示。在叶盘前方静子叶栅数量为24时,高阶次激励(HEO)包含:24EO、48EO、72EO、96EO、120 EO、144 EO、168 EO和192 EO等,分别是是转子叶盘前方静子叶片扰动产生的1~8阶谐波。低阶次激励(LEO)包含:2EO、4EO、6EO、8EO和10EO,它们通常是由一些不确定因素产生。基于Tyler-Sofrin模型,将叶片表面上每一个节点的激励都表示为多个幅值随空间坐标和时间变化的加速/减速行波激励的线性叠加。之后,将节点力转化为模态力施加在减缩模型上进行计算。

图13 分叶片表面单节点(1,2,3)非定常激励力Fig.13 Unsteady excitation force on one node (1, 2, 3) of blade surface
2.4 共振转速的确定
考虑转速对固有频率的影响,共振频率是根据Campbell图确定的。图14(a)给出了0到200 r/s 的转速范围内,24节径振型模态族的固有频率随转速的变化的Campbell图。本文重点研究45 r/s到70 r/s转速范围内的共振点,同时此范围将被用于瞬态响应分析。可以看到在转速范围45~70 r/s内有一个共振点由24EO激发,该模态为24节径模态族的第1阶模态。图14(b)展示了38节径模态族的固有频率,给定的激励阶次中只有48EO能激起该节径模态,如图所示在转速范围45~70 r/s内一个共振点被激发(第4阶模态)。图14 (c)展示的则是10节径振型模态族的固有频率,给定的激励阶次中只有10EO和96EO能激起该节径模态,其中96EO激发一个共振点(第4阶模态),而10EO没有激发共振。

图14 转速对固有频率和共振的影响Fig.14 Effect of rotation speed on natural frequencies and resonances
2.5 简谐和复杂激励下的瞬态强迫响应
各谐波单独激励和整体复杂激励下的谐调叶盘瞬态响应如图15 (a)所示。此时阻尼比为0.001,旋转加速度为1 r/s2。通过调谐叶片圆盘
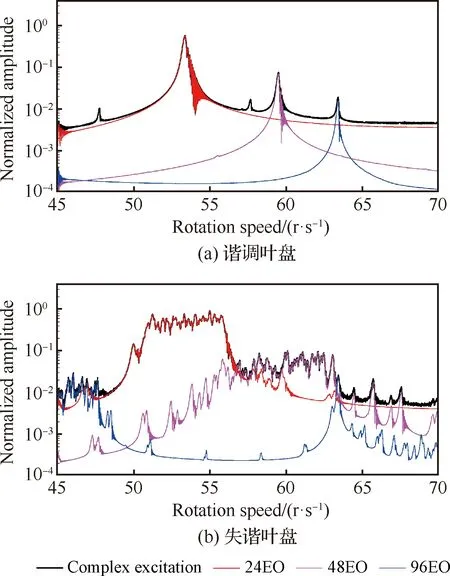
图15 旋转加速度1 r/s2下的瞬态响应Fig.15 Transient responses under rotation speed acceleration 1 r/s2
稳态强迫响应最大振幅值,对叶盘响应振幅进行归一化。由24EO激发的第1模态的共振峰达到最高响应水平,其归一化幅值约为0.6,远远高于由48EO激发的第2模态(0.08)和96EO激起的第4模态(0.02)。对于相同激励条件下的失谐如图15 (b)所示,由24EO激发的第1模态的共振峰达到最高响应水平,其归一化幅值约为1,远远高于由48EO激发的第2模态(0.1)和96EO激起的第4模态(0.03)。
转速加速度10 r/s2时的瞬态响应如图16 (a)所示。由24EO激发的第1模态的共振峰达到最高响应水平,其归一化幅值约为0.3,远远高于由48EO激发的第2模态(0.03)和96EO激起的第4模态(0.01)。对于相同激励条件下的失谐如图16 (b)所示,由24EO激发的第1模态的共振峰达到最高响应水平,其归一化幅值约为0.4,远远高于由48EO激发的第2模态(0.06)和96EO激起的第4模态(0.02)。
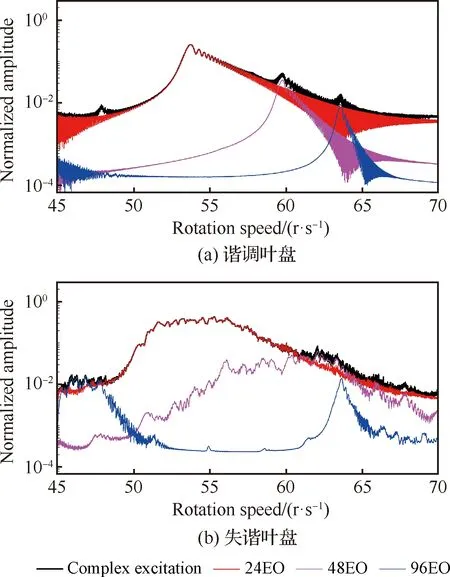
图16 旋转加速度10 r/s2下的瞬态响应Fig.16 Transient responses under rotation speed acceleration 10 r/s2
2.6 阻尼和旋转加速度对瞬态强迫响应的影响
考虑阻尼比值分别为0.001、0.003和0.01,旋转加速度分别为1 r/s2和10 r/s2时,对叶盘结构瞬态响应进行预测,并与稳态振动情况下的响应进行了比较。当阻尼比取0.001时,谐调叶盘的瞬态和稳态响应的对比如图17(a)所示。谐调叶盘的稳态振动的归一化振幅为1,对叶盘响应振幅归一化后可以看出,随着旋转加速度增加到10 r/s2,归一化瞬态振幅明显减小为0.25。最大瞬态响应所在的转速相较于稳态最大响应从53 r/s 偏移至54 r/s。失谐叶盘的瞬态和稳态响应如图17(b)所示。当阻尼比取0.003时,谐调叶盘的瞬态和稳态响应的对比如图18(a)所示。随着旋转加速度增加到10 r/s2,归一化瞬态振幅相对于稳态振幅减小为0.6。失谐叶盘的瞬态和稳态响应如图18(b)所示。当阻尼比提高到0.01,谐调叶盘的瞬态和稳态响应如图19(a)所示。随着旋转加速度增加到10 r/s2,归一化瞬态振幅仅仅减小10%。失谐叶盘的瞬态和稳态响应如图19(b)所示。

图17 阻尼比0.001下的归一化振幅Fig.17 Normalized amplitude with damping ratio of 0.001
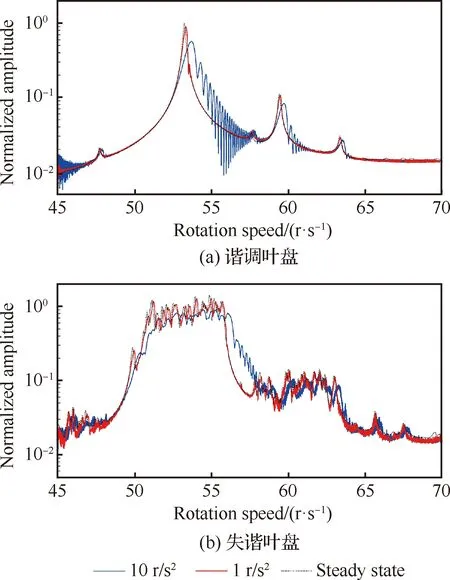
图18 阻尼比0.003下归一化振幅Fig.18 Normalized amplitude with damping ratio of 0.003

图19 阻尼比0.01下归一化振幅Fig.19 Normalized amplitude with damping ratio of 0.01
图20比较了不同阻尼下,大范围旋转加速度对瞬态响应幅值的影响。可以看到当旋转加速度小于某一数值时,瞬态响应接近于稳态响应,超过这一数值到更高的加速度过程中,归一化振幅则显著减小。阻尼比为0.001时,当旋转加速度从0.03 r/s2增加到10 r/s2过程中,失谐叶盘的归一化振幅从1.27减小到0.4,降低了68%左右。
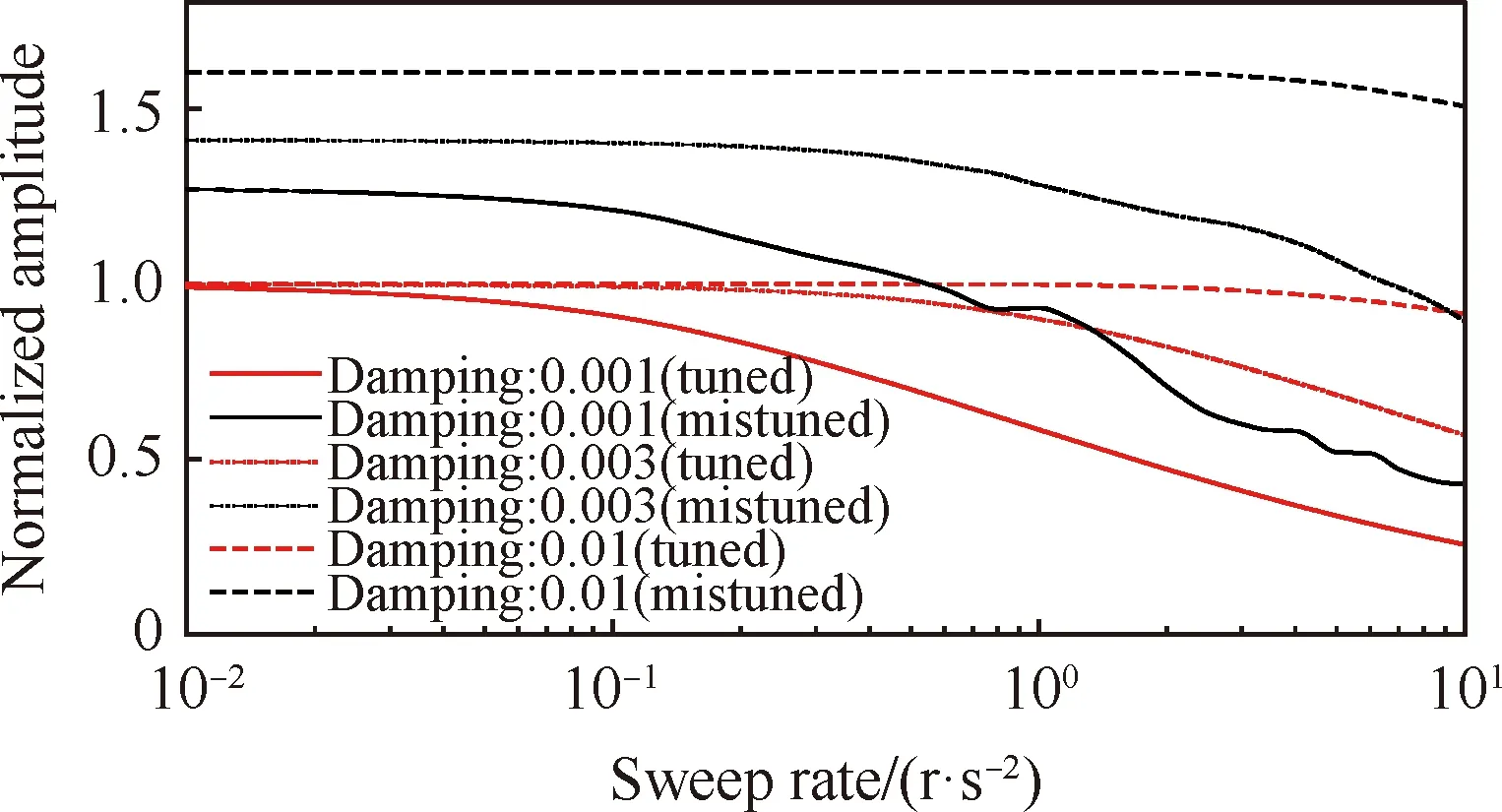
图20 在转速范围为46 r/s到60 r/s的高转速下归一化最大振幅Fig.20 Normalized maximum amplitudes in high rotation speed in rotation speed range from 46 r/s to 60 r/s
阻尼比为0.003时,当旋转加速度从0.3 r/s2增加到10 r/s2过程中,失谐叶盘的归一化振幅从1.4减小到0.9。阻尼比为0.01时,当旋转加速度从3 r/s2增加到10 r/s2过程中,失谐叶盘的归一化振幅仅从1.6减小到1.5。在低阻尼的情况下,归一化振幅随转速加速度的增大而减小更为显著。
失谐振幅放大因子,即失谐叶盘与谐调叶盘的最大振幅的比值,随旋转加速度的变化如图21所示。引入瞬态振幅放大因子与稳态响应分析中常使用的放大因子做类比,用于研究不同瞬态条件对失谐叶盘振动特性的影响。可以观察到,叶盘的失谐幅值放大因子在瞬态条件下大于稳态条件下。在阻尼比为0.001时,瞬态振幅放大因子最大值达到1.67,而稳态响应为1.28,增幅超过30%。阻尼比增大为0.003时,瞬态振幅放大因子最大值达到1.58,而稳态响应为1.41,增幅超过12%。阻尼比最大取0.01时,瞬态振幅放大因子最大值达到1.65,而稳态响应为1.60,增幅仅为3%。

图21 转速范围为46 r/s~60 r/s的瞬态振幅放大系数Fig.21 Transient amplitude amplification factor in rotation speed range from 46 r/s to 60 r/s
3 结 论
本文提出了一种高效的失谐叶盘瞬态强迫响应分析方法。针对实际工业尺寸的叶盘高保真有限元模型,通过叶盘的模型减缩,极大地减少了自由度数目,同时可精确地描述失谐叶盘结构的动力学特性;采用Tyler-Sofrin激励模型和三次样条近似方法,用简单的数学函数描述了叶盘变转速工况条件下分布在叶片表面节点上的气动激励和模态特性;将失谐叶盘位移响应在模态坐标下的展开,推导出任意时变激励下失谐叶盘的瞬态强迫响应解析式,从而,避免了耗时的积分运算,大幅提高了响应预测的效率。
以某86个叶片的涡轮叶盘为例,通过共振分析确定了叶盘共振的转速区间和引起共振的激励阶次成分。分别计算了叶盘加速旋转时,单谐波激励和复杂多谐波激励下谐调和失谐涡轮叶盘的瞬态响应。对比分析发现,复杂激励中引起共振峰的激励阶次成分与共振分析的结果一致。
计算了不同阻尼条件下的叶盘结构在不同旋转加速度下的瞬态强迫响应。分析了稳态强迫响应和不同旋转加速度下失谐叶盘响应幅值放大因子的变化。结果表明,相同阻尼条件下,失谐叶盘的瞬态强迫响应幅值随旋转加速度升高而降低最多可达68%,但同时其失谐幅值放大因子随旋转加速度升高而增加,增幅超过30%。

