基于刚度损伤的钢框架结构IDA 抗震倒塌方法研究
薛 辰, 田石柱
(苏州科技大学 土木工程学院,江苏 苏州 215011)
逐步增量动力分析方法(IDA)自1977 年问世以来,经过学者进一步的分析总结推广,将IDA 方法应用于基于性能的地震工程,形成一套具有实用性、完整体系化的抗震分析理论,已被美国联邦紧急管理(FEMA)归纳采用[1-2]。该方法可以反映不同地震动强度作用下结构的抗震性能,是一种非常实用的结构抗倒塌能力的评估方法。
IDA 分析中,如何合理地选择地震动强度水平IM 和结构损伤指标DM 是一大问题。Vamvatsikos 将PGA与阻尼比为5%的一阶周期谱加速度Sa(T1,5%)分别作为IM 进行IDA 分析比较,发现后者离散性更小[3]。 叶列平对33 个地震动强度指标进行研究,认为地震动峰值速度和一阶周期谱加速度作为地震动强度指标较为理想[4]。 于晓辉从有效性、充分性、实用性、有益性及结构鲁棒性等五个方面对60 个地震动强度指标和6 个结构损伤指标进行概率评价,结果表明,结构谱加速度和层间位移角作为分析指标能基本描述地震动强度与结构反应之间的概率统计关系[5]。 杨坤对基于层间位移角和残余位移角的IDA 方法进行统计归纳,认为残余位移角作为IDA 损伤指标偏于保守[6]。
与IDA 方法相比, 基于刚度的倒塌判定准则提出得较早但发展较慢。 刚度准则中的破损指数最早由Sozen 提出,Banon、Roufaiel 和Meyer 分别在此基础上对刚度破损指数的定义进行改进, 提出了不同的刚度损伤模型[7-9]。 杜修力则以退化刚度比作为破损参数来判定结构倒塌,张松柏认为以刚度作为结构的倒塌判定方法低估了结构的损伤[10-11]。 按照该方法,结构较难达到倒塌临界点的损伤值。
为了解决上述问题,本文结合刚度倒塌判定准则和增量动力分析(IDA)方法,提出以层间构件刚度损伤Di和结构整体刚度损伤DT作为结构损伤指标的IDA 抗震倒塌判定准则。 采用OpenSees 有限元分析软件,以结构一阶周期谱加速度Sa(T1,5%)作为地震动强度IM,对钢框架结构做不同损伤指标DM 的IDA 分析,对结构抗震倒塌判定方法进行对比评估。
1 基本方法
为了契合钢结构的刚度特性,改进了构件刚度损伤模型[8-10],即

式中,K0是构件的初始弹性刚度 (构件屈服弯矩M0与屈服曲率φ0的比值);Km是构件在地震作用下最大曲率φmax对应的割线刚度;Kf是极限强度对应的割线刚度(构件极限弯矩Mf与极限曲率φf的比值),详见图1。
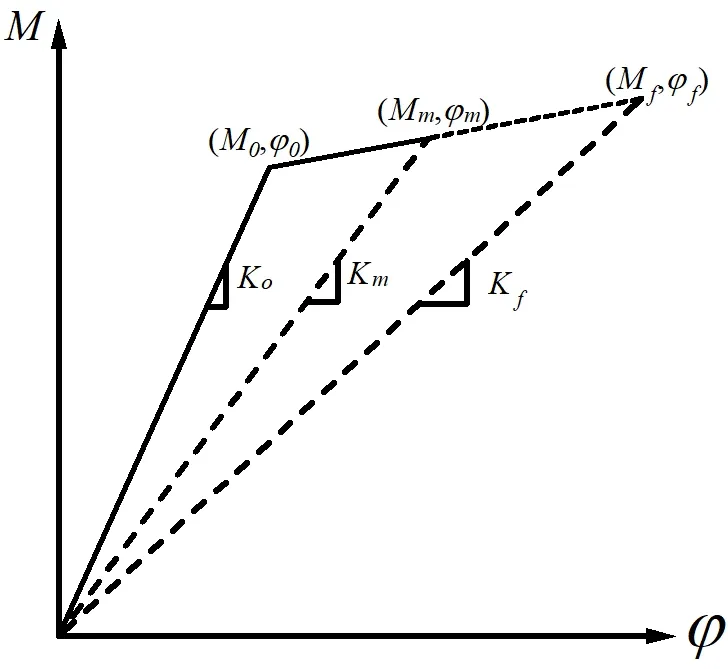
图1 刚度参数设计示意图
结构中部梁柱较外部承受荷载大,往往震后损伤较为严重,因此以梁柱的位置及重要性进行加权。 在得出构件端部塑性铰刚度损伤Dk后,用如下方法得到各层的刚度损伤之和Di。

其中,n 为第i 层形成塑性铰数目,等于第i 层构件数目的两倍;β 为梁柱侧重系数,中部梁柱及重要构件取值为1.2,边柱外梁及非重要构件取值为1。
再根据楼层的参与度,对各层构件损伤进行加权,得到结构整体的刚度损伤指标DT。

式中,wj为加权因子;Ds为各层破坏指数;N 为楼层数。
以结构谱加速度Sa(T1,5%)作为地震动强度指标IM,分别以第i 层构件刚度损伤总和Di和结构整体刚度损伤DT作为损伤指标DM,得出结构的IDA 曲线簇。
2 计算模型
2.1 分析模型
研究运用PKPM 设计7 层内廊式钢框架结构,底层高4.2 m,其余标准层均为3.4 m,尺寸详见图2。该结构按照Ⅱ类场地、7 度(0.10g)设防烈度、第二设计地震分组、三级抗震等级设计,满足抗震设计规范要求。 设计楼板为混凝土楼板,厚100 mm。 按《建筑结构荷载规范》(GB 50009-2012)要求,楼面恒载设为4.5 kN/m2,楼面活载为2 kN/m2,走廊活荷载为3.5 kN/m2,且不考虑风荷载。

图2 模型结构图
采用OpenSees 软件对中间榀框架(图2(a)中阴影部分)进行有限元建模分析。 梁柱构件均采用Q235 的H 型钢,所有梁均采用HN400 mm×200 mm×8 mm×13 mm,第1 至3 层柱选用HW400 mm×400 mm×13 mm×21 mm,第4 至7 层柱为HW350 mm×350 mm×12 mm×19 mm。所有梁柱节点连接和柱脚连接均为刚结。选用材料模型为考虑应变硬化影响的Steel02,采用Fiber 纤维截面,梁柱均采用基于刚度的弹塑性纤维单元Disp Beamcolumn,阻尼比取0.05,考虑P-Δ 效应。
结构前五阶自振周期、自振频率如下表1 所列。

表1 结构模态
2.2 地震波选取及调幅
从Peer 官网获取满足结构设计反应谱的10 条地震波,各地震波数据如下表2 所列,各地震动的加速度反应谱如图3 所示。

表2 地震记录表

图3 地震反应谱曲线
将表2 所列的10 条地震波按Hunt&Fill 调幅方法分别进行不等步调幅,以谱加速度0.005 g 作为初始IDA 弹塑性时程分析,逐步增大谱加速度,得到各结构损伤指标下的IDA 曲线。 当IDA 曲线斜率下降至初始斜率的20%时, 此时的谱加速度作为结构的倒塌极限临界点,并对倒塌极限状态点处的谱加速度做对比分析。
2.3 参数确定
通过对梁、 柱构件做Pushover 得出构件的屈服弯矩与屈服曲率,用两者比值作为弹性刚度K0, 并取极限强度的75%所对应的原点刚度作为极限刚度Kf,具体参数如下表3 所列。

表3 各构件刚度参数表
3 基于刚度损伤指标的IDA 分析
选取IM 为阻尼比5%的谱加速度Sa(T1,5%),以层间构件刚度损伤Di、结构总损伤DT作为DM,绘制10条地震动下的IDA 曲线。
3.1 基于构件刚度损伤指标的IDA 分析
由于结构在较低地震动强度下处于弹性阶段,其构件端部未形成塑性铰,其弯矩-曲率曲线趋于一条直线,构件损伤均趋于零。 故在结构最大层间位移角达到1/200 时,开始记录层间构件刚度损伤Di的IDA 曲线。 图4 所示为10 条地震记录下结构各层构件损伤和IDA 变化曲线图。

图4 Sa(T1,5%)-Di 曲线图
由图4 可以看出随着地震动强度不断增大, 整体层间构件刚度损伤不断加大,IDA 曲线斜率逐渐变缓(见图4(i)),倒塌点十分明显。但在部分地震动作用下,IDA 曲线并未随着普遍认知的结构抗震特性发展,有短暂的斜率突然变大(见图4(b))或损伤指标Di值大幅度变小(见图4(d))的情况,应力硬化,结构出现“复活”现象。 随着楼层数越来越高,“复活”现象明显程度在不断降低。 尤其在RSN864 波作用下,结构“复活”现象格外明显。从部分地震波影响下结构出现“复活”现象,可以推断出该现象与地震动有很大关系。“复活”现象的产生最直接原因是地震动在不同频段内地震能量分布密度不均匀,具有非平稳的特性,使得地震动频谱特性与结构振动频率相耦合,抵消一部分地震能量。 故地震动强度变大,结构变得有一定韧性,结构突然强化避免倒塌破坏。
构件刚度损伤主要集中在1~3 层,2、3 层IDA 曲线十分接近,也代表这两层破坏程度相当。 部分地震波下4 层IDA 曲线斜率也达到初始斜率的20%,各层间IDA 曲线走向趋势大致相同。 结构最严重损伤破坏出现在1 层,结构出现底部破坏倒塌。 顶部5~7 层的Di值变化不大,受地震影响损伤较小。
3.2 基于整体刚度损伤指标的IDA 分析
与Sa(T1,5%)-Di曲线相同,以整体结构刚度损伤DT作为DM 从结构弹塑性层间位移角达到1/200 时开始记录, 得出各条地震波下结构整体的IDA 曲线,如图5 所示。
由图5 可以看出,在结构整体刚度损伤指标下各条地震动的IDA 曲线均有明显倒塌点,且曲线趋势与层间刚度损伤IDA曲线Sa(T1,5%)-Di类似。 在地震动RSN864 作用下,结构整体也存在明显的“复活”现象,具有趋势一致性。
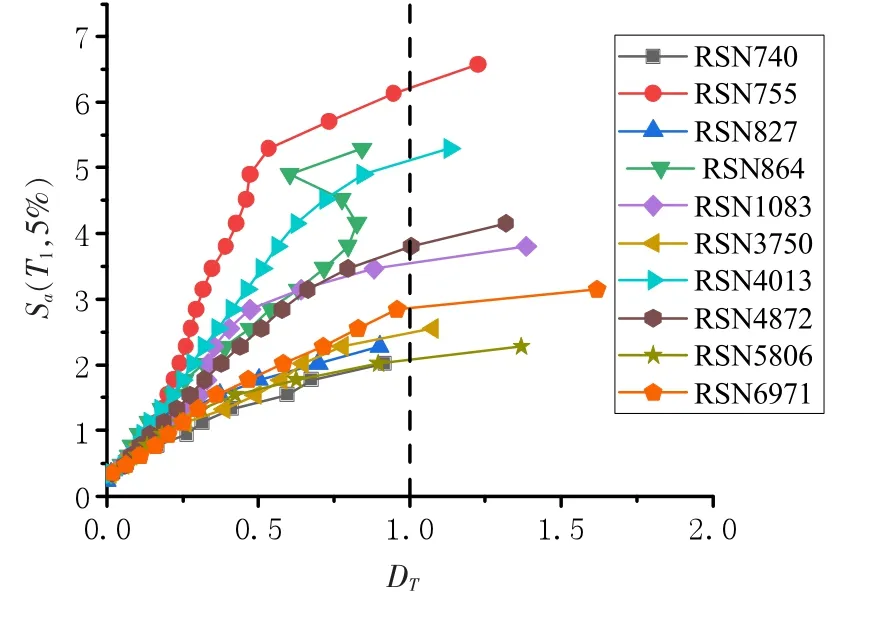
图5 Sa(T1,5%)-DT 曲线图
刚度法认为当结构整体损伤DT到达1 时,结构倒塌。可以从图5 中明显看出,当IDA 曲线斜率到达初始斜率的20%时,多数地震动如RSN755、RSN5806 等作用下的DT没有到达1。从刚度法倒塌判定准则来看,结构未进入倒塌。因此刚度法有低估结构损伤的情况,与文献[11]相符。 以结构整体刚度损伤为DM 的IDA 倒塌判定方法,能处理结构整体刚度损伤DT难以到达1 的困难,有效地解决刚度法的过高估计结构抗震倒塌能力的问题。
4 不同损伤指标下IDA 对比分析
为验证刚度损伤作为DM 的IDA 分析方法的可行性与差异性,与其余不同损伤指标下的IDA 计算分析做评估对比。 以层间位移角θ、残余位移角θr、滞回耗能E 作为DM,可分别得出Sa(T1,5%)-θ、Sa(T1,5%)-θr、Sa(T1,5%)-E 等3 种IDA 曲线。
4.1 Sa(T1,5%)-θ 曲线
层间位移角是最常用的抗震倒塌判定准则,我国规范规定最大弹塑性层间位移角达到1/50 时,结构倒塌。 从图6 看出10 条地震动作用下,1~4 层IDA 曲线接近,斜率均达到倒塌破坏,结构最大层间位移角θmax首先出现在第2 层,其次是第3 层,然后是第1 层。 1~4 层层间位移角均在较小的地震动强度到达规范规定的1/50 倒塌临界点,但IDA 曲线在DM 值为0.02 时的斜率表明结构尚未倒塌。结构倒塌点即IDA 曲线斜率至初始斜率的20%处,均接近层间位移角为0.04,这与美国抗震规范以最大层间位移角为1/25 定义结构倒塌相近[12]。 因此,以最大层间位移角1/50 作为结构倒塌判定标准在一定程度上低估了结构的抗震性能。

图6 Sa(T1,5%)-θ 曲线图
4.2 Sa(T1,5%)-θr 曲线
图7 是以残余层间位移角作为DM 的IDA 曲线簇。结构IDA 初期,即在较低地震动强度下,残余位移差距不大,增大速度缓慢。 在IDA 曲线后期,IDA 分析点离散性较大,在地震动强度加大过程中IDA 曲线斜率大幅度突变,能较为清楚地看出倒塌点。 与上述基于层间构件损伤、层间位移角的IDA 曲线不同,在残余位移角为损伤指标的IDA 分析中,结构顶层的曲线最为突出,而顶部楼层破坏程度应为最小。 图中1~7 层均有倒塌点,且4~7 层的IDA 曲线十分接近,而根据其他损伤指标的IDA 曲线分析看出,结构5~7 层塑性程度较小。 因此该方法不能反映真实结构的整体破坏,无法描绘结构的倒塌模式。
另外,Sa(T1,5%)-θr曲线出现的结构“复活”现象明显增多。 图7(c)、图7(f),图7(i)、图7(j)中曲线随谱加速度增大而斜率逐步变小,符合常理上结构的抗震性能变化。 而在图7(a)、图7(b)、图7(d)中,IDA 曲线均出现了短暂的结构层间应力强化,随后进入倒塌。图7(d)“复活”的现象更是十分突出,折转弧度楼层越低越为明显。
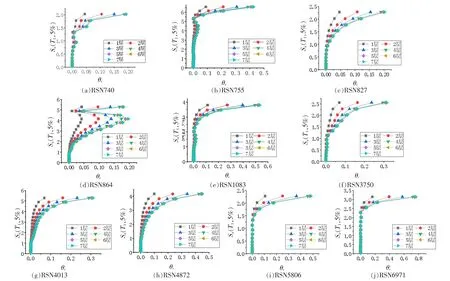
图7 Sa(T1,5%)-θr 曲线图
4.3 Sa(T1,5%)-E曲线
以基底剪力-顶点位移做出力-位移曲线,求出该结构在不同地震动及地震动强度下的滞回耗能E。以结构耗能E 作为DM 得出10 条地震波作用下Sa(T1,5%)-E 曲线。
图8 中,滞回耗能E 随地震动变大,IDA 曲线斜率稳步变缓,没有出现斜率突变、回溯的情况。 该方法在任何地震波下IDA 曲线走向趋势一致,均符合结构的抗震性能反应,但都不能清晰反映出结构细部的损伤破坏变化,也无法体现出结构硬化等状态信息。
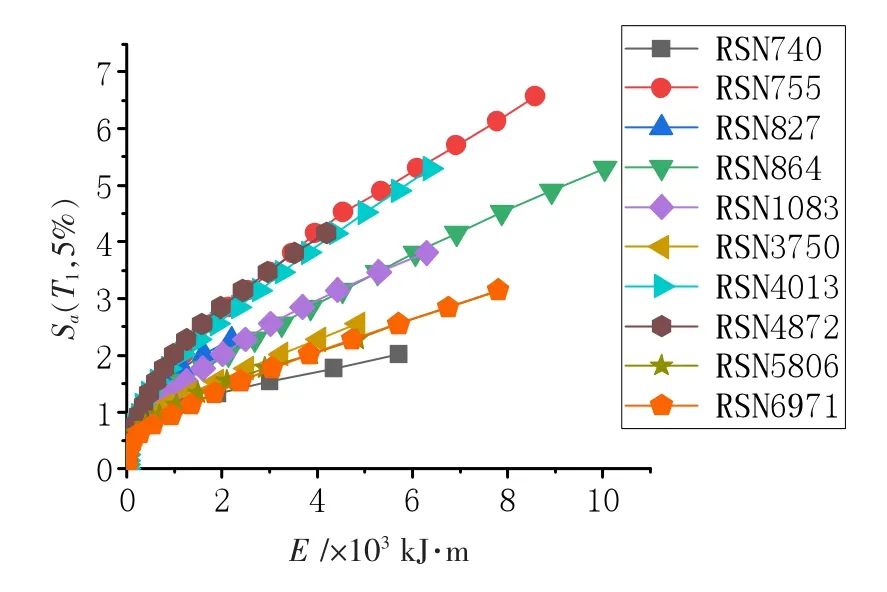
图8 Sa(T1,5%)-E 曲线图
归纳各个损伤指标DM 下的倒塌点所对应的谱加速度于表4 所列。 从表4 中分析得出,DM 为层间构件刚度损伤Di、结构整体刚度损伤DT、层间位移角θ 的IDA 倒塌点相差不大,层间构件刚度损伤与层间位移角的倒塌点基本相同,结构整体损伤的倒塌谱加速度略高于前面两种方法。 其次是基于残余位移角θr的IDA分析,谱加速度倒塌临界点均提前于前三种方法。 最先到达倒塌点的是基于滞回耗能E 为损伤指标的IDA分析倒塌判定方法,每条地震波作用时结构倒塌点都偏小,具有一定的保守性。

表4 不同DM 下倒塌点处对应谱加速度 g
5 结构破坏状态
为了更好地了解模型在不同地震作用下的倒塌情况,验证基于刚度损伤的IDA 方法能较好描述结构倒塌,将最大层间位移角1/25 时的结构状况作为分析阶段,此时各层层间位移角如图9 所示。图9 中最大层间位移角在第2 层,4、5 层的层间位移角相差幅度大,2 层和3 层层间位移角接近。 尤其在地震波RSN6971 作用下2、3 层层间位移角十分接近。
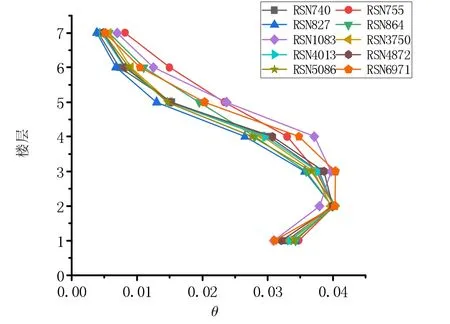
图9 θmax=1/25 时各层层间位移角图
不同地震波导致结构有不同的出铰模式, 图10 为RSN740 作用下的最大层间位移达到1/25 时结构塑性铰程度示意图。 以曲率延性来表述塑性破坏程度,图10 中数值为各构件端部塑性铰的曲率延性,为区别梁柱,柱端曲率延性加以括号表示。 由图10 发现,结构整体呈强柱弱梁状态塑性铰已发展至6 层,顶层还处于弹性状态。 结构破坏程度以中梁大于外梁、梁大于柱为特征。 4 层柱顶出现不同程度的塑性铰导致4 层和5 层损伤值相差较大,两层层间位移角相差较大,观察图4(a)与图6(a)皆可描述这一特点。 1~3 层梁破坏程度接近且最为严重,解释1~3 层Sa(T1,5%)-θ 曲线如此接近的现象,但Sa(T1,5%)-θ 曲线却忽略了底层柱脚的损伤,基于层间构件刚度作为损伤指标的IDA 方法突出显示柱的损伤。 在Sa(T1,5%)-Di曲线中1 层破坏最为严重,2、3 层曲线相近。 该方法能逐个考虑结构梁柱构件的塑性程度,相比其他损伤指标下的IDA 曲线能够更加准确精细地描绘结构的倒塌状态。

图10 RSN740 作用下θmax=1/25 时结构塑性程度图
6 结论
(1)提出的DM 为层间构件刚度损伤Di和结构整体刚度损伤DT的IDA 曲线与层间位移角θ 的IDA 曲线运动轨迹相近,能较好地反映结构损伤破坏情况。 另外,DM 为层间构件刚度损伤的IDA 曲线比起层间位移角作为损伤指标能突出考虑柱损伤的严重性,并且能清晰准确地体现出各层破坏情况;DM 为结构整体刚度损伤的IDA 倒塌判定准则方法能较好地弥补刚度准则的不足。 经过本文计算统计归纳,两者可以作为基于IDA 结构抗震倒塌破坏准则的损伤指标。
(2)DM 为层间构件刚度损伤Di和结构整体刚度损伤DT的IDA 曲线与层间位移角θ 的IDA 曲线倒塌点差距不大,曲线相近。但基于不同损伤指标DM 的IDA 分析中,以残余位移角θr、滞回耗能E 为DM 的IDA曲线,倒塌点普遍提前于前三种损伤指标,过低地估计了结构的抗震强度,具有一定的保守性、冗余度,可以用做重要结构的倒塌评估。

