空间钢构架混凝土梁纯扭性能的有限元模拟分析

张宇阳， 唐兴荣

（苏州科技大学 土木工程学院，江苏 苏州 215011）

空间钢构架是由角钢（弦杆）和缀条（腹杆）焊接而成的一种空间轻钢结构（见图1），将空间钢构架替代传统的钢筋绑扎骨架形成空间钢构架混凝土结构或构件。 轴向荷载下空间钢构架对核心混凝土具有约束作用，可提高混凝土的轴心抗压强度和变形能力[1-5]。 空间钢构架角钢（弦杆）、竖向或斜向缀条（腹杆）以及斜裂缝间混凝土形成空间桁架模型，可提高空间钢构架混凝土构件的截面抗扭承载力。 目前，国内外对空间钢构架混凝土构件的纯扭性能的研究还很少[6-7]，有必要通过试验研究和有限元模拟分析对空间钢构架混凝土纯扭构件的受力性能进行深入的研究。在试验研究的基础上，本文采用ABAQUS 大型有限元软件，以空间钢构架角钢（弦杆）的体积配筋率、缀条（腹杆）的体积配箍率等为设计参数，进行空间钢构架混凝土梁在扭矩作用下的受力性能的模拟分析。 同时，在试验研究和有限元模拟的基础上，基于变角空间桁架理论，建立了空间钢构架混凝土梁受扭承载力计算公式，为实际工程的应用提供技术支撑。

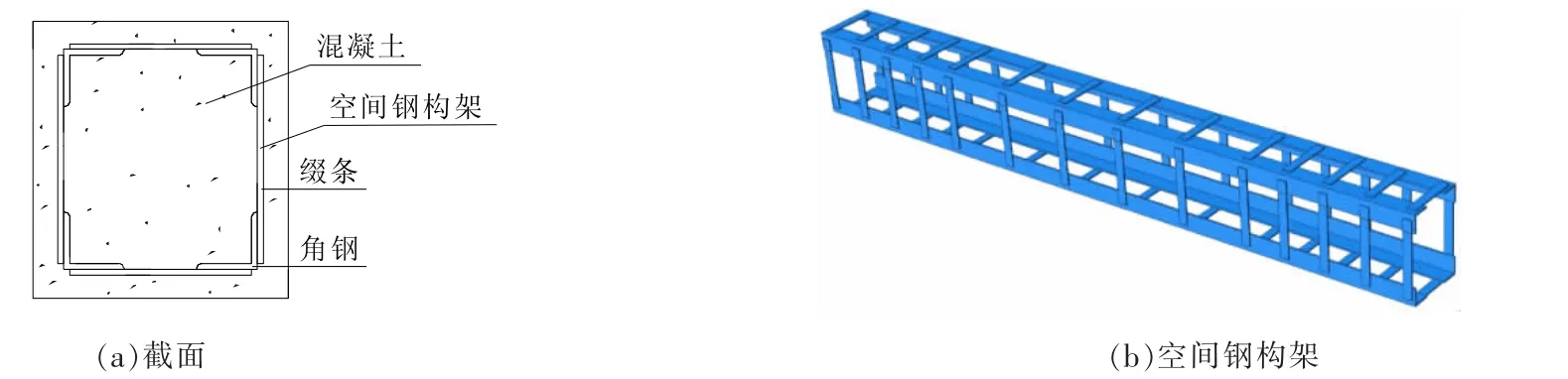
图1 空间钢构架混凝土构件截面

1 试验概况

文献[7]以空间钢构架形式、混凝土保护层厚度、混凝土强度等级等为设计参数，设计制作了6 根空间钢构架混凝土梁和1 根普通钢筋混凝土梁试件。 试件设计参数及主要试验结果见表1 所列。 各试件尺寸均为230 mm×300 mm×2 000 mm，试件配筋见表1 和图2。 角钢（弦杆）（L50×5）实测屈服强度平均值325 MPa，弹性模量2.1×105MPa；缀条（腹杆）（-25×4）实测屈服强度平均值525 MPa，弹性模量2.3×105MPa。

表1 试件设计参数及主要试验结果

图2 试件配筋

加载装置见图3， 试件两端的上下面层铺设沙垫层后分别用反力架夹紧， 试件的固定端在反力架的中部，加载端固定于反力架的左端，反力架右端上部安装伺服作动器，作动器施加竖向荷载给反力架，从而实现试件的纯扭受力。

图3 加载装置

2 有限元模型的建立

采用ABAQUS 大型有限元软件建立了空间钢构架混凝土梁受扭性能的有限元分析模型。空间钢构架的角钢、缀条、混凝土均采用六面体实体单元，即C3D8R 单元。不考虑型钢与混凝土之间的粘结滑移，采用绑定的方式将空间钢构架与混凝土连接到一起。

采用混凝土塑性损伤模型定义混凝土材料， 材料本构选用 《混凝土结构设计规范》（GB50010-2010）[8]（2015 年版）中的本构关系。 受压本构关系

式中，ρc=fc，r/（Ecεc，r）；n=（Ecεc，r）/（Ecεc，r-fc，r）；x=ε/εc，r；αc为混凝土单轴受压应力-应变曲线下降段参数值；fc，r为混凝土的单轴抗压强度代表值；εc，r为与单轴抗压强度代表值fc，r相应的混凝土峰值压应变；dc为混凝土单轴受压损伤演化参数。

受拉本构关系

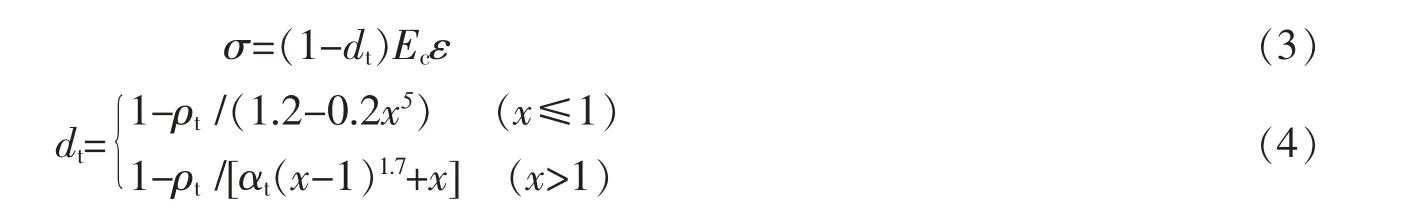
式中，x=ε/εt，r；ρt=ft，r/（Ecεt，r）；αt为混凝土单轴受拉应力-应变曲线下降段的参数值；ft，r为混凝土的单轴抗拉强度代表值；εt，r为单轴抗拉强度代表值ft，r相应的混凝土峰值拉应变；dt为混凝土单轴受拉损伤演化参数。

采用二折线模型定义角钢、缀条的材料属性，屈服前钢材的弹性模量为Es，屈服后取为0.01Es，钢材的泊松比为0.3。

为与试验一致，将加载端的下底面耦合于一个点，并锁定该点处三个方向的位移，即令U1、U2、U3 为0，不限制转角，形成一个球铰。 将固定端的上下两个面的六个自由度锁定，即令U1、U2、U3、UR1、UR2、UR3 都为0，形成固定端。 在加载端的悬臂上施加一个向下的力，通过位移控制，实现扭矩的作用。

在装配模块中，利用移动、阵列、合并等工具将创建好的的部件按照图纸装配成一个整体，如图4 所示。其中，为了与实际的受力方式保持一致，本文按照试验加载装置创建了一个固定端和一个加载端。 梁端的扭矩是通过在加载端悬臂（力臂a=1 000 mm）上施加竖向力实现的，采用竖向力作用线竖向位移控制加载，目标位移200 mm，初始位移为目标位移的1%，采用Newton-Raphson 算法求解非线性问题。

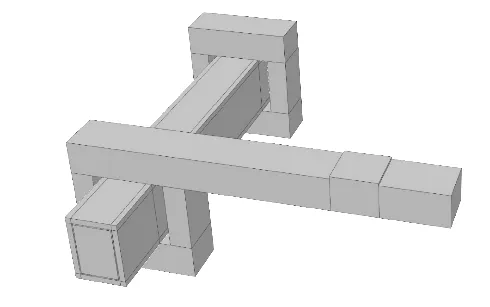
图4 试件装配图

3 有限元模型的验证

采用上述建立的有限元模型对文献[7]的6 根空间钢构架混凝土纯扭试件进行有限元验证分析。 图5 给出了各试件扭矩-扭转角曲线试验值和模拟值的比较，由图5 可见，转矩-扭转角曲线试验值和模拟值吻合较好，整体趋势较为一致，但由于建模时没有考虑型钢与混凝土之间的粘结滑移，前期刚度稍大于试验曲线。极限扭矩的模拟值与试验值比值（Tusimu/Tutest）的平均值为1.022 6，离散系数0.023 4。 这表明按上述方法建立的有限元模型可以用来分析空间钢构架混凝土梁受扭性能。

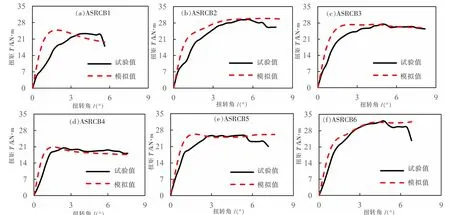
图5 试件扭矩-扭转角曲线试验值与模拟值比较

4 空间钢构架混凝土梁受扭性能模拟分析

为进一步研究空间钢构架混凝土梁的纯扭性能，以空间钢构架角钢（弦杆）的配钢特征值λv,stl、缀条（竖腹杆）的配箍特征值λv,st1等为设计参数，设计了32 个空间钢构架混凝土梁试件及1 根普通钢筋混凝土梁试件（CB0），并1 根设置斜缀条的空间钢构架混凝土梁试件。 试件的截面尺寸均为230 mm×300 mm，试件长度为2 000 mm，混凝土强度等级为C30，角钢（弦杆）采用Q235 钢，缀条（竖腹杆、斜腹杆）采用Q345 钢、Q390钢，混凝土保护层厚度25 mm。 试件设计参数见表2 所列。

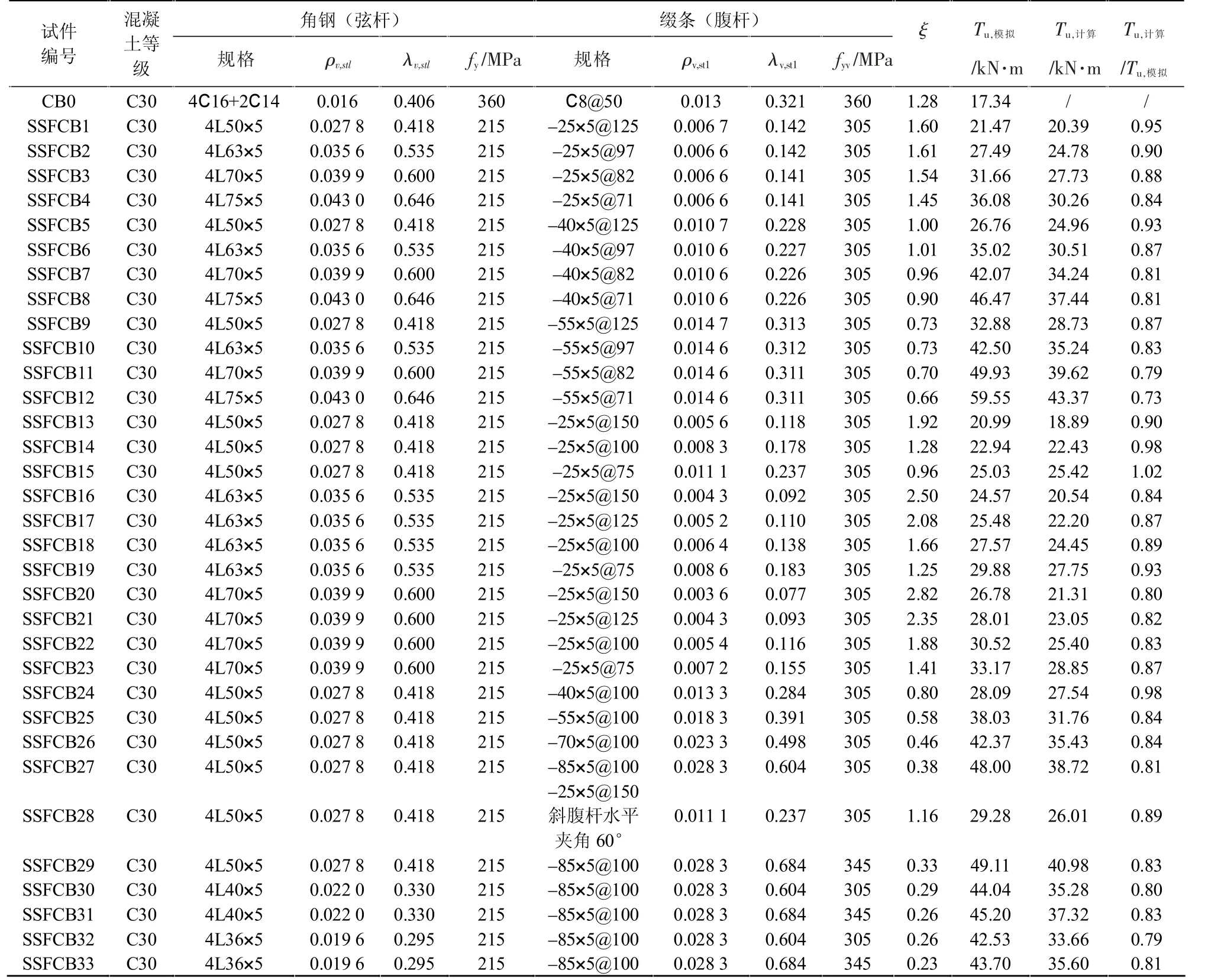
表2 试件设计参数和主要模拟结果

4.1 空间钢构架混凝土梁扭矩-扭转角曲线

加载端梁截面的扭转角最大，在扭矩-扭转角曲线中的扭转角取加载端梁截面扭转角。

（1）缀条（腹杆）体积配箍率不同时。 空间钢构架缀条（腹杆）的配箍特征值

式中，ρv,st1为缀条（腹杆）的体积配箍率，按式（6）计算；fyv为缀条的屈服强度；fc为混凝土轴心抗压强度。Ast1为缀条截面面积；s 为缀条的间距；b、h 分别为截面宽度和高度；lb、ld分别为角钢短边、 长边方向的肢长；ucor为核心截面周长，ucor=2（bc+dc）；bc、dc分别为宽度、高度方向角钢外表面间的距离。

图6 给出了角钢（弦杆）配钢特征值λv,stl=0.418，不同缀条（腹杆）配箍特征值λv,st1时扭矩-扭转角（T-θ）关系。由图6 可见，在λv,stl=0.418 时，随着缀条（腹杆）配箍特征值λv,st1的增大， 极限扭矩和极限扭矩对应的扭转角也随之增大，极限扭矩后，T-θ 曲线较为平缓，具有很好的延性性能。

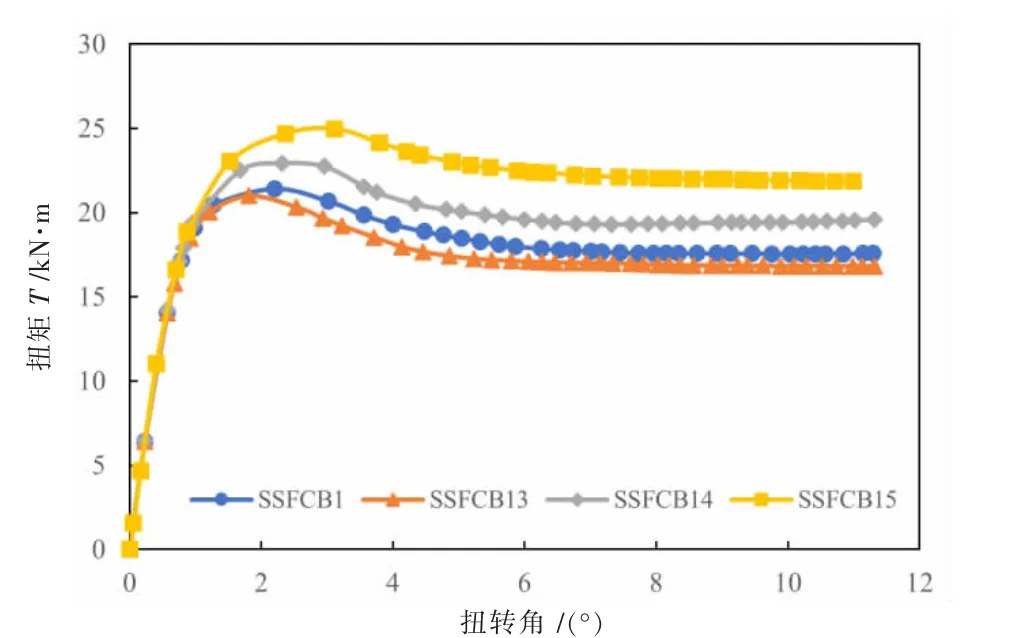
图6 试件截面扭矩-扭转角关系

（2）角钢（弦杆）体积配钢率不同时。 空间钢构架弦杆配钢特征值

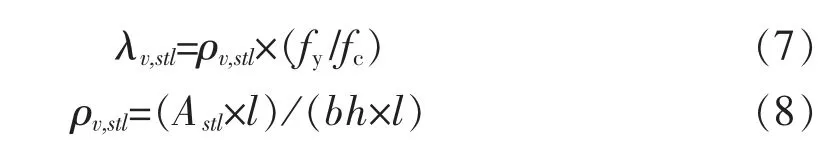
式中，ρv,stl为角钢（弦杆）的体积配钢率，按式（8）计算；fy为角钢（弦杆）的屈服强度；Astl为角钢（弦杆）的总截面面积；fc为混凝土轴心抗压强度。

图7 给出了缀条（腹杆）配箍特征值λv,st1=0.142，不同截面弦杆配钢特征值λv,stl时扭矩-扭转角（T-θ）关系。 图7 中，λv,st1=0.142 时，随着截面弦杆配钢特征值λv,stl的增大，极限扭矩和极限扭矩对应的扭转角也随之增大， 极限扭矩后，T-θ 曲线较为平缓，具有很好的延性性能。

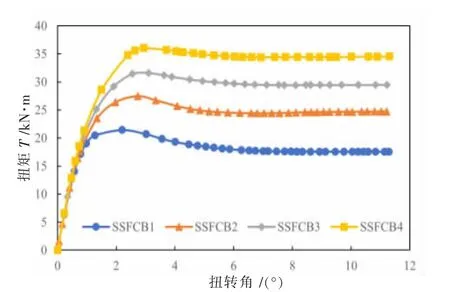
图7 试件截面扭矩-扭转角关系

（3）设置斜腹杆空间钢构架混凝土梁。 试件SSFCB13 为仅有竖腹杆的空间钢构架混凝土梁， 试件SSFCB28 除了设有竖腹杆外，还设置了–25×5＠150 斜腹杆（水平夹角α=60°），其他条件均相同。 图8 给出了试件SSFCB13 和SSFCB28 的T-θ 曲线关系。 由于图8 可见，增加斜腹杆后，试件SSFCB28 的极限扭矩提高了26.55%，极限扭矩时对应的扭转角提高了23.28%，且极限扭矩后T-θ 曲线下降平缓，具有较大的转动能力。 增加斜腹杆可进一步改善空间钢构架混凝土梁抗扭性能。

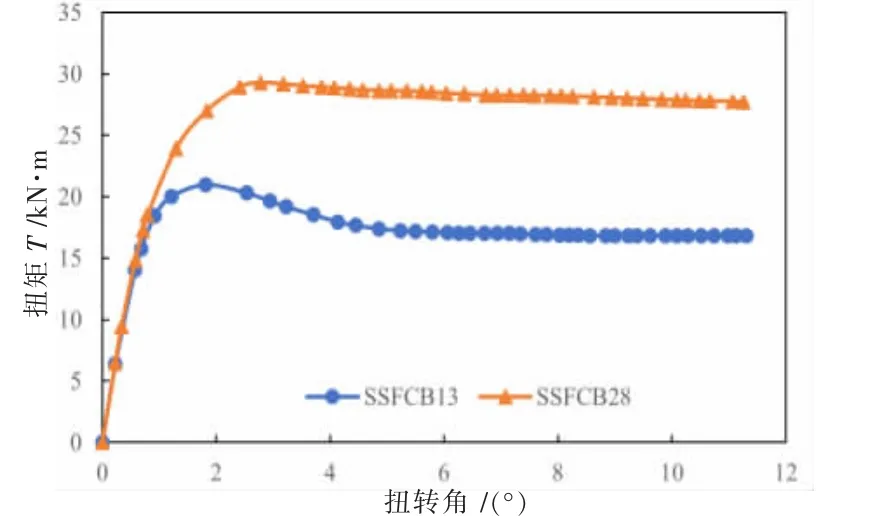
图8 试件截面扭矩-扭转角关系

（4）对比试件。 试件CB0 为普通钢筋混凝土梁试件，SSFCB14 为空间钢构架混凝土梁试件，试件的抗扭角钢（弦杆）和抗扭缀条（腹杆）的配筋强度比ξ 均为1.28。 图9 给出了试件CB0 和试件SSFCB14 的扭矩-扭转角曲线（T-θ），由图9 可见，试件SSFCB14 的极限扭矩及其对应的扭转角分别为试件CB0的1.3216 倍、2.2114 倍，且极限扭矩后，T-θ 曲线比较平缓。 与普通钢筋混凝土梁相比，空间钢构架混凝土梁的抗扭性能有很大的提高。这是由于空间钢构架混凝土梁形成一个带混凝土斜压杆的空间桁架结构来抵抗扭矩的作用，同时，空间钢构架承担部分外扭矩，致使空间钢构架混凝土梁的抗扭性能较普钢筋混凝土梁有较大的提高。

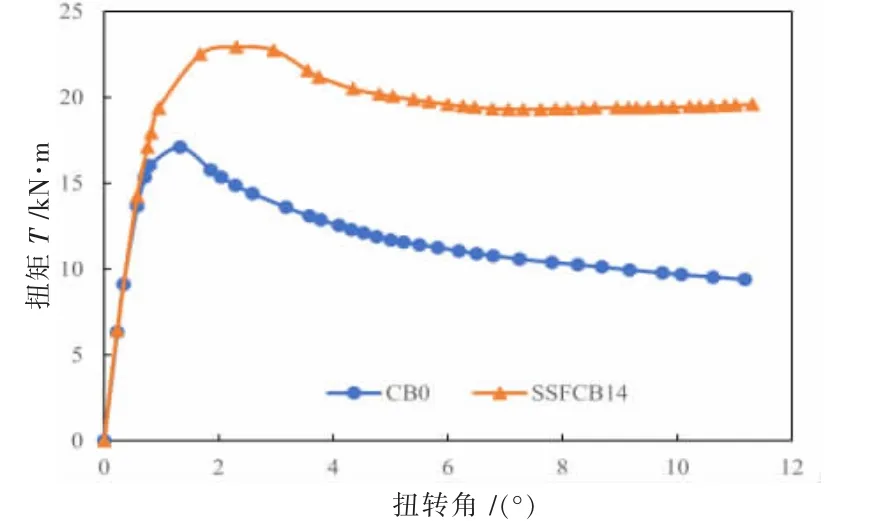
图9 试件截面扭矩-扭转角关系

4.2 空间钢构架混凝土梁抗扭承载力分析

（1）空间钢构架弦杆配钢特征值λv,stl。 图10 给出了在空间钢构架腹杆配箍特征值λv,st1一定时（λv,st1分别为0.1415、0.2268和0.3118）， 极限扭矩与空间钢构架弦杆配钢特征值的关系（Tu-λv,stl）。 由图10 可见，配筋强度比ξ 在0.6～1.7 范围内，空间钢构架腹杆配箍特征值λv,st1一定时，随着空间钢构架弦杆配筋特征值λv,stl的增大，试件的极限扭矩逐渐增大，且λv,st1越大，试件的极限扭矩也越大。

图10 Tu-λv,stl 曲线

（2）空间钢构架腹杆配箍特征值λv,st1。 图11 给出了在空间钢构架角钢 （弦杆） 配钢的特征值λv,stl一定时 （λv,stl分别为0.418、0.535 和0.600），极限扭矩与空间钢构架缀条（腹杆）配箍特征值的关系（Tu-λv,st1）。 由图11 可见，配筋强度比ξ 在0.9～2.7 范围内，空间钢构架角钢（弦杆）配钢特征值λv,stl一定时，随着空间钢构架缀条（腹杆）配箍特征值λv,st1的增大，试件的极限扭矩逐渐增大，且λv,stl越大，试件的极限扭矩也越大。

图11 极限扭矩与腹杆配箍特征值曲线Tu-λv,st1

（3）抗扭弦杆与抗扭腹杆配筋强度比ξ。 考虑斜腹杆抗扭作用时，抗扭弦杆与抗扭腹杆配筋强度比

图12 给出了试件极限扭矩与配筋强度比的关系（Tu-ξ），由图12 可见，空间钢构架混凝土梁极限扭矩Tu随配筋强度比ξ 的减小而较为明显地增大。 当ξ＞2.0 时，抗扭角钢（弦杆）配置较多，极限状态时抗扭角钢（弦杆）不屈服，抗扭缀条（腹杆）屈服，极限扭矩变化不大；当ξ＜0.5 时，抗扭缀条（腹杆）配置较多，极限状态时抗扭角钢（弦杆）屈服，而抗扭缀条（腹杆）不屈服，抗扭承载力提高不大。

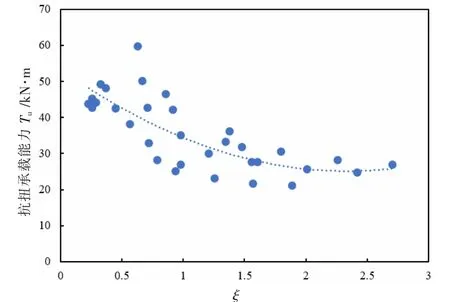
图12 试件极限扭矩与配筋强度比的关系（Tu-ξ）

5 空间钢构架混凝土梁受扭承载力计算

空间钢构架混凝土梁纯扭构件的破坏形态与普通钢筋混凝土梁纯扭构件类似[7]。 因此，本文提出将空间钢构架混凝土梁的角钢（弦杆）和缀条（腹杆）按截面面积不变，形心位置不变分别等效为钢筋混凝土梁中的纵筋和箍筋，采用空间变角桁架模型理论计算空间钢构架混凝土梁的极限扭矩。 计算基本假定：（1）斜裂缝间的混凝土只承受压力，具有螺旋形的空间裂缝的混凝土外壳组成桁架的斜压腹杆；（2）角钢和缀条只承受拉力，分别为桁架的受拉弦杆和受拉腹杆；（3）不考虑核心区混凝土及角钢的销栓力的抗扭作用。

为了与《混凝土结构设计规范》（GB50010-2010）（2015 年版）[8]的纯扭极限承载力计算公式相一致，提出空间钢构架混凝土梁纯扭极限承载力计算公式

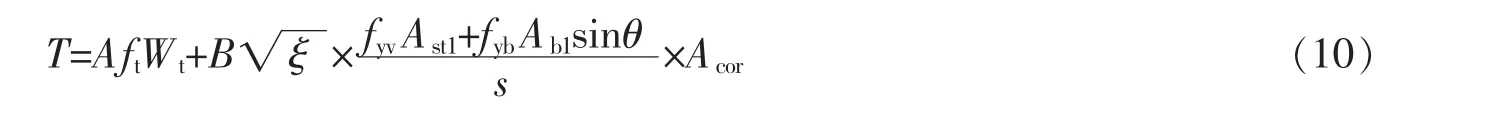
式中，A、B 分别为混凝土受扭作用系数和空间钢构架受扭作用系数，由试验或有限元模拟确定；fyv为缀条（腹杆）的屈服强度；Ast1为单肢缀条截面面积；Acor为截面核心部分的面积； ξ 这考虑斜腹杆抗扭作用时，抗扭弦杆与抗扭腹杆配筋强度比，按式（9）计算，建议0.5≤ξ≤2.0；其余符号同前。

根据32 个模拟试件和文献[7]6 个试验试件数据，经回归可得A=0.37，B=1.10（见图13），即

图13 式（11）与试验值、模拟值比较

由式（11）得到的极限扭矩与模拟值和试验值吻合较好，公式计算值与有限元模拟值和试验实测值的平均比值为0.979 0，离散系数为0.133 5，相关系数0.876 6，公式的计算值与模拟值和试验值吻合较好，可以用来计算空间钢构架混凝土梁纯扭极限承载力。

6 结论

（1）模拟得到的各试件的扭矩-扭转角曲线与试验得到的相应曲线吻合较好，极限扭矩相差不超过10%，认为该模型可行，可以用来模拟空间钢构架混凝土梁的纯扭性能。

（2）空间钢构架混凝土梁较普通钢筋混凝土梁有更好的纯扭性能，其极限扭矩与空间钢构架抗扭弦杆配钢特征值λv,stl、空间钢构架抗扭腹杆配箍特征值λv,st1成正比，且当λv,stl提高，λv,st1对空间钢构架混凝土梁极限扭矩的影响提高；当λv,st1提高，λv,stl对空间钢构架混凝土梁极限扭矩的影响也提高。 另外，斜缀条的设置也可大幅度提高空间钢构架混凝土梁的纯扭性能。

（3）空间钢构架混凝土梁的极限扭矩Tu随抗扭弦杆和抗扭腹杆的配筋强度比ξ 的减小而较为明显地增大，当ξ＜0.5 或ξ＞2.0 时，Tu变化不大，因此，建议空间钢构架混凝土梁的配筋强度比取值范围0.5～2.0。

（4）空间钢构架混凝土梁极限扭矩的计算公式的计算结果与模拟数据和试验数据吻合较好。