基于扩展Petri网的复杂装配线建模*

何 磊，李 涛，张世炯，唐健钧

（航空工业成都飞机工业（集团）有限责任公司，成都 610091）

先进航空航天制造业的技术水平不仅体现在具体产品的设计和制造能力上，同时还体现在对产品生产线的设计、评估和改进上。由于现代大型飞机等复杂产品一般由大量不同特性的零件、设备组成，涉及多种装配和试验工艺，生产线效能受到产品生产流程、生产线布局、人力资源配置、设备效能、设备故障率、物流及供应链系统效能等多方面因素影响，单一算法已经很难对飞机这样的复杂产品生产线做出有效评估。在这样的背景下，出现了许多生产线建模理论和相应仿真技术，其中以Petri 网建模理论和离散事件建模理论应用最为广泛。

Petri 网因其数学定义严谨简洁，同时能进行图形化建模，建模结果直观明了，能够表达生产过程中的顺序、冲突、并行和同步等过程。借助数学工具，能够快速对Petri 网进行静态的结构分析和动态的行为分析。

使用离散事件建模软件进行仿真具有结果直观、易于分析的特点，但是建模结果与实际场景密切相关，建模规律难以总结，模型质量与使用者专业水平密切相关，同时仿真元素增加后各种规则设置较为复杂，修改维护不便。

Petri 建模和离散事件建模均有其优缺点，将二者结合使用能够充分发挥二者的长处，取得更好的仿真效果。

本文综合利用扩展Petri 网建模和离散事件建模理论，为复杂装配系统建模仿真提供了进一步的思路。

Petri 网及复杂装配系统建模研究现状

1 基础Petri网模型

Petri 网是一个三元组，记为N=(P，T；F)，P代表库所(Place)，T代表变迁(Transition)，F代表网系统的流关系(Flow relation)。

其中F⊆(P×T)∪(T×P)，F是从变迁到库所和从库所到变迁所构成二元组的集合。

绘制Petri 网时，一般用圆形表示库所，用矩形表示变迁，用有向弧表示库所到变迁、变迁到库所之间的连接关系。Token 用实心圆点表示，Petri 网初始时Token 放置在库所中，当变迁不断激发后，Token 便在库所和变迁间流动。

2 Petri网及复杂装配系统建模研究

利用赋时着色Petri 网能够对柔性制造单元和柔性制造系统（FMS）进行建模[1]和多目标仿真优化[2]。在飞机装配领域，已进行了大量利用扩展Petri 网进行生产线建模的研究工作[3-6]，通过扩展Petri 网可以表达飞机装配工艺流程及不同工序间的依赖关系，通过启发式算法可以对所构建模型进行优化求解。

但上述研究工作主要侧重于装配工艺流程的建模与仿真，对于装配生产线中的资源限制和配置情况考虑较少，优化结果与实际生产有一定差距。徐开元等[7]利用多域集成Petri 网构建了飞机装配系统模型，系统地构建了装配资源系统各领域的形式化表达模型，但仅停留在定性研究。

利用Petri 网建模的缺点在于数据量上升后容易引发状态空间爆炸问题。引入时延、着色、面向对象、随机等特征后，Petri 网的表达能力得到了增强，但同时也丧失了一定数学表达和分析能力。在这种情况下，离散事件建模理论及相应仿真软件体现出优势。离散事件建模软件如Witness 等提供了丰富的模型单元，能够进行交互式建模，同时提供了运行仿真、数据交互、统计展示、模型优化等功能。

浙江理工大学洪渊泉[8]利用Witness 软件建立了某叉车厂的内燃车总装线仿真模型，并利用改进粒子群算法对模型进行最优求解，得到叉车混流装配线的最优投产顺序。上海交通大学杨枨[9]对无锡博世公司喷油嘴配件生产线进行分析，针对零件的生产模型进行建模，重点针对制造过程随机情况下的分组装配方法中零件尺寸的设计问题，提出将其作为系统的优化参数之一，通过仿真求解其最优设置。上述研究工作主要面向小型产品装配及零件生产，并不能很好地支持复杂产品装配生产线模型的构建。合肥工业大学王婷[10]以航天产品装配过程平衡为研究对象，通过合理地划分装配单元，对复杂的物流过程进行建模与仿真优化，建立了以平滑指数最小为目标，以给定装配工艺内容、车间布局、物流路径为约束条件的优化模型，并通过改进的遗传算法进行关键设备数量的求解，取得了较好效果。航空工业成都飞机工业(集团)有限责任公司的李涛等[11]针对飞机总装生产线的仿真建模方法进行了初步研究。温乐等[12]利用Petri 网及Witness 仿真软件对转向架生产装配系统进行了建模及仿真优化，但模型规模较小，仅针对简单产品的装配场景。

综上所述，目前在复杂装配系统建模领域，现有研究内容主要侧重于针对具体场景，对于如何将复杂装配系统生产运行逻辑转换为可进行分析仿真的模型，仍然缺乏一套行之有效的指导理论和方法。针对上述问题，本文进一步地将扩展Petri 网引入复杂装配系统建模中，总结复杂装配系统特点，利用扩展Petri 网在数学上对装配单元模型以及复杂装配系统分层模型进行构建和表达，并给出从扩展Petri 网模型到离散事件仿真模型的映射转换关系，从而提出一套有数学支撑、可复用和扩展、通用的复杂装配系统建模理论和方法。

复杂装配系统建模方法

1 定义

装配系统的核心要素是产品、工艺流程和资源，核心要素外又有物流系统和信息系统。产品决定了装配系统的复杂程度和生产环境、生产工艺、质量控制要求等基础属性。工艺流程决定了装配系统的具体形态，目前装配系统的形态主要有3 种，分别为固定式、脉动式和流水线式。

装配系统中涉及到的资源主要可分为两类，即消耗性资源和循环使用资源。消耗性资源指随着产品生产过程不断被消耗的资源，如水、电、气、液及各种物料等。循环使用资源指在产品生产过程中能够被循环申请使用和释放的资源，包括设备、工装、人员等。

2 特点

对于一类复杂产品装配生产线，如航空器、航天器装配生产线等，每一个装配单元进行小部分工作，同一时间可能有多个装配单元工作，这意味着产品无法在装配单元中流动，因为在同一时间模型中存在多个装配单元请求同一产品，这在装配生产线仿真模型构建时是无法实现的。由于装配生产线仿真模型中的装配单元网络通常很大，装配单元的数量可能达到几百上千个，而不同装配单元可能涉及同样的物理空间位置，无法按照装配单元的实际物理位置进行建模，因此无法使用传统装配生产线仿真建模手段实现这类复杂产品的装配生产线仿真模型构建。

3 循环使用资源模型

在流水线式生产中，设备、工装及人员等会按照产品生产工序要求固定到相应工位，因此不存在资源的循环申请和释放过程，从而降低了产品生产周期。

对于固定式、脉动式生产，受生产成本、场地限制，无法将所有设备、工装及人员全部配置到固定工位，必须按照产品生产工序进行资源的循环申请和释放，额外增加了调度和等待时间，因此循环使用资源的方式会影响产品的生产周期。

构建循环使用资源模型时，通常会将设备、工装及人员等实体资源考虑在内。但对于复杂产品装配生产线，如航空器、航天器装配生产线等，操作空间也是重要限制因素。从工艺流程、设备、工装及人员需求考虑，某些工序可能同时具备执行条件，但由于产品中能够容纳开展工作的空间有限，这些工序无法同时开展。如果不将操作空间作为一种资源加以建模和考虑，仿真结果将会引入额外误差。有必要根据产品结构构建操作空间资源模型，将操作空间视为一种可以循环申请和释放的资源加以考虑。

如图1所示，航空器中通常根据功能需求将产品划分为若干个舱位，每个舱位中安装若干部件，根据舱位大小，舱位能够容纳若干人员同时开展工作，每一个舱位可以视为一个操作空间，操作空间的大小定义为其能够容纳同时开展工作的人员数量。

图1 典型的飞机舱位操作空间限制Fig.1 Typical example of operations constraints in a limited aircraft bay

4 分层模型

如图2所示，装配生产线仿真模型由物理仿真层和逻辑仿真层组成。在产品装配过程中，循环使用资源可以被周期性申请和释放。消耗性资源可以在产品装配过程中被申请和消耗。

图2 复杂产品装配线的物理层和逻辑层模型Fig.2 Physical-layer and logical-layer models of a complex product assembly line

物理仿真层用于表达产品在真实空间中的物理位置、装配过程中发生的移动以及产品本身的变化。物理仿真层由若干个装配站位、循环使用资源、消耗性资源构成。站位表示产品装配过程中的某个阶段，在该阶段，产品的物理位置相对固定，在该位置完成一些装配、测试、调试或检验工作。产品的装配过程可以划分为若干个站位，上一个站位的工作结束后，产品移动到下一个站位。站位内的工作可以划分为若干个工序，所有工序完成后表明该站位工作结束，产品可移动到下一站位。产品在站位间依次移动，没有跨越站位的情况。

逻辑仿真层用于表达每个站位中各工序间依赖关系、工序执行顺序、工序对循环使用资源的申请和释放、工序对消耗性资源的申请，工序开始执行、等待、执行完毕的状态判定。在逻辑仿真层中将物理仿真层里的站位映射为一系列具有一定相互依赖关系的工序的集合。

基于扩展Petri 网的模型

1 扩展Petri网模型

利用简单Petri 网能够表达静态结构和网络运行时的动态特性。但是简单Petri 网中没有时间概念，只要前集库所中的Token 数量满足条件就会即时激发。对于实际物理系统而言，时间是非常重要的，在Petri网中加入时间延迟可以为实际物理系统的分析带来方便，将时间延迟与变迁关联，可得到赋时变迁Petri 网（Timed transition Petri net,TTPN）。

赋时变迁Petri 网的运行规则如下：当变迁激发时，该变迁的所有前集中的库所移去输入有向弧上权值所对应的Token 数量，然后变迁等待一定时间再激发，激发后按照输出有向弧上权值所对应的Token 数量输出至后集中的库所。

Petri 网的一个重要特性是冲突（Conflict），即在某个标识状态M下，Petri 网中存在两个或多个变迁同时处于可激发状态，但是由于它们的一些输入库共享，此时一个变迁的激发将导致其他的变迁无法激发。Petri网的冲突特性是实际物理系统中对于资源竞争的体现。

简单Petri 网中并没有给出发生冲突时的解决方式，一种解决方法是随机选定变迁进行激发。但是这种方法引入了不确定性，难以分析冲突对Petri 网运行性能所造成的影响。特别是对于航空器、航天器装配生产线，操作空间是一种竞争激烈的资源，因此Petri 网中将会产生大量的冲突。如果采用随机选定的方法，由于执行结果的不确定性，将会对性能分析和优化造成很大的困难。

为了解决上述问题，可定义如下具有优先级的赋时变迁Petri 网（Priority timed transition Petri net,PTTPN），为一个8 元组：

PTTPN={P,T;F,K,W,M,R,D}

其中,Σ=(P,T;F,K,W,M)为一个库所变迁系统，定义与之前相同。

R={r1,r2,…,rm}为所有变迁的执行优先级集合，其中ri是ti的执行优先级。当多个变迁同时具备激发条件时，执行优先级高的先激发。

D={d1,d2,…,dm}为所有变迁的时延集合，其中di是ti的时延。

2 基于PTTPN的装配生产线单元模型

如图3所示，利用具有优先级的赋时变迁Petri 网可以构建装配生产线单元模型，每一个单元模型代表装配生产线中的一道工序。单元模型Petri 网中的库所、变迁及含义如表1所示。表中，当变迁T0 满足激发条件时，会首先从前置工序所对应库所P0、P1、P2 中取出Token，并从循环使用资源P5、消耗性资源P6 取出相应数量Token，延迟一定时间后，将Token 输出至后置工序所对应库所P3、P4，向循环使用资源库所P5释放Token。上述单元模型Petri 网能够基本满足装配生产线建模需要，但是对于某些工序仍不能满足要求。如对于某些装配工序，并非在工序开始时就申请所有的资源，而是分阶段进行申请，如按照工作的推进，陆续在不同的操作空间开展工作，或人员、设备需求等发生变化。如果在工序开始就申请所有的资源，将会造成资源的大量闲置、等待和浪费，同时可能会造成模型的死锁，并引入额外的建模误差。在此情况下，可以按照图4所示多循环单元模型Petri 网进行建模。

图3 单元模型Petri网Fig.3 A unit model in Petri net

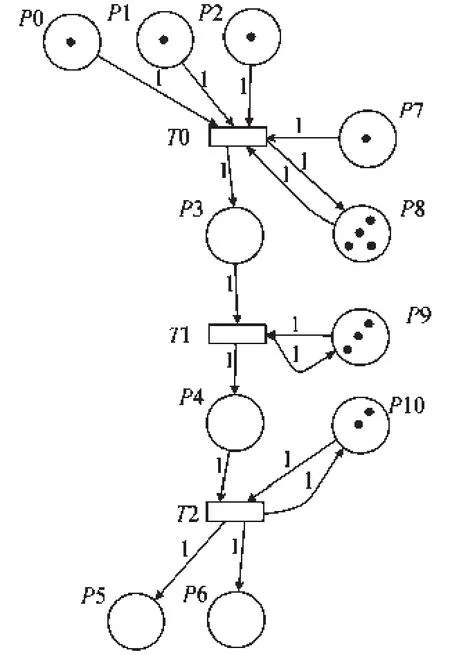
图4 多循环单元模型Petri网Fig.4 Multi-cycle units model in Petri net

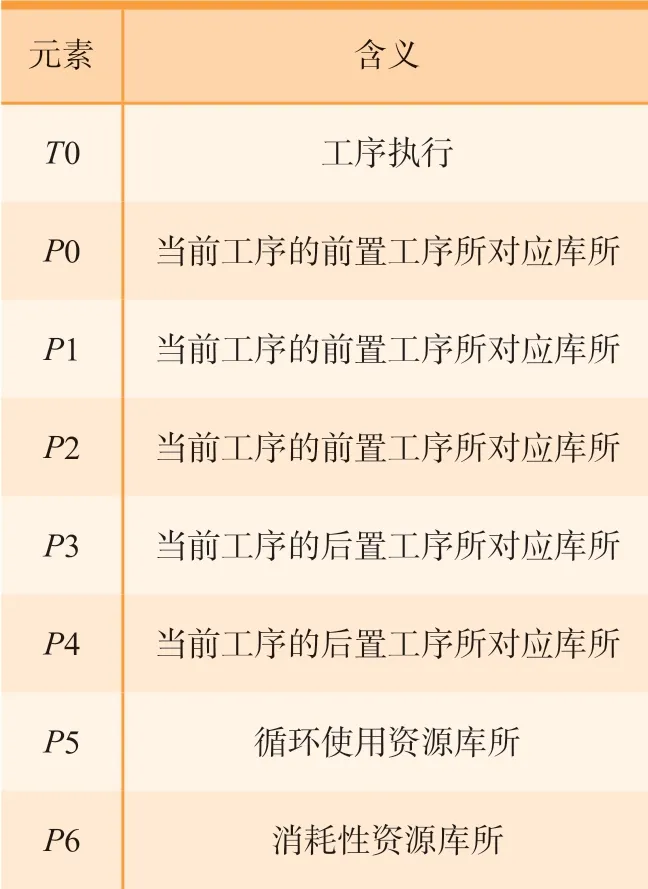
表1 单元模型Petri网中库所、变迁及含义Table 1 Place,transition and definition of a unit model in Petri net

多循环单元模型Petri 网中的库所、变迁及含义如表2所示。

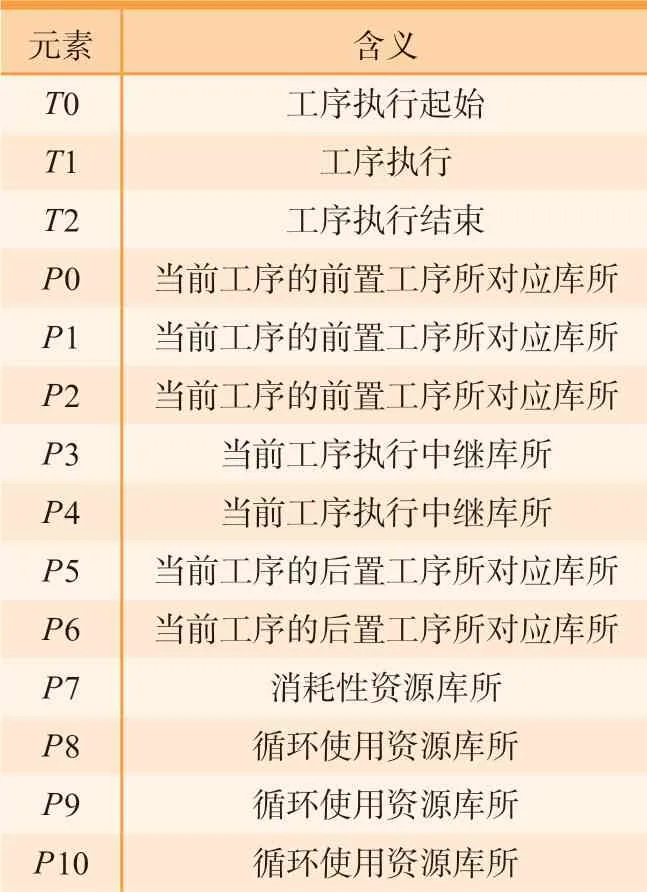
表2 多循环单元模型Petri网中库所、变迁及含义Table 2 Place,transition and definition of multi-cycle units in Petri net

变迁T0、T1 和T2 为同一个工序的不同工作阶段，当变迁T0 满足激发条件时，会首先从前置工序所对应库所P0、P1、P2 中取出Token，并从循环使用资源库所P8、消耗性资源库所P7 取出相应数量Token，延迟一定工作时间后，释放循环使用资源，并将Token 输出至中继库所P3，变迁T0、T1 和T2 的和为该工序的总工作时间，根据实际情况，变迁的数量可能会变化。

复杂装配系统建模实例

1 装配生产线建模仿真输入条件及约束

装配生产线建模仿真所需输入条件可从人、机、料、法、环5 个方面进行，其中人员、工装设备和空间舱位可按照循环使用资源进行建模，物料成品可按照消耗性资源进行建模,如表3所示。

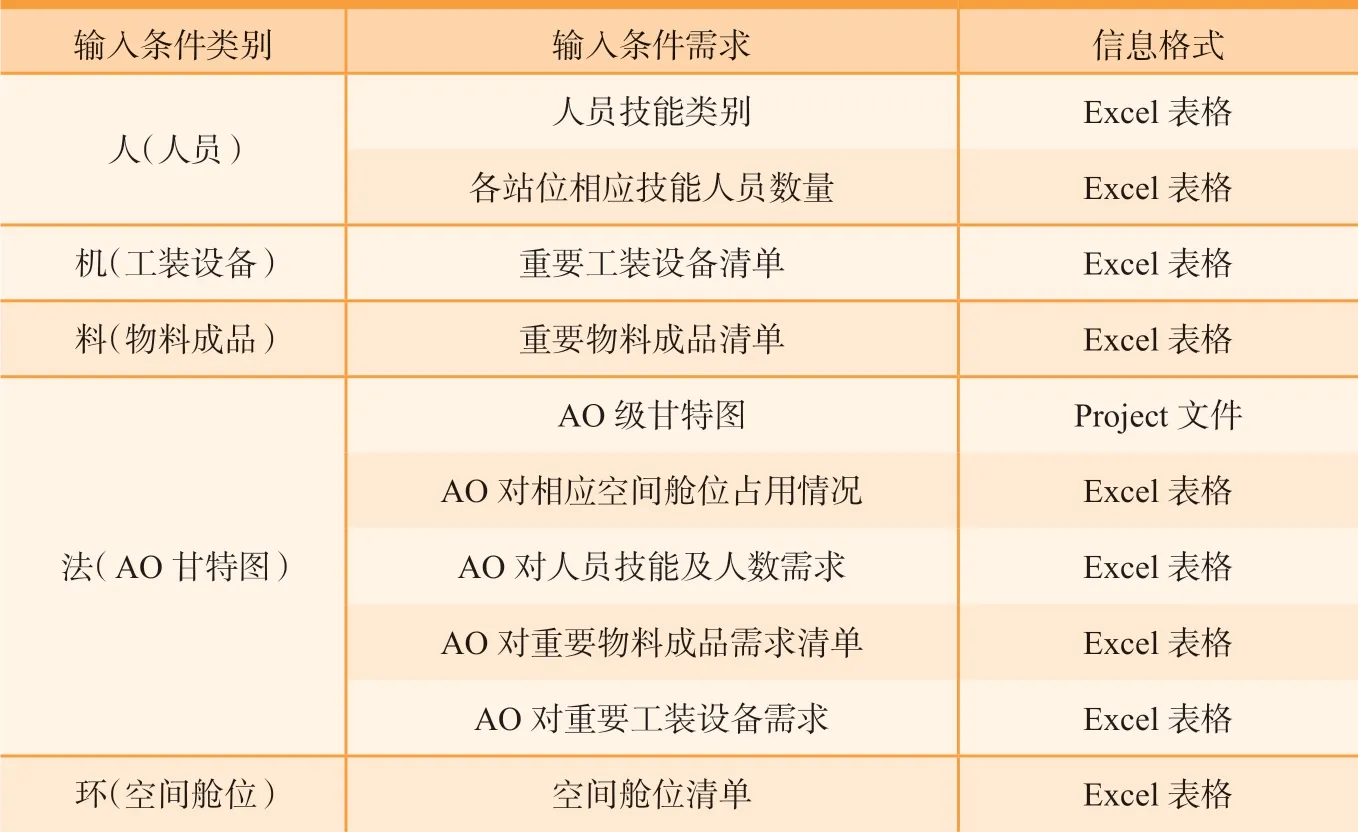
表3 建模输入条件Table 3 Modelling input information

在进行复杂装配生产线建模仿真时还有几个约束条件需要注意，上述输入条件中所列的均为刚性约束，在实际生产过程中还存在许多扰动因素，如产品故障、物料缺件等。在复杂装配生产线中，这类扰动通常难以进行准确的统计和建模，一种可行的建模方法是将这些扰动折算到生产线单元模型的工作时间中，具体建模和折算方法不在本文讨论范围中，以下建模过程约定不考虑产品故障、物料缺件带来的影响。

2 装配生产线仿真模型构建

根据PTTPN 可在离散事件仿真软件中构建装配生产线单元模型，以下以Witness 为例说明构建过程。

离散事件仿真软件中通常提供了多种建模基础元素，可以建立这些元素与PTTPN 中定义的映射关系，如表4所示。

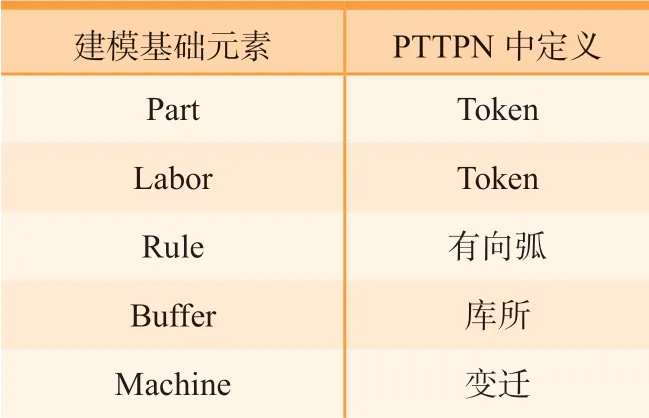
表4 建模基础元素Table 4 Basic modelling elements

在Witness 中构建装配生产线单元模型的逻辑如图5所示。

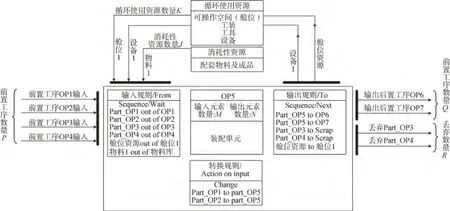
图5 装配生产线单元模型Fig.5 Assembly line unit model

装配单元模型主要由4 部分构成，包括装配单元自身、输入规则、输出规则及转换规则，通过图6 中的3种规则，装配单元能够与生产线仿真模型中的其他装配单元形成依赖网络，并对生产资源进行请求和释放，装配单元模型能够很好地体现实际生产中生产线装配运行逻辑。

在Witness 中构建的单元模型如图6所示，为防止Part 元素进入错误的缓冲区，在Machine 与Buffer间添加Convey 元素，当Machine 输出一个Part 后，即将Convey 设置为Broken，直到新的Part 进入Machine后再将Convey 设置为Repair。对于多循环单元模型Petri 网，可将Machine 设置为多循环类型，每一个循环代表一次变迁。

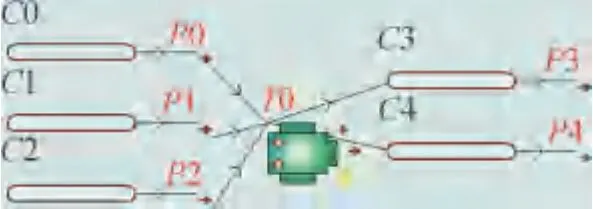
图6 Witness工具中的单元模型建模Fig.6 Modelling of unit by Witness

根据工艺流程，连接多个单元模型，可以得到装配生产线站位模型，如图7所示。可以看出，站位模型由多个单元模型组合得到，一个单元模型可以多个输入和输出，同时单元模型还可以对空间舱位资源进行申请和释放，利用上述方式可以组合得到复杂装配系统模型。

图7 装配生产线站位详细建模Fig.7 Detailed modelling of assembly line workstation

3 仿真模型性能分析

通过构建得到的装配生产线站位模型，可以对生产线进行性能分析，并可通过试验分析不同资源配置对于生产节拍的影响，寻找最优资源配置。如图8所示，站位人员配置变化对站位节拍有明显影响，但随着人数增长，边际效应开始出现，站位节拍趋于稳定，从图8 中可以看出，推荐的人员配置为20 人，此时站位节拍为1723min，即3.6 个工作日。

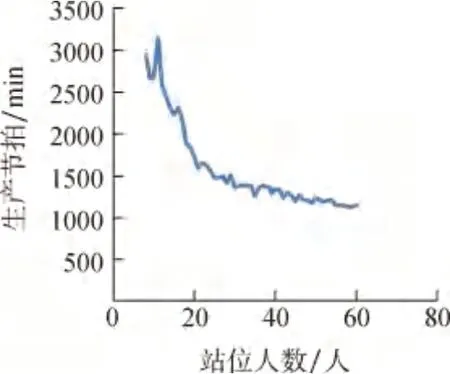
图8 站位生产人数与节拍的关系Fig.8 Relationship between count of workers and workstation cycle-time

如图9所示，通过生产线仿真模型还可对站位人员利用率进行分析，可以看出，人员利用率最高的时段为前两个工作日，之后的人员利用率均低于60%，因此可以对人员作灵活配置，将部分人员分散到其他站位工作。

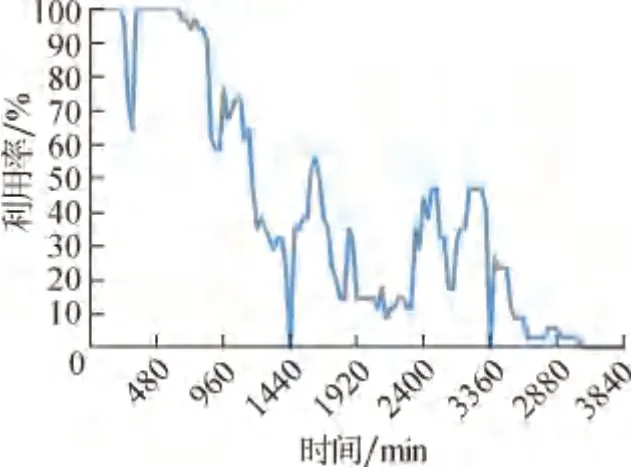
图9 站位人员利用率Fig.9 Utilization of human resources in a work station

结论

本文所提出的复杂装配系统分层模型，能够解决复杂装配系统建模中物理空间位置与装配工艺流程间的矛盾，体现复杂装配系统中工序级的依赖关系和运行资源需求，在多种资源约束条件下给出工序执行序列，同时能够评估复杂装配系统在给定资源配置和工艺流程条件下的节拍、产能及运行效率，通过仿真试验对复杂装配系统提出优化建议。

基于PTTPN 和分层模型的复杂装配系统建模方法能够很好地体现复杂产品装配生产线运行逻辑，并提供了一个基础模型优化平台，但在离散事件仿真软件中进行模型构建仍较为繁琐，维护修改不便。未来可针对离散事件仿真软件进行自动化建模研究，同时可进行各种算法研究，用以对工艺流程及生产线配置进行优化，如可通过优化不同工序执行优先级来缩短生产节拍，提升装配生产线产能。