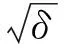反向Ⅱ型fold-fold的正则化系统的动力学分析
方之昊, 陈兴武
(四川大学数学学院, 成都 610064 )
1 引 言
平面逐段光滑系统被广泛地应用于建筑、机械、电网等领域[1-5],它的研究是微分动力系统研究热点之一.本文利用S-T正则化方法来构造反向II型fold-fold逐段光滑系统的正则系统. 这类逐段光滑系统有一个焦点, 且在一定条件下会在参数扰动时产生一个极限环, 类似于解析系统中的Hopf分岔. 本文给出了正则系统在双参数扰动下的局部动力学行为, 指出正则系统的平衡点要么为结点, 要么为焦点,且焦点的稳定性和阶数会随着参数变化而变化.这就导致Hopf分岔的发生.
考虑一个有如下形式的平面系统
(1)

X±(x,y)=(P±(x,y),Q±(x,y))T
为定义在R2上的光滑向量场. 我们称系统(1)为一个逐段光滑系统,y=0为切换流形Σ,并且系统
(2)
为上子系统, 系统
(3)
为下子系统.
Filippov[6]针对此类系统做出了大量的研究和总结, 其成果被后人称为Filippov约定.对于切换流形Σ上任意一点p:(x,0), 定义



(4)

如果H(x)=0, 则p要么是某子系统的平衡点, 要么是某个子系统的切点. 若是前者, 我们称p是逐段光滑系统(2)的边界平衡点; 若是后者, 我们称p为逐段光滑系统(1)的切点. 不失一般性,p固定为原点(0,0). 假设(0,0)是一个切点.若
则称切点(0,0)是逐段光滑系统(1)的一个fold-fold. 若进一步有
P+(0,0)>0,P-(0,0)<0,
则称切点(0,0)是逐段光滑系统(1)的一个反向II(Invisible-Invisible) 型fold-fold. 如图1所示.

图1 蓝色(橘色)虚线表示上(下)子系统轨道(线上彩色)Fig.1 The blue (orange) dot curve denotes the orbit of upper(lower) subsystem(color online)
在本文中, 我们假设(0,0)是逐段光滑系统(1)的反向II型fold-fold. 由文献[7]提出的正则化理论, 逐段光滑系统(1)有如下形式的正则系统
(5)
其中0<ε≪1,


文献[8]发现了正则系统的快慢结构, 文献[9]发现了快慢系统的临界流形和慢子系统向量场分别与滑行区域和滑行向量场是微分同胚的. 随后,文献[10]研究了Saddle-fold类型的正则系统并给出分岔图.文献[11]在某非退化条件下给出了反向II型fold-fold正则系统的焦点量对正则函数φ(s)的依赖关系并进一步给出Hopf 分岔曲线.文献[12]研究了反向II型fold-fold为0.5阶细焦点时正则系统的动力学.本文根据散度(div(P+,Q+)+div(P-,Q-))|(0,0)的不同情况研究具有反向II型fold-fold的逐段光滑系统(1)所对应的正则系统(5)及其扰动系统的动力学行为.
我们在第2节中给出了一些预备知识及本文的主要结果,并在第3节中给出其证明. 在第4节中, 我们结合例子对主要结果给出一些重要注释.
2 预备知识与主要结果
对于任意一点p:(x,y)∈R2, 如文献[6]定义集合

可知, 当p∈Σ时,F(p)是一个闭凸集. 由文献[6], 一个绝对连续函数ψ(t)若几乎处处满足微分包含式ψ′(t)∈F(ψ(t))则称为逐段光滑系统(1)的解. 从而逐段光滑系统(1)有一个解ψ(t)=(0,0). 然而,对任意初值点(x0,0),x0>0, 其正向轨道先位于下半平面并且与Σ相交于(x1,0),x1<0, 随后进入上半平面, 与Σ相交于(x2,0),x2>0.为了更精确地描述这一现象并且方便计算,我们根据文献[6,13]定义庞加莱返回映射P(x)的等价形式. 当x1∈(-∞,0)时, 定义两个函数

并且当x0,2∈[0,+∞)时定义

那么在Σ上, 等价形式被定义为

进一步,由文献[6]可知, 当P±(x,y),Q±(x,y)∈Ck(k=1,2,…∞,ω)时有P(x)∈Ck. 不妨假设P±(x,y),Q±(x,y)∈Cω.那么可以将P(x)写为
我们采用文献[13]中关于细焦点的阶的定义, 即如果有V1=V2=…=Vk=0但Vk+1>0(<0), 则称点(0,0)为逐段光滑系统(1)的一个k/2阶不稳定(稳定)细焦点. 在此定义下, 虽然逐段光滑系统(1)的焦点(0,0)的阶数可能为分数, 但它统一了解析系统和逐段光滑系统对焦点阶数的定义.
除焦点外, 也可能存在一点(x0,0)∈Σs使得Xs(x0,0)=0, 那么我们将该点称为一个伪平衡点.此时,存在一个解
ψ(t;(x0,0))=(x0,0).
进一步, 如果当x≠x0时(x-x0)Xs(x,0)的第一个分量小于0,且
Q+(x0,0)<0,Q-(x0,0)>0,
则称(x0,0)是一个稳定的伪结点. 如果当x≠x0时(x-x0)Xs(x,0)的第一个分量大于0,且
Q+(x0,0)>0,Q-(x0,0)<0,
则称(x0,0)是一个不稳定的伪结点.此时我们考虑逐段光滑系统(1)的一个扰动, 即令Q-(x,y)=Q-(x-δ,y).那么,当δ>0且足够小时, 由文献[6,14]可知, 逐段光滑系统(1)的(0,0)会分散为上子系统(2)的切点(0,0)和下子系统(3)的切点(δ,0),会产生滑行区域
Σs={(x,0)|x∈(0,δ)}
和滑行向量场. 若滑行向量场有一个伪结点, 并且伪结点和未扰动逐段光滑系统(1)的焦点具有不同稳定性, 穿越极限环就会产生. 当δ<0且足够小时, 情况是类似的. 这类现象被称为伪Hopf分岔或逐段光滑系统的Hopf分岔.
在时间尺度变换及此类扰动下, 正则系统为
由于正则系统与逐段光滑系统在|y|≥ε的区域具有相同的轨道结构, 我们对正则系统的研究主要考虑带状区域R. 对未扰正则系统(6)δ=0, 即正则系统(5), 我们的得到如下结果.
定理2.1当
(div(P+,Q+)+div(P-,Q-))|(0,0)≠0
时存在ε0>0,使得对任意ε∈(0,ε0)正则系统(6)δ=0在(0,0)处具有一个粗焦点. 进一步, 当
(div(P+,Q+)+div(P-,Q-))|(0,0)>0(<0)
时此粗焦点不稳定(稳定).
对扰动正则系统(6), 我们有
定理2.2如果(div(P+,Q+)+div(P-,Q-))|(0,0)>0, 则当δ≠0足够小时扰动正则系统(6)在(0,0)的小邻域内有唯一平衡点且如图 2a所示.
(i) 当δ>0时, 存在(δ,ε)空间中两条曲线ε1(δ)和ε2(δ)满足ε2(δ)>ε1(δ)以及:当ε<ε1(δ)时此平衡点为一个稳定的正常结点;当ε=ε1(δ)时此平衡点为一个稳定的退化结点;当ε1(δ)<ε<ε2(δ)时此平衡点为一个稳定的粗焦点;当ε=ε2(δ)时此平衡点为一个阶数不小于1的细焦点;当ε>ε2(δ)时此平衡点为一个不稳定的粗焦点.
(ii) 当δ<0时, 存在(δ,ε)空间中一条曲线ε3(δ)满足:当ε>ε3(δ)时此平衡点为一个不稳定的粗焦点;当ε=ε3(δ)时此平衡点为一个不稳定的退化结点;当ε<ε3(δ)时此平衡点为一个不稳定的正常结点.
定理2.3如果(div(P+,Q+)+div(P-,Q-))|(0,0)<0, 则当δ≠0足够小时扰动正则系统(6)在(0,0)的小邻域内有唯一平衡点且如图2b所示.

图2 原点附近的参数空间(δ,ε)
(i) 当δ<0时, 存在(δ,ε)空间中两条曲线ε4(δ)和ε5(δ)满足ε5(δ)>ε4(δ)以及:当ε<ε4(δ)时, 此平衡点为一个不稳定的正常结点;当ε=ε4(δ)时此平衡点为一个不稳定的退化结点;当ε4(δ)<ε<ε5(δ)时此平衡点是一个不稳定的粗焦点;当ε=ε5(δ)时此平衡点为一个阶数不小于1的细焦点;当ε>ε5(δ) 时此平衡点为一个稳定的粗焦点.
(ii) 当δ>0时, 存在(δ,ε)空间中存在一条曲线ε6(δ)满足:当ε>ε6(δ)时此平衡点为一个稳定的粗焦点;当ε=ε6(δ)时此平衡点为一个稳定的退化结点;当ε<ε6(δ)时此平衡点为一个稳定的正常结点.
由于函数φ(s)有无数种选取方式,且正则系统的动力学紧密依赖于它, 我们在定理2.2和定理2.3中给出了细焦点阶数的下界,但不能确定细焦点的具体阶数. 我们将会在后面的例子中展示对不同的函数φ(s), 细焦点的阶数是可以超过这两个定理给出的下界.
3 主要结果的证明
定理2.1的证明 不失一般性, 我们对上子系统作时间尺度变换
dτ=-P+(0,0)dt/P-(0,0).
此时有
从而
这样的变换不改变穿越区域、滑行区域以及伪平衡点的类型和稳定性. 因此, 我们对逐段光滑系统(1)不妨假设
P+(0,0)=-P-(0,0)>0.

不难计算出(0,0)为正则系统(6)δ=0的平衡点. 那么对应的雅可比矩阵为
其特征多项式为
λ2-b1λ+b2-b3=0, 这里



因此, 我们得到特征值:

所以,若
则平衡点是不稳定的粗焦点(稳定).定理得证.
定理2.1表明,在散度条件约束下, 正则系统(6)是局部结构稳定的.然而,逐段光滑系统(1)却是结构不稳定的, 并且前文已经说明它可能会发生伪Hopf分岔. 此时,一个很自然的问题是扰动正则系统(6)会不会发生Hopf分岔?定理2.2和定理2.3回答了此问题, 我们在下面给出它们的证明.
定理2.2的证明 定义函数


由定理2.1, 当δ=0且ε足够小时, 在(x,y,δ)=(0,0,0)处有初值条件
κ1(0,0,0)=0,κ2(0,0,0)=0
和行列式

其中
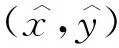
其中




将ai(δ,ε)关于δ在δ=0处进行泰勒展开,得到
a1(δ,ε)=a11(ε)+a12(ε)δ+O(δ2),
a3(δ,ε)=a31(ε)+a32(ε)δ+O(δ2),
进而,再将系数aij(ε)关于ε在ε=0处进行泰勒展开得到
a1(δ,ε)=(a111+O(ε))+(a121+O(ε))δ+
O(δ2),
O(δ2)},
a3(δ,ε)=(a311+O(ε))+(a321+O(ε))δ+
O(δ2),
(a421+O(ε))δ+O(δ2)},
其中








从而在δ与ε足够小时我们得到a2(δ,ε)>0,a3(δ,ε)<0,其特征多项式为
λ2-(a1(δ,ε)+a4(δ,ε))λ+a1(δ,ε)a4(δ,ε)-
a2(δ,ε)a3(δ,ε)=0.
定义函数

4a1(δ,ε)a4(δ,ε)+4a2(δ,ε)a3(δ,ε).
将前面的展开式代入后可得
由于


那么
(a111+a411)ε+a421δ+O(ε2,δ2,εδ).


下证ε2(δ)>ε1(δ), 即对任意的满足H(δ,ε)≥0的(δ,ε)有G(δ,ε)<0. 我们采用反证法.假设ε2(δ)≤ε1(δ).根据定理2.1可知, 可以选取某一(δ,ε),使得H(δ,ε)>0而G(δ,ε)<0.此时,保持δ>0不变而令ε变小, 那么根据前文的讨论和假设可知, 必然存在点(δ,ε)使得
H(δ,ε)=G(δ,ε)=0
或
H(δ,ε)>0且G(δ,ε)>0.
前一种情况对应ε2(δ)=ε1(δ)而后一种情况对应ε2(δ)<ε1(δ).下面我们分别讨论.
对于前一种情况, 函数
G(δ,ε)=-4(a1(δ,ε)a4(δ,ε)-
a2(δ,ε)a3(δ,ε))=0.
但是,将前文中的ai,i=1,2,3,4的展开式代入后可得
这与假设是矛盾的.
对于后一种情况, 我们可以取(δ,ε)足够靠近(δ,ε2(δ))并且G(δ,ε)>0, 使得H(δ,ε)>0且足够小.此时
O(δ,ε))<0.
这与假设矛盾. 命题得证.
G(δ,ε)>0,H(δ,ε)<0.
G(δ,ε)=0,H(δ,ε)<0.
因此特征值为一对相同的负实数.又因为
经过初等行变换后变为
当ε>ε1(δ)且ε<ε2(δ)时, 有
G(δ,ε)<0,H(δ,ε)<0.
G(δ,ε)<0,H(δ,ε)=0.
G(δ,ε)<0,H(δ,ε)>0.
当δ<0时, 曲线ε3(δ)的存在性和平衡点类型以及退化程度的证明是类似的. 这里我们省略其证明.证毕.
定理2.2表明,在散度条件下,在参数空间中确定了平衡点类型变化的临界曲线和焦点阶数变高的曲线. 通过对比,我们发现, 逐段光滑系统(1)在δ的扰动下伪平衡点的类型直接从焦点转化为结点.其主要原因是δ只会影响下子系统.因而我们可以认为这是参数对逐段光滑系统(1)的部分扰动. 然而,在正则系统(6)中,δ的变化是对整个系统产生影响的, 且ε也会带来影响.
定理2.3的证明 与定理2.2中类似, 在δ与ε足够小时, 可以通过隐函数定理得到正则系统(6)的平衡点
+O(ε2))δ+O(δ2)),
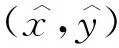
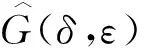

4 例
考虑如下平面逐段光滑系统:
直接计算可得
(div(P+,Q+)+div(P-,Q-))|(0,0)=1.
通过时间尺度变换t→2t, 其正则系统可写为
特征值为
因此,(0,0)是一个不稳定的粗焦点. 这与定理2.1的结果相吻合. 当δ>0时, 平衡点位于

从而可得特征多项式
以及相应的特征值
定义函数

ε2(δ)=φ′δ+O(δ2).
另一方面,定义函数

同理,当δ<0足够小时, 得


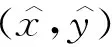
其特征值为
为计算其焦点量g3, 先假设正则函数φ(s)在s=0附近形式为
φ(s)=φ1s+φ3s3+h.o.t.,
其中φj表示sj的系数. 由文献[15],计算可得
其中

C4(δ)+C5(δ),

根据正则函数φ的假设又有