发掘隐性信息 拓宽解题思路

周银生

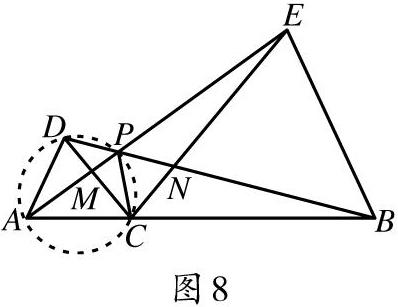
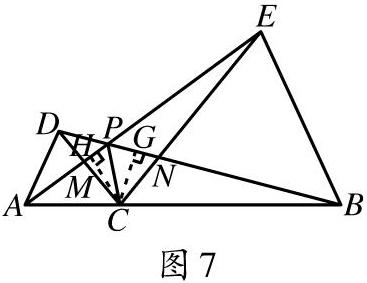
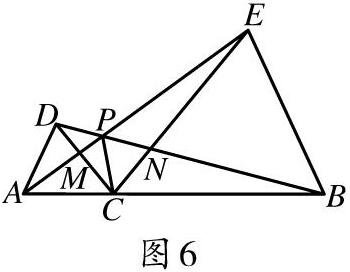
[摘 要]有关“隐圆”的问题是近年考试中常考的内容，需要引起教师的重视.所谓“隐圆”通常体现的是“四点共圆”的问题.在解决若干点相对位置的问题中找出隐含条件，发现“隐圆”，有助于打开思路、找到破题点.

[关键词]四点共圆;平面几何;隐性;解题

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）29-0018-03

初中阶段的平面几何，主要是要求学生掌握常见几何图形的边边之间、角角之间和边角之间的關系.圆是平面几何中的一个主要考点，其内部、边界上和外部的角、边之间具有很多关系.可以利用圆的相关性质进行快速判定，特别是“隐圆”特性形成的新解题思路值得我们探讨.

一、形成“隐圆”（“四点共圆”）的基本条件

由圆的基础定义可以得到，圆上的任意一点到圆心的距离是相等的.反过来说可以理解为确定一个固定点，所有到这个定点的距离相等的点都在同一个圆的边界上，这是“四点共圆”理论的定义起点，也是一切解题思路的出发点，这个条件可以衍生出以下几个具有代表性的问题，需要我们进一步研究和思考.

该方法的运用与学生通常利用的角的相互转化来证明角相等的方法较为适应，顺应了学生的解题思路，降低了该题的分析难度.而关键的要点在于找到共同的圆所在，这就要对“隐圆”的条件和圆有关的特性知识点进行全面的掌握和理解.

初中生在做题过程中要做到思维开阔，对定理和知识要烂熟于心，要对“隐圆”两个条件的推导过程和结论熟练掌握，在遇到证明公共边的三角形或四边形角相等的问题时，有意识地考虑是否可用到“隐圆”，这样对解题思路的破解有一定的帮助.

[   参   考   文   献   ]

[1]  仲惟超.发掘隐性信息，开拓解题思维：以平面几何问题中的“隐圆”为例[J].数学学习与研究，2019（22）：149+151.

[2]  戴娟.微专题在中考数学二轮复习中的实践与思考：以“探寻与隐圆有关的最值与路径问题”为例[J].中学数学月刊，2018（11）：23-25.

[3]  王弟成.高中数学“隐圆”问题的特点与解法：以一道高二学业质量调研试题为例[J].教育研究与评论（中学教育教学），2019（6）：48-52.

[4]  竺宝林.基于“策略与方法联想”的高三习题讲评模式的尝试：以一道南京市期初调研试题为例[J].中小学数学（高中版），2018（10）：48-50.

（责任编辑 黄桂坚）