一类不确定广义系统故障估计的有限时间鲁棒观测器设计

梁天添，刘 鑫，郑 祥，李科信，王 茂

（1. 大连交通大学 自动化与电气工程学院，大连 116028； 2. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

广义系统，又称奇异系统，因其不仅具有微分方程所描述的动态特性，而且具有代数方程所描述的静态特性，故受到学者广泛关注。其中，其故障诊断问题[1-3]是当前的研究热点之一。在广义系统的故障诊断领域内，故障估计不仅能够有效辨识故障的特性、大小，而且能够为容错控制提供基础[4]，因此，针对广义系统故障估计的研究尤为重要。当系统中存在不确定性、未知扰动等未知因素时，如何设计适当的残差生成器，以降低这些因素对故障估计精度的影响，尤其值得关注。

目前，针对不确定广义系统故障估计的研究，较为常见的方法是设计故障估计滤波器/观测器。在故障估计滤波器的设计领域，基于前期研究[5]，作者已针对具有状态不确定性的非线性不确定广义系统，提出了强跟踪故障估计滤波算法；但引入的强跟踪渐消因子具有次优特性，在解决系统不确定性问题上具有一定的保守性。在故障估计观测器的设计领域，文献[6]针对具有未知输入的不确定广义切换系统设计了降阶观测器；文献[7]基于不确定广义系统模型，针对具有系统故障的高速列车牵引系统三相逆变器的故障估计问题，设计了自适应观测器，但是在求解过程中引入了未知变量，导致观测器限制矩阵存在非凸问题；文献[8]针对不确定线性时不变广义系统，利用状态变量参数化的方法设计了故障估计观测器。

上述文献针对广义系统故障估计问题的研究，均只考虑了系统的渐进稳定性，而对于如飞行器姿态控制系统[9,10]、电力系统暂态分析[11]等实际控制系统，需更多关注特定时间内系统的行为。此外，对于短时间内发生的微小故障，需要在特定时间范围内进行估计，以保证实际系统安全地运行。因此，在有限时间范围内研究广义系统的故障估计问题，更具现实意义。目前针对状态空间系统有限时间故障估计问题的研究，已经取得了一定的进展[12-14]，但在广义系统领域仍然有限。尽管已经有一些学者针对广义系统的有限时间故障估计问题，提出了观测器的设计方法[15-17]，但这些观测器结构均是奇异的，具有计算量大、实现困难等不足。

针对上述文献中存在的不足，基于前期研究[18]，本文基于一类满足Lipschitz 条件的不确定非线性广义系统，即卫星姿态控制系统(Attitude Control Systems, ACSs)，提出了一种故障估计观测器设计方案。该观测器的优点如下：首先，考虑了系统不确定性对于系统建模的影响，拓展了广义系统有限时间故障估计理论；其次，设计的观测器具有非奇异结构，结构简单、便于计算及实现。最后，设计的观测器不仅保证增广误差系统动态方程满足有限时间有界(Finite Time Boundness, FTB)条件，而且保证故障估计误差对于扰动满足有限时间鲁棒H∞条件。

本文内容安排如下：首先，针对不确定广义系统故障模型，视故障为部分系统状态变量，不确定性为系统的增广扰动，建立增广系统模型。其次，设计有限时间故障估计观测器，该观测器具有非奇异结构；进而，建立增广误差系统模型。然后，分析误差系统的FTB 性能，讨论故障估计误差对于扰动的鲁棒性。再次，给出观测器增益限制矩阵存在的充分条件及该限制矩阵的线性矩阵不等式（Linear Matrix Inequality, LMI）形式。最后，给出一个卫星ACSs 模型，考虑系统执行器发生缓变故障（飞轮漂移故障），传感器（陀螺）发生突变故障，利用设计的有限时间鲁棒观测器（Finite Time Robust Observer, FTRO）仿真，并与以往文献中基于渐进稳定的故障估计方法进行对比分析，以验证所提出方法的有效性。

1 增广系统建模

考虑如式(1)所示的不确定广义系统：

其中， x ( t )∈Rn为状态向量， u ( t )∈RP为系统输入，fx(t)∈Rq为系统故障，w (t )∈Rw表示外部扰动，Φ ( x)为系统的非线性项， y ( t )∈Rm为系统输出，ΔA、ΔB分别为系统的不确定性，A、B、C、D 和Fx为具有适当维数的已知系数矩阵。

为保证广义系统(1)的可观性，提出如下假设： 假设1 系统(1)满足如下条件：

假设2 不确定性ΔA，ΔB 满足：

其中，Mi，Ni均为具有适当维数的已知系数矩阵，未知矩阵Fi(t)满足( t ) Fi( t) ≤I, i=1,2。

假设3广义系统(1)中的非线性项 Φ ( x)满足Lipschitz条件，即存在κ ＞ 0，使得式(6)成立：

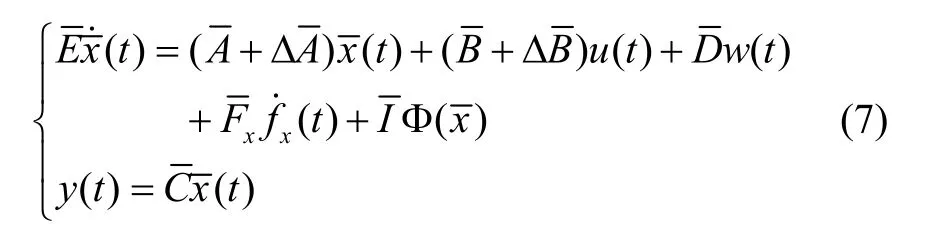
注释1本文中，增广广义系统(7)中的状态变量控制输入 u (t)，干扰w(t)以及执行器故障的导数满足：为给定的正标量，T 为有限时间窗的终止时刻。

2 故障观测器设计

针对广义系统(7)，设计如式(8)所示的FTRO：

其中，ζ (t)∈Rn+q表示观测器的中间变量，表示状态估计向量，G、N 和L 为待设计的系数矩阵。

首先给出与推导及证明相关的定义及引理。 定义1[19]给定标量 c1＞ 0，T ＞ 0，矩阵R ＞ 0，系统(10)关于(c1，c2，T，R，d)是FTB 的，如果：

其中，t∈[0, T]为有限时间窗，T 为有限时间窗的终止 时刻，w(t)满足：为一个正实数。

引理1[20]若式(2)和(3)成立，则存在一个非奇异矩阵G和矩阵N 满足：

引理2[20]对于满足引理1 的非奇异矩阵G 和矩阵N，其通解为：

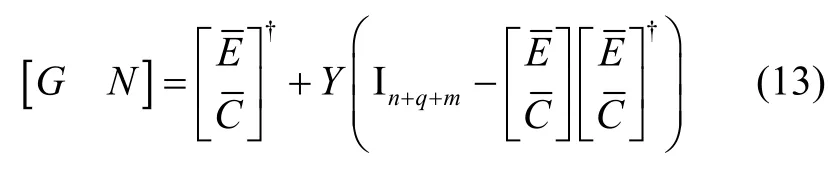
其中，Y 为任意矩阵，代表设计自由度，†表示伪逆。

引理3[14]给定正标量ε，矢量x 和y，对于适当维数的任意实矩阵B1、C1和D1，若有则有：

本文的设计目标为：设计FTRO，使得增广误差系统(9)满足如下条件：

1） e(t )关于( c1, c2, T , R , xa, ua, d , fa)是FTB 的；

2）故障估计误差 ex( t )对于外部干扰、执行器故障导数及系统不确定性具有鲁棒性，即：

定理1 用于保证条件1）成立。

定理1给定标量κ ＞ 0，c1＞ 0，γa＞ 0，γu＞ 0，γw＞ 0，γx＞ 0，α＞ 0，若存在正定对称矩阵P∈R(n+q)×(n+q)，矩阵W∈R(n+q)×n，使得：

其中，Q=R-1/2PR-1/2，则增广误差系统(9)中 e(t )关于( c1, c2, T , R , xa, ua, d , fa)是FTB 的。

证明：选取如下形式的Lyapunov 函数：

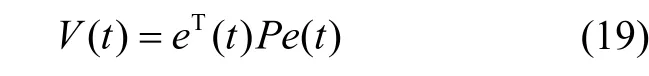
由式(9)中第一个等式及式(19)可得：

其中，He{* }= {* }+ {* }T。

由引理3 可知，式(20)中不确定性及非线性项满足：

又ΔΦ 满足Lipschitz 性质，即：

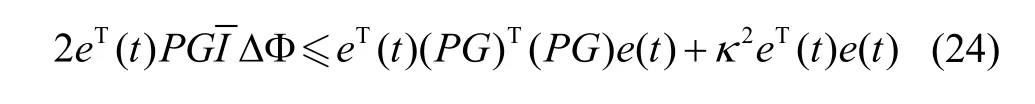
由不等式(21)-(24)可知：

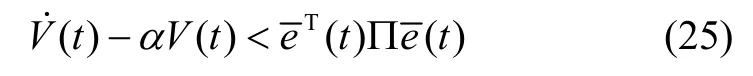
其中：

令W =PL，根据舒尔补引理，由式(16)可知：

通过计算可得：

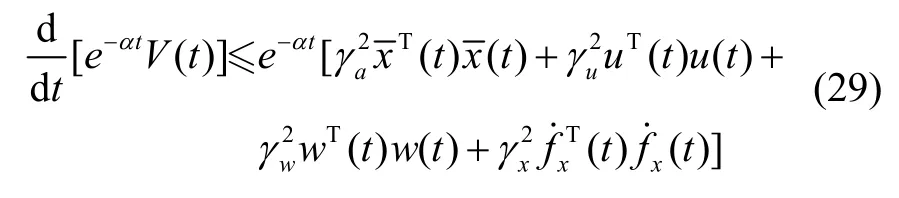
对式(29)从0 到T 积分，则有：

注意到：0＜e-αt＜ 1，则式(30)满足如下关系：

λmax( Q)和 λmin( Q)分别表示矩阵Q 的最大和最小特征值，将式(31)-(33)代入式(30)可得：

由式(18)可知：

式(35)符合定义1，定理1 证毕。

为进一步分析增广误差系统(9)的有限时间鲁棒H∞性能，给出定理2 中相关内容。

定理2对于增广误差系统(9)，给定标量γa＞ 0，γu＞ 0，γw＞ 0，γx＞ 0，α ＞ 0，若存在正定对称矩阵P∈R(n+q)×(n+q)，矩阵W∈R(n+q)×n，使得：

证明：定义如式(37)所示的指标函数：

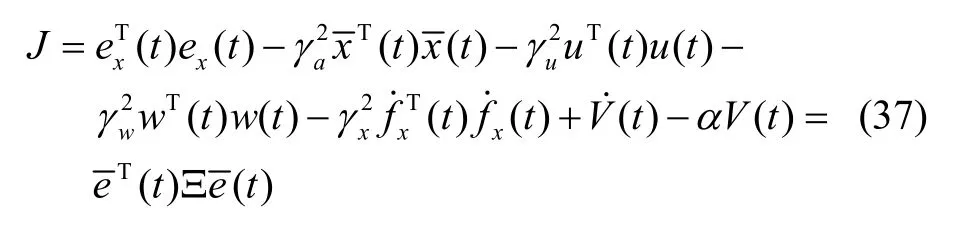
易知当Ξ＜ 0时，有J ＜ 0。

进一步，由舒尔补引理可知，式(37)与式(36)具有等价关系。注意到：

则当Ξ＜ 0时，式(27)成立。由定理1 中推导可知，若式(36)(17)及(18)成立，则条件1）得到满足。

对式(37)从0 到T 积分，通过计算可得：

注意到 V ( t ) ＞ 0，则有：

即，若式(36)(17)及(18)成立，则条件2）得到满足。

经上述推导可知，若有式(36)(17)及(18)成立，则条件1）和2）同时得到满足，定理2 证毕。

结合上述内容，给出如算法1 所示的不确定广义系统执行器故障估计FTRO 设计流程。

算法1FTRO 设计流程。

步骤1：选择式(13)中的自由度Y，得到G 和N 值。

步骤2：给定c1，c2，T，R，xa， ua，d 和 fa。

步骤3：解下列约束问题：

步骤4：求解观测器增益矩阵L =P-1W。

步骤5：得到故障估计值：

3 仿真算例

本节给出一个如式(41)所示的卫星ACSs 模型：

其中，ωx，ωy和ωz分别表示偏航轴、俯仰轴和滚转轴的转动角速度，Ux、Uy和Uz分别表示不同轴的控制力矩，Tdx、Tdy和Tdz分别表示空间环境干扰力矩，Ix、Iy和Iz分别表示转动惯量，取值如表1 所示。

表1 转动惯量参数Tab.1 Parameters of moment of inertia

假设模型中同时存在执行器故障(飞轮斜坡漂移)fx( t)(N · m)和传感器(陀螺)突变故障 fy( t ) (rad/s)，其 分布矩阵分别为Fdx=［10 0］T，Fdy=［ 01 0］T。

注释2本节中，首先将传感器故障视为系统状态变量，建立广义系统模型。进而，将执行器故障视为增广状态变量，建立符合式(7)的增广广义系统模型。基于该建模方法，设计的观测器不仅可以基于广义模型(1)估计出系统的执行器故障，还能同时估计出系统的传感器故障。

给定κ=0.1，根据定理2，经仿真计算可知，c2值随着α 的增大而增大，而 γa、 γu、 γw和 γx的值随着α 值的增大而减小，且在α＞ 4后 γa、γu、γw和 γx的值趋于定值。因此，折衷考虑观测器的估计精度和系统鲁棒性，给定 α =3.6，此时得到 γa、γu、γw和 γx的最小值为γa=0.12，γu=0.016，γw=0.13，γx=0.2。由定理2 计算得到的观测器系数矩阵L 为：

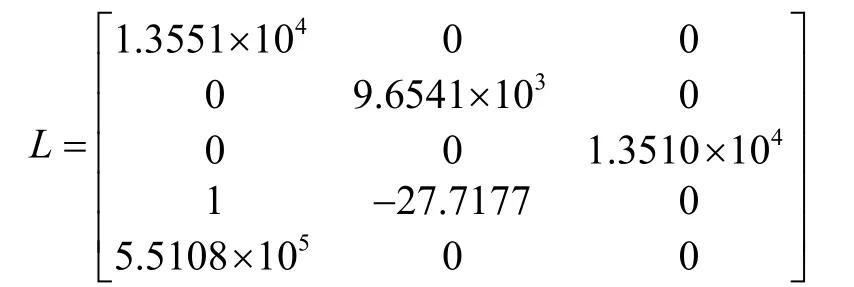
为验证设计方案的有效性，利用本文设计的FTRO 与文献[20]中指数稳定观测器(Exponential Stability Observer，ESO)进行对比仿真。当系统发生故障时，状态变量及故障估计结果如图1及图2所示。状态估计及故障估计均方根误差（Root Mean Square Error, RMSE）如表2 及表3 所示。

图1 发生故障时状态变量及其估计结果Fig.1 State variables and their estimations when faults occur

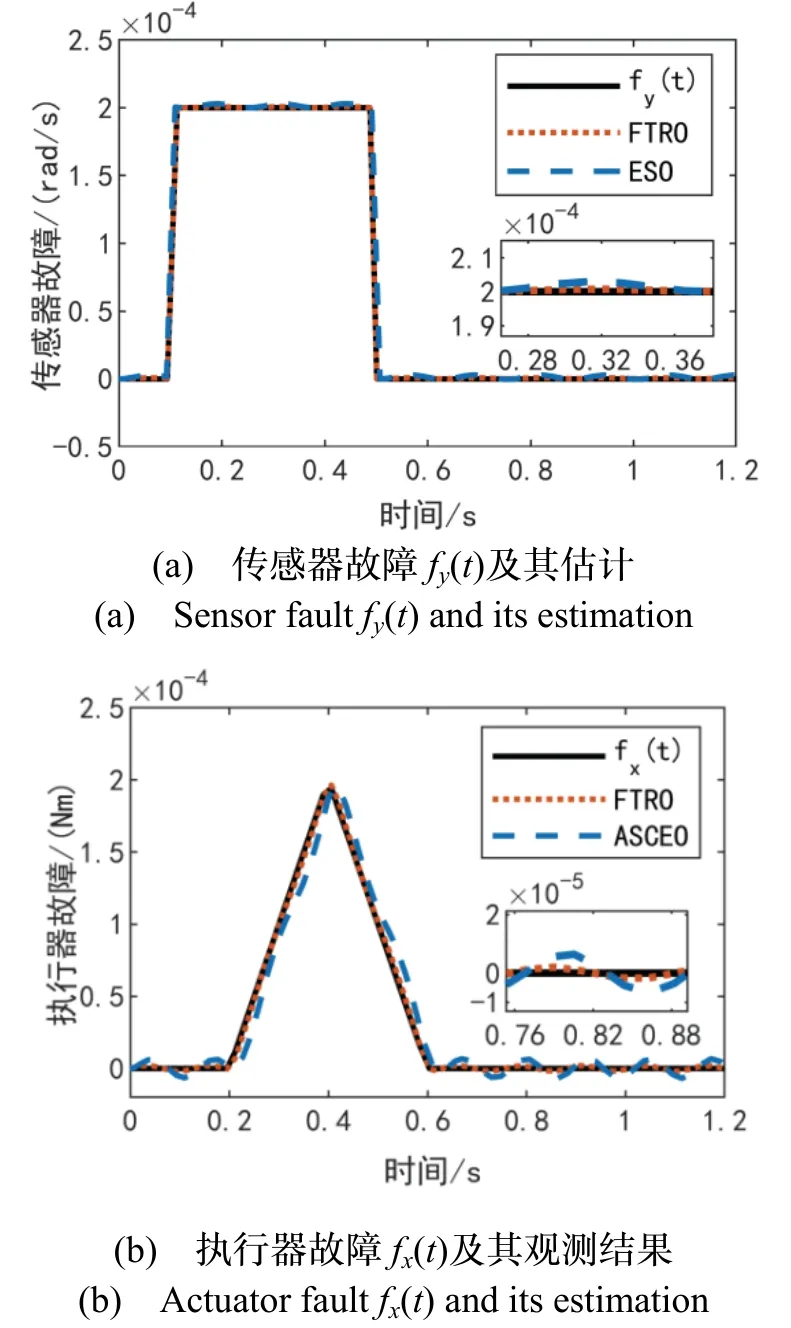
图2 故障及其估计结果Fig.2 Faults and their estimation results

表2 状态变量估计误差（RMSE）Tab.2 RMSE of state variables estimation

由图1 及图2 可知，当系统存在不确定性及未知扰动时，本文设计的FTRO 相较于ESO，不仅能够更好地估计出故障的真实值，而且能够更精确地估计出发生故障时的系统状态值，表2 及表3 进一步验证了其精确性。从表中可知，相较于ESO，FTRO 对于状态变量的估计误差RMSE 分别降低了80.6%、25.3%和 47.5%；对于传感器和执行器故障的估计误差RMSE 分别降低了53.4%和75.5%。仿真结果表明，基于广义系统模型，利用提出的FTRO，不仅可以有效估计卫星ACSs 发生的执行器故障及传感器并发故障，而且能有效地估计出耦合于故障的系统状态值。即，基于广义系统模型，在存在不确定性及未知扰动的情况下，设计的FTRO 仍能在有限时间内实现有效的并发故障估计。仿真验证了设计方案的有效性。

表3 故障估计误差（RMSE）Tab.3 RMSE of faults estimation

尽管如此，本文研究方法仍有进一步改进空间，如真实卫星ACSs 中通常存在一定的状态时滞，该时滞环节对故障估计的实时性及准确性均有不可忽视的影响。众所周知，自适应算法可以实现快速的状态/故障估计。因此，基于不确定时变时滞广义系统模型，研究卫星ACSs 的自适应有限时间鲁棒故障估计方法，以便在有限时间内快速准确估计系统故障，具有理论和现实意义。

4 结 论

本文针对一类不确定非线性广义系统的故障估计问题，提出了一种FTRO 设计方案。建立了增广误差动态系统，设计了非奇异结构的故障估计观测器，给出了满足FTB 条件及有限时间鲁棒H∞条件观测器增益限制矩阵的LMI 形式，并利用对比仿真验证了设计方案的有效性。仿真结果表明，基于不确定广义系统模型，针对卫星ACSs 的并发执行器、传感器故障及耦合于故障的系统状态变量，设计的FTRO 均能在有限时间内精确估计其真实值。本文的研究方案可为后续不确定时变时滞广义系统的自适应有限时间故障估计提供理论基础。