超高灵敏度加速度计温度模型测试方案与实验

张梦琪，刘金全，刘丹丹，王 秋，刘骅锋，涂良成

（华中科技大学物理学院引力中心，重力导航教育部重点实验室，武汉 430074）

作为惯性测量系统核心元器件之一的加速度计，当其分辨率达到ng (1 ng=10-9g，g 为当地重力加速度)量级时，可应用于微震和重力场的测量，涉及资源勘探、重力辅助导航和空间探索等需要高精度加速度传感器的领域[1-5]。此类加速度计分辨率比较高，在使用环境的温度产生变化时，由于组成材料或信号提取电路的性能会随之产生变化，输出对于环境温度比较敏感，一定程度上制约了其测量精度的提升，限制了使用场合[6,7]。

对加速度计温度特性进行表征的方式通常是建立加速度计的温度模型，主要表现在零偏的温度灵敏度和标度因数的温度灵敏度两方面[8,9]，可以先测试得到两个系数然后通过补偿的方法对其进行校正，以降低加速度计的温度灵敏度[10-13]。这就需要对加速度计本身的温度特性进行充分、准确的测试。通用的温度特性测试方法是把加速度计安装在温控箱内，对加速度计进行升降温试验[14-16]，结合重力场分度装置[17,18]或者精密离心机测试[19]不同温度点下加速度计的输出，然后关于温度做最小二乘拟合，从而得到加速度计温度模型中的各项系数。然而对于ng 级加速度计，因为加速度计分辨率高，远小于1″的姿态改变即可能影响到加速度计的输出，温度变化时夹具等产生的微小热形变即可能干扰温度灵敏度的测量，为温度特性的检测带来难度。

本文针对ng 级超高灵敏度加速度计[20,21]温度特性的测试，详细分析了利用重力场分度装置测试时存在的潜在误差及其影响，确认了利用典型重力场进行此类加速度计温度灵敏度系数标定的可行性，并利用重力场中小角度倾斜四位置旋转的方法，基于带温箱的二轴温箱对本实验室研制的ng 级高精度MEMS 加速度计温度模型进行了测试，将此温度模型用于星载试验数据的温度补偿，结果表明，此方法对于改进加速度计在高精度应用场景中的特性是有效的。

1 加速度计温度模型

根据相关的国际和国内标准[22,23]，加速度计的输出E 可表示为沿其基准轴作用的加速度等输入的数学关系式。本文中以其简化的模型为例，此时加速度计门状态安装时输出E 和沿输入敏感轴的加速度ai的关系可表示为：

其中K0表示加速度计的零偏，K1表示加速度计的标度因数。根据本课题组前期的工作结果，超高灵敏度加速度计在重力场测试中高阶项的激发效果较弱[24]，其对温度模型测试的误差贡献将在章节3.4 中进行讨论。

根据文献[2]，加速度计的模型参数零偏K0和标度因数K1关于温度的模型可以由如下函数关系表示：

温度灵敏度系数和温度的函数关系可以采用多种形式，例如，公式(2)中的K0(Tj)和K1(Tj)可以具化为多项式，当仅考虑它们关于温度的线性关系时，加速度计含温度模型的输出可以表示为

其中，Tj是不同的温度点，a0和a1分别是室温条件下加速度计的零偏和标度因数，b0是加速度计零偏关于温度的线性响应系数，b1是加速度计标度因数关于温度的线性响应系数。

本文重点关注在不同温度点下如何对加速度计的零偏K0和标度因数K1进行准确测试。

2 温度模型参数测试潜在的问题

为了对加速度计的零偏灵敏度和标度因数灵敏度进行测试，一种简单方便的方式是定点升温法[14]，它利用加速度计在重力场中两个不同姿态位置的输出分别获取零偏和标度因数的温度信息：首先将加速度计置于水平面上，此时加速度计的输出即表征零偏K0(Tj)，改变温度Tj即可测得加速度计的零偏温度灵敏度系数，继而将加速度计置于有较大重力加速度输入的姿态（例如1 g 输入），从加速度计输出中扣除零偏K0(Tj)的贡献，即可得到标度因数K1(Tj)随温度的变化，从而推知标度因数温度灵敏度。这种方法对于分辨率在亚mg 左右的加速度计是可行的，然而对于ng分辨率的加速度计，温度变化很容易引起加速度计夹具和基座的形变，原因可能是材料内部应力改变、各部件热涨系数不匹配或温度不均匀等，最终导致和加速度计敏感结构无关的加速度计输出，效应远超ng，最终干扰对加速度计本身温度系数的测量。如图1 所示，假设因为某种原因加速度计的安装基座产生微小形变，导致敏感轴方向偏离预期的水平方向，偏离的角度为γe，则加速度计的输出为：

图1 定点升温模型图Fig.1 Model diagram of fixed-point temperature-rising tests

在计算此温度点的零偏时，K1(Tj)gsinγe就会耦合在其中。尤其需要注意的是，在不同温度下，由于形变γe的不同，这项误差也可能不同。

在加速度计处于有较大重力加速度输出的姿态时，加速度计的实际输出为：

对于ng 分辨率的超高灵敏度加速度计，受到量程限制，其倾斜角度γ 较小，比如量程为10 mg 的加速度计其敏感轴偏离水平面的倾角最大仅为0.57 °，1″的γe变化，即带来近5 μg 的加速度变化，直接影响到零偏和标度因数温度系数的测试。

因此，简单的二位置变温试验不再适用于ng 级加速度计的温度模型测试。而对于更多位置的测试方法，则需要进行系统的误差分析，确定实验方案的可行性。

3 测试方案与误差分析

3.1 测试方法

从传统的重力场中竖直平面内等角度多位置翻滚的测试方法出发，本文采用在小角度倾斜平面内进行等角度多位置旋转测试。如图 2 所示，加速度计敏感轴（Input Axis, IA）位于旋转平面内，γ 是倾斜的角度，θk=360°×k/n 是旋转的角度，k=0, 1, 2…n-1。沿敏感轴方向的输入分别为gsinγsinθk。当θk=0 时，沿敏感轴方向的输入为0；当θk= π/2 或3π/4 时，沿敏感轴方向的输入分别为±gsinγ。这样一来，沿敏感轴的重力加速度分量最大值从竖直平面内的1g 减小为小角度倾斜平面内的gsinγ，适当选择γ 可以确保加速度计在旋转到不同位置时均处于未超量程的正常工作状态。

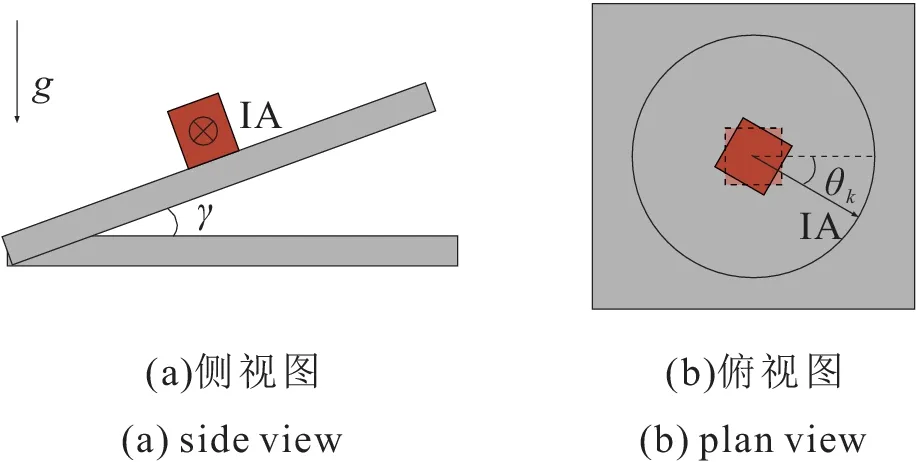
图2 小角度倾斜面内等角度多位置旋转测试原理图 Fig.2 Tilt multi-position angle schematic

此时加速度计的输入为：

根据式(1)，加速度计此时的输出为：

当加速度计模型中仅考虑一阶项及零偏项时，仅存在两个待求系数，故n≥4 即可。以n=4 为例，即从传统的四点翻滚法出发，在倾斜平面内进行等角度四位置定点标定，在这四个位置，加速度计的输出应分别为：

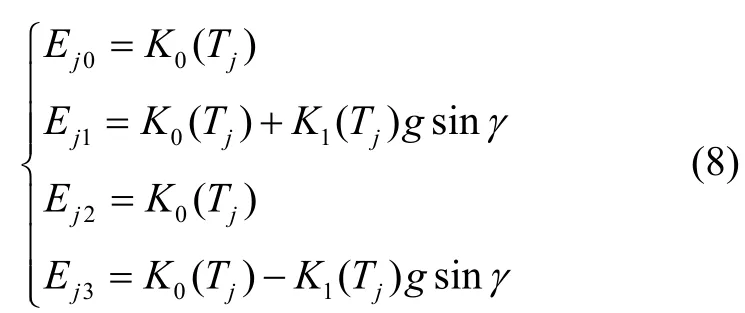
式(8)经过加减组合，就可以得到一组零偏和标度因数：

然后，将各组零偏和标度因数分别与其对应的温度进行拟合，就可以得到加速度计零偏和标度因数各自的温度模型。

3.2 夹具热形变产生的误差角

在某个温度T 下，当存在夹具对应的受热形变时，加速度计敏感轴方向可能从图3 所示的实线箭头方向变化为虚线箭头方向，即该温度下加速度计的实际敏感轴方向偏离其初始安装方向某一个小角度γe1。误差角γe1可能随着温度的变化而发生变化；而在同一个温度点下做多位置旋转时，如果温度场足够均匀则该角度变化可以假设为维持不变，如果温度场不均匀则需要考虑该角度随角位置的改变。还需要注意的是，即便在旋转到不同位置点时输入轴方向出现某种小的偏差，只要该偏差不随着温度和测量时间点的改变而改变，则该偏差对于通过变温来测量温度系数的实验没有显著影响，因此有些固定误差可以不予考虑。

图3 夹具受热形变后加速度计敏感轴方向变化。Fig.3 Changes in the direction of the accelerometer sensitive axis after the fixture is deformed by heat

首先假设定点温度下温度场均匀，因此不同角位置下可以用同一个γe1,，则加速度计的实际输出为：

从式(10)可以看到，其中Ej0和Ej2均包含一个可能较大（相对于 ng 加速度计而言）的误差项K1(Tj)gcosγsinγe1；而Ej1和Ej3的第二项会受到γe1的影响，将其展开为：

当γe1≤2′时，cosγe1造成的相对误差≤0.1 ppm，而γe1≤2′的条件在精密设备中，可以得到很好的保证，所以公式(11)中主要的误差来源是K1(Tj)gcosγsinγe1≈ K1(Tj)gsinγe1（其中，γ 是一个小角度，cosγ 接近于1），这项误差和Ej0、Ej2中的误差项相当，也是一个可能较大的误差项。由此可见，每个位置点上，加速度计的输出均可能包含较大的误差。

对式(11)进行加减组合，则可以推知各个温度测试点Tj下的零偏和标度因数：

式中的“≈”是基于当γe1≤2′时cosγe1造成的相对误差≤0.1 ppm 的前提。

从式(12)可以看到，利用等角度多位置数据求取K1的过程中，对称位置的组合运算巧妙地消除掉了单个位置（定点升温法）测试时较大的误差项，如此可以大幅度提升K1的测试精度。对于零偏K0而言，γe1则会经由K1j贡献到测试结果中，然而，由于本文中关注的是其温度灵敏度，所以一旦K1的温度灵敏度测试准确，即可估算该项误差对于零偏温度灵敏度测试的影响。比如，若标度因数的温度系数≤100 ppm/℃，则当形变 γe1≤2′时，将对零偏温度系数带来≤0.5cosγ μg/℃的误差，也就是说，随着γ 的减小，这项误差会逐渐增大，对于量程10 mg 的加速度计，倾斜角度γ 为0.45 °时，此误差约为0.58 μg/℃。需要说明的是，实际情况中定点温度下温度场一定会存在不均匀，上述理论分析的扣除效果可能会存在一定的偏差。

3.3 分度机构基座倾斜角度波动产生的影响

除了上述的加速度计夹具由于温度改变而造成的局部变化需要考虑，还需要考虑在测试过程中，旋转面整体的倾斜角度因为某种原因产生了波动造成的影响。比如，设备外界环境温度或温度梯度发生了改变，导致设备基座两侧热膨胀程度不同，或者温箱内的温度引起了基座温度的改变，导致设备基座自身的热形变，亦或者倾斜潮汐造成的倾角改变。如图4 所示，在存在分度机构倾斜角度波动造成的误差角γe2时，实线箭头方向变化为虚线箭头方向。用γe2||表示γe2沿θ =0 方向的误差角，γe2⊥表示沿θ = π/2 方向的误差角。

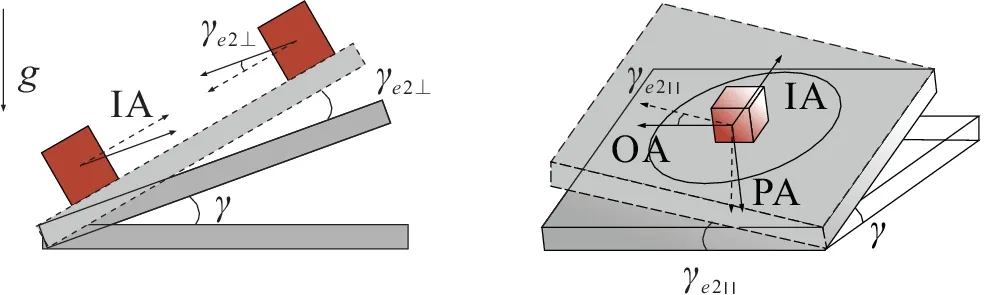
图4 分度机构倾斜角度波动造成的加速度计敏感轴方向变化Fig.4 Changes in the direction of the accelerometer sensitive axis after the dividing mechanism is deformed by heat

此时，加速度计的实际输出为：

式(13)经过加减组合，得到不同温度测试点Tj下的零偏和标度因数：

从式(14)可以看到，经过组合处理后，基座倾角出现的小角度波动不会影响到零偏温度系数的测量，但却会影响到标度因数温度系数的测量。对于量程较小的ng 分辨率加速度计，1″的γe2⊥的变化就将引起几百到上千ppm 的相对误差，因此，如果要准确地测试标度因数的温度系数，需要在整个测量过程中，将倾斜角稳定在远好于1″的水平。这就要求必须对环境温度和温度梯度进行控制，并将倾斜装置设计在常温环境中，减小基座倾斜角波动造成的影响。

另外如果测量持续时间比较长，达到几个小时或更长，则需要考虑倾斜潮汐的影响。倾斜潮汐最大可在±200 nrad 即±0.05″的范围内波动，有可能造成约30 ppm 的相对误差。

综上所述，对于量程仅为mg 量级的超高灵敏度加速度计，要测试其温度模型，需要将倾斜分度机构置于温控机构之外，保持测试设备外界环境的温度稳定，并且采用倾斜至一小角度然后等位置间隔旋转的方式测试不同温度点下的零偏和标度因数，以减小加速度计夹具热形变和基座倾斜波动引入的误差。对于标度因数温度系数≤1000 ppm/℃，并且夹具热形变小于 2′的情况下，零偏温度系数测试精度可优于0.5 μg/℃，标度因数的测试精度主要受限于基座倾斜角度的波动，倾斜潮汐造成的影响最大约为30 ppm。

3.4 加速度计高阶项系数带来的误差

若考虑加速度计的高阶项系数，以二阶非线性系数K2为例，加速度计的输出E(Tj)应为：

在k=0 和2 的位置处，ai=0，K2带来的效应对加速度计输出不构成影响，在k=1 和3 的位置处，K2带来的效应将通过对这两个位置加速度计的输出做减法消除掉，因此二阶非线性系数不会影响加速度计的温度模型测试。

以交叉耦合系数Kip为例，加速度计的输出E(Tj)应为：

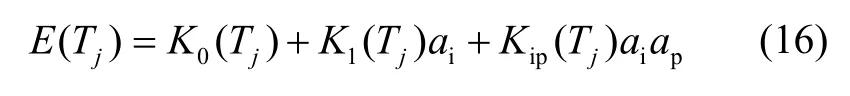
类似地，在k=0 和2 的位置处，Kip带来的效应对加速度计输出不构成影响，而在k=1 和3 的位置处，Kip带来的效应无法通过减法消除掉，最终得到的不同温度测试点Tj下的零偏和标度因数为：

若Kip随温度变化很小或者其本身的效应贡献到加速度计输出上很小，则可以忽略其影响；否则应使用更全面的输出模型，例如式(16)，对加速度计的各个模型参数进行拟合。

4 测试实验与分析

基于以上分析，本实验室采用北京航空精密机械研究所研制的基于双轴转台的变温试验系统进行了温度模型的测试。如图5 所示，测试装置主要包括双轴转台、高低温箱、直流电源和高精度数据采集系统。双轴转台的转角精度达到1″，温箱及内部转动台面可以沿着水平轴做倾斜转动，转动台面可以做360 °旋转，所有转动控制机构在高低温箱之外，温箱的控温精度达到0.1 ℃，温控均匀性优于±2 ℃。整个实验过程中，实验室的温度控制在(23±1) ℃。

图5 实验设备Fig.5 Experimental equipment

4.1 高精度MEMS 加速度计温度模型测试实验

我们以自研高精度MEMS 加速度计为测试对象，对前述方案展开验证。待测MEMS 加速度计的量程为10 mg，分辨率达到3 ng/ Hz，内置温度传感器以便更加准确地评估加速度计的温度。考虑加速度计可能存在的温度效应，倾斜角度γ 设定为0.45 °，旋转θ角时能产生的最大加速度为7.9 mg，略小于加速度计10 mg 的满量程。在倾斜平面内，进行十二位置定点测试。每完成一个温度点的12 点测试后，改变温箱温度，保温1 小时，以使加速度计内部以及设备整体达到均匀的热平衡状态。根据应用需求，我们依次在20～40 ℃之间每隔5 ℃做了5 个温度点的测试，分别求出这五个温度点的零偏和标度因数。

图6 和图7 分别给出了计算出的加速度计零偏和标度因数随温度变化的关系图。图中展示了三次重复升温实验的结果，以及零偏和标度因数分别关于加速度计内部温度变化的线性拟合结果。零偏和标度因数均表现出了与温度较好的线性关系。

图6 零偏关于温度的变化情况Fig.6 Bias as a function of temperature

图7 标度因数关于温度变化情况Fig.7 Scale factor as a function of temperature

通过拟合可以得到，三次实验中零偏的温度模型和系数分别如表1 所示，标度因数的温度模型和系数分别如表2 所示。综合各温度点的多次实验数据，在95%置信区间内，零偏的不确定度达到了0.5 μg/℃，其可能原因是不同温度点下转台确实存在较大的变形，或者因为温度不均匀较大且在不同温度点下温度梯度存在较大的变化；相同的置信区间条件下，标度因数的不确定度达到了4 ppm/℃，各温度点之间标度因数的波动则为～100 ppm，考虑到实验室温度的不确定度为1℃，据此评估基座倾斜带来的影响最大约为6000 ppm，也就是标度因数的波动大于倾斜潮汐带来的影响，小于实验室温度1℃不确定度带来的影响，故实验室温度是影响本实验标度因数不确定度的主要因素。

表1 零偏的温度系数Tab.1 Temperature coefficient of bias

表2 标度因数的温度系数Tab.2 Temperature coefficient of scale factor

通过对各组实验结果分析，可以计算得到零偏的温度系数测试重复性优于0.4 μg/℃（95%置信区间），标度因数温度系数测试重复性优于30 ppm/℃（95%置信区间），达到了良好的测试效果。

4.2 高精度MEMS 加速度计定点升温法对照实验

为与本文所提方法进行对比，我们采用传统的定点升温法对同一只加速度计进行了测试。在将加速度计分别固定在0 输入、正向接近满量程输入、负向接近满量程输入的三个位置，如前述实验在20～40 ℃之间每隔5 ℃改变温箱温度，采集加速度计的输出，以0 输入位置的测试结果表征加速度计零偏的温度系数，如表3 所示。

表3 定点升温法零偏的温度系数Tab.3 Temperature coefficient of bias in different fixed-point temperature

以接近满量程输入位置的测试结果表征加速度计标度因数的温度系数，分别如表4、5 所示。

表4 定点升温法标度因数的温度系数（正向）Tab.4 Temperature coefficient of scale factor in different fixed-point temperature (positive direction)

表5 定点升温法标度因数的温度系数（负向）Tab.5 Temperature coefficient of scale factor in different fixed-point temperature (negative direction)

从零偏温度系数的测试结果可以看出，定点升温法和本文提出的方法结果一致，但对于标度因数温度系数的测试而言，定点升温法表现出了非常大的弊端：在加速度计正向和负向满量程输入时结果差异很大，这主要是由于夹具随温度发生了单向的形变γe1，K1(Tj)gsinγe1中γe1随温度的变化被当做了标度因数随温度的变化，与正向输入和负向输入时的测试结果分别叠加或抵消，从而使结果表现出不一致，这也证明了消除夹具形变误差角的必要性。

4.3 星载MEMS 加速度计温度模型测试与补偿

为再次验证本文提出的方法，我们对一款量程为2 mg 的自研星载MEMS 加速度计进行了三组测试，可以得到标度因数的温度系数为1831 ppm/℃，不确定度为247 ppm/℃，各温度点之间标度因数的波动则为～4700 ppm，大于潮汐引起的波动(231 ppm)，根据章节3.3 的分析，倾斜0.06 °测试时，由于倾斜角度γ太小，分度机构倾斜角度的波动影响被放大了，实验室温度梯度变化导致的基座倾斜成为影响测试精度的主要限制条件；零偏的温度系数为44 μg/℃，不确定度为5 μg/℃，各温度点之间零偏的波动为～120 μg，大于理论波动1 μg，仍考虑这是转台变形或温度梯度导致的。

对其星载试验的结果[25]，依据地面温度测试结果，对其进行了补偿，结果如图8 所示。可以看到，在存在如绿色曲线所示的较大温度变化趋势时，未经温度补偿的加速度计输出也表现出了和温度较大的变化趋势，在温度趋于平稳时，加速度计的输出变化也随之趋于平缓，表现出了较强的相关性，系数可达47 μg/℃，而经过温度补偿的加速度计输出则摆脱了和温度相关的变化趋势，降低为1.7 μg/℃，为补偿前的3.5%，有效减弱了温度对加速度计输出的影响。

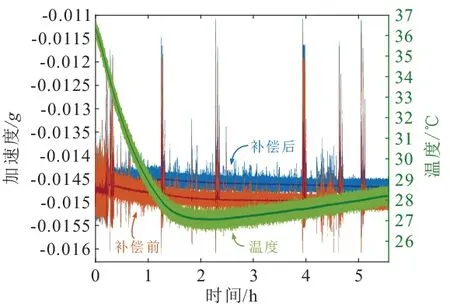
图8 高精度MEMS 加速度计星载过程中温度补偿前后的加速度计输出Fig.8 Acceleration output of high precision MEMS accelerometer before and after temperature compensation in spaceborne test

5 结 论

本文从ng 级MEMS 加速度计的测试需求出发，全面地分析了超高灵敏度加速度计的零偏和标度因数的温度系数测试时面临的误差，量化了各误差带来的影响，从原理上给出了重力场多位置测试方案中提升测试精度的方法，并确认部分误差依然可通过在重力场中选取对称位置进行多位置测试予以抵消。对本组自研的ng 级加速度计进行了测试，试验结果表明，对于ng 级的加速度计，其零偏和标度因数的温度系数测试精度主要受限于倾斜潮汐等地面环境波动的影响，在可以保证加速度计精度的情况下，适当增大其量程，或控制实验设备外部温度，从而减小地面倾角波动，将有效提高标度因数的温度系数测试精度。本分析亦可适用于部分微震仪、倾斜仪的温度模型测试。