中低纬度评估极区导航时IMU数据转换误差模型

卞鸿巍，文 者，马 恒，王荣颖

（海军工程大学电气工程学院，武汉 430033）

随着全球变暖，北极地区冰化加剧。本世纪中叶北冰洋夏季预计将出现全域通航的状态，北极航运价值将日益凸显。提前开展极区导航技术和装备研究十分必要。在极区进行航运、探索等活动中，惯性导航设备作为一种重要的自主导航设备，其极区工作性能的检验是一个重要和复杂的问题。特别对于地理位置相对远离极区的国家，在极区进行大规模海上航行试验周期长、成本高，实际实施十分困难[1]，因此需要研究基于中低纬度试验航次的被试惯导与参考基准的数据，采用一定方法推算评估被试惯导在极区采取相似运行轨迹和机动状态的精度性能，这项技术称为“惯性导航系统极区性能的中低纬度模拟测试技术”，本文简称为“极区中低纬度模拟测试技术”。

对于这种利用中低纬度载体运动轨迹和IMU 原始输出转移至极区进行极区算法验证的技术，已有学者进行了相关研究：文献[2][3]讨论了虚拟极点(极区)的方法，本质是重构地球经纬网将当地自定义为虚拟极区，实现在当地中低纬度下对惯导极区算法进行验证的目的；这一方法存在的问题是无法模拟反映出极区真实的重力矢量与地球自转矢量等测量条件；此后的研究主要是在轨迹转移基础上同时对IMU 数据进行转换，重新生成极区的模拟IMU 数据，模拟的IMU数据除可用于本惯导极区测试，还可用于地形匹配、重力匹配、组合导航等其他方面。文献[4]对地球系(地心地固坐标系)坐标轴进行旋转以构建轨迹，并讨论了IMU 的转换公式，仿真验证能通过中低纬度测试航行验证极区算法的有效性；文献[5]则对模拟极区技术做了一定的分析；文献[6]第4 部分中给出了中低纬度到极区轨迹转移的部分IMU 转换公式，并基于此完成了横向编排的惯性导航算法在极区的性能验证。上述对轨迹转移方法和IMU 转换算法的研究，仅能进行极区算法验证，还不足以支持在中低纬度对惯导系统开展模拟测试。关于极区模拟测试理论，文献[7][8]具体给出了椭球模型下的基准转换及IMU 转换公式，完善了模拟测试系统的结构和理论，数字试验证明在基准误差不计的条件下模拟惯导性能与极区实地惯导性能相当。文献[9]则以旋转调制惯导为对象，也研究了模拟测试中IMU 数据转移问题，并认为高纬度模拟数据可以反映旋转调制惯导的特性，数据精度也能够符合误差分析的要求。

不同于极区算法的有效性验证，对于实际的高精度惯导性能测试，参考基准误差是影响模拟测试精度评估的关键因素之一。但基准误差对模拟测试系统的影响，由于分析困难，前人文献中大都予以忽略或仅仅停留在定性估计阶段。为解决这一问题，本文从惯导系统极区性能中低纬模拟测试的定量误差分析角度，分析推导了惯导各主要导航变量模拟测试中受中低纬基准误差影响的程度，并最终推导出地球球体模型下载体中低纬地表运动下模拟极区IMU 输出转换修正量误差的完整公式，为进一步的惯导极区模拟测试系统搭建与评估等工作奠定了重要的理论基础。

1 极区中低纬模拟测试方法

由于本问题的理论分析较复杂，为简化分析，本文取地球模型为球体模型，载体应用条件限于地表导航。并确定中低纬度至极区高纬度的轨迹转移策略为转移前后载体的速度、姿态、轨迹形状相对横向坐标系保持不变。

假设配备导航基准参考系统的载体在中低纬度搭载被试捷联惯导在横向赤道附近运行，被试惯导输出IMU 数据分别为载体(b 系)上导航参考基准给出的速度、姿态在当地地理坐标系(g 系)下分别表示为基准轨迹(位置)为p，即纬度φ、经度λ。横向坐标系的定义可根据需要人为指定（在地理赤道上选取适当的位置定义横向极点，使待转移轨迹处于横向赤道附近），基本变量计算及横向惯导编排不再赘述，详见文献[10][11]等。

依据转换公式，将基准导航参数投影至当地横向地理坐标系(t 系)表示为

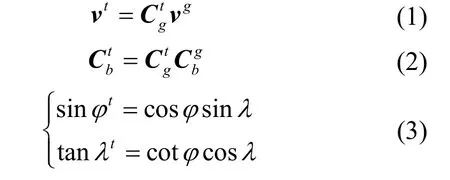
其中

其中Λ 表示轨迹沿横向纬线移动的角距离，即经度跨度，本文称为“轨迹转移角”。轨迹转移如图1 所示。

图1 轨迹转移示意图Fig.1 Demonstration of trajectory transformation

图1 中仅绘出了横向纬线圈。N 表示传统北极点，处于横向赤道上。至此取得了模拟基准的各导航参数。

根据惯导解算方程中的比力方程和姿态矩阵微分方程：

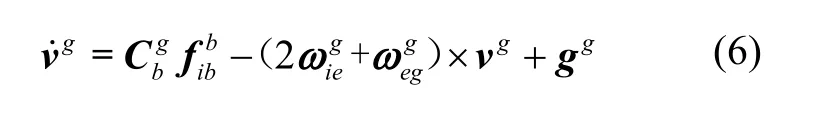
其中“×”表示变量的反对称矩阵(下文同)。以“tm”表示模拟极区地区横向地理坐标系，“bm”表示模拟极区地区载体坐标系。将式(6)(7)中g 分别置换为t 和tm(b系也对应取b 或bm)，表示实测地区和模拟极区地区均应成立的IMU 解算方程，然后根据转移前后横向地理坐标系下速度、姿态不变的转移原则列写关系式：

可以得到，模拟地区运行的惯导IMU 数据与实测惯导IMU 数据应当满足式(9)(10)。

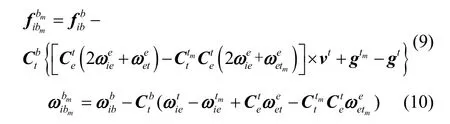
极区中低纬模拟测试工作就是将极区模拟基准的导航参数与被试惯导极区模拟解算数据对比，以评估被试惯导的极区工作性能。

图2 展示了该模拟测试系统的关键技术环节。实测基准数据经历了“g-t-tm”的坐标转换形成极区模拟基准数据，实测IMU 数据经转换修正后直接以tm系为导航坐标系进行解算，其解算结果直接与处在tm系的模拟基准进行比较、分析和评估。

图2 惯导极区模拟测试原理流程图Fig. 2 Flow chart of INS polar simulation test system

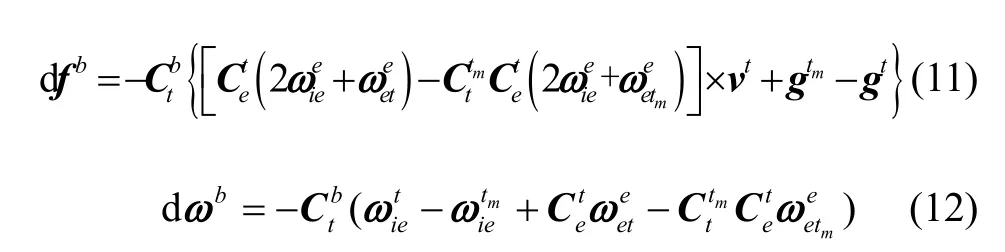
dfb、dωb分别表示IMU 中加速度计和陀螺仪极区模拟输出的转换修正量，实测惯导IMU 数据加上IMU 转换修正量即得到极区模拟的IMU 数据。由于IMU 转换修正量的计算需使用基准测量的导航参数，因此基准误差将造成IMU 转换修正量的计算误差，进而导致模拟的IMU 数据出现误差，此误差是极区中低纬模拟测试方法最主要的误差之一，必须加以分析。

2 基准误差分析与建模

如上所述，基准误差是极区中低纬模拟测试中重要的误差源，本节从分析基准数据来源出发，构建合理的基准误差模型，进行基准误差的表示。

2.1 基准参数获取分析

设中低纬度导航基准参考设备输出位置、速度、姿态等导航参数为当地地理坐标系下的值，暂且仅考虑地球表面导航的情况。

考虑测试实际情况，一般由卫星导航设备(如GPS、BDS)独立给出位置基准；航姿基准可依赖高精度星敏感器的观测，精度优于角分级；速度基准可由卫星导航系统或者高精度计程仪给出。也可选择最常用的高精度惯导与卫导等组合导航系统，提供相应的位置、速度和航姿等导航参数基准，此时基准航向、速度误差与基准定位误差不独立。

鉴于基准数据来源的复杂性，考虑不同基准导航参数误差之间的关系非常困难，由不同设备来源、不同组合方式乃至不同的滤波模型都将产生不同的结果。为便于分析，本文不具体研究上述基准参数产生方式，将基准的各导航参数误差暂时视为相互独立，着重进行模拟测试过程中的误差传播分析。

2.2 基准误差的表示

位置基准输出值一般为地理经纬度，将位置基准误差模型表示为：

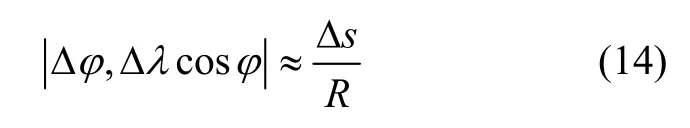
R 表示地球球体模型半径。速度误差模型在地理坐标系和横向地理坐标系中可分别表示为：

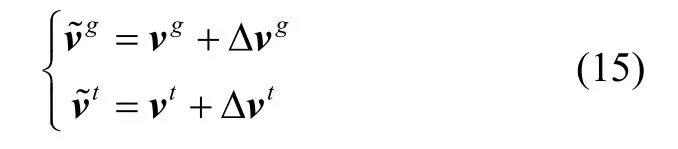
其转换关系为式(1)，由于仅考虑地表导航，速度矢量中包含东向分量和北向分量：

基准误差通常量级很小，根据罗德里格斯（Rodrigues）旋转公式，取一阶近似得：

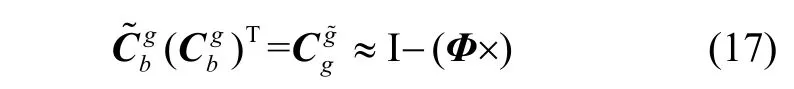
3 基准误差对IMU 极区模拟转换修正量各变量的影响分析

基本分析思路如下：首先分析位置、速度、航姿等建立各导航参数基准误差模型，分别代入IMU 转换修正量计算公式(11)(12)中，最终推导分离出IMU 转换修正量误差的具体表达式。

3.1 位置基准误差的影响

将位置误差模型代入到转换公式相关的各矩阵变量中，研究位置矩阵以及有关的地理坐标系变换矩阵在定位误差影响下的具体误差表达式，进而分析定位误差影响效果。

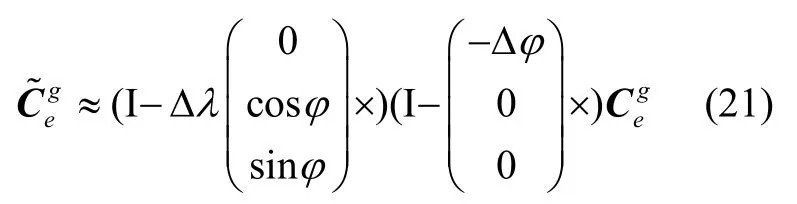
展开并忽略其中二阶小量，利用小角度转动的可交换性得：

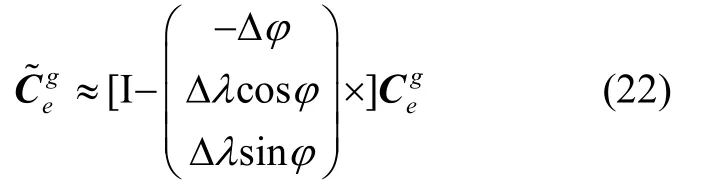
3.1.2 实测地区到极区模拟地区横向地理坐标系转移矩阵

由计算公式：

可得表达式：

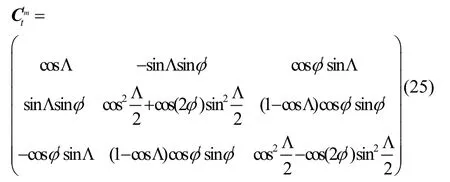
基准的横北向位置误差(横纬度误差)将对其计算产生影响，易知其误差量级与Δφt相当。

3.1.3 基准位置误差影响综合分析

基准定位信息来源通常是卫星导航系统，定位误差量级为米级或亚米级，其在位置矩阵、地理坐标系转移矩阵等计算中的影响均在Δp/ R 量级，为10-7～10-6rad，在0.1 角秒左右，误差甚微。目前姿态测量精度尚难达到角秒级，速度测量精度在0.1 m/s附近，代入IMU 转换方程中，发现姿态、速度误差影响远大于位置误差的影响。综合分析，以目前速度、姿态测量水平和测试要求，基准定位误差对位置矩阵、地理坐标系转移矩阵计算的影响完全可忽略不计。

步骤1：初始化候选断点集，令CUT={Caj︱j=1,2,…,m}，其中Caj为条件属性aj的候选断点集。

3.2 基准速度误差对变量 、 计算的影响

其中

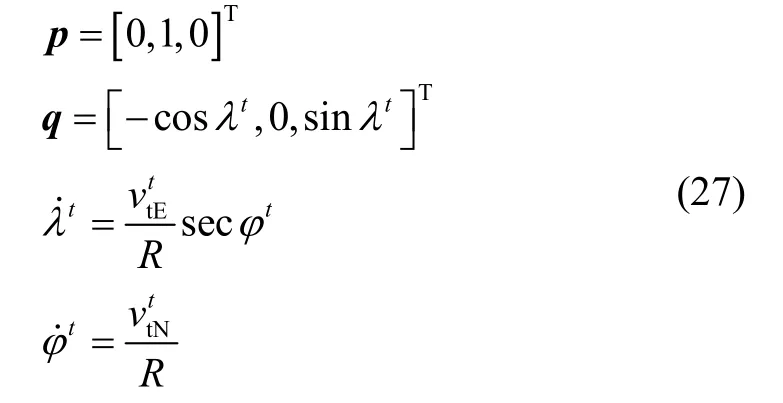
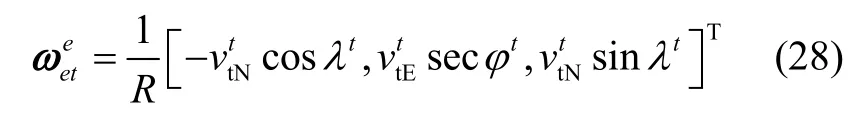
同样地，速度误差对此变量造成的影响远大于定位误差对其的影响，因此：

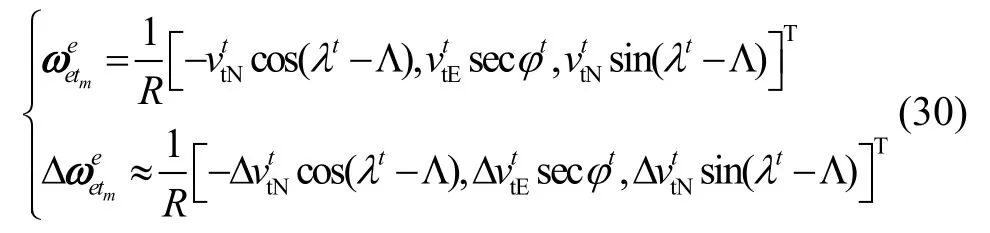
3.3 基准姿态误差对变量计算的影响

横向地理坐标系下的姿态矩阵误差模型可表示为：

推导可得向量Φt与Φ 的关系：

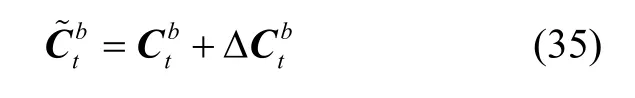
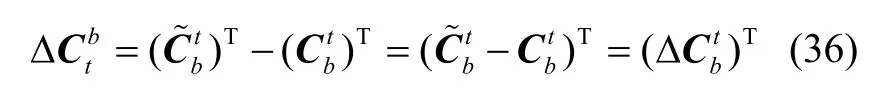
3.4 重力变量的计算和误差处理方式

对重力变量gt，本文采用一般重力的达朗贝尔方程对其误差进行计算分析。由于重力异常和垂线偏差是影响高精度惯导系统精度的重要因素，可通过实测数据库和相关技术，实时补偿垂线偏差、重力异常等因素，才能进一步提升惯导精度水平。本文暂不对此进行深入讨论。此外，基准位置误差显然可造成的一般重力的计算误差，由于其影响甚微，可忽略。达朗贝尔方程如下，其中g0=9.780325 m/s2：

4 IMU 转换修正量误差模型

综合基准误差对变量计算的影响程度，根据式(11)(12)，列写加速度计、陀螺仪转换修正量计算模型如下：

将存在误差的计算量表示为理论值和偏差值相加，展开表达式后分别与式(11)(12)相减，忽略二阶以上小量化简可得IMU 转换修正量误差的符号表达式如式(39)(40)所示。

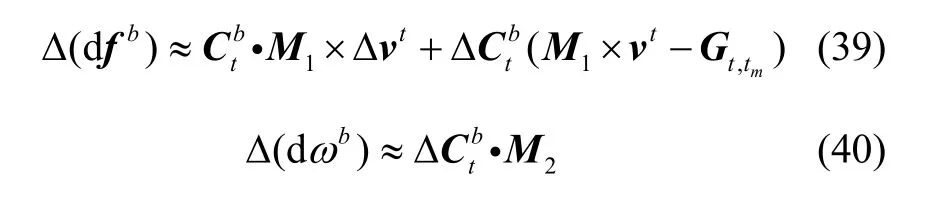
可注意到表达式中模拟IMU 陀螺仪输出转换修正量误差仅与基准姿态误差有关。其中 gt、gtm分别表示测试地区和模拟地区重力加速度的大小：

经尝试，采用传统地理坐标系下的基准误差作为源变量表示IMU 转换修正量误差，公式十分冗长，考虑到公式表达的相对简洁性，采用横向速度误差与姿态失准角误差作为源误差变量，列写IMU 转换修正量误差的表达式结构如下：

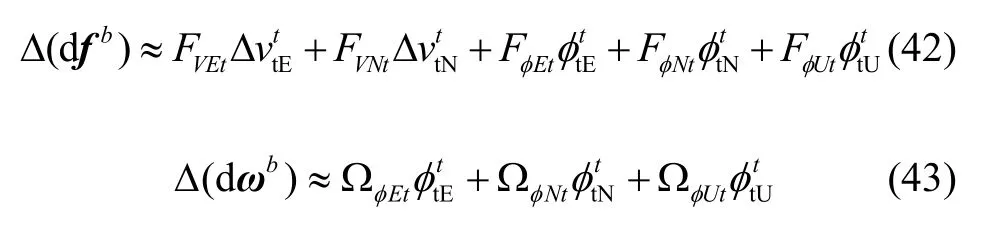
此模型可体现误差源的各个分量对IMU 转换修正量的影响，通过计算其中的各个系数便于分析不同误差源对IMU 转换修正量影响的方式和量级。借助软件Wolfram®Mathematica 7 进行符号运算推导，可得表达式中各个系数，见表1。

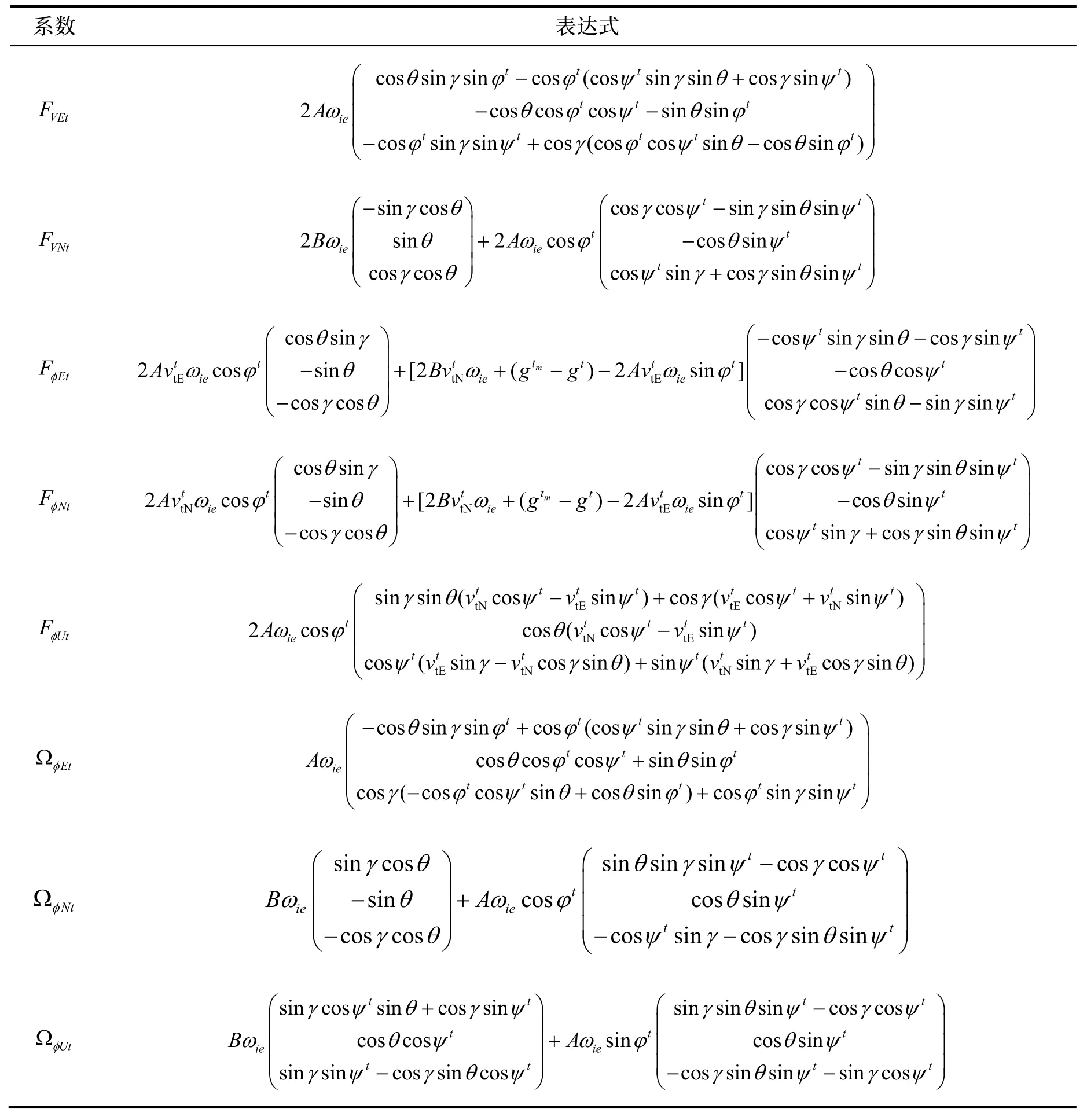
表1 IMU 转换修正量误差公式中的系数Tab.1 Coefficient in error formula of IMU conversion correction variables

式中 ωie为地球自转角速度、ψt为横航向角，A、B 分别代表：

5 仿真试验

为检验IMU 转换修正量误差公式推导的正确性，利用参考基准的跑车测试数据[12]进行IMU 极区模拟转换修正量误差的计算。

由实测轨迹中心经纬度(约114.47 °E、30.452 °N)，选取轨迹中央经线114.47 °E 为横向赤道以构建横向坐标系，设置轨迹转移角Λ=59.548 °，使模拟测试区域在北极点附近。

采用数据中基准系统输出的“avp”全导航参数，设置此基准存在常值系统误差：纵摇误差-1′，横摇误差1′，航向误差3′，东向、北向速度误差均为0.1 m/s，代入公式(42)(43)和表1 中，计算结果（图3）显示，IMU 中陀螺仪与加速度计转换修正量误差各分量量级最大约为0.01 °/h(6×10-8rad/s)与2 μg(2×10-5m/s2)，初步说明这一精度水平的基准在较高精度的惯导极区模拟测试中造成的转换误差是不可忽略的。

该计算结果与理论值(将基准参数与叠加误差的基准参数直接用于变量计算，代入式(11)(12)并对应相减)比较，结果见图4，其中上图为误差模型计算的陀螺仪转换修正量的偏差，最大不足10-5°/h，下图为误差模型计算的加速度计转换修正量偏差，最大不足2×10-3μg，与图3 中IMU 转换修正量的量级相比较均在1‰以下，验证了本文所推导的误差模型的正确性。

图3 IMU 转换修正量误差解算Fig.3 Error of IMU conversion correction variables

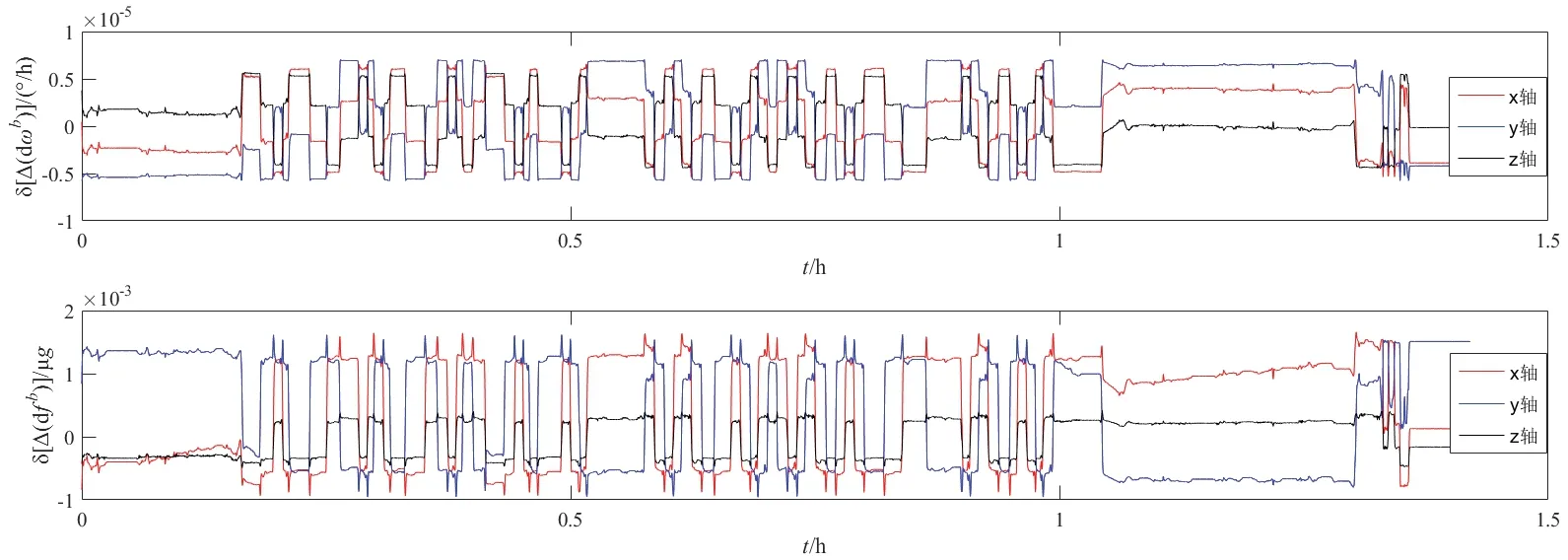
图4 模型计算IMU 转换修正量误差的偏差Fig. 4 Bias of the error of IMU conversion correction variables calculated by model

6 结 论

针对惯性导航极区中低纬模拟测试系统中IMU转换过程产生误差的问题，本文开展了IMU 转换修正量误差的定量分析工作，推导了参考基准误差导致的极区模拟转换修正量误差的表达式（见式(39)(40)）及其完整展开式（见式(42)(43)和表1），经分析，有如下主要结论：

(1)基准定位误差在IMU 输出模拟转换修正过程中的误差影响较小，可忽略不计；(2)参考基准的姿态误差是造成IMU 陀螺模拟转换修正量误差的最主要原因（见式(40)）；(3)参考基准的速度、姿态误差均可造成IMU 加速度计模拟转换修正量误差(见式(39))；(4)中低纬实测地区与模拟极区地区间的重力差异将通过参考基准水平姿态误差的传递修正计算造成IMU 模拟加速度计输出误差（见表1），重力异常、垂线偏差等因素影响有待进一步研究。(5)本文所得公式可运用于船载惯导系统以及机载惯导系统的极区水平机动模拟测试，包含高度通道的误差影响公式还需进一步推导。

本文开展的惯导极区中低纬模拟测试中的IMU转换修正量误差的定量研究工作，为惯导极区中低纬模拟测试技术的精度分析和测试设计提供了理论分析方法，为未来惯导极区中低纬模拟测试的工程化实施奠定了必要的理论基础。由于推导获得的IMU 转换修正量误差系数仍较为复杂，公式的实际工程应用以及IMU 转换修正量误差对极区模拟惯导系统影响的深层机理仍需进一步研究。