逆向教学设计:打开理解学习的一扇窗
林燕娟
【摘 要】逆向教学设计以终为始,从学习结果出发,以合适的评估依据即时调整设计,并通过丰富的体验和学习活动达成目标。逆向设计从关注教材走向关注学科关键能力,以基本问题打开理解之门,以丰富的评估证据促进学生的理解。
【关键词】逆向教学设计 数学理解 设计路径
教学设计是教师依据自己对教材理解的一种演绎,是课堂教学的蓝图。在传统教学设计中,教师通常聚焦于输入端,思考教什么、怎么教,忽略了学生的“学”。因此,教师需要切换视角,寻找新的设计思路,美国教育家格兰特·威金斯和杰伊·麦克泰提出的以理解为先的逆向教学设计为我们的教学设计打开了一扇窗。
一、本质解读:逆向教学设计和数学理解
(一)逆向教学设计的内涵
逆向教学设计,从字面含义来说就是从学习结果开始逆向思考设计,即“以终为始”,其切入点在于学习结果,落脚点在于学生的理解,以促进学生深层理解为宗旨,以“关键问题”为抓手,通过丰富的学习体验和活动来实现学习目标。
(二)对数学理解的再认识
理解就是一种对事物本质的认识,即要知其然又要知其所以然。数学理解就是能有效地建构认知结构和知识意义,能够智慧有效地使用知识和技能。
1.数学理解的目标指向:意义与联系
所谓数学理解指学生不仅要学习数学知识,知道其中蕴含的意义,更要对这类知识之间的联系有清晰的认知,从而达到更加丰富、更加精细的理解之态。
2.数学理解的核心要义:灵活迁移
帕金斯说过,理解是“能够灵活地运用知识进行思考和行动的能力”,理解的最终目的就是让学生获得对知识的有效迁移能力,这里所说的知识既包含陈述性知识,也包含程序性知识,还包含学习活动中所经历的情感体验、经验生长、心理感受等具有默会特征的过程性知识。
二、有效追寻:基于理解的逆向教学设计的路径
逆向教学设计有三个阶段:一是明确预期的学习结果是什么,需要持久地、深入地理解的知识内容有哪些;二是建立达到预期学习目标的证据,证明是否掌握了相关的内容;三是设计相关的体验学习活动,达成预期的学习目标。基于理解的视角,数学教学究竟应该如何进行逆向教学设计呢?下面以苏教版数学五年级上册“小数乘法”一课为例进行设计探索。
(一)明确预期的学习结果
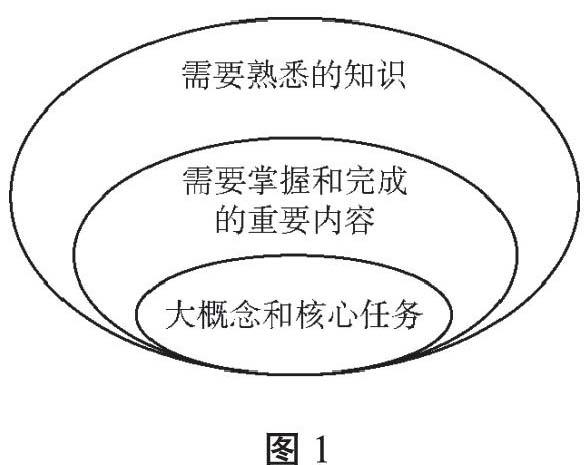
预期目标的确定首先要对单元的内容设置进行取舍和整合,明确学习内容的优先次序,促进学生理解。格兰特·威金斯设计的课程内容优先次序框架图(见图1)为我们选择课程内容提供了范本。
小数乘整数这一內容需要学生熟悉的知识是“整数乘法的计算方法和小数的意义”,是学生需要一般了解的内容;需要学生掌握和完成的重要内容是“算法的探索、算理的理解及其运用”,这是学生务必知道并能做到的重要的知识和技能;需要学生持久性理解的内容是“小数乘整数的意义和算法”,这是核心任务,是学生持久性理解的内容,能帮助学生迁移应用于新的环境。分析这一课的课程内容,笔者将“小数乘整数”逆向教学设计预期目标进行了细化。
确定目标:探索小数乘整数的计算方法,贯通算理的多种表征,实现概念性理解,感受转化和数形结合思想;熟练掌握计算方法,形成技能,有效迁移到小数乘小数。
学生要了解的基本问题:小数乘整数的算法和算理是什么;为什么乘数中一共有几位小数积就有几位小数。
学生将理解:小数乘整数的算法与算理;小数乘整数与整数乘法的算法沟通。
学生将会知道:小数乘整数算式表示的意义;小数乘整数的算理表征及之间的联系;小数乘整数的算法。
学生将能够做到:将整数乘法的算法迁移到小数乘整数的计算;将小数乘整数的算理与算法建立联系,确定小数乘整数时积的小数点位置,从而正确计算。
学习小数乘整数的基本要义在于引导学生学会从“小数的意义、数形结合、计数单位的几何倍增”多种角度理解算理和算法,从而理解所建构的大概念,优化算法形成运算技能,提升运算能力,这也是培养学生数学学科关键能力的诉求。
(二)确定合适的评估依据
基于预期的学习目标,教师要作出相应的评价,像评估员一样思考:什么样的证据可以确定学生的理解程度,怎样做才能知道学生已经达到了预期目标。
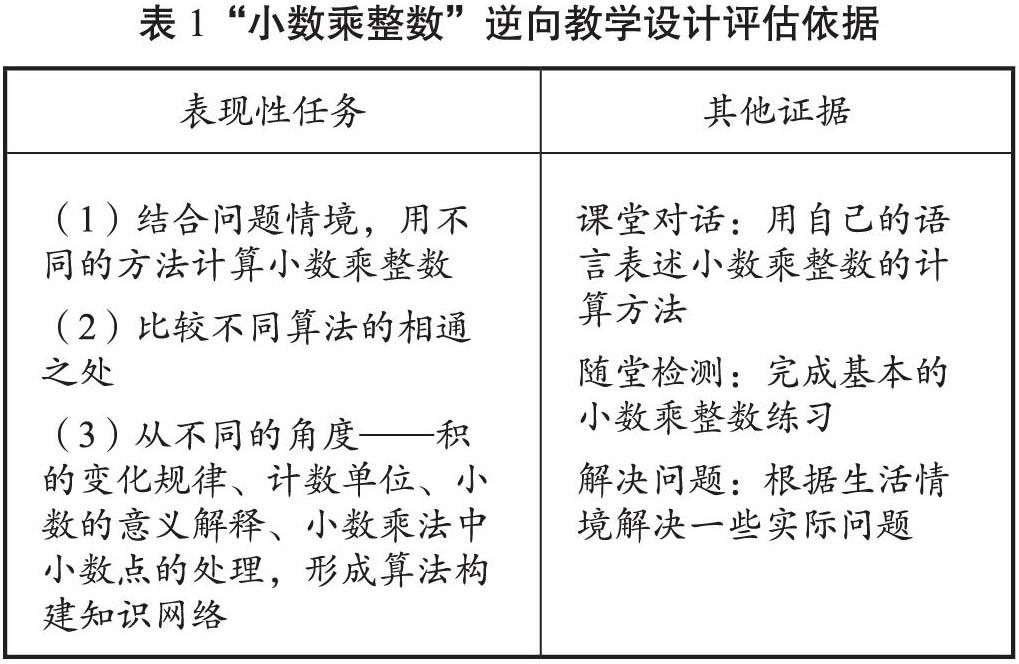
例如,在学习“小数乘整数”时学生是否达到了预期的学习目标,即算理与算法的有效融合,以及会运用竖式计算方法解决数学问题。除了用对话、观察等证据检测知识技能的理解,还可以围绕基本问题设计表现性任务,来评判学生能否灵活运用掌握的知识和技能进行思考,展现对知识的理解。(见表1)
(三)设计相关的学习体验和教学活动
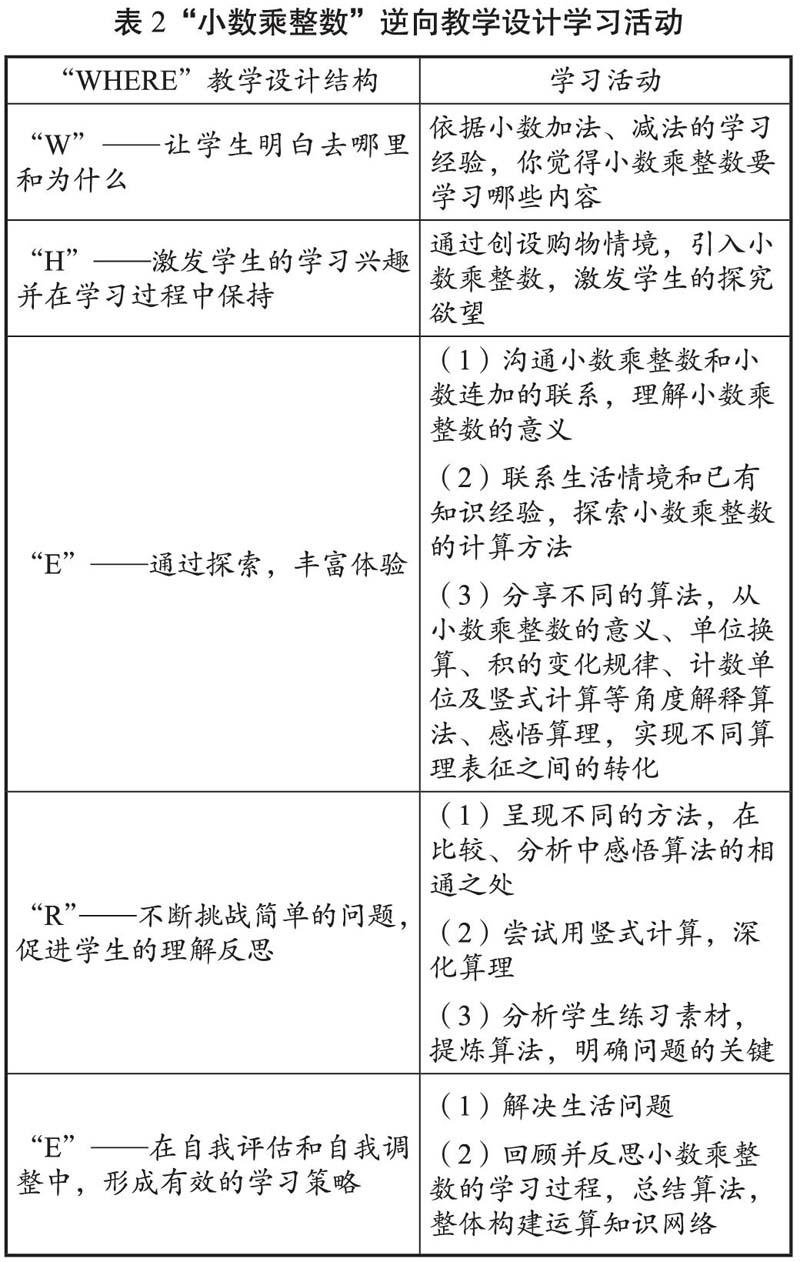
一个好的学习活动设计,既要有吸引力,又要有实效性,要能促进学生在解决问题的过程中提高知识转移和应用的能力。如何在教学设计中体现这些特点,“WHERE”设计元素为我们提供了一条有效的教学设计路径。(见表2)
小数乘整数的学习活动设计特别关注了知识意义的构建,借助“乘法的意义”“积的变化规律”和“计数单位”这些学生已有的知识经验表征其算理,通过直观表征与抽象表征之间的转化,获得对数学概念意义的理解。当学生能够将概念从一种表征转化为另一种表征形式时,也就真正理解了小数乘整数计算的算理和算法。
三、基于理解的逆向教学设计的反思
“小数乘整数”一课教学设计的探索与实践,让我们对逆向教学设计也有了一些认识和体悟。
(一)从关注教材走向学科关键能力
逆向教学设计的依据是课程标准而非教材,教材只是教学内容的一个载体,教师需要跳出教材,灵活用好教材,思考知识之间的关联,发掘知识背后的意义、价值以及蕴含的数学思想方法。“小数乘整数”的教学中围绕大概念和核心问题确定内容主旨,围绕知识迁移和应用的表现性任务评估来进行教学设计,这种“目标导向”“评估导向”的设计使教学活动指向更加明确,教师有据可循。教师在教学中以有意义的生活情境和有思维梯度的问题链,帮助学生深入探究,在问题解决过程中培养学生的逻辑推理、表征和数学运算能力。
(二)以基本问题打开理解之门
“基本问题”是理解的关键,以基本问题串联学习内容,发掘学习内容中隐含的思维和逻辑,可以促进学生迁移能力的形成,真正实现学生的深度理解。如在教学“小数乘整数”时可以问“小数乘整数的计算方法是什么,为什么可以这样算?”通过来自课程内容的基本问题的设定,吸引学生进行计算方法的探究、发现,理解方法的本质。在这个学习过程中,学生有效地迁移了整数乘法的学习经验,用积不变的规律和小数的意义解释算理,并为后续学习小数乘小数算理的理解和算法传递了一种强烈的信号,有利于学生对计算法则建立系统认知。
(三)丰富评估证据促进理解
理解是一个不断生长、不断深化、具有多元表现、多元内涵的复杂过程与现象。因此,对学生是否真正理解的评价不能仅仅局限于对学生是否获得了数学事实和程序的检测,它应具有全方位的证据和对证据的深入分析。例如,通过观察学生的活动与行为,评估学生对数学概念的理解和问题解决等;通过课堂交流讨论,了解学生推理迁移等信息,依据获得的信息及时调整教学策略,以评价的多元性顺应理解的多元性。
总之,基于理解的逆向数学教学设计,有效地提高了数学教学设计的针对性,实现数学知识深入持久的理解,对教师从新的视角进行教学设计具有重要的指导意义和价值。

