基于粒计算和使用次数的大数据价值计算方法

马文胜，侯锡林，王宏波，柳 森

（1.辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051；2.辽宁科技大学 工商管理学院，辽宁 鞍山 114051）

20世纪80年代，美国未来学家Alvin Toffler在《第三次浪潮》中第一次使用“大数据”一词，并指出大数据是第三次浪潮的华彩乐章［1］。从此大数据开启了一次重大的时代转型，大数据是改变市场、组织机构以及政府与公民关系的方法；大数据还是人们获得新的认知、创造新的价值的源泉［2］。

随着计算机技术、网络通信技术、智能终端设备以及各类信息系统在各领域的应用，大量的数据在开放多源的渠道中产生，逐渐汇聚成一个巨大的、精准映射并持续记录物质世界和精神世界运动状态和状态变化的“大数据”空间［3］。在这个大数据空间中，大数据蕴藏着巨大的科学研究价值、公共管理与服务价值、商业价值以及支持科学决策的价值［4-5］。一方面，对大数据的掌握程度可以转化为经济价值的来源；另一方面，大数据已经撼动了世界的方方面面，从商业、科技到医疗、政府、教育、经济、人文以及社会的其他各个领域［2］。

在众多领域中，人们也逐渐的发现，大数据使用的越多，其体现出来的各种价值就越大。只有使用，大数据才能体现出价值；反之，如果没有使用，大数据就体现不出任何价值。因为价值的本质就是数量性存在，所以大数据价值也应定量计算。

目前的研究还都没有给出大数据使用数量与其价值之间的计算关系。本文定义了一个体现大数据使用情况的粒函数，并证明了该函数的一些重要特殊性质。在此函数的基础上建立了一种新的、可计算出价值数值的大数据价值模型。给出了这种模型计算出的大数据价值范围，以及简洁实用计算方法和应用程序。该算法依据Garter字典序，来检测各个粒子集。对空函数值及同函数值子集给与处理，极大地减少了计算工作量。并通过实际使用也对算法的简洁实用性及该模型的粒度单调性、数据量单调性作了实验验证。

1 大数据研究

1.1 大数据价值研究

大数据已经被看作是战略性基础资源，是获得竞争优势的关键因素［6］。所以研究大数据本身的价值，其作用是不言而喻的。目前学者们对于大数据价值计算及价值评估的研究，在理论上给出了很多各不相同的研究方法和方向。

（1）按照一种定价模型方法对大数据价值进行研究。资产定价模型在上世纪60年代就已提出，近年来被使用到大数据价值研究。诺贝尔奖得主Fama等研究出较为完善的资产定价模型的理论体系。Fama通过确定跨期资本资产定价模型状态变量的数量研究以及价格对该模型的影响，得出跨期资本资产定价模型不同于资本资产定价模型［7］，并进行了溢价条件下的资本资产定价模型研究［8-9］。Hansen针对理性预期假设制定和估算了价格动态线性计量经济模型［10］。Shiller通过简单有效的市场假设、总变差的推导和回归模型的检验，建立了普遍适用的有效市场价格模型［11］。近年来，国内学者也在大数据定价模型的相关理论和实证方面进行了探讨，例如，Chen等根据传统拍卖模型，提出了在不同条件下的两种拍卖模型对大数据价值予以定价，并分析了相应方法的收益期望［12］。

（2）按照一种数据资产对大数据价值进行研究。“大数据之父”Mayer-Schönberger认为，大数据作为一种无形资产，是企业重要的战略资源，数据资产列入资产负债表，只是时间问题［2］。在对数据资产影响因素分析的基础上，引入了收益现值法、市场价值法、重置成本法、博弈方法、人工智能方法对数据资产定价方法进行研究。目前，数据已作为一种新型生产要素写入《中共中央国务院关于构建更加完善的要素市场化配置体制机制的意见》，强调要加快培育数据要素市场。

（3）按一种价值评估方法对大数据价值进行研究。侯锡林指出“对大数据的价值进行科学的评估和计算，创建大数据的价值模型，无论在理论上还是在实践中，都是亟待解决的最重要问题”［13］。David对数据资产价值评估采用收益法，并验证了评估结果［14］。Chiu等将数据资产视为无形资产，利用层次分析法进行价值评估，将大数据技术的特性、成本、产品市场、技术市场四方面因素量化进而评估数据资产价值［15］。Lin等基于大数据价值来源分析，从价值驱动方面构建价值评估模型，并将收集到的6个行业数据使用于该模型，以验证模型的适用性并提出模型使用建议［16］。Jorge以“3As数据质量使用模型”评估数据质量水平，该模型选用情景、运营、时间适当性三方面特征作为质量指标分析［17］。Niyato等基于数据科学视角与数据市场模型的分析研究大数据价值，提出最优的定价方案并利用相关案例进行适用性的证明，认为该模型可以实现数据提供者的利润最大化［18］。

当然，还有很多国内外的研究者为研究大数据的价值，采用了很多各不相同的方法。但是目前的研究都是对大数据价值的经济量化计算进行讨论，是对大数据作为一种经济产物的描述，而不是计算出大数据本身的价值，所以这些传统的方法也就都无法满足人们对大数据自身价值量化的期望。

1.2 大数据与粒计算

大数据又称为巨量数据、海量数据、大资料等，是指无法在一定时间范围内通过人工或计算机进行捕捉、管理和处理的数据集合，是需要新处理模式才能具有更强的决策力、洞察发现力和流程优化能力的海量、高增长率和多样化的信息资产［19］。由于大数据不能用传统的方法进行处理，所以大数据的价值计算也必须使用非传统的方法。Chen等将“粒计算”列为驾驭大数据的第一方法［20］。

粒计算的基本思想是把初始形式的数据划分为不同的粒度进行处理。用粒度合适的“粒”作为处理对象，从而在保证求得满意解的前提下，提高解决问题的效率［21］。

对大数据进行粒化的具体方法中，模糊信息粒化法通过模糊化和粒化组合划分得出模糊规则、语言变量、模糊图［22］；粗糙集近似法通过研究简单和层次粒化与近似，考察粒结构划分和粗糙集近似［23］和商空间法，将等价类描述的粒度与商集概念统一起来，研究不同粒度划分下相互转换、相互依存关系［24］。本文亦将基于粒度“划分”对大数据进行粒化，来计算大数据的价值。

2 粒空间和使用关系

定义3［25］设A为大数据D的对粒度G的使用关系，G⊆G，则G的函数φ(G)为

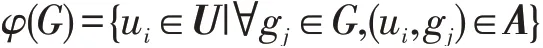
并规定φ(∅)=U。

3 大数据价值

3.1 使用关系与大数据价值

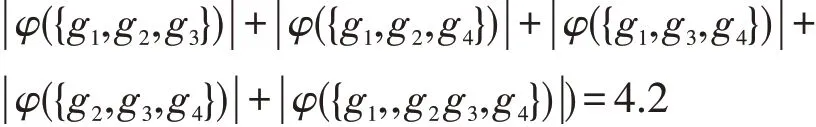
3.2 大数据价值的范围

例5 设D是大数据，G={g1,g2,…,gn}是D的一个粒空间，U={u1,u2,…,um}是选取的一些项目，A={(ui,gj)|i≡j(mod n),1≤i≤m,1≤j≤n}，即当且仅当i与j对n同余时，(ui,gj)属于A。例如n=4，当且仅当i与j对4同余时，(ui,gj)属于A。若m=11，则A如表2所示。

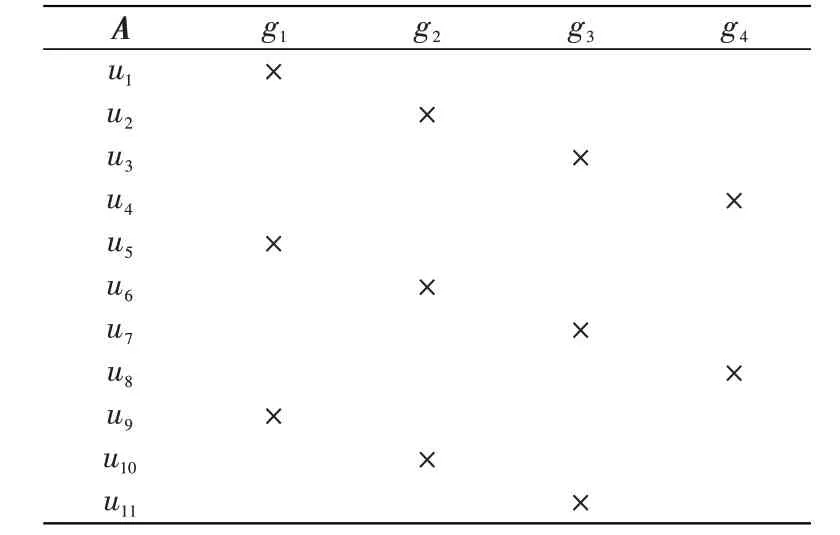
表2 一种特殊的使用关系Tab.2 Aspecial usage relationship

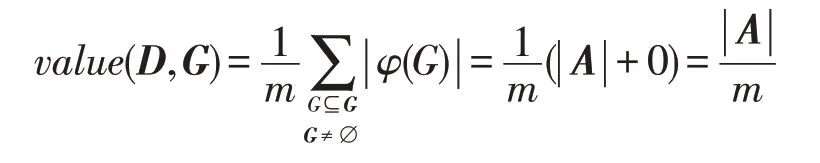
3.3 粒度单调性与数据量单调性

3.3.1 粒度单调性 大数据的粒度变细，数据的使用情况就看得更清楚，于是价值体现的就应更大些。这是粒度单调性。现在证明价值公式可体现这一点。

定义5 设D是大数据，G={g1,g2,…,gn}及H={h1,h2,…,hn′}是D的两个粒度，若每个gj都是某些hi的并集，而且若大数据D对粒度G的关系是A，大数据D对粒度H的关系是B，而gj=hj1∪…∪hjk(1≤j≤n)，则A,B满足(ui,gj)∈A⇔(ui,hj1)∈B∨…∨(ui,hjk)∈B(1≤i≤m,1≤j≤n)，即满足ui使用了粒gj，当且仅当ui使用了粒hj1或使用了粒hj2……或使用了粒hjk，则称粒度H细于粒度G，记作H≤G。

例6 设D是大数据，U={u1,u2,u3,u4,u5}是项目，G={g1,g2,g3,g4}是一个粒度，D对粒度G的关系A如表1所示，H={h1,h2,h3,h4,h5,h6,h7}是另一个粒度，满足g1=h1∪h2，g2=h3，g3=h4∪h5∪h6，g4=h7，而D对粒度H的关系B如表3所示。

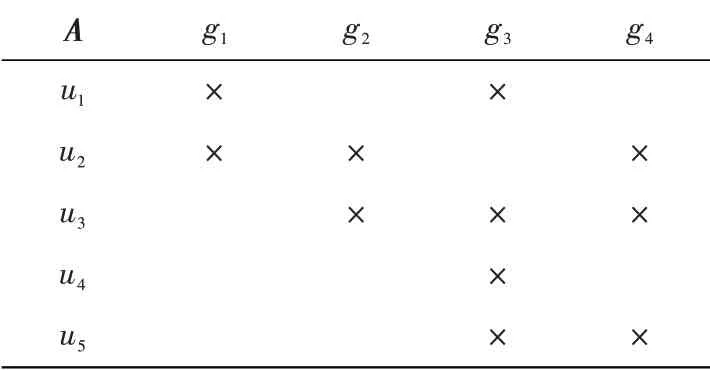
表1 一个大数据的使用关系Tab.1 Usage relationship of one big data

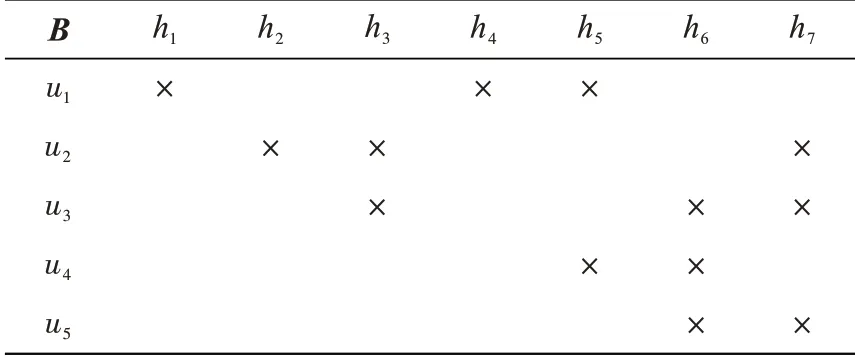
表3 细粒度的使用关系Tab.3 Usage relationship of refined granularity

颠倒⋂和∪的次序，若G={gi1,…,gip}，则上式相当于对每个git(1≤t≤p)都取一个是其子集的

3.4 数据价值的算法

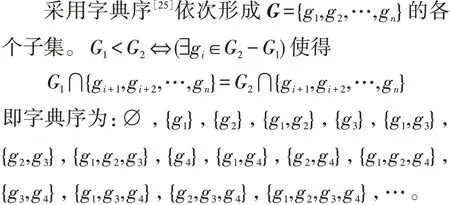
算法在形成各子集的过程中，φ(G)=∅的子集G不存入，φ(G)相同的G只存入一个，采用计数形式记录子集个数，极大减少了计算工作。

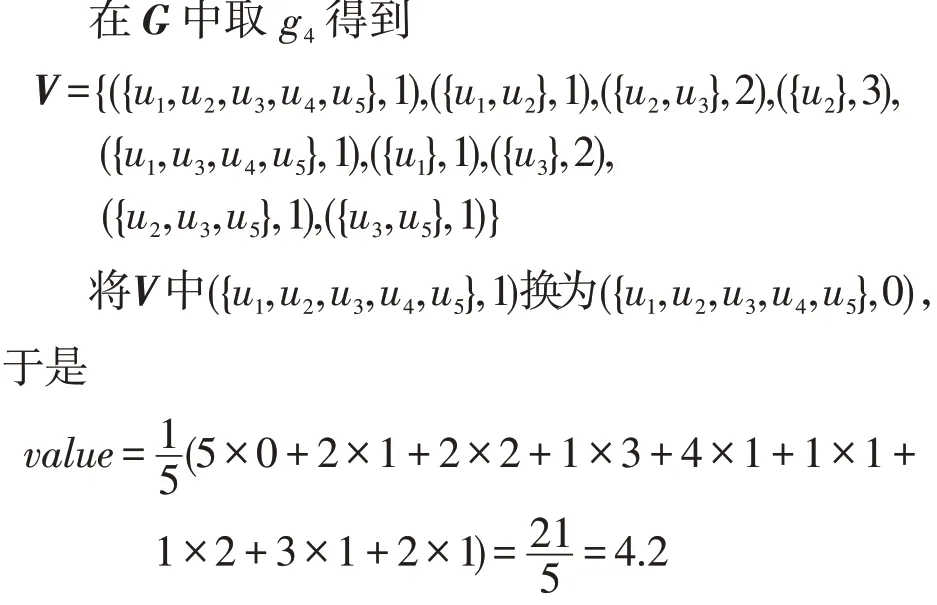
定理4 算法1是正确的。

证 首先规定一种“计数集合”。元素a,b,b,c,c,c,c形成的集合是{a,b,c}。规定形成的“计数集合”是{(a,1),(b,2),(c,4)}。

另外不失一般性假定步骤（3）从G中取g的次序就是g1,g2,…,gn。

下面用归纳法证明到步骤（15）时，V中的内容将是G={g1,g2,…,gn}的所有子集V求出的φ(V)形成的“计数集合”。

初始：步骤（1）后，V中的内容是{(φ(∅),1)}，是空集求出的φ(V)形成的计数集合。

归纳：设步骤（3）取gt后，到步骤（13）时，V及V′中的内容是{g1,…,gt}的所有子集V求出的φ(V)形成的计数集合。证明步骤（3）取gt+1后，到步骤（13）时，V′中的内容（从而V中的新内容），将是{g1,…,gt,gt+1}的所有子集V′求出φ(V′)的形成的计数集合。在这个过程中用V保存{g1,…,gt}的所有子集V求出的φ(V)形成的计数集合，在V′中逐渐形成{g1,…,gt,gt+1}的所有子集V′求出的φ(V′)形成的计数集合。

{g1,…,gt,gt+1}中所有子集可分为两种，一种是不包含gt+1的子集V，显然这些子集就是{g1,…,gt}的所有子集。它们求出的φ(V)形成的计数集合就是V。由归纳前提“取gt后，到步骤（13）时，V及V′中的内容是{g1,…,gt}的所有子集V求出的φ(V)形成的计数集合”，所以步骤（3）取gt+1时，这种不包含gt+1的子集求出的φ(V)形成的计数集合已在V′中。

另一种是包含gt+1的子集V′，显然V′可写成V∪{gt+1}，其中V不含gt+1，于是V是{g1,…,gt}的某个子集。这样所有包含gt+1的子集V′，应是{g1,…,gt}的所有子集分别添上gt+1而成。于是每个φ(V′)都可写成φ(V∪{gt+1})，其中V是{g1,…,gt}的子集。然而由推论1知，φ(V∪{gk+1})=φ(V)⋂φ(gk+1)，所以所有φ(V′)可由φ(gt+1)分别与{g1,…,gt}的所有子集V的φ(V)求交而得到。

由于{g1,…,gt}的所有子集V的φ(V)的计数集合是V。而所有φ(V′)可由φ(gt+1)分别与V的所有(φ(V),k)中的φ(V)求交而得到。于是就在步骤（4）依次取V的所有(φ(V),k)，在步骤（5）求φ(gt+1)与(φ(V),k)中的φ(V)的交，并将其用R表示：R=φ(V)⋂φ(gt+1)。

由于(φ(V),k)的计数值为k，说明{g1,…,gt}的所有子集中相同值的φ(V)有k个，所以R也产生了k个。

分两种情况，若V′中没有左部为R的元素(R,k′)，且R≠∅，则将(R,k)添加到V′中（步骤（9））。若V′中已有一个(R,k′)则将它与(R,k)合并，在V′中用(R,k′+k)替换(R,k′)（步骤（7））。

于是在步骤（4）到步骤（12）的循环完成后，第二种包含gt+1的子集V′求出的φ(V′)也全部按计数集合的形式加入到V′中，所以到步骤（13）时，V′中的内容（从而V中的新内容），将是{g1,…,gt,gt+1}的所有子集V′求出的φ(V′)形成的计数集合。

这样由归纳法知，当取完gn后V中的内容是G的所有子集V求出的φ(V)形成的计数集合。

按定义4，value是对G≠∅求和，所以求和前应将V中初始的(φ(∅),1)删掉。由定义3知φ(∅)=U，因为有一些粒可能使用了所有项目，他们的φ也是U，所以V中初始的(φ(∅),1)，即(U,1)，到最后可能都成了(U,k)，为了对G≠∅求和，于是步骤（16）将(U,k)换为(U,k-1)。

k个S集合的元素个数应是|S|×k，于是步骤（17）到步骤（19）向value累加计数集合V的元素个数，累加得到的值除以m就是大数据的价值。

定理5 算法1的运算复杂度是O(2n)。

证 如果取gt时V中有T个元素，那么执行完步骤（4）到（12）后，最不利情况是V中将有2×T个元素。于是取完g1到gn后，步骤（3）到（14）的运算总次数，最不利情况将是O(2n)。显然步骤（17）到（19），运算总次数最不利情况也是O(2n)，所以整个算法的运算复杂度也是O(2n)。

因此，在实际工作中，选合适的粒度进行计算是十分重要的。

4 大数据价值计算实例应用

以一个远程智慧医疗的大数据作为应用实例。

大数据D={d1,d2,d3,…,d1034}是一个远程智慧医疗的大数据，其中d1,d2,d3,…,d1034是远程医疗传送的病人的各种文件，把d1,d2,d3,…,d1034按两种合适的粒度进行划分：

G1={g1,g2,g3,g4,g5,g6,g7,g8,g9}，其中g1是病人的自然信息表、g2是病人的患处外部影像、g3是病人的患处内部影像、g4是特殊患者生活行为跟踪、g5是病人住院病例、g6是病人的饮食报表、g7是病人的日常状态文档、g8是病人的血、尿检验报告、g9是其他。

G2={g1,g2,g31,g32,g33,g4,g5,g6,g7,g8,g9}，其中g1,g2,g3,g4,g5,g6,g7,g8,g9的意义与G1相同。而g31是病人的患处X光照片、g32是病人的患处CT影像、g33是病人的患处磁共振影像，它们是G1中的g3的细化。

选取使用单位U={u1,u2,u3,u4,u5,u6,u7,u8,u9}，其中u1是医疗单位、u2是医疗设备生产企业、u3是养老院、u4是药品研究院、u5是药品销售单位、u6是食品生产部门、u7是服装生产部门、u8是保险公司、u9是陪护、家政服务公司。

G1的使用关系A1如表4所示。

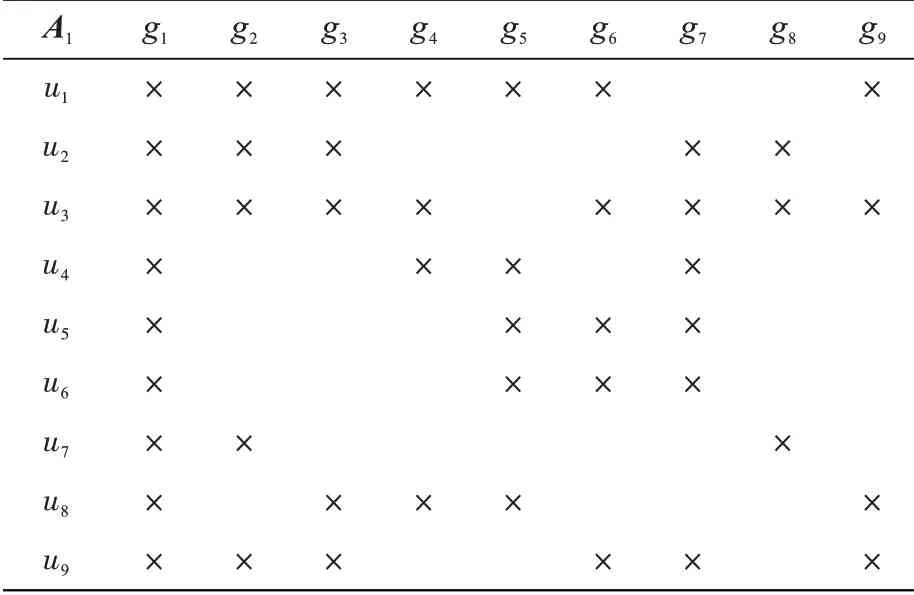
表4 远程医疗的使用关系Tab.4 Usage relationship of telemedicines

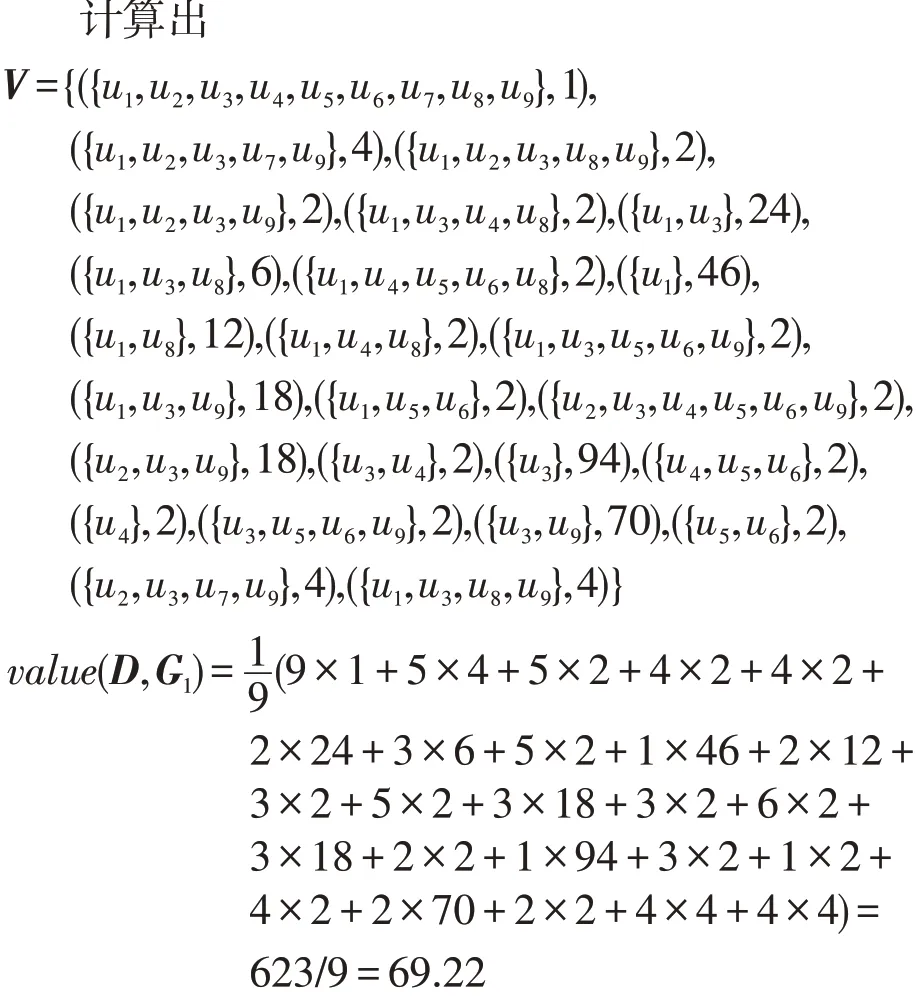
G2的使用关系A2如表5所示。

表5 远程医疗的使用关系的细化Tab.5 Refinement of telemedicine usage relationships

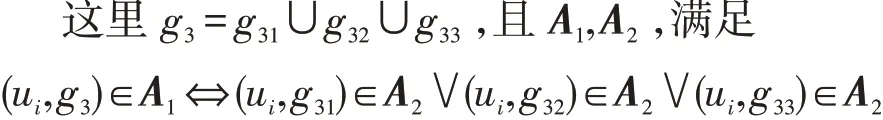
所以A2是A1的细化。

计算出

G3的使用关系A3如表6所示。

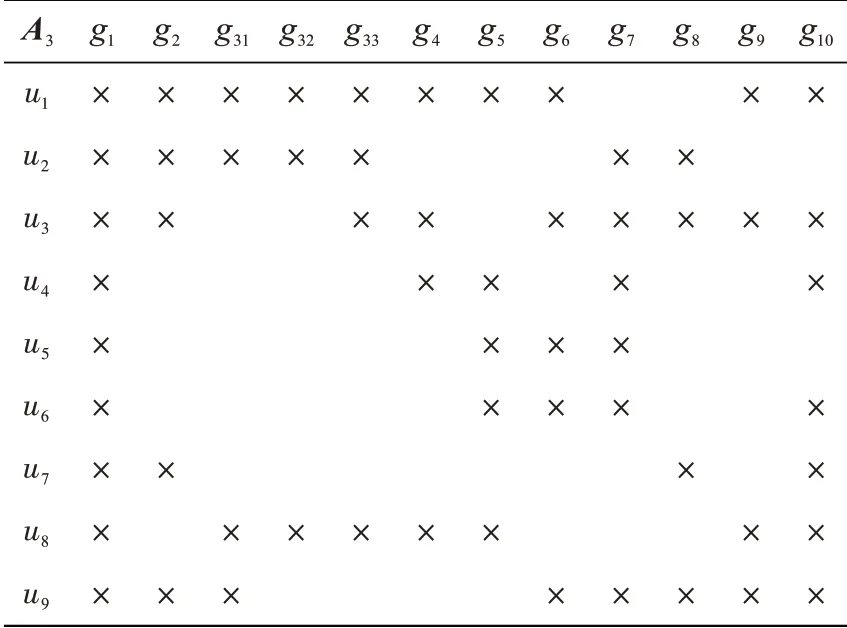
表6 远程医疗的使用关系的细化并扩充Tab.6 Refinement and expansion of telemedicine usage relationships

计算出

以上展示了在实际问题中基于粒计算及使用关系的大数据价值的计算过程。

经统计，按算法1，对于粒度G1有168个φ(G)=∅的子集G不被存入，其余344个子集，由于φ(G)相同的采用计数形式，所以也只需存入25个。对于粒度G2有1 230个φ(G)=∅的子集G不被存入，其余818个子集，由于φ(G)相同的采用计数形式，所以也只需存入35个。对于粒度G3有2 520个φ(G)=∅的子集G不被存入，其余1 576个子集，由于φ(G)相同的采用计数形式，所以也只需存入45个。显然，算法1极大地减少了计算工作量。

按算法1，粒度变细算出的价值有所增加，数据量加大算出的价值也有所增加，符合粒度单调性和数据量单调性规律。

5 结论

本文认为大数据价值在于应用，应用的次数越多，大数据价值越大。因此，本文是首次提出根据大数据的应用次数来计算大数据的价值。“粒计算”被列为非传统处理大数据的第一方法。本文在对大数据进行粒化的基础上，提出了基于“粒”及“粒的子集”使用次数的大数据价值计算方法，这是受形式概念理论启发给出的一种全新的计算方法。并证明了该方法计算出的大数据价值能满足粒度单调性以及数量单调性。分析了该算法的时间复杂度，得出了计算大数据价值时选择适当粒度的重要性，并给出了计算实例。

大数据价值计算是一个全新课题，未来进一步研究包括：（1）对更多的使用形式研究计算方法；（2）对计算算法进一步改进，降低复杂度；（3）对粒度的划分进一步研究，使粒度间转换更方便；等等。总之大数据价值计算是非常有意义的，将应用于更广阔的领域。