素数域椭圆曲线密码点乘的高性能硬件实现
高巍,骆宜萱,李佳琨,吴海霞 (北京理工大学 信息与电子学院,北京 100081)
椭圆曲线密码(elliptic curve cryptography,ECC)是一种基于椭圆曲线离散问题难解性的非对称加密算法,由Neal Koblitz[1]和Miller[2]于1985年分别提出.与常见的非对称加密算法RSA加密相比,ECC算法能使用更短的密钥长度达到相同的安全性能.ECC算法的优势使得它在密码学领域得到了越来越广泛地关注.在ECC算法中,最主要的运算步骤为椭圆曲线上的点乘.点乘作为ECC算法的核心,直接决定了ECC算法的性能,是ECC算法研究与实现的主要内容.
随着如今网络安全设备对密码运算速度需求的增长[3],软件实现的点乘算法已无法满足处理速度要求,点乘算法的硬件实现成为了研究的首选.在点乘算法的硬件实现中,二进制域点乘硬件的算术逻辑单元(arithmetic and logic unit,ALU)由异或运算组成,素数域点乘硬件的ALU由模运算组成.模运算ALU使得素数域点乘硬件能额外计算同为模运算的RSA加密.素数域点乘硬件底层ALU的通用优势使得它广泛应用于如今的嵌入式系统和物联网安全设备中,如NFC,oneM2M, WAVE等[4].这些系统和安全设备都具有有限的硬件资源,同时也需要较高的计算速度,使得点乘的高性能硬件实现成为了一项新的挑战.
近年来,多个素数域点乘高性能硬件设计被相继提出[5-9].Marzouqi[5]使用冗余符号数计算法提高了点乘的速度,但算法消耗了大量的硬件资源; Loi[6]实现了可重构的高性能点乘硬件,但是ALU位宽只有17位,并且使用了一个复杂的状态机,状态机的跳转消耗了大量LUT资源;Roy[7]的轻量化设计使用了存放固定控制指令的指令ROM代替状态机,节约了复杂状态机占用的硬件资源,但设计中使用大量的BRAM来交换LUT资源,留给FPGA中其他设计的片内存储能力变小.基于上述设计的优缺点,本文提出了一种高位宽ALU、指令ROM进行控制的高性能256位ECC点乘硬件,合理地对计算速度与硬件资源做出权衡,整体性能得到大幅度提升.
1 ECC的数学原理
ECC的算法整体结构[10]如图1所示,从上到下分为协议层、点操作层、模运算层.
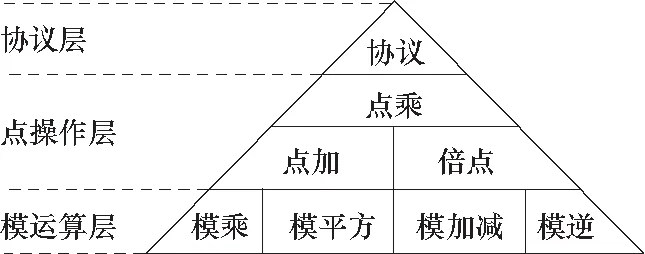
图1 ECC算法结构Fig.1 ECC algorithm structure
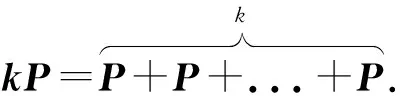
y2=x3+ax+b
(1)
在这条椭圆曲线上,定义两点P=(x1,y1)和Q=(x2,y2),可以得到点加的仿射坐标P+Q=(x3,y3)与倍点的仿射坐标2P=(x4,y4).将两点的坐标代入椭圆曲线公式中可以得到点加与倍点的仿射坐标计算公式.
(2)
(3)
(4)
(5)
素数域ECC算法中的坐标计算均是素数域中的模运算,包括模加减、模乘、模平方、模逆4种.模运算需要首先计算加减法、乘法、平方、除法,再对结果进行选定的素数p的模约减.素数域ECC选取的素数p一般为美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)推荐的NIST素数.本文中选用的素数为256位NIST素数p256=2256-2224+2192+296-1,所有的模运算最终都需要约减至小于p256.
2 点乘的硬件实现算法
2.1 点操作层
传统Left-to-Right点乘[11]如算法1所示,点乘中的点加与倍点是仿射坐标下的点加与倍点,通过公式(2)~(5)进行计算,然而公式中存在除法,不易进行硬件实现.本文改进了传统的Left-to-Right点乘算法,使点乘算法的速度得到了提升.
算法1 传统Left-to-Right点乘算法
已知:k=(kl-1,kl-2,…,k2,k1),P∈E
待求:kP
1.Q←0
2. forifroml-1 to 0
3.Q←2Q(倍点)
4. ifki=1
5.Q←P+Q(点加)
6. end if
7. end for
8. ReturnQ
为了避免公式中硬件不易计算的除法,本文中点加和倍点使用投影坐标系代替仿射坐标系.Darrel Hankerson[10]介绍了4种投影坐标系下点加与倍点的计算方法和计算时间.本文使用了其中计算速度最快的Jacob投影坐标倍点和Jacob仿射混合坐标点加,如算法2和算法3所示.除了Jacob仿射混合坐标点加中的(X2,Y2)以外,这一套倍点、点加算法的输入输出均在Jacob投影坐标系下.在Left-to-Right点乘中,点加的(X2,Y2)正好始终为仿射坐标下的P点,因此Left-to-Right点乘可以连续地进行Jacob投影坐标倍点和Jacob仿射混合坐标点加,运算过程中的所有点均不需要进行坐标转换.
算法2 Jacob投影坐标倍点
已知:Jacob坐标(X1,Y1,Z1),椭圆曲线常数a
待求:(X3,Y3,Z3)=
2(X1,Y1,Z1)

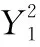
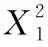
4.T1←a·Y3
5.T3←Z3+Z3
6.T1←T1·Y3
7.T2←X1·X3
8.T3←T3+Z3
9.Y3←T3+T1

11.T3←T2+T2

13.Z3←T3+T3
14.T3←Z3+Z3
15.X3←T1-T3
16.T1←Y1·Z1
17.T4←Z3-X3
18.T3←T2+T2
19.T2←T4·Y3
20.T3←T3+T3
21.Y3←T3+T3
22.Z3←T1+T1
23.Y3←T2-Y3
24. ReturnX3,Y3,Z3
算法3 Jacob仿射混合坐标点加
已知:Jacob坐标(X1,Y1,Z1),仿射坐标(X2,Y2)
待求:(X3,Y3,Z3)=
(X1,Y1,Z1)+(X2,Y2)

2.T2←T1·Z1
3.T1←T1·X2
4.T2←T2·Y2
5.Z3←X1-T1
6.T2←T2-Y1

8.T1←Z3·T4
9.T4←X1·T4

11.Y3←T1·Y1
12.T3←T4+T4
13.X3←X3+T1
14.X3←X3-T3
15.T4←X3-T4
16.T4←T4·T2
17.Z3←Z1·Z3
18.Y3←T4-Y3
19. ReturnX3,Y3,Z3
由于引入了投影坐标系,开始Left-to-Right点乘算法前需要先将仿射坐标下的Q点通过算法4转换到Jacob投影坐标,在完成所有的点加和倍点之后,通过算法5将Jacob坐标下的结果Q转换回仿射坐标得到最终的点乘结果.
算法4 Jacob投影坐标转换
已知:仿射坐标(x,y)
待求:Jacob投影坐标(X,Y,Z)
1.Z=1
2.X=xZ2=x
3.Y=yZ3=y
算法5 仿射坐标转换
已知:Jacob投影坐标(X,Y,Z)
待求:仿射坐标(x,y)
1.x=X/Z2(模逆)
2.y=Y/Z3(模逆)
引入投影坐标系后,最终改进后的坐标转换Left-to-Right点乘算法流程如算法6所示.
算法6 改进的坐标转换Left-to-Right点乘
已知:k=(kl-1,kl-2,…,k2,k1),P(x,y)∈E
待求:k*P(x,y)
1.Q(x,y)←0
2.Q(X,Y,Z)←Q(x,y) (算法4)
3. forifroml-1 to 0
4.Q(X,Y,Z)←2Q(X,Y,Z) (算法2)
5. ifki=1
6.Q(X,Y,Z)←P(x,y)+Q(X,Y,Z)(算法3)
7. end if
8. end for
9.Q(x,y)←Q(X,Y,Z) (算法5)
10. ReturnQ
2.2 模运算层
2.2.1模加减
本文采用的模加减算法为Omura[12]提出的模加减算法,如算法7所示.该算法适合进行硬件实现,只需要两个加法器分别计算A+B与(A+B)-p,通过二选一选择器输出最终的结果.同时改变两个加法器的加减极性可以计算模减.
算法7 Omura模加减法
已知:均为m位的A、B、素数p,且A 求:S1=A+B(modp),S2=A-B(modp) 2.2.2模乘与模平方 本文中模乘算法分为两步.第一步进行分段相乘,计算未约减的乘法结果.分段相乘法将256位乘法拆分为适合DSP计算的64位乘法,如算法8所示.第二步将分段相乘完成后的结果进行NIST快速约减[13],如算法9所示.NIST快速约减法包括14次模加减,因此本文通过复用Omura模加减的硬件模块来完成NIST快速约减.硬件的复用使得模约减算法的实现消耗了更少的硬件资源. 为了节省硬件资源,模平方计算通过复用模乘硬件模块来完成.将分段相乘模块的输入x,y改为输入x,x可以进行模平方运算. 算法8 分段相乘算法 已知:x 待求:c=x*y 1.x=(x3,x2,x1,x0)(xi为64位) 2.y=(y3,y2,y1,y0)(yi为64位) 3.c=(c7,c6,c5,c4,c3,c2,c1,c0)(ci为64位) 4.forifrom 0 to 3 5.forjfrom 0 to 3 6.(ci+j+1,ci+j)=xi*yj+(ci+j+1,ci+j) 7.end for 8.end for 9.Returnc 算法9p256的NIST快速约减法 已知:p256,512位的c 待求:s=c(modp256) 1.x=(x3,x2,x1,x0)(xi为64位) 2.定义12个小于p的256位数: s1=(c7,c6,c5,c4,c3,c2,c1,c0) s2=(c15,c14,c13,c12,c11,0,0,0) s3=(0,c15,c14,c13,c12,0,0,0) s4=(c15,c14,0,0,0,c10,c9,c8) s5=(0,c13,c15,c14,c13,c11,c10,c9) s6=(c8,0,0,0,0,0,0,0) s7=(0,c8,0,0,0,c13,c12,c11) s8=(c10,0,0,0,0,0,0,0) s9=(0,c9,0,0,c15,c14,c13,c12) s10=(c11,0,0,0,0,0,0,0) s11=(c12,0,c10,c9,c8,c15,c14,c13) s12=(c13,0,c11,c10,c9,0,c15,c14) 3.s=s1+2s2+2s3+s4+s5+s6-s7-s8-s9-s10-s11-s12(modp) 4.Returns 2.2.3模逆 本文中的模逆采用费马小定理[14]进行计算: Z-1=Zp-2modp (6) 费马小定理模逆的原理是将除法转换为模乘与模平方.本文中只有算法5需要计算Z-3,Z-2两个模逆,使用同时模逆算法[10]可以一次模逆运算得到这两个模逆结果.同时模逆算法如算法10所示. 算法10 同时模逆算法 已知:Z,素数p,且Z 待求:Z-3modp,Z-2modp 1.Z-3←Zp -4(modp) 2.Z-2←Z-3*Z(modp) 3. ReturnZ-3,Z-2 算法的第一步可以由费马小定理推导得到 Z-3=Z-1*Z-1*Z-1(modp)= Zp -2*Z-1*Z-1(modp)= Zp -4(modp) (7) 综上,整个模运算单元只需要Omura模加减器和乘法器两个计算模块就可以完成模加减、模乘、模平方、模逆4种基本模运算.硬件模块的复用减少了硬件资源的消耗,实现了硬件系统的轻量化. 系统的硬件总结构如图2所示,数据输入之后执行改进的坐标转换Left-to-Right点乘算法(算法6).算法中需要的倍点、点加、模逆操作均通过复用同一个点操作模块完成.模块的逻辑由一个状态机进行控制,状态机将根据点乘算法跳转到不同的状态,输出相应的点乘操作指令,之后将操作指令输入到点操作模块依次进行倍点、点加、模逆操作,最终完成点乘得到kP的x,y仿射坐标. 图2 点乘的硬件总结构Fig.2 The hardware structure of point multiplication 点操作模块负责运算倍点、点加、模逆3种操作.从算法2~5和算法10可知,倍点、点加、模逆操作都是由一定顺序的模乘与模加减组成.本文使用3个指令ROM分别控制3种操作下模运算ALU的计算类型与顺序来完成倍点、点加、模逆. 指令ROM是一个顺序存储了每周期控制指令的ROM.当运算开始时,指向地址的指令计数器开始自加,指令ROM顺序输出每周期的控制信号.与状态机进行控制相比,指令ROM避免了状态机跳转时的大量选择器,消耗了更少的资源.对于倍点、点加、模逆操作的控制逻辑来说,每周期的操作指令、RAM读写地址等控制信号都是固定的,非常适合使用指令ROM来顺序存储每周期的控制指令.点操作模块使用指令ROM替代状态机大幅度节省了控制逻辑的硬件资源. 图3展示了点操作模块的硬件结构.数据输入、数据输出、操作指令控制信号均由上层的点乘模块进行控制.操作指令控制信号通过选择指令ROM来选择执行倍点、点加或模逆操作.3种操作复用同一个模运算ALU,并使用了一个RAM来缓存计算过程的中间变量X1、Y1、Z1、X2、Y2、T1、T2、T3、T4以及计算过程中需要使用的常量0. 图3 点操作模块的硬件结构Fig.3 The hardware structure of point doubling,point addition and modular inversion module 点操作模块中的模运算ALU负责进行所有的模运算,其整体结构如图4所示,包括模约减模块、模加减器和乘法器. 图4 模运算ALU的硬件结构Fig.4 The hardware structure of modular ALU 通过改变ALU的输入控制信号,ALU将调度不同的模块,从而实现不同的运算功能.本文的模运算ALU模块一共可以计算256位模乘、256位乘法、64位乘法、256位模加减、256位加减法、128位模加减和128位加减法.多运算模式的ALU使得点乘模块可以作为硬件加速器为其他系统提供多样化的运算加速.此外,ALU的高位宽还减少了模运算所需的周期数,加快了模运算的计算速度.模运算作为点乘中最主要的基本运算,直接决定了点乘的计算速度,模运算的高速性使得点乘计算的高速性得到了保证. 3.3.1模约减模块 模运算ALU中的模约减模块负责实现NIST快速取模算法(算法9),其硬件结构展示在图4中.进行NIST快速取模时,首先将乘法器中RAM输出的结果通过4个选择器与二级寄存器拼接为NIST快速取模算法中每一周期的si,之后si被依次输入到模加减模块进行累加.与点操作模块相同,模运算ALU中快速取模的控制信号由指令ROM输出.指令ROM顺序输出每周期选择器的Sel信号、RAM的读地址、模加减器的加减极性控制信号等来控制NIST快速取模算法的逻辑,从而实现模乘运算. 3.3.2模加减器 模运算ALU中的模加减器负责实现Omura模加减算法(算法7).使用256位加法器实现该算法的硬件结构如图5所示.然而此结构的进位链过长,会导致系统时钟频率慢. 图5 256位加法器实现的模加减器的硬件结构Fig.5 The hardware structure of the modularadder-subtractor implemented by a 256-bit adder 为了提高系统时钟频率,本文提出了图6的模加减器结构.该结构将256位加法器拆分为两个128位加法器,并在加法器后插入寄存器.通过流水地向加法器输入a与b的高位和低位,输出选择器会流水地输出a+b或a+b-p的高位和低位,从而实现256位模加法.同时改变加法器的加减极性控制信号可以进行模减运算.该结构采用的加法器拆分方法将进位链缩短至原来的1/2,使加法器进位链不再是系统的最差路径. 图6 本文提出的模加减器硬件结构Fig.6 Proposed hardware structure of modular adder-subtractor 3.3.3乘法器 模运算ALU中的乘法器负责使用分段相乘算法(算法8)进行256位乘法,其基本单元为64位DSP乘法器IP核.图7展示了乘法器的硬件结构,乘法器中所有的控制信号均通过指令ROM输出.根据分段相乘算法,x与y首先通过移位寄存器流水输入到DSP乘法器完成16次乘法.每次乘法得到的128位结果将进行累加,累加的结果会被缓存到寄存器和RAM中以进行后续的累加.为了避免读取RAM时地址不对齐的问题,本文使用了两个64位RAM进行高低位交错存储,将128位的乘法结果分为高低64位,分别存储在两个不同的RAM中.对于地址不对齐的128位数据,高低位交错存储法可以一周期同时读取两个RAM不同地址的高低位数据来组合得到需要的128位数. 图7 乘法器的硬件结构Fig.7 The hardware structure of multiplier 本文提出的点乘硬件设计通过Synplify Pro在Xilinx Virtex-5 FPGA上综合实现.资源使用量为2 684 LUT,16 DSP,4 BRAM,时钟频率达到150.2 MHz,完成一次点乘计算需要4.24 ms.与其他同为Virtex-5 FPGA实现的文献[5-9]相对比的结果如表1所示. 表1 不同设计的综合结果对比 为了综合考虑LUT、DSP与BRAM的资源占用量,本文先将DSP数量和BRAM数量转换为LUT数量,再与初始的LUT数量相加得到归一化LUT数量,最终比较归一化LUT数量来对比不同设计的硬件资源占用量.DSP与LUT的转换关系可以使用64位乘法器的综合结果得到.在Virtex-5 FPGA上,当使用DSP综合64位乘法器时,需要的DSP数为16;当使用LUT综合64位乘法器时,需要的LUT数为4 256,因此可以得到换算关系1DSP≈266LUT.BRAM与LUT的转换关系可以使用16K RAM的综合结果得到.在Virtex-5 FPGA上,综合一个16 K分布式RAM需要44个LUT,因此可以得到换算关系1BRAM≈44LUT.根据转换关系最终可以得到归一化LUT数量.为了更好地对比不同设计中资源与速度的权衡,性能的量化标准采用一个公认的性能测算公式,综合考量了硬件资源和计算速度[15]如下. (8) 该性能指标越高,表示系统总体效果越好.如表1所示,与计算速度最快的Marzouqi H[5]相比,本设计的计算速度慢46%,但硬件资源占用量低79%,整体性能指标提升了159%;与硬件资源占用量最少的Roy D B[7]相比,本设计的硬件资源占用量多110%,但计算速度快187%,整体的性能指标提升了37%.从对比结果可以看出,本文提出的高性能点乘硬件设计在减少资源的同时,兼顾了点乘运算的速度,整体的综合性能得到了显著地提升,最终以33.14的性能指标高于其他文献. 本文提出了一种高性能ECC点乘硬件结构.该硬件基于改进的Left-to-Right点乘算法,利用模块的复用与指令ROM减少了硬件资源消耗,并通过高位宽的ALU提高了点乘计算的速度,最终显著地提升了点乘系统的综合性能.3 素数域ECC点乘的高性能硬件实现
3.1 系统总结构
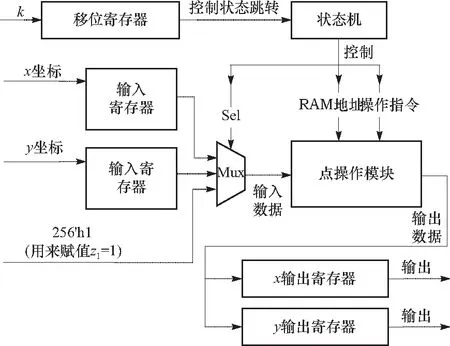
3.2 点操作模块
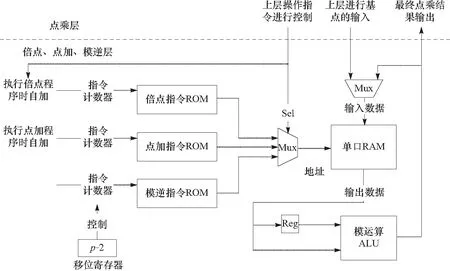
3.3 模运算ALU
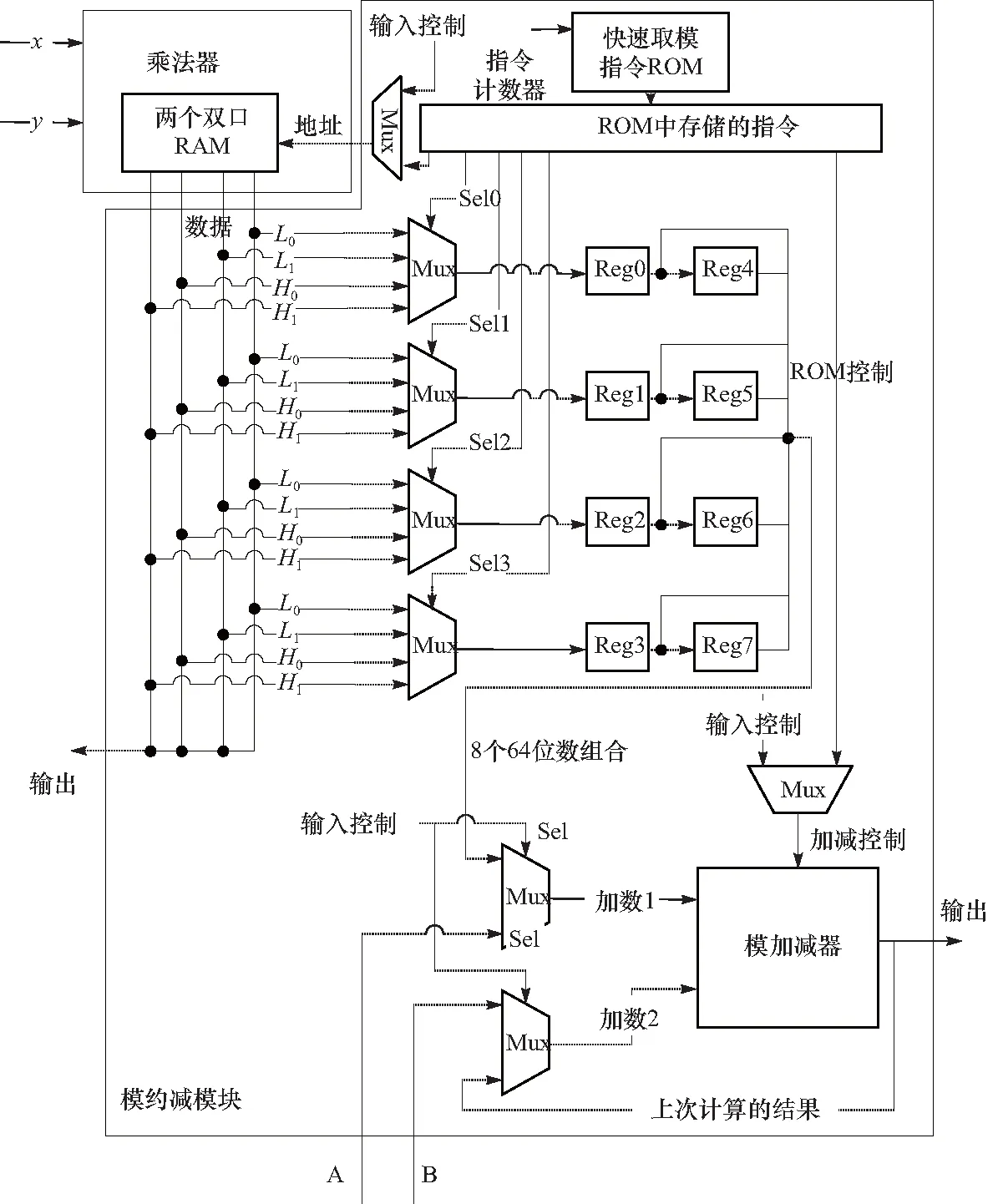
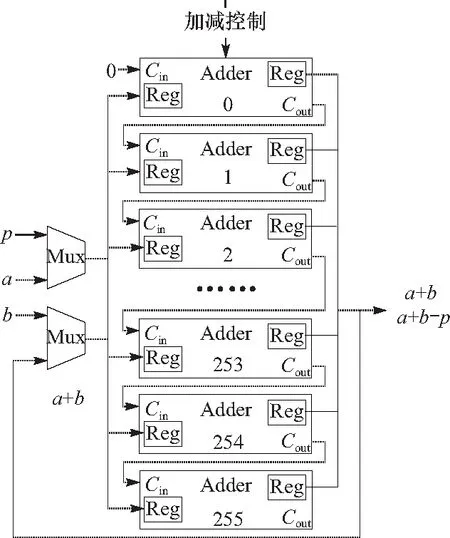
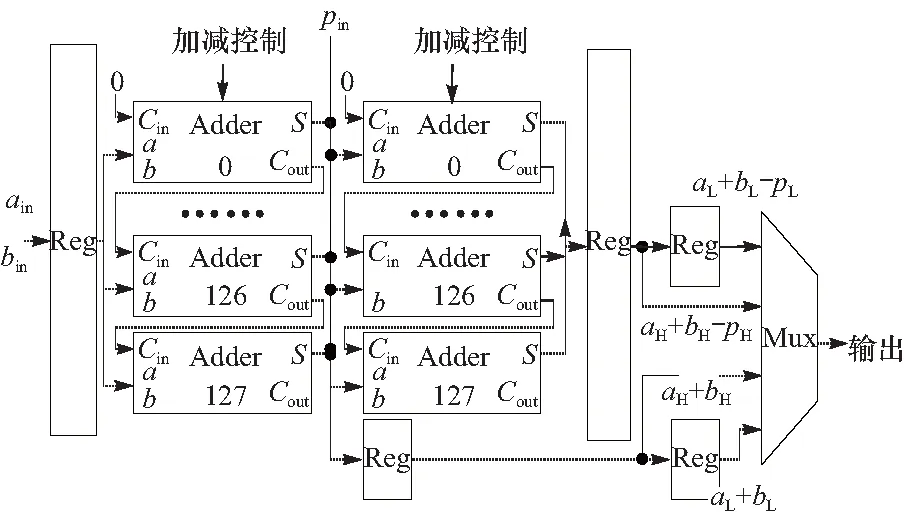
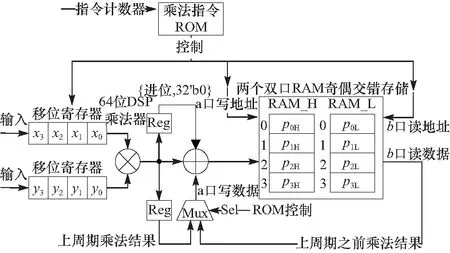
4 FPGA综合结果与对比
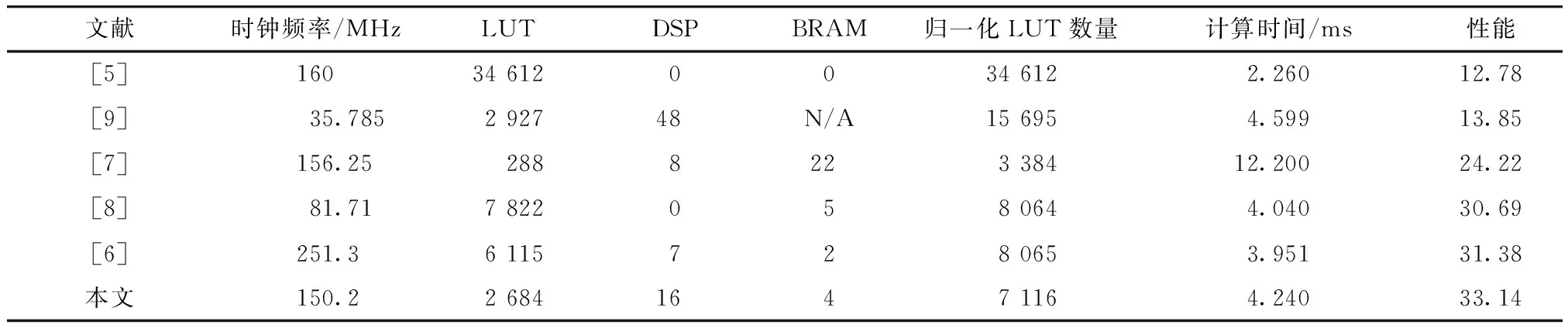
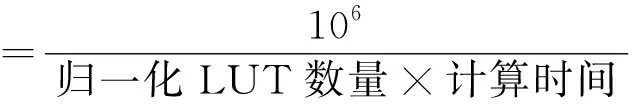
5 结 论

