液力变矩器通用特性及其匹配方法的研究

马惠臣，刘城,2，李娟，李晋 (.北京理工大学 机械与车辆学院，北京 0008；2.北京理工大学重庆创新中心，重庆 4047；.中国北方车辆研究所，北京 00072)

液力变矩器由于具有自适应变速变矩等优越特性而被广泛应用于车辆的自动变速器中，极大地简化了车辆的操纵，延长了传动部件的使用寿命[1].发动机与液力变矩器的匹配是整车动力传动系统匹配中最重要的一环，二者匹配的好坏会直接影响车辆动力传动的性能.

发动机与液力变矩器共同工作输入特性的确定是液力传动系统匹配计算和评估的关键，也是计算二者共同工作输出特性的基础.传统共同工作点的确定方法常采用解析或数值计算方法[2].随着计算机技术的发展，借助计算机建模语言[3-4]，可实现图形化匹配用户界面等多样式计算工具[5-6].神经网络和遗传算法等方法的提出[7-8]，提高了匹配模型的拟合精度，及数据分析的准确性[9].

传统的发动机与液力变矩器匹配过程中，均采用单一泵轮转速下的原始特性进行匹配，而车辆在实际运行过程中，发动机转速，即泵轮转速是不断变化的.在不同泵轮转速下，液力变矩器内部流动雷诺数、温度场分布等存在差异，故其液力特性是不同的，导致传统匹配方法产生一定的匹配误差，从而使得特性预测与实际工作状况有出入.同时，匹配计算多采用最小二乘法等数据处理方法，存在一定的累积误差.因此，有必要在发动机与液力变矩器的匹配过程中，考虑不同泵轮转速对液力变矩器特性的影响，构建更接近于实际运行工况的匹配模型，以提高发动机与液力变矩器匹配计算精度.

本文利用BP(back propagation)神经网络建立液力变矩器通用特性模型，借助液力变矩器有限外特性数据，实现任意泵轮转速、涡轮转速工况下液力变矩器特性的预测.同时建立基于通用特性的发动机与液力变矩器匹配计算模型，实现发动机与液力变矩器的准确匹配.

1 液力变矩器外特性试验

首先在液力变矩器牵引工况性能台架试验上，测试了其在不同泵轮、涡轮转速下的稳态液力性能.先根据传统匹配方法，利用泵轮转速1 800 r/min特性数据，获取发动机和液力变矩器共同工作时泵轮转速的大致范围为1 886～2 300 r/min，依此(图1)确定试验泵轮转速取值为nB=1 600，1 700，1 800，1 900，2 000，2 100，2 200，2 300 r/min.采用定泵轮转速(nB)的方法，在给定的系列泵轮转速下，通过调整涡轮转速(nT)模拟液力变矩器不同速比(i)的加减载循环工况，并利用传感器测得泵轮转速、泵轮转矩(TB)、涡轮转速和涡轮转矩(TT).

图1 获取泵轮转速的大致范围Fig.1 The approximate range of pump wheel speeds

2 传统匹配方法误差分析

传统匹配方法将发动机的净外特性与液力变矩器的负荷特性抛物线以相同的坐标比例绘制在一起，即得到发动机与液力变矩器共同工作的输入特性；计算净外特性曲线和负荷抛物线簇的一系列交点，并确定各交点转速下的转矩、输出功率等特性参数.

根据传统匹配方法，对不同泵轮转速下液力变矩器液力特性试验结果进行对比.按式(1)计算液力变矩器在不同泵轮转速下的液力性能参数.计算结果如图2，表明用单一泵轮转速下的特性去代替不同泵轮转速特性会造成液力特性存在较大误差.

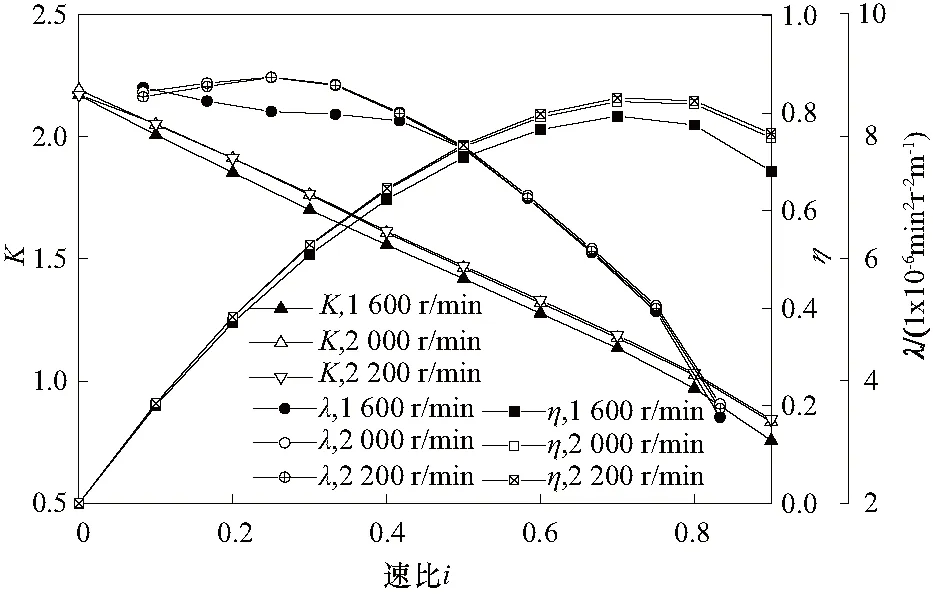
图2 不同泵轮转速液力特性曲线及相对误差Fig.2 Hydraulic character and relative errors in different speeds of pump

(1)

式中：K为变矩系数；η为液力变矩器传动效率；λB为泵轮转矩系数，min2/(m·r2)；ρ为液力变矩器工作油密度，kg/m3；g为重力加速度，m/s2；D为循环圆直径，m.

由于不同泵轮转速下原始特性中λ存在误差，导致同一转速比下，液力变矩器负荷抛物线与发动机转矩外特性相交点的转矩和转速不同(图3).泵轮转速2 200、2 000，1 600 r/min在不同速比下交点转矩转速的相对误差按式(2)计算(如图4).结果显示，在低速比下转矩和转速的相对误差较小，因此在外特性段交点转矩的相对误差较小，最大误差在3%以内；在高速比工况下(i>0.6)，受发动机调速段大斜率的影响，泵轮转矩误差较大，最大相对误差可达50%.这种大的误差与液力变矩器和发动机匹配情况相关，如果液力变矩器与发动机共同工作区域只在发动机外特性段，那么相对匹配误差会较小，如果液力变矩器与发动机共同工作区域匹配在了发动机调速段，相对误差则会迅速增加.

图3 不同泵轮转速下共同工作输入特性Fig.3 Input characteristics in different speeds of pump

图4 输入特性相对误差Fig.4 Relative error of input characteristics

(2)

式中：δ为相对误差；X为任意计算相对误差的参数.

除了由于λ的不同造成的共同工作点误差，不同泵轮转速下液力变矩器的变矩比、效率也不一致，利用式(3)进行传统匹配计算时，进一步扩大了其输出特性中输出转矩MT及输出功率PT的累计误差.

(3)

图5为在不同泵轮转速下利用传统方法匹配后得到的共同输出特性曲线.泵轮转速2 200 r/min、2 000 r/min与1 600 r/min输出特性指标的相对误差按式(2)计算.相对误差计算结果如图6所示，随着涡轮转速的增加，在外特性段输出扭矩的相对误差在30%以内，输出功率的相对误差在27%以内，表明传统匹配方法由于不考虑泵轮转速的影响可能导致较大的匹配误差，特别在高速比工况下，由于发动机调速段的影响，与实际发动机和液力变矩器的共同工作状态差别将进一步放大.

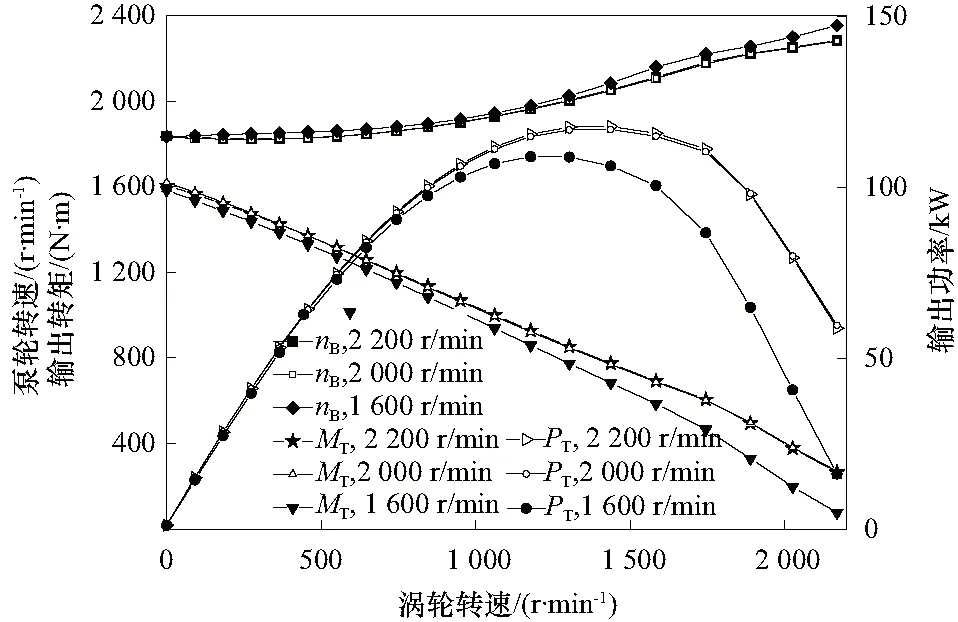
图5 输出特性曲线Fig.5 Output characteristics

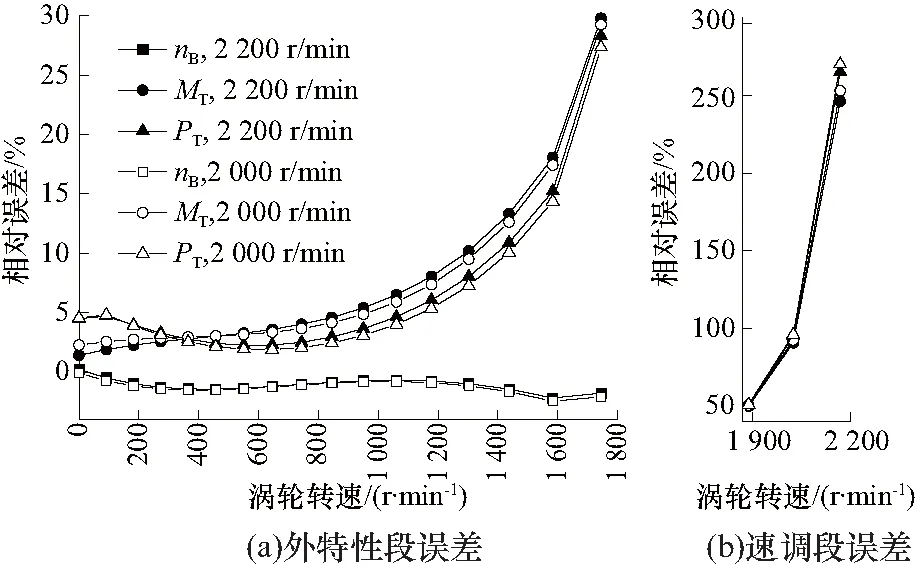
图6 输出特性相对误差曲线Fig.6 Relative error of output characteristics

必须指出，上述的误差统计及误差变化规律，受液力变矩器与发动机的匹配参数影响较大，特别是调速段对匹配结果存在较大影响，对于不同类型以及特性的液力变矩器，误差变化规律是不同的，但总的来说，传统的利用单一泵轮转速进行匹配的方法导致输出特性在外特性工况约能引起25%左右的匹配误差，高速比工况的误差则会更大.

3 液力变矩器通用特性预测模型

3.1 液力变矩器通用特性建模

BP神经网络法以其独特的自适应、高度非线性、泛化能力强等特征，与传统线性拟合相比，更加适合用来处理液力变矩器的试验数据，函数拟合的精度明显更高[10]，且不需要对试验数据进行筛选、去噪，而且在多维数据处理方面拟合精度较高，因此本文利用BP神经网络在有限外特性试验数据基础上构建液力变矩器通用特性模型.采用Sigmoid可微函数作为神经元的传递函数，实现输入和输出之间的任意非线性映射，Sigmoid函数的输出接近高等生物神经元的信号输出形式，能够模拟不同形式的输入和输出映射的非线性特征.且该函数对学习中产生的噪声成分反应不敏感，从而能够体现出大量数据样本的主流方向.采用三层BP神经网络对液力变矩器的外特性试验数据进行处理，并构建其泵轮转矩和涡轮转矩神经网络，如图7所示[11].

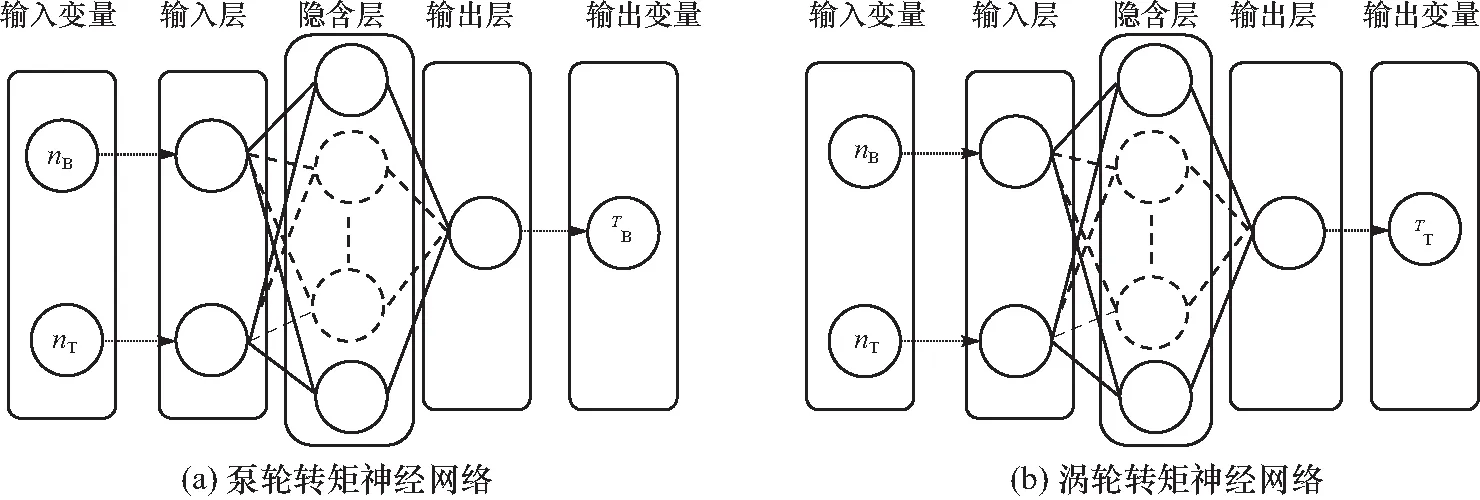
图7 BP神经网络模型Fig.7 BP neural network model

神经网络模型反映液力变矩器泵轮转矩、涡轮转矩分别与泵轮转速、涡轮转速的映射关系f，亦即

TB=fB(nB,nT)

(4)

TT=fT(nB,nT)

(5)

隐含层节点数的确定对神经网络模型的精度和鲁棒性具有较大影响，首先根据经验公式[12]，通过输入层节点数与输出层节点数确定隐含层节点数范围：

(6)

式中：Nhid为隐含层节点数；Nin、Nout分别为输入、输出层节点数；α为1～10之间的常数.

由于两个神经网络模型均为2输入1输出模型，故隐含层节点数范围为2～11.由于神经网络具有较强的非线性和不确定性，即使同一隐含层节点数对相同数据进行训练时其输出结果可能会有不同，因此采用多次重复训练的方法，对统计结果进行分析，选取最佳隐含层节点数.在同一个隐含层节点数下进行20次重复训练，记录模型的决定系数R2(如图8).决定系数越接近于1，表示模型的拟合效果越好.

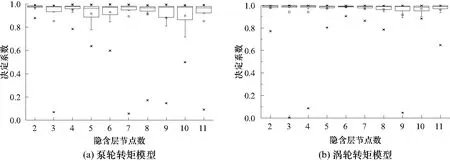
图8 不同隐含层节点数的决定系数Fig.8 The determination coefficient of nodes in different hidden layers

通过不同节点数决定系数的统计分析，确定了泵轮转矩和涡轮转矩模型的隐含层节点数分别为2和6，两个模型在此节点下决定系数分布的均值和中位数都最高，并且更加稳定，因此网络的结构分别为2-2-1和2-6-1.

确定各模型隐含层节点后，以1 600、1 800、2 000、2 200 r/min泵轮转速下的数据作为训练集，对神经网络模型进行训练；以1 700、1 900、2 100、2 300 r/min泵轮转速下的数据作为测试集，测试该神经网络模型的预测精度.

3.2 液力变矩器经验公式修正模型

对一系列几何相似的液力变矩器，当泵轮转速nB有效直径D不同时，原始特性并不相同，为有效表达一定范围内不同的泵轮转速和有效直径液力变矩器的性能，传统方法提出了修正经验公式计算nB和D对变矩比K的影响.以下标m代表模型液力元件，下标s代表实物液力元件.

(7)

必须指出，这类修正公式都有一定的适用性，仅适用于某种形式和一定范围内不同的泵轮转速nB和有效直径D数值的液力变矩器.

3.3 模型误差分析

3.3.1通用特性模型误差分析

图9 BP神经网络在不同泵轮转速工况下转矩相对误差图Fig.9 Torque relative error graphs of BP neural network under different pump wheel speeds

3.3.2修正公式模型误差分析

利用泵轮转速2 000 r/min作为模型液力元件，根据修正公式求得不同泵轮转速(1 600，1 700，1 800，1 900，2 100，2 200 r/min)下不同速比的Ks，结合公式-MT=KsMB，获得一系列不同泵轮转速以及不同速比下的液力变矩器输出转矩值.并与试验数据结果进行对比分析，估计模型的预测精度(如图10).结果显示，在不同工况下，修正模型中的泵轮转矩最大相对误差为12%，平均相对误差达到5%.

图10 修正模型不同工况输出转矩相对误差图Fig.10 Relative error graph of torque in different conditions of corrected model

由此可知，通用特性模型相比于经验公式修正模型，其预测精度有较大的提升.由于修正模型中的修正经验参数需要一定量的试验数据进行修正，且适应性有限，对数据的预测精度相对通用特性模型较差，难以满足发动机与液力变矩器匹配要求.

4 发动机与液力变矩器通用特性匹配模型

4.1 匹配模型建模

通用特性匹配计算流程如图11所示.

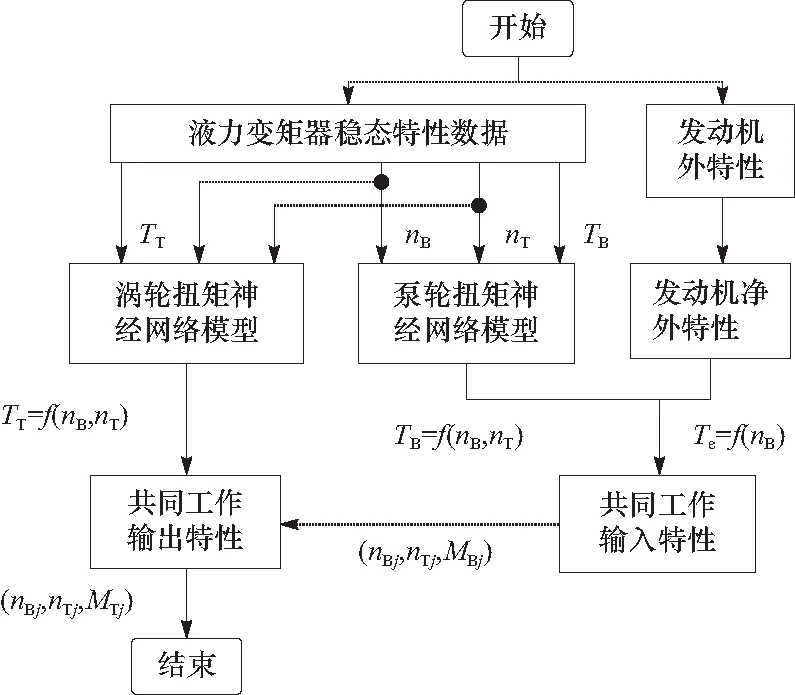
图11 通用特性匹配模型计算流程Fig.11 Calculation process of general characteristic matching model

利用曲面表征液力变矩器泵轮转矩和涡轮转矩在不同泵轮、涡轮转速下的特性，结合发动机的净外特性转矩输出曲面，利用二分法将曲面求交线的问题转化为不同涡轮转速下曲线求交点的问题.在某一定涡轮转速nT下，可利用液力变矩器通用特性模型获得泵轮转矩TB特性曲线TB=g(nB).利用发动机净外特性转矩曲线Te=f(nB)，则求交点问题可转化为下式.

F(nB)=g(nB)-f(nB)=0

(8)

借助二分法进行多次迭代计算，当F(δk)<10-3时，δk即为F(nB)=0的近似解.进而得到一系列交点坐标(nBj，nTj,MBj)(j为涡轮转速点的个数，j=1,2,3,……).将该系列点依次相连，即为共同工作输入特性曲线.将nBj和nTj代入涡轮转矩预测模型中，得到对应涡轮转矩点(nBj,nTj,MTj)，即共同工作输出特性曲线.

4.2 匹配结果分析

图12为传统匹配方法和通用特性匹配方法的输出转矩与泵轮转速的对比情况.可以看出，由于考虑了泵轮转速对液力变矩器特性的影响，通用特性模型匹配方法预测的输出转矩结果基本处于传统方法最高转速和最低转速匹配输出结果之间波动.同时，传统匹配方法利用单一泵轮转速下的能容系数考虑了负载对发动机转速的影响，但由于不同泵轮转速下液力变矩器的能容系数是有变化的，因此传统方法在进行匹配后出现不一致的情况.新方法综合考虑了负载(涡轮转速)及泵轮转速对发动机输出特性的影响，更符合实际匹配工况.

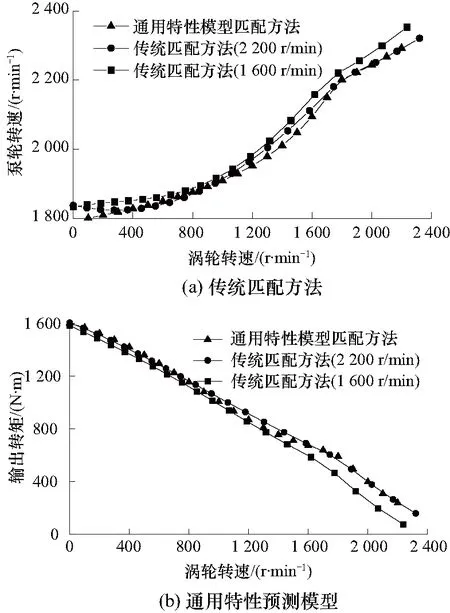
图12 模型输出特性对比Fig.12 Comparison of output characteristic

4.3 匹配模型具体实施案例

根据本文中提出的发动机与液力变矩器通用特性匹配模型，对某5吨装载机用液力传动系统进行匹配，获得装载机牵引力特性，并与传统匹配方法进行对比.整车参数如表1所示.各个方法下驱动力特性中最高车速以及最大牵引力如表2所示.采用传统方法进行匹配时，选取不同泵轮转速下的原始特性会导致装载机的牵引力特性形成较大误差，而通用特性匹配方法的匹配结果更符合实际的装载机牵引力特性，如图13所示.

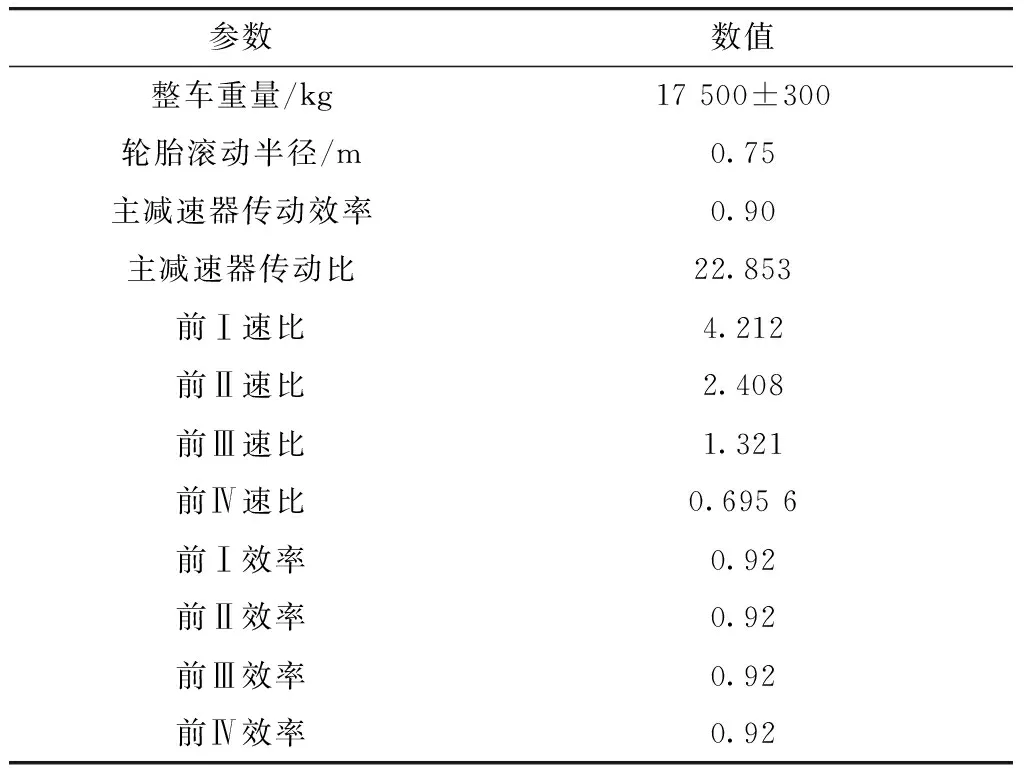
表1 整车参数

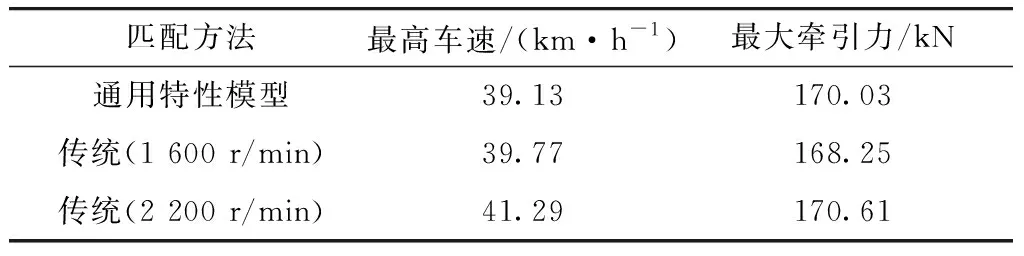
表2 最高车速以及最大牵引力Tab.2 Maximum speed and peak traction

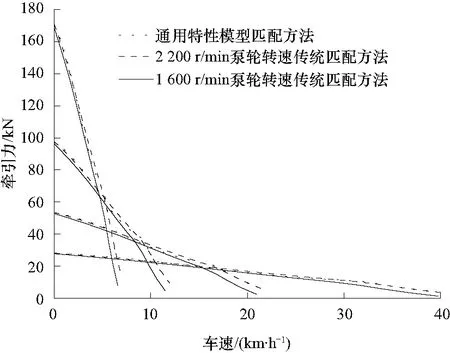
图13 不同匹配方法下装载机牵引力特性Fig.13 Traction characteristics of loader under different matching methods

5 结 论

本文考虑了液力变矩器泵轮转速对其特性的影响，利用BP神经网络对液力变矩器的通用特性进行研究，并结合发动机转速-转矩特性提出了液力变矩器通用特性与发动机的匹配方法.

对某液力变矩器进行不同泵轮转速下稳态特性试验.利用传统方法进行不同泵轮转速下的发动机与液力变矩器特性匹配后，发现泵轮转速对匹配结果影响较大，特别在高速比工况下，匹配误差呈现指数增长的趋势.根据有限的液力变矩器稳态特性数据，利用BP神经网络构建液力变矩器通用特性预测模型，确定了BP神经网络结构及隐含层节点数，结果表明模型预测误差均值在3%以内，与传统的经验公式修正方法相比预测精度有较大提升，因此神经网络模型实现了不同泵轮转速工况下液力变矩器转矩特性的准确预测.

利用离散化涡轮的方法将共同输入特性交线的问题转换为二分法求取系列交点问题，构建了发动机与液力变矩器通用特性的匹配模型，该模型考虑了泵轮转速对液力变矩器特性的影响，能够更准确的反映发动机与液力变矩器共同工作的实际情况，提高了匹配精度和实际装载机牵引力特性的预测精度.对于性能随着泵轮转速具有强线性变化趋势的液力变矩器，可采用较少泵轮转速样本点采集实验数据；对于性能随泵轮转速有较强非线性变化趋势的液力特性的液力变矩器，应采用更多的泵轮转速样本点来采集实验数据，进而提高匹配模型的预测精度.