基于仿真的选区激光熔化工艺结构变形补偿 设计优化

刘检华，任策，夏焕雄，敖晓辉，林圣享 (北京理工大学 机械与车辆学院，北京 100081)

选区激光熔化工艺是增材制造的重要技术之一，其通过高能激光束选择性地熔化和融合金属粉末来构建高致密度的3D零件，由于其成型精度高、成型零件几何结构复杂的特点已经被广泛运用到航空航天、机械电子以及医疗等领域[1].螺旋桨结构是广泛应用于航空、船舶等领域的重要零件结构，其兼具曲面结构与薄壁结构的典型特点.曲面结构的特点是几何较为复杂，使得有支撑条件下的零件后处理比较困难，而无支撑条件下成型缺陷较多；金属薄壁结构的特殊性使得零件在一个方向上尺寸较小，在加工过程中温度梯度变化更为剧烈，冷却后将产生较大的残余应力及变形，最终导致成型后的尺寸与期望尺寸误差较大.因此，有效遏制残余应力导致的零件变形是该工艺亟待解决的重要问题[2].

由于SLM工艺的复杂性以及试验检测的高成本，数值模拟研究方法被广泛应用于SLM成型工艺规律的研究、工艺参数的探索以及零件结构的设计等.其中，SLM成型过程中的传热与变形问题是研究的关键问题，国内外学者基于数值模拟方法对SLM过程中热-变形耦合问题做了一系列研究.柯林达等[3]探究了激光扫描速率和铺粉层厚对SLM成型钛合金薄壁件应力演变的影响规律，同时模拟了去应力退火过程，发现应力演变呈现周期性变化；Duan等[4]使用自适应网格方法进行了空心圆柱形状零件的SLM温度场模拟，结果显示零件内部温度明显高于外部温度；Luo[5]将SLM工艺数值仿真中的移动高斯点热源用点-线混合热源代替作为能量输入，在兼顾求解精度的前提下大大提高了模拟效率；倪辰旖[6]基于固有应变法对SLM成型过程建立了一种“热源-局部-结构件”三级递进模型，并通过了实验验证；Li等[7]采用基于温度场和基于应力场的两种方法对薄壁零件的残余应力和变形进行了快速预测，并与实验结果进行了对比，结果表明温度场方法较应力场方法对变形的预测更符合实验测试.

在SLM成型零件的残余应力及变形的优化研究方面，Parry[8]基于数值模拟优化了激光扫描线的长度范围以及旋转方向等因素，在Ti6Al4V合金成型过程中获得了最佳的应力分布状态；Promoppatum[9]建立了SLM热-力耦合数值模型，探究了宏观尺度桥结构的激光功率、扫描线长等工艺参数对残余应力形成的影响规律并进行实验测量验证，得出了使残余应力大大减小的最佳工艺参数；Yaghi等[10]采用有限元方法模拟了叶轮的SLM加工过程中的变形和残余应力，然后在数值模拟过程中利用有限元计算的变形场进行反向变形补偿，实现了叶片相对期望几何结构的变形量的降低.

针对SLM成型螺旋桨结构叶片容易产生较大的残余应力导致的变形问题，本文介绍了一种基于有限元热-力耦合仿真的结构变形补偿设计优化方法.该方法通过构建适当的变形场反馈迭代，自动调整螺旋桨几何结构，可实现成型后的结构与期望结构之间的几何误差逐步减小，直到满足设计要求.

1 基于有限元方法的热-力耦合仿真与变形补偿方法

基于仿真的变形补偿方法的总体流程如图1所示，主要包含SLM工艺构件热-力耦合仿真以及变形场补偿方法两个环节，其具体流程是：首先建立具有期望几何的构件的有限元分析模型，并定义相应的物性参数与边界条件，在ABAQUS软件中将几何模型分层，而后生成铺粉过程和激光移动的事件序列文件，提交分析计算后得到构件的温度场、应力场以及变形场；将变形后的几何与期望几何做比较，若最大变形量不满足设计精度要求，则将几何表面所有节点的坐标施加反向变形补偿，生成新的几何模型及其激光扫描轨迹，并重新定义铺粉过程和激光移动的事件序列文件，进行下一次迭代的有限元仿真，直到最后一次变形补偿后的仿真得到的几何相较于期望几何的最大变形量满足设计精度要求则输出优化的几何结构.

1.1 数值模型的建立

SLM工艺是将金属粉末材料熔化、并逐层堆积形成致密实体的过程，金属粉末在极短的时间尺度内经历多种状态变化，其材料属性也随之改变.采用ABAQUS实现SLM工艺仿真中的激光能量按预设时空坐标输入以及单元按预定时间逐线-逐层激活.其中热分析采用瞬态传热模型，应力分析采用准静态模型.为反映金属粉末在SLM工艺过程中获得的能量输入及其材料属性的变化，采用用户子程序(UMDFLUX)定义激光的能量输入，同时，采用用户子程序(UEPACTIVATIONVOL)定义移动热源和材料沉积的事件序列信息.

对于SLM过程，每层铺粉厚度大约在0.1 mm左右，相较于构件的整体高度非常小，使得需要沉积的层数很多，一般地对于dm数量级高度的构件，需要的沉积层数大约在1 000层左右，为了提高宏观结构件的仿真计算效率，通常采用一层网格表示多层铺粉过程[11].

本文研究的螺旋桨模型的几何尺寸如图2所示.整个有限元分析模型由两部分构成：螺旋桨结构和基板.螺旋桨整体高度为45 mm，由同一截面螺旋扫掠而成，中间是直径为18 mm的圆柱，周围有4个厚度为4 mm的叶片，整个截面从底部到顶部共转过90°.在数值模拟中，将整个螺旋桨结构沿高度方向分为90层，打印过程中从下而上逐层激活，有限元瞬态热分析使用六面体单元对分层的构件进行网格划分，单元类型为DC3D8.有限元准静态应力分析使用的单元类型为C3D8R；基板结构使用规则的六面体网格.整个模型的网格数量为565 953，整个打印过程持续时间为5 625 s.

图2 螺旋桨模型的几何尺寸Fig.2 Dimension of the propeller model

1.1.1SLM构件传热数值模型

激光扫掠过程中，能量只有小部分被金属粉末吸收并熔化、凝固形成实体，大部分激光能量由于反射而损失；受热的实体会与周围金属粉末产生热传导，此处传热导造成的热量损失采用对流换热等效；激光工作的顶层温度较高，此处考虑热量的辐射损失.因此，SLM构件热传分析包含能量吸收、热传导、热对流、热辐射，其示意图如图3所示.

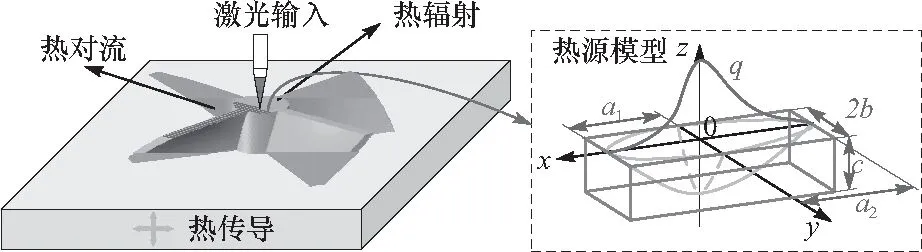
图3 SLM成型过程中能量传递示意图及热源模型示意图Fig.3 A schematic of heat transfer and the heat source model during the SLM process

传热分析中SLM构件被视为均匀、连续的各向同性固体材料，其瞬态传热过程的控制方程可表示为

Q(x,t)

(1)

式中:cp为比热容;k为热传导系数;ρ为材料密度;Q为能量源项;ΔH为相变潜热;β为熔化/凝固率,β=(T-Ts)/(Tl-Ts).其中cp和k考虑随温度变化.

考虑能量吸收、热对流和热辐射的边界条件可表示为

(2)

式中:n为表面法线方向;h为热对流系数，取18 W/(m2·K);σ为玻尔兹曼常数，取5.67×10-8W/(m2·K4);ε热辐射系数，取0.45.所有单元的初始温度为环境温度,T0=300 K.

针对激光能量输入选择深度方向指数衰减的双椭球体热源模型，其示意图如图3所示，激光的输入在有限元分析中以热流密度的形式施加在单元体上.双椭球体热源模型由前后各1/4的椭球构成，双椭球体热源模型的表达式为

(3)

式中:a1、a2、b、c为相互独立的热源参数;η为激光吸收率，文中取η=0.34;P为激光功率;ff、fr分别为前后椭球的能量分数，满足ff+fr=2.

数值仿真过程中的激光扫描相关参数如表1所示.

表1 加工过程中的扫描参数[12]

1.1.2SLM应力场数值模型

在SLM工艺过程中，温度的剧烈变化会造成零件内部的应力分布不均匀，以及金属粉末的熔化和凝固形成残余应力，并最终导致残余变形.一般情况下，SLM工艺过程中热应力导致的变形量相较于构件尺寸是小量，可认为应变位移对热传递的影响可以忽略不计，因此，SLM宏观尺度的热-力耦合问题可采用温度-应力单向耦合简化.在有限元热-力耦合分析中，首先通过瞬态传热分析计算出成型过程中的温度场之后，将其产生的热应变引入准静态应力分析模型.

准静态应力分析中的总应变包含弹性应变、塑性应变及热应变,即

ε=εe+εp+εT

(4)

其中，εe为弹性应变张量，由如下本构关系确定：

{σ}=[D]{εe}

(5)

式中:σ为应力张量;D为刚度矩阵;εp为塑性应变，由材料屈服曲线确定;εT为温度引起的各向同性热应变，可用材料的线膨胀系数αT对温度T的积分计算：

(6)

本文SLM工艺使用的材料为AlSi10Mg，其比热容、热传导系数、杨氏模量以及线膨胀系数随温度变化数据曲线如图4所示，其他物性参数如表2所示.

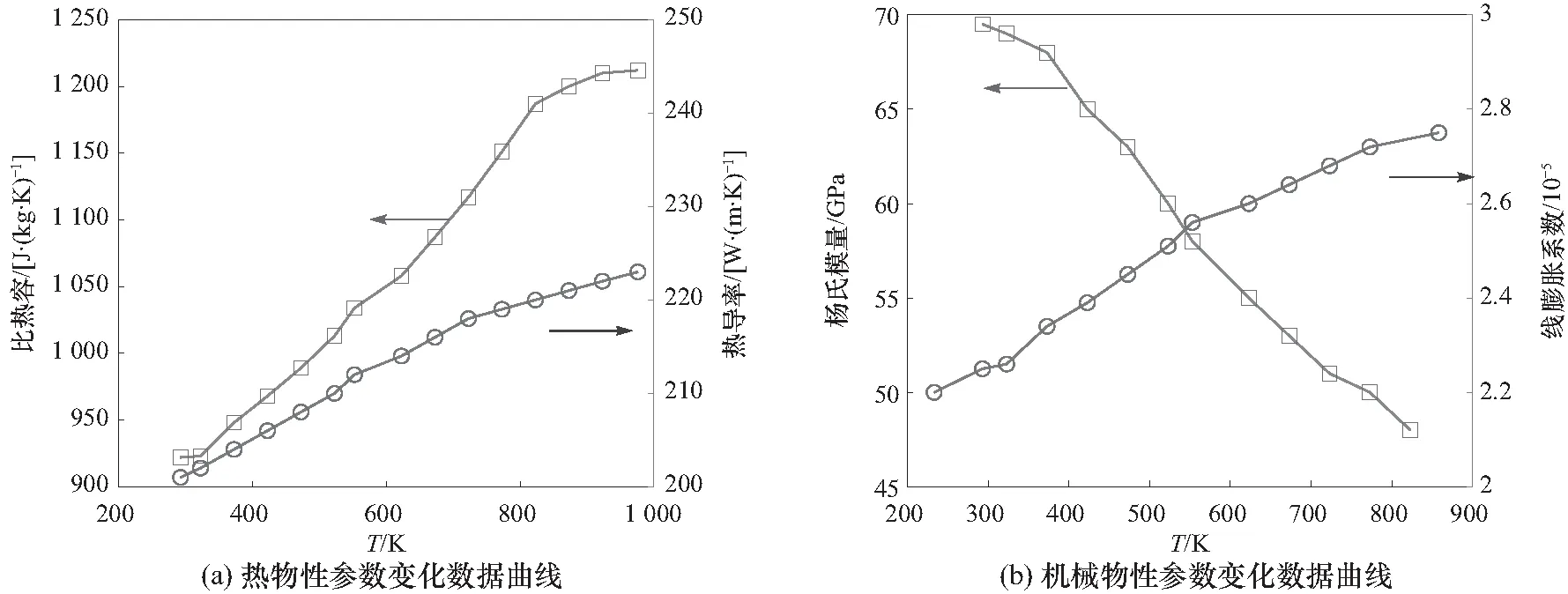
图4 AlSi10Mg随温度变化的热物性参数与机械物性参数Fig.4 Temperature-dependent thermal properties and mechanical properties of AlSi10Mg

表2 AlSi10Mg不随温度变化的材料属性

1.2 变形补偿方法

在第一次变形补偿之前，首先获取期望几何模型经有限元仿真计算得到的变形后的所有节点坐标，图5(a)所示为第一次成型后得到的变形几何模型的网格.通过Matlab读取变形后的几何模型的节点数据，而后与期望几何模型的节点数据进行比较，得到相较于期望模型的变形场. 再根据此变形场进行补偿，生成新的几何模型，如图5(b)所示.如此不断迭代，直至仿真计算得到的变形后的几何结构与期望几何之间的误差满足设计要求.文中设计的变形场补偿算法为比例反馈调节算法，表示为

图5 期望几何模型成型后的变形几何以及变形补偿后的几何模型示意图Fig.5 The finished part obtained from the desired geometry and the designed geometry by deformation compensation

(7)

式中:Ci为设计的几何模型的节点坐标;Ai为仿真计算得到的变形几何的节点坐标;Pi为期望几何的节点坐标;λ(0<λ<1)为补偿因子.该变形场补偿算法的收敛条件为

‖Ai-Pi‖max≤ε

(8)

另外，由于待打印的几何模型产生了变化，原先的激光路径轨迹不再精确，因此需要对新的几何模型重新构建铺粉过程和激光移动的事件序列信息.

2 结果分析与讨论

2.1 应力结果与讨论

图6为期望几何模型有限元仿真后的应力在模型表面及中间截面上的分布云图.零件经过打印过程和冷却过程之后最大应力约为228 MPa，位置在螺旋桨结构的第一层，圆柱区域的边缘位置.圆柱区域内部的残余应力呈现边缘大中间小、底部大顶部小的分布特征.该特征与构件成型过程中的散热特征基本一致：边缘对流散热作用强烈,底部与低温基板传导散热强烈导致降温快、残余应力高，随高度增加热量逐渐积累,散热速率下降使得降温慢、残余应力低.在距离螺旋桨顶部平面5.52 mm的位置出现了一个明显的残余应力较小的区域，该区域内的应力在30～45 MPa范围，由散热特征分析可知，该区域是打印完毕后螺旋桨整体冷却过程中温度最高的区域.另外，对观察叶片表面的残余应力分布发现，相较于叶片上表面，叶片的下表面残余应力更为明显.

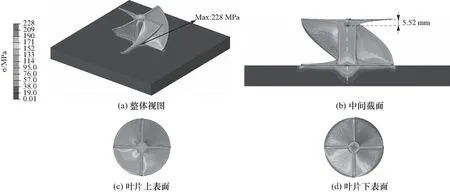
图6 期望几何模型成型后的残余应力分布Fig.6 The distribution of residual stress in the finished part from the desired geometry

2.2 变形结果与讨论

图7所示为期望几何模型有限元仿真后的位移在模型表面及中间截面上的分布云图.从图中可以看出，零件的最大变形发生在螺旋桨结构的4个叶片的边缘，且位于中间偏上的位置，最大变形量达1.69 mm，叶片可见明显的向上翘曲现象，其顶部已不处于同一平面.同时，在螺旋桨结构内部的变形分布呈现中间变形大而靠近顶部和底部的区域变形小，这是由于冷却收缩所致.

图7 期望几何模型成型后的位移分布Fig.7 The displacement distribution in the finished part from the desired geometry

取叶片边缘特征线MN(如图7所标记)，此特征线上的变形量随高度变化曲线如图8所示.从图中可以看出，叶片边缘变形量随沉积高度的增加，先变大后减小，变形量在29.3 mm高度处达到最大1.69 mm，而后变形逐渐减小，在叶片顶端变形1.31 mm.

图8 叶片边缘变形量随高度的变化曲线Fig.8 Deformation along the height at the edge of the blade

由于初始的期望几何模型成型后形变量较大，对其实施变形场补偿. 图9所示经过4次变形场补偿迭代得到的新几何模型成型后的变形云图以及最大残余应力，需要注意的是该变形云图是相对各自迭代步的设计几何模型，而不是相对于期望几何模型的变形.从4次迭代可以看出，相较于各自设计几何模型的变形分布以及最大残余应力并无明显差别.最大变形均在叶片边缘附近，大约1.7～1.8 mm；最大应力均在中间圆柱区域的第一层边缘附近，其值227～228 MPa.

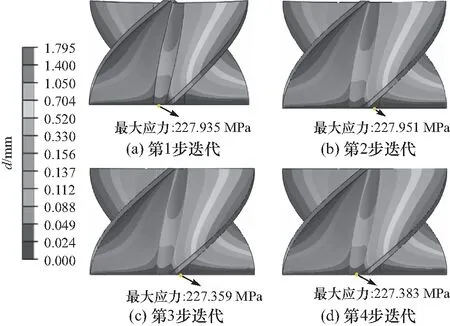
图9 四次变形补偿迭代的变形云图及最大应力分布示意图Fig.9 Deformation contours and maximum residual stresses in the four deformation compensation iterations

将上述4次变形场补偿迭代得到的成型后的螺旋桨结构与期望几何结构相比较，得到的变形场云图如图10所示.由云图可知，成型后得到的几何相较于期望几何的变形量显著减小，经过四次变形场补偿之后，最大变形量由1.690 mm减小到0.087 9 mm.由变形量的收敛过程可知，根据此变形迭代方法，当迭代步数足够多，最终的最大变形将会逐渐趋于0，此时成型得到的模型即为期望几何模型.

图10 成型仿真得到的最大变形随变形补偿迭代次数的变化Fig.10 The maximum deformation changes with the deformation compensation iterations

3 结束语

SLM工艺成型螺旋桨结构残余应力分布特征与降温特征相一致，降温快的位置残余应力大；最大应力发生在中间圆柱的底层边缘位置，最小应力在距离中间圆柱内部距离顶部5.52 mm的位置；螺旋桨叶片下表面相较于上表面残余应力更大，残余应力影响的区域也更大.螺旋桨结构竖直成型时，螺旋桨叶片的变形较大，且最大变形量发生在叶片边缘中间偏上的位置.经过四次变形场补偿迭代，螺旋桨构件最大变形由最初的1.69 mm降低至0.087 9 mm，减小了94.8%，从仿真的角度验证了变形场补偿方法优化SLM成型结构设计的有效性.