木材节子图像增强的小波变换与双三次插值融合方法
秦彦平,张 军,多化琼*,贺春光,高 凡
(1.内蒙古农业大学 材料科学与艺术设计学院,内蒙古 呼和浩特 010018;2.内蒙古农业大学 理学院,内蒙古 呼和浩特 010018)
图像增强是指通过一些技术手段改善图像质量,从而提高图像视觉效果,将原来不清晰的图像变得清晰或者突出图像的某些应用特征,便于对图像进一步的处理和研究[1]。随着数字图像处理技术的迅速发展,图像增强技术逐步应用到人类生产和生活的各个方面,新的图像增强方法不断涌现。为了解决图像处理过程中颜色失真、对比度下降、边缘细节不明显等问题,王延年等[2]在人工蜂群优化算法确定最优灰度变换曲线的基础上,设计出一种提高图像对比度的自适应增强算法。李毅等[3]基于人眼视觉掩盖效应,提出一种尺度变化高斯核平滑滤波的Retinex红外图像增强算法。胡俊等[4]基于卷积神经网络提出了激光图像增强算法。陆涛[5]基于统计特征分类耦合自适应Gamma校正,构造出一种提高视觉效果的图像增强算法。肖创柏等[6]基于引导滤波Retinex提出一种快速夜间彩色图像增强算法。崇元等[7]基于局部梯度极值点,提出了改进的BEMD图像增强方法。周浦城等[8]基于卷积分析稀疏表示和相位一致性,设计了低照度图像增强方法。陶志勇等[9]基于改进天牛须群优化算法提出了低照度纹理图像增强方法。黄果等[10]提出了一种基于非局部多尺度分数阶微分图像增强算子。
树节是树木生长的正常生理现象,往往存在于树干内部以及枝条的基部,在用材中被称为木材节子[11]。木材节子是木材质量等级判定的重要依据,它不仅影响木材表面的美观程度,而且还会影响木材的力学性能[11]。马坤等[12]为了增强木材图像的对比度,提出了一种小波变换和傅里叶变换相融合的木材图像增强方法。袁云梅等[13]为了提高木材图像的识别率,提出了一种基于权重系数的木材图像增强方法。因此,作为提高木材节子识别率重要手段之一的图像增强技术对木材加工与有效利用具有重要意义。小波变换可以将图像信号分解为代表图像整体特征的低频分量和代表图像边缘细节的高频分量,双三次插值算法能使图像在变换过程中边缘更加平滑、细节质量保留更加完好[14]。然而,小波变换处理图像的难点在于选择合适的小波基函数小波分解尺度,为了提高木材节子图像的清晰度和对比度,使其轮廓清晰对比分明,本研究提出一种基于Haar小波基函数的单尺度小波变换与双三次插值融合的木材节子图像增强方法。
1 材料与方法
1.1 材料
木节是指包被在树干中的枝条基部[15]。根据木节与树干的连生程度,木节分为活节和死节。由活枝条形成的与周围正常木材组织紧密连生构造正常的木节称为活节,其形状大多数为圆形和椭圆形,周围边界变化缓慢且具有渐变性;由枯死枝条形成的与周围正常木材组织脱离或部分脱离的木节称为死节,其形状大多数呈圆形和椭圆形,与周围正常木材组织之间具有明显的边界[16]。
使用照相机三脚架和索尼DSC-W830便携数码照相机在自然光条件下采集木材节子图像,为了便于进行图像增强,将原图像设置为128×128像素的图片,保存为PNG格式,以活节(图1a)和死节(图1b)图像为研究对象,在Windows10操作系统,内存为8GB的计算机中采用MATLAB R2017b进行编程计算和仿真试验。

图1 木材节子图像Fig.1 Images of living (a) and dead wood (b) knots
1.2 理论
本研究提出的小波变换与双三次插值融合的图像增强方法的理论主要包括二维离散平稳小波变换、二维提升小波变换和双三次插值法。
1.2.1 二维离散平稳小波变换 二维离散平稳小波变换是一种将信号进行压缩和分解的频域处理技术,因其具有局部时频特性、频率压缩以及多分辨率特性,使得其在图像处理方面被广泛应用[17]。二维离散平稳小波变换的基本思想和原理[18-20]是对每一层的数据应用适当的高、低通滤波器,在下一层产生2个长度都与原始序列相同的新序列,大小为M×N的图像f(x,y)的离散小波变换是:
(1)
式中,φj,m,n(x,y)=2j/2φ(2jx-m,2jy-n)为尺度函数。
(2)

1.2.2 二维提升小波变换 二维提升小波变换的基本思想是将图像分解成不同频率的子图像并进行相应的平滑处理,具体包括3个阶段:分裂、预测、更新[21]。
第1阶段:分裂,即将原始图像分成高频细节子带和低频细节子带。Split(aj):=(aj-1,bj-1),其中,aj-1表示低频子带,bj-1表示高频子带,符号“:=”表示对变量的更新而不是一个等式。
第2阶段:预测,即将原始的纹样分为偶数系列和奇数系列,利用2个系列的相关性,由偶数系列来预测奇数系列。bj-1:=bj-1-p(aj-1),其中,p为预测函数。
第3阶段:更新,即经过分裂产生的子带的特征可能与原纹样不一致,为了保持原纹样的特征,需要进行更新,以此来减少差异。aj-1:=aj-1+U(bj-1),其中,U表示更新过程,U(bj-1)为更新后的子带。
2.2.3 双三次插值法 双三次插值是在二维空间图像中“插值”或增加“像素”数量的方法,通常运用在图像处理中,对原图像进行放大或缩小。该方法利用多项式S(x)来逼近理论上的最佳插值函数sinx/x,其公式[22]为:
(3)
式中,|x|是周围像素沿x方向离原点的距离。
待求像素(x,y)的灰度值计算公式为:
f(x,y)=f(i+n,j+m)=MNQ
(4)
式中,m,n分别是待求像素与原像素(i,j)在x,y方向上的距离,

(5)
1.3 技术流程
采用二维离散平稳小波变换(stationary wavelet transform,SWT)和二维提升小波变换(lifting wavelet transform,LWT)将原图像进行二维分解,分解为高高(HH)、高低(HL)、低高(LH)和低低(LL)3个高频子带和1个低频子带。对二维提升小波变换中的3个高频子带和1个低频子带进行双三次插值,然后将插值后的3个高频子带与二维离散平稳小波变换得到的3个高频子带叠加,得到新的高频子带,对新的高频子带与二维提升小波变换插值后得到的低频子带进行逆提升小波变换(inverse lifting wavelet transform,ILWT),得到最终的高对比度图像(图2)。

图2 技术流程Fig.2 Technical flow chart
2 结果与分析
将木材节子的彩色图像转换为灰度图像(图3)。活节和死节的灰度图像分别经过二维离散平稳小波变换和二维提升小波变换所得子带图像(图4和图5)。对基于二维提升小波变换所得子带图像LL2、LH2、HL2、HH2进行双三次插值后得到的子带图像LL3、LH3、HL3、HH3(图6、图7)。

图3 木材节子彩色图像与灰度图像Fig.3 Color images and gray images of wood knots

图4 活节图像变换后的高、低频子带图像Fig.4 High and low frequency subband images of living knot after transformation

图5 死节图像变换后的高、低频子带图像Fig.5 High and low frequency subband images of dead knot after transformation

图6 活节图像经二维提升小波变换和双三次插值后的高、低频子带图像Fig.6 High and low frequency subband images of living knot after two dimensional lifting wavelet transformation and bicubic interpolation

图7 死节图像经二维提升小波变换和双三次插值后的高、低频子带图像Fig.7 High and low frequency subband images of dead knot after two dimensional lifting wavelet transformation and bicubic interpolation
对上述基于二维离散平稳小波变换得到的高频子带LH1、HL1、HH1与对基于二维提升小波变换后进行双三次插值得到的高频子带LH3、HL3、HH3叠加得到新的高频子带图像LH、HL、HH(图8、图9)。

图8 活节的新高频子带图像Fig.8 The new high frequency subband images of living knot

图9 死节的新高频子带图像Fig.9 The new high frequency subband images of dead knot
对上述新的高频子带与基于二维提升小波变换后做双三次插值得到的低频子带LL3进行逆提升小波变换,得到新的高对比度灰度图像和增强后的高对比度彩色图像(图10)。

图10 增强后的木材节子灰度图像与彩色图像Fig.10 Enhancement gray and color images of wood knots
2.1 主观评价
将本方法与传统的直方图均衡化和双三次插值法进行对比,对木材节子图像的处理结果如下。
图11b和图12b相对于其他图像来说颜色“过亮”,节子图像不清晰。这是由于直方图均衡化方法会将原始图像的直方图变换为均匀分布的形式,导致了变换后图像的灰度级减少,部分细节消失。图11c和图12c采用的是双三次插值方法,与其他图像相比,颜色相差较大,失真严重,且纹路粗糙、节子轮廓边缘模糊。图11d和图12d采用的是本研究提出的图像增强方法,亮度适中,颜色失真小,图像质量好,且与原图像相似程度最高,与前2种方法的处理结果相比,保留了更多的原图细节信息。

图11 活节原图像与3种算法重构后的图像Fig.11 Original image and images transformed by three algorithms of living knots

图12 死节原图像与3种算法重构后的图像Fig.12 Original image and images transformed by three algorithms of dead knot
2.2 客观评价
主观评价结果易受观察人视觉差异的影响,为更加科学合理地评价图像增强效果,需要进一步使用客观评价指标来衡量增强后图像的质量和图像处理技术的有效性。本研究将峰值信噪比(peak signal to noise ratio,PSNR)、结构相似性指数(structural similarity index,SSIM)和平滑指数(filter index,FI)作为客观评价指标,对提出的小波变换与双三次插值融合的图像增强方法与传统的直方图均衡化和双三次插值方法的结果进行比较。
1)峰值信噪比(PSNR)[23]可以反映增强后图像的失真性,其值越大表示失真越小,增强效果越好。PSNR的计算公式如下:
(6)
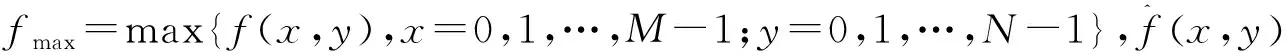
从表1可以看出,3种算法处理后,活节图像的PSNR值分别为17.668 7、19.382 5 dB和22.994 8 dB;在死节图像的增强效果上,3种增强方法的PSNR值分别为13.859 6、15.089 1 dB和32.054 1 dB,由此可知使用本方法重构的木材节子图像的PSNR值相较于直方图均衡化和双三次插值法都有一定的提高,说明重构的图像去噪效果良好,增强图像的对比度有所提高,图像增强效果显著。

表1 3种图像增强方法重构的木材节子图像的PSNR值Table 1 PSNR values of wood knob images reconstructed by three image enhancement methods
2)结构相似性指数(SSIM)[24-25]可以衡量重构后图像与原木材节子图像的相似程度,其值越大表示相似程度越高,SSIM的计算公式如下:
(6)
式中,C1=(μ1L)2,C2=(μ2L)2,μ1=0.01,μ2=0.03,L=255,C3=C2/2,ρx表示图像x的均值,ρy表示图像y的均值,φx表示图像x的标准差,φy表示图像y的标准差,φxy表示图像x与图像y的协方差。
从表2可以看出,3种算法处理后,活节图像的SSIM值分别为0.714 9、0.613 7和0.928 9;在死节图像的增强效果上,3种增强方法的SSIM值分别为0.634 9、0.591 3和0.919 2,由此可知使用本方法重构的木材节子图像的SSIM值相较于直方图均衡化和双三次插值法有大幅度的提高。说明本方法重构的图像与原图像相似程度较高,增强图像质量较好。

表2 3种图像增强方法重构的木材节子图像的SSIM值Table 2 SSIM values of wood knob images reconstructed by three image enhancement methods
3)平滑指数(FI)[26]是指增强后图像像元的均值与其标准差的比值,它可以反映算法对噪声的平滑能力,FI的计算公式为:
(7)
式中,残差e=|FI增强后图像-FI原图像|。
从表3可以看出,3种算法处理后,重构的活节图像的FI值与原图像的FI值之差分别为1.389 1、0.185 9和0.183 9;在死节图像的增强上,3种增强方法重构后死节图像的FI值与原图像的FI值之差分别为2.196 4、1.383 8和0.026 1。显然,本方法重构的木材节子图像的FI值与原图像的FI值之差最小。这说明本方法不仅可以有效平滑噪声,而且细节保留较为完整。

表3 原图像与3种图像增强方法重构的木材节子图像的FI值Table 3 FI values of wood knob original images and images reconstructed by three image enhancement methods
3 结论
基于木材节子图像的边缘特征,考虑到小波变换能把图像分解为低频分量(代表图像整体特征)和高频分量(代表图像细节特征),双三次插值能使图像在变换过程中细节质量保留更加完好的技术特性,本研究提出小波变换与双三次插值融合的木材节子图像增强方法,并将此方法与传统的直方图均衡化和双三次插值方法进行对比。从主观评价结果来看,本方法处理后的图像颜色失真小,图像质量好,优于2种传统的图像增强方法。从客观评价结果来看,本方法处理后的活节和死节图像在峰值信噪比、结构相似性指数和平滑指数分别为22.994 8、32.054 1,0.928 9、0.919 2,2.934 2、3.889 3,均优于2种传统的图像增强方法,这进一步表明本方法具有较好的去除噪声效果和保留细节性能。

