混凝土连续箱梁高宽比对竖向挠度的影响

原在兴

(中铁十八局集团建筑安装工程有限公司，贵州安顺 561000)

随着我国交通建设的不断发展，以及国家“十三五”规划布局实施，为了响应国家提出“新基建”的建设理念，宝鸡至兰州的客运专线穿越秦岭山脉的河谷地段采用混凝土薄壁连续箱梁，混凝土薄壁连续箱梁由于自重轻，跨越能力强和结抗弯和抗扭刚度大的特点，其广泛应用，优势明显[1-4]。焦海平利用最小势能原理推导了一种能快速计算箱梁剪滞与剪切双重效应的挠曲微分方程，与有限元结果对比，证明了解析解的合理性[5-6]；蔺鹏臻从弯曲曲率方程角度出发，分析了剪力滞对箱梁挠度的影响，提出了一种箱梁考虑剪力滞的有效翼缘分布宽度的修正方法[7]；R.Eeissner在上个世纪应用变分法的最小势能原理推导了箱梁剪力滞效应的微分方程，并且假定其应引起翼板的纵向位移差函数u(x,y)沿横向按二次抛物线变化[8-9]。由于连续箱梁跨度大，为了分析不同宽跨比条件下箱梁考虑剪力滞效应后的竖向挠度，我国现行的铁路桥梁设计规范提出特定边界条件的梁承受荷载作用的最大挠度的限值[10]，根据规范对挠度的限值，探讨桥梁安全前提下，满足经济性和适用性条件下箱梁最优宽跨比的设计取值。

1 叠加原理

混凝土连续梁由于截面抗弯和抗扭刚度大，箱梁成桥后本身为超静定受理体系，往往采用对称等跨的结构形式达到力系平衡的目的，中跨支座通常采用刚接的约束条件，边跨采用铰接的方式，中跨支座处一般采用刚结形式，该节点左右采用等跨结构，支座处能有效抵消支点处负弯矩和边跨传递到该处的正弯矩，一方面减小支座处的最大Mmax，另一方面保证了施工及正常运营中的结构稳定性。为了简化计算，K.R与P.J曾提出采用叠加原理求解具有超静定结构力系的连续梁的对处于线弹性变形阶段的连续箱梁剪力滞效应[11]，由于连续箱梁沿纵向的变形仍满足一般边界条件的限定。如图1所示，即假定箱梁正应力沿箱梁横截面按二次抛物线形式分布，因此文献[11]计算混凝土连续箱梁在剪滞效应的竖向变形是单个基本受力体系叠加效果，即承受荷载作用下的混凝土连续箱梁整体为基本单个静定体系的内力σi与剪滞系数λi的乘积与截面的超静定内力σi的比值，公式(1)、(2)为叠加原理公式。

图1 横截面弯曲正应力分布

(1)

(2)

式中：M—计算截面处超静定体系的弯矩(单位：kN·m)；Mi—承受单一作用下的基本体系计算截面处弯矩(单位：kN·m)；W—计算截面的抗弯模量(单位：m3)；λ—在计算截面处的超静定结构的剪力滞系数，比值为箱梁考虑剪力滞效应与Euler-Bernoulli梁理论的横截面正应力比值；λi—承受单一作用下的基本组成体系的剪力滞系数，超静定结构在计算截面处的剪力滞系数，比 值为箱梁考虑剪力滞效应与Euler-Bernoulli梁理论的横截面正应力比。

与Euler-Bernoulli梁理论相比，箱梁考虑剪力滞效应后产生竖向附加挠度Mf。宽箱型截面由于较大的肋板间距往往发生平面内弯曲，上、下翼缘板由于收到其剪切变形沿肋板传递中不一致的影响，其平面内弯曲变形不再符合Euler-Bernoulli的平截面假定，即原来的广义位移方程无法准确表示其挠曲变形，因此R.Eeissner根据最小势能原理引入上、下顶板的最大剪切变形差函数u(x,y)，如公式(3)和(4)。

w=w(x)

(3)

(4)

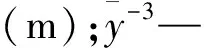
2 有限元模型构建与分析

为了准确分析横截面高宽比变化引起的连续箱梁竖向挠曲分布情况，利用通用有限元分析软件ANSYS建立宝兰客专某双跨连续箱梁，采用C40浇筑，全长L=30+30m，支座边界为端铰接，中间刚结点，桥面宽11m，上下翼缘板和肋板厚度0.25m，梁宽11.0m，截面高宽比介于0.25～0.35，参数取值如表1所示。solid45单元用于构造三维实体结构，通过8个节点来定义模拟的实体，因为每个节点有3个沿着x、y、z方向平移的自由度，具有塑性、蠕变,膨胀、应力强化、大变形和大应变能力的特点，因此选择8节点单元solid45，单元的坐标系如图2所示，计算断面和有限元数值模型如图3、4所示。

图2 solid45单元的坐标系

图3 计算断面

表1 计算参数

图4 30+30m连续箱梁的数值模型(m)

由图5可见，连续箱梁承受相同的荷载作用下，随着横截面的高宽比逐渐增大，h/b介于0.25～0.35时，h/b=0.25，最大挠度为3.98mm；h/b=0.30，最大挠度为3.05mm；h/b=0.35，最大挠度为1.70mm。随着高宽比的增加，跨中最大挠度逐渐减小，不同h/b对考虑剪力滞效应后混凝土连续梁的挠度与h/b呈近似反比关系。h/b=0.25～0.30，高宽比增大20%，竖向挠度减小23.6%；h/b=0.30～0.35，高宽比增大17%，竖向挠度减小44.3.%，后者高宽比增大引起挠度增大是前置的1.9倍，高宽比的增大对竖向挠度的影响明显。

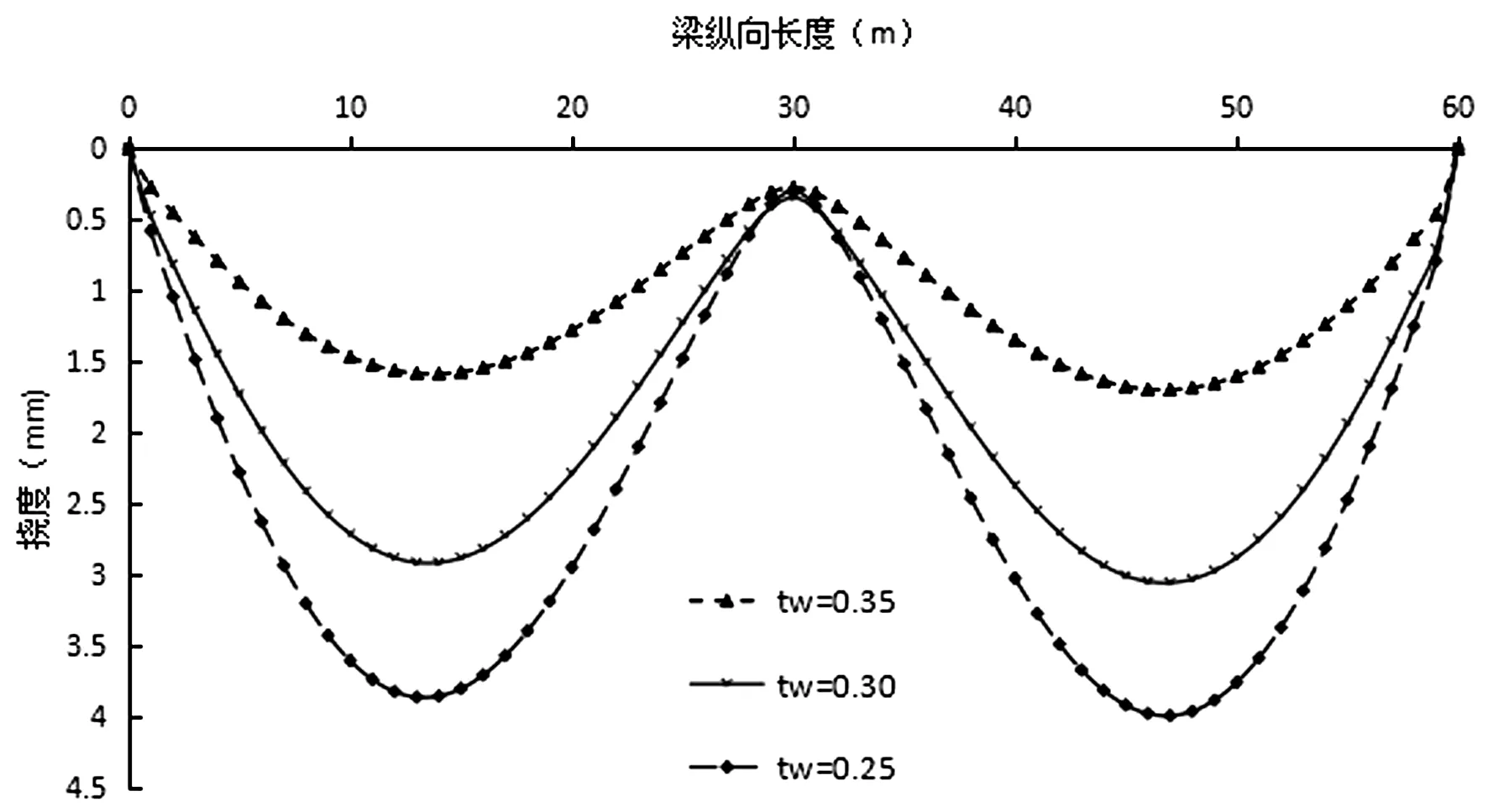
图5 连续梁竖向挠度分布(mm)

3 结 论

本文从宝兰客专的某混凝土连续箱梁为算例，为了研究截面h/b变化对考虑箱梁剪力滞效应下竖向挠度的影响，建立有限元模型，主要结论如下：

(1) 对比分析了不同截面高宽比条件下考虑剪力滞效应连续箱梁的竖向挠曲分布特征，随着截面h/b从0.25变化至0.35，竖向挠度也从3.98mm至1.70mm，随着高宽比的增加，跨中最大挠度逐渐减小，不同h/b对考虑剪力滞效应后混凝土连续梁的挠度与h/b呈近似反比关系。

(2)我国规范规定大跨度箱梁采用限制高宽比来控制剪力滞效应引起附加挠度的影响，这一做法偏于单一、保守的，本文研究成果在今后保证桥梁安全、经济性和适用性条件下，随着截面高宽比从小变大，箱梁的挠度逐渐明显减小，因此箱梁最优宽跨比可以取较大值，如高宽比=0.25～0.30。在设计取值中，可适当的增大高宽比达到经济、适用的目的。