数形结合思想在初中数学教学中的渗透路径研究

王宁宁

摘要：初中数学可以锻炼学生的逻辑思维能力、空间想象能力以及运算能力，是集思想、知识、能力教育于一体的学科。初中数学是一个衔接的阶段，学生只有在中学时代打好基础，做好知识的巩固，学习更高层次的数学时才能更得心应手。华罗庚曾经说过：“数形结合百般好，隔离分家万事休。”随着我国教育改革的不断深入，找到合适的方法进行中学数学教学成为了教好中学数学的首要任务。在此基础上，本文对数形结合思想在初中教学的渗透路径进行展开分析。

关键词：中学教育;思想方法;数形结合;分类讨论;化归思想

前言

随着我国教育行业的不断发展以及新课标的推行，家长们对学生的成绩要求也越来越高。数学作为最基础的一科也最受到家长重视。初中的数学比起小学难度有较高的跨越，学生们的思维也处于过渡阶段，传统的教学方法不再适用。如果只针对应试技巧以及考试题型进行强化訓练，学生们即使能取得好成绩，也不会对数学进行真正的了解，更不会产生兴趣，就造成了“只求分不求知识”的局面。只有在思想上进行数形结合的渗透，让学生掌握知识点，提高学生的理科思维能力，才算是真正意义上的教学成功。

一、数形结合在初中数学中应用的教学现状分析

（一）初中课堂上忽略了数形结合思想的渗透或渗透不到位

由于师资力量不足、教师老龄化等诸多原因，绝大多数中学教师并没有进行思维教学的意识，只是遵循老教学方法将课本知识对学生灌输，强化应试解题技巧，进行题海训练，儿忽视了数形结合思想。数形结合思想与普通的教学概念不能同一而论，这考验教师的能力水平，无法短时间内进行改进。

（二）教师进行数形结合思维教学时方法固化

在教育学领域，固守一套教学方法不进行改进创新的事情屡见不鲜，死守课本知识，不进行发散思维。教师机械地将课本上的知识点挪到PPT上，看似结合多媒体沿用了新教学技术，实际上“换汤不换药”最终还是老教学方法。这使得一部分学生丧失对数学的学习兴趣，课堂效果也会大打折扣。

（三）在数学复习中忽略了数形结合思想

在课后对数学知识进行温习时，教师很容易陷入盲目刷题的盲区，一遍一遍让学生做题后修正错误，却忽视了将题型进行分类总结。这样的方式虽然使得学生有了一定的熟练程度，但却造成了学生“只会做题，不会思考”的现象，会使学生在日后的新课教学中不在认真对待，而是指望复习时的“题海战术”，忽略知识的消化，只追求成绩的提升。在短时间内可能会使得学生成绩有较大的提升，但从长远看来是不可取的。

二、数形结合在中学课堂中应用教学策略探讨

（一）充分利用教学资源

教学资源分为显性和隐性，显性资源有网络上现成的课件、教学视频等等，教师可以在课前进行观摩学习，以起到改进自身教学质量的效果。现在绝大多数学校都实现了多媒体覆盖。教师可以充分利用多媒体，例如设计一个flash动画在课堂上进行展示，通过简单的人机交互更为直观的向学生们展现以往需要耗费大量口舌进行的较为抽象的数学概念定理公式，帮助学生更直观的理解数形结合。另外还可以在课本知识教授完毕时给学生们播放一段知识点的思维发散视频，既能避免学生在课堂上注意力不集中，又能发散学生思维，提高课堂的趣味性以及互动性。隐形资源是在课堂上生成，在课前不能得知的，比如学生在课堂上提出的问题反馈，学生们对讲授知识的接纳程度都是宝贵的经验财富，如果教师能养成课后写教学随笔，时常反思，那么课堂质量也会有较大的改进。

（二）以形化数，以数变形

数形结合的思想主要包括“以形化数，以数变形”两个方面。其应用大致可以分为两个方面：1.借助图形的生动性和直观性来阐述数之间的关系，即借助形为手段，求数作为目的，例如应用函数的图像推断该函数的性质;2.借助于数的精密性和规范严密性来阐明形的某些属性，即借助数作为手段，求形作为目的，例如应用曲线的方程精确地阐明曲线的性质等等。

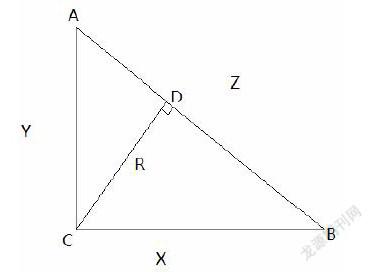
例如：已知XYZR均为正数，且X²+Y²=Z²，Z（X²-R²）½=X²，求证：XY=ZR。我们已知X²+Y²=Z²联想到勾股定理，做直角三角形。过直角做CD垂直于AB于B，由射影定理得CD²=AD·BD、BC²=BD·AB、AC²=AD·AB，得BD=（X-CD）½、X²=BD，X²=（X²-CD²） ½，CD=R。∴XY=ZR

数形结合在运用过程中也要注意如下两个原则，一是等价性原则，即代数与几何性质转换必须等价，同时既要进行几何直观分析，又要进行相应的代数抽象探求，仅分析代数容易出错。二是简单性原则，不要为了进行“数形结合”而进行数形结合。

（三）与时俱进，更新教育理念

在当今时代，随着对素质教育要求逐渐提高，老师作为学生的领路人，肩负着重要责任，这就要求教师要改掉以前满堂灌、填鸭子的教学方式，不断尝试新的教学方法，调动学生对数学的兴趣，培养学生逻辑思维，提高解题能力，全面提升学生数学素养，敢于创新、勇于创新，使课堂生动有趣。

结束语

数形结合思想在中学数学中有着举足轻重的地位，符合新课标教学要求，也是中学生学好中学数学的基石。想要改变当今数学课堂乏味、不注重思想的现状需要教师灵活将数学思想穿插到平日的课堂教学之中，无论是课前导入、习题演练亦或是课后总结，都渗透数形结合的思想，这样才能使得学生在学习过程中更有趣味性，进而真正掌握数形结合方法。

参考文献：

[1]刘爽，卢林霞.中学数学教学中渗透数学思想方法的实践与思考[J].中学课程辅导（教师通讯），2021（05）：53-54.

[2]陶玉娥.数形结合思想在初中数学教学中的渗透路径[J].科学咨询（教育科研），2021（05）：252-253.

[3]陈莲妹.论数形结合思想在初中数学勾股定理教学中的渗透与应用[J].科学大众（科学教育），2020（07）：19.

[4]谭东玲.高中数学教学中数形结合思想的应用现状及策略研究[J].数学大世界（中旬），2020（08）：14.