基于可释放动能的双馈风机虚拟惯性控制策略影响分析

高蒙楠，秦文萍，王丽彬，王科，张宇，朱志龙

（1.电力系统运行与控制山西省重点实验室(太原理工大学)，山西省太原市 030024；2.国网山西省电力公司经济技术研究院，山西省太原市 030002）

0 引言

风能资源在我国十分丰富，比如东部沿海以及西北地区，现如今电力系统中的风电渗透率逐渐增长，越来越多的风力发电必然会给电力系统的安全与稳定带来新的问题，因此风电接入对电力系统暂态稳定性的影响受到了广泛关注[1-2]。目前占主导地位的变速风电系统为达到获取最大风能的效果，通常工作在最大功率跟踪（maximum power point tracking，MPPT）模式。这也就使变速风电机组的转速与系统解耦，其旋转动能被“隐藏”起来，导致风力发电机组无法对系统提供惯性支撑功能。电网中如果出现大扰动，电力系统的频率以及暂态功角有较大概率发生失稳，进而影响风电机组的安全与稳定[3-4]。为了解决该问题，多个国家在其风机并网规范中规定了风力发电场需要具备和常规发电厂类似的惯性支撑功能。

目前，已有诸多文献分析了双馈风力发电机（doubly-fed induction generator，DFIG）虚拟惯性控制策略及其对频率特性的影响。文献[5]提出一种风-火系统自适应虚拟惯量策略，使得风电机群能够适当地参与到系统的频率调节中，有效地改善了电网的频率稳定性，但未考虑转速限制；文献[6]通过分析调频参数在电网频率调节中的作用机理，针对其影响模式的不同，提出了一种利用选择函数来控制其输出增益进而达到风机惯量控制的策略，并且限制了转速大小以避免风机转速越限造成的启停频率过高的情况，有效增加了系统等效的转动惯量，提高了频率稳定性，但未考虑在不同风速下其频率支撑性能；文献[7]首先分析了不同风况下的限功率模式，然后以变风速下的参数为变量，提出一种惯性系数跟随风速变化的惯性控制策略，提高了DFIG的调频能力。但其只对低于和高于额定风速进行了仿真，未考虑风机工作于MPPT不同风速区间的情况。上述文献通过虚拟惯性控制改善了系统的调频能力，但均未对附加虚拟惯性控制的DFIG并网功角稳定问题进行分析。

针对DFIG接入对系统暂态功角稳定性的影响，文献[8]从DFIG暂态特性出发，分析了其接入系统的等效模型，并基于此分别研究了等容量替代和直接并网下的同步机功角变化情况，然后针对不同风电渗透率等因素分析了其影响；文献[9]通过分析风电机组的励磁及暂态特性，针对风机并网后对系统暂态电压及功角特性表现出的不同影响形式做了比较；文献[10-11]提出了一种DFIG简化模型，利用扩展等面积定则和直流潮流计算方法分析DFIG接入两机系统后暂态功角稳定性的变化，同时考虑同步机出力、风电接入比例和风机接入电网的位置对系统暂态功角稳定性的影响[12]。以上文献较为详细地分析了风机并网的系统暂态功角稳定性问题，但都缺乏与调频特性相结合的暂态稳定性分析。

通过附加有功功率控制，DFIG中的变换器能够以虚拟惯量的形式对系统提供惯性支撑能力，其耦合了频率及机组参数波动情况。有功控制通过测量频率变化使得风电机组具备了与同步机类似的调频特性，提高了其调频能力。但由于附加控制可以改变惯性的大小，并网系统的暂态功角稳定性会伴随着惯性的变化出现不同程度的波动，系统故障时尤为明显[13]。然而在目前通过附加虚拟惯性控制来改善系统频率特性的文献中，同时研究其对暂态功角稳定特性影响的较少。

针对上述问题，本文首先根据DFIG数学模型推导出其等效功角的表现形式，并分析了DFIG的调频能力及功角特性间的关系。然后在经典惯性控制基础上提出考虑转子转速变化的基于可释放动能的双馈风电机组惯性控制策略。基于实时数字仿真系统（real time digital simulation system，RTDS）搭建了DFIG单机并网仿真系统，对工作在MPPT模式下不同风速区间的DFIG进行仿真验证。仿真结果表明本文所提虚拟惯性控制策略在改善频率特性的前提下兼顾提高了系统的暂态功角稳定性，提高了系统运行的安全性和稳定性。

1 双馈风电机组模型及其特性

1.1 双馈风电机组模型及功角特性

双馈风电机组的暂态特性与其组成密切相关。DFIG主要由一个感应发电机和两个背靠背变换器组成[14]。根据d-q旋转坐标轴下的DFIG模型，定子和转子侧电压方程如式（1）所示

式中：Usd、Usq表示定子电压的d、q轴分量；Urd、Urq表示转子电压的d、q轴分量；Isd、Isq表示定子电流的d、q轴分量；Ird、Irq表示转子电流的d、q轴分量；ψsd、ψsq表示定子磁链的d、q轴分量；ψrd、ψrq表示转子磁链的d、q轴分量；Rs、Rr为定子、转子电阻；ω为坐标系角速度；ωs为滑差角速度。

定子和转子侧磁链方程可以表示为

式中：Ls、Lr表示DFIG定子电感和转子电感；Lm表示定转子间互感。

结合式（1）和式（2），Usd和Usq可以改写为

式中：X'为等效电抗，计算如下

DFIG的转子侧变换器采用定子磁链定向控制策略，实现有功功率和无功功率的解耦控制；网侧变换器用于维持直流环节电压恒定。因此，通过机端电压、电流、磁链等变量，构造DFIG的等效内电势E'：

考虑到X'远大于Rs，忽略定子压降，则DFIG的等效内电势为：

由式（6）可得，DFIG具备了与同步电机的暂态内电势E'和端电压Us之间的类似形式的关系。与同步发电机的功角概念类似，将E'和Us之间的夹角δeq定义为DFIG的等效功角。DFIG定子电压矢量图如图1所示，说明了在d-q旋转坐标系中，E'和δeq之间的关系，其中d轴指向转子磁链ψr方向。

图1 双馈感应电机d-q旋转坐标系矢量图Fig.1 Vector diagram of DFIG in d-q rotating coordinate system

1.2 双馈风电机组调频特性及其与功角特性的关系

与同步电机不同的是，DFIG为了获取最大风能遵循最大功率跟踪控制，不具备系统出现扰动时的惯性响应能力。当系统出现有功扰动时，由于转子侧变换器的输出功率只能根据风机转速的变化来进行调整，无法响应系统中有功功率的变化。故若使DFIG具备与同步电机类似的响应电网频率变化的惯性支撑能力，需将电网频率的变化引入DFIG控制系统中。当频率发生变化时，首先功率控制快速响应，发出或者吸收系统中的有功功率，然后通过对转子转速进行控制来达到控制释放或者吸收发电机转子旋转动能的目的[15]。

文献[16]分析指出风电接入会影响系统的功率特性曲线，导致加速面积和减速面积改变，进而影响系统功角稳定性。但是并未考虑附加虚拟惯性控制的影响。随着风电渗透率逐渐升高以及并网控制技术不断发展，DFIG响应频率变化的虚拟惯性控制在风电友好并网环节中发挥了关键作用。附加虚拟惯性控制的DFIG可为电网提供一定量的虚拟惯性。当电网发生功率扰动后，DFIG附加的虚拟惯性控制策略会因检测到频率的波动而启动，通过改变输出功率的分布及大小，进而改变发电系统的功角特性。因此，附加虚拟惯性控制的DFIG调频特性与其暂态功角稳定问题密切相关，在研究频率控制的同时，也应注重于开发虚拟惯性控制策略在改善系统暂态功角稳定性方面的能力，使风电机组能够通过控制策略向系统提供更为灵活的功率支撑能力，对提高风电并网的暂态稳定性意义重大。

2 双馈风电机组的虚拟惯性控制策略

2.1 经典虚拟惯性控制

通过虚拟惯性控制使DFIG在系统频率突变时能够具备一定的可控惯性响应能力，参与系统调节。

双馈风机的经典惯性控制如图2所示，DFIG的控制系统包含了两个额外的控制回路：频率变化率df/dt回路和下垂Δf回路，Kdf和Kpf分别表示频率变化率回路和下垂回路的增益。DFIG转子侧变换器的有功输入由最大功率跟踪有功输出和两个惯性控制回路有功输出3部分组成，其中惯性控制回路通过测量系统频率并与额定频率做比较得出所在回路有功输出[17]。

图2 双馈风机经典惯性控制框图Fig.2 Block diagram of classical inertia control of DFIG

图2中:Popt为DFIG运行在最大功率跟踪模式下的有功输出；Pref为输入到转子侧变换器控制环节的有功参考值；ΔP为惯性控制环节的有功增益。故可得到以下关系：

式中：Δf为测量频率f与额定频率fN的差值。

由上述分析可得，当系统频率突变时，附加的惯性控制回路能够根据其测量频率和额定频率响应频率变化，通过控制转子侧变换器输入的有功信号，调节风电机组对系统注入或吸收的有功功率，故风电机组可以在系统发生扰动时惯性响应[18-21]。但风电机组在此控制策略下动态响应系统状态的过程中，无法考虑到其工作在不同区间的初始工况即转子转速情况。当系统因故障频率跌落时，风电机组会以增加有功输出的方式来响应频率变化，发电机转速因此降低。在MPPT模式下，不同的风速对应于不同的发电机转速。该控制方案只考虑频率变化情况，未将运行在不同风速下的发电机转速信息考虑在内，无法针对性地对运行在不同工况下的DFIG设置惯性控制增益。

综上，变速风电机组增加惯性控制回路后，能够通过附加有功增量调节其电磁功率，释放或吸收转子动能，使风电机组具有惯性响应能力。但由于该控制方案对不同风速下的风电机组转速不具针对性，使得该控制器缺乏灵活性，不能保证风电机组在扰动发生后能够保持稳定运行。

2.2 基于可释放动能的虚拟惯性控制

风电机组的最大功率跟踪特性曲线如图3所示。在不同的风速下，风电机组的运行曲线可以分为4个区域：启动区、最大功率跟踪区、恒转速区、恒功率区。DFIG在不同的转子转速下运行，其所具有的可释放动能也是不一样的。本文所提出的基于动能的虚拟惯性控制策略旨在最大限度地利用不同风速下DFIG中可释放的动能。

图3 最大功率跟踪特性曲线Fig.3 Maximum power point tracking characteristic curve

为实现本文所提控制目标，在DFIG控制器中构造了与图2相同形式的两个控制回路，这两个控制回路的增益是根据故障前的转子转速来调整的，以便在故障期间以更高的转子转速运行时DFIG能够释放更多的动能，如图4所示。

图4 DFIG基于可释放动能的虚拟惯性控制框图Fig.4 Releasablekinetic energy based block diagram of virtual inertial control

运行在较高转子转速区域的DFIG比运行在较低转子转速区域的DFIG包含更多可释放的动能。因此，为了从DFIG中释放更多的动能，所提出的方案根据其在故障之前的动能水平来区分DFIG的可释放动能。

1）下垂回路增益。

通过引入频率偏差下垂控制使风电机组表现出与常规机组类似的频率下垂特性。

DFIG可释放的动能ΔE可由下式定义：

式中：J为发电机的转动惯量；ω和ωmin分别为DFIG转子转速和最小转速限制。

如图4所示，为DFIG的下垂回路增益，且其平方与可释放动能ΔE成正比：

为得到上式的比例系数，可构建式（11）如下：

式中：ΔEmax是ΔE的最大值，可以通过将DFIG的最大转子转速ωmax插入式（9）来获得；R0是DFIG在最大转子转速下的比例常数。本文控制策略的目的是根据可释放的动能来确定DFIG的两个惯性控制回路增益，从而使DFIG释放较多的动能以提高频率最低点。然而，如果DFIG在附加虚拟惯性控制时由于增益较大而释放过多的动能，则转子转速可能降低到ωmin。在这种情况下，应禁用虚拟惯性控制以保护DFIG。这可能会导致输出功率显著降低，电网可能会出现频率下降情况。为了防止在惯性控制过程中DFIG的转子转速降低到ωmin，整理式（11）得DFIG控制环路增益如下：

根据MPPT模型的运行特性，本文将ωmin和ωmax分别设为0.6 pu和1.2 pu。一方面，对于转子转速较高情况下的DFIG，确定较小的R，以释放较多的动能；另一方面，对于转子转速较低情况下的DFIG，确定较大的R，以防止触发最小转速限制。

2）频率变化率回路增益。

本文定义K为频率变化率回路的增益且其平方与ΔE成正比，表示为：

整理式（13）得：

式中：K0是比例常数。

确定两个回路的增益前，需先选定R0与K0两个比例常数的值。由式（9）至式（14）可看出，R0与K0的取值与发电机的转动惯量（惯性时间常数）和转速有关，其取值不同则控制回路增益也不同，但增益过大有转子动能释放过度的危险。考虑到不同容量的发电机具备不同大小的转动惯量，当发电机惯性时间常数取值为1～20 s时，R0和K0取值在1.1～2.3之间，本文将R0和K0分别取为1.5和1.6。

根据上述分析可得，风电机组运行于MPPT模式，不同风速下机组具有不同转速，通过转速信号计算得出回路增益大小。高风速下的机组具备较高转速，其回路增益也较大，从而能够释放较多的转子动能；低风速下的机组转速较低，其回路增益较小，使其释放较少的动能，避免触发最小转速限制。

3 算例分析

为验证本文提出的控制策略，利用RTDS/RSCAD仿真软件建立了如图5所示的DFIG仿真系统，仿真参数如表1所示，并根据1.1节分析搭建等效功角模型。设定2.2 s时发生三相短路故障，故障时长为0.1 s。本文根据最大功率跟踪曲线设置最大功率跟踪区（风速取8 m/s，低风速）、恒转速区（风速取12 m/s，中风速）、恒功率区（风速取16 m/s，高风速）3种情况，并对经典惯性控制策略、基于可释放动能的惯性控制策略及无惯性控制下的调频能力和暂态功角稳定性进行仿真对比。

表1 相关参数Table 1 Related parameters

图5 单机无穷大系统拓扑图Fig.5 Topological graph of a single-machine infinite bussystem

3.1 低风速下仿真分析

图6显示了在最大功率跟踪区即风速为低风速8 m/s时，系统故障前后频率、发电机转速、风电机组有功输出及等效功角波动情况。结果如表2所示。

表2 低风速8 m/s时系统仿真结果Table2 Simulation resultsat low wind speed of 8 m/s

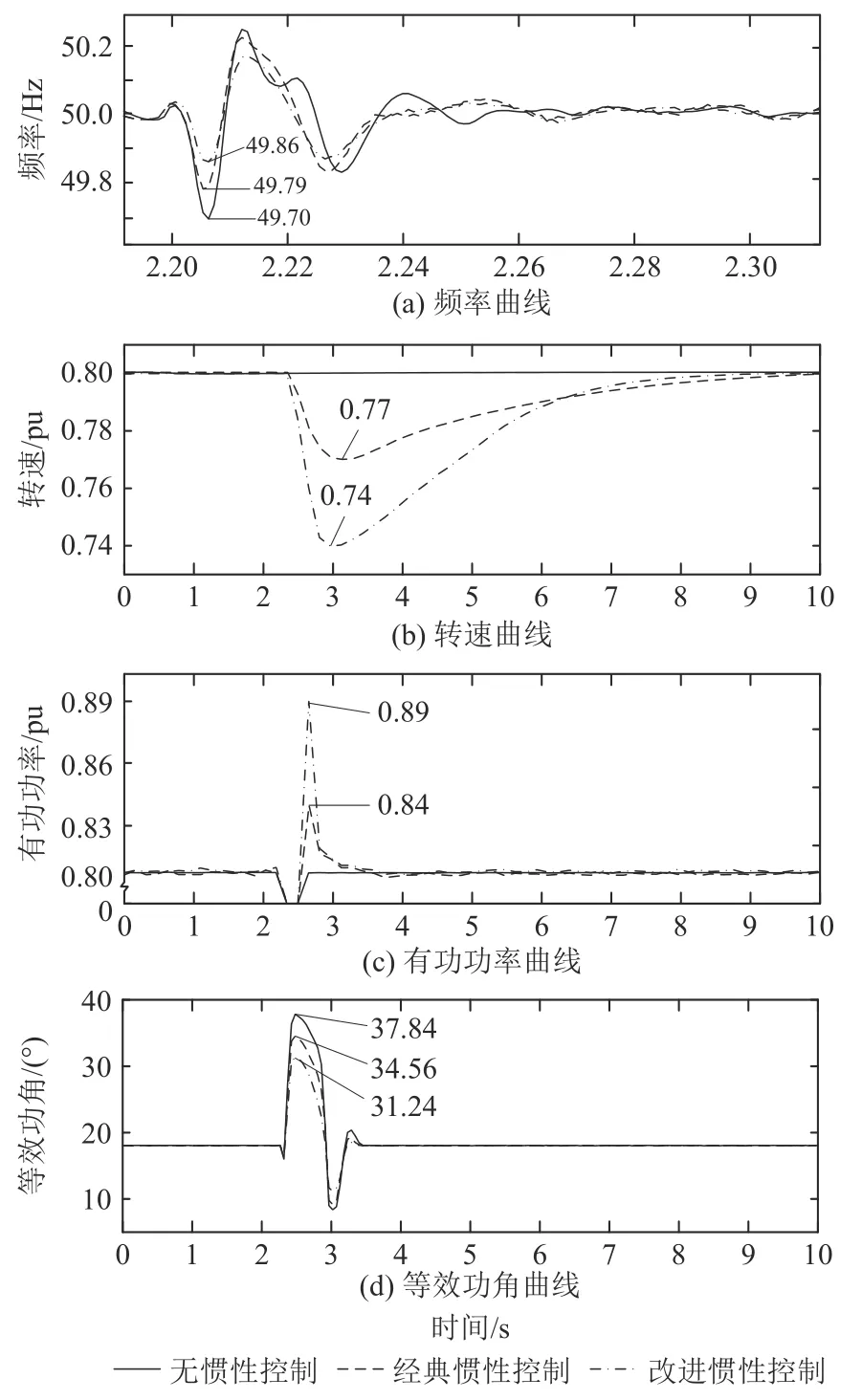
图6 低风速8 m/s时系统仿真波形Fig.6 Simulation waveform at low wind speed of 8 m/s

如图6（a）所示，在系统发生故障后，风电机组通过虚拟惯性控制策略可以参与调频使得系统频率的波动幅度和最大偏差减小。其中，无惯性控制下频率最低点为49.70 Hz，而经典惯性控制和改进惯性控制下频率最低点分别为49.79 Hz和49.86 Hz。对比两种控制策略，本文所提改进惯性控制策略能够进一步提高系统的频率最低点，使系统具备更佳的调频能力。

图6（b）和（c）分别为故障期间风电机组转子转速和有功出力的变化情况。由图分析得，当风电机组不附加虚拟惯性控制时，故障时其转子转速和有功出力不会响应系统频率的变化。而附加虚拟惯性控制后，故障时风电机组会通过降低转子转速释放部分动能来支撑频率恢复。

故障期间DFIG等效功角δeq的变化情况如图6（d）所示。系统故障时出现功率波动，δeq发生了振荡。风电机组通过惯性控制策略，增强了对系统的响应能力。在所提改进策略中，风电机组能够根据其转速大小，使其在不超过最小转速限制的前提下，尽可能多地释放转子中的动能用以提供有功支撑，有效改善了功角振荡情况。

3.2 中风速下仿真分析

图7显示了在恒转速区即风速为中风速12 m/s时，系统故障前后频率、发电机转速、风电机组有功输出及等效功角波动情况。结果如表3所示。

表3 中风速12 m/s时系统仿真结果Table3 Simulation resultsat medium wind speed of 12 m/s

如图7所示，当风速增加为12 m/s时，可以看出系统的频率稳定性有所提升，但是其恢复时间增加。这是因为随着风速的提高，风电机组整体的有功出力增大，相应的在故障时的短时有功出力同样增大，即风电机组短时释放的动能增多，但转速下降幅度同样增加。

图7 中风速12 m/s时系统仿真波形Fig.7 Simulation waveform at medium wind speed of 12 m/s

由图可得，对比低风速，中风速下的功角最大偏差较大。系统通过频率的波动来判断是否启动虚拟惯性控制，随着频率波动时间的延长，功角偏差同时也增加，暂态功角稳定性变差。

3.3 高风速下仿真分析

图8显示了在恒功率区即风速为高风速16 m/s时，系统故障前后频率、发电机转速、风电机组有功输出及等效功角波动情况。结果可见表4。

表4 高风速16 m/s时系统仿真结果Table 4 Simulation results at high wind speed of 16 m/s

图8 高风速16 m/s时系统仿真波形Fig.8 Simulation waveform at high wind speed of 16 m/s

由图表中的数据可得高风速下的系统频率稳定性要优于中风速但波动时间仍比低风速下长。在所提控制策略减小了功角最大偏差的基础上，高风速下功角的最大偏差要大于低风速下但小于中风速下的功角的最大偏差，说明高风速下暂态功角稳定性要略差于低风速但优于中风速下暂态功角稳定性。原因在于风电机组在最大功率跟踪模式下为捕获最大风能，一般认为其不留备用。在风速较高时，为了避免风机转速超出最大限值而破坏风机结构，必须通过桨距角控制将风机运行区间稳定在恒功率区。故其在最大输出功率处具备较好的稳定性，系统故障时有功出力增加；而在最大功率跟踪区和恒转速区也就是在低、中风速时，风机转速没有达到上限，若要使其获得有功备用，需要以主动收桨的手段来完成，这样又会牺牲掉风机的部分功率跟踪能力。

4 结论

本文提出了一种基于可释放动能的DFIG虚拟惯性控制策略，有益于在维持频率稳定的基础上兼顾暂态功角稳定。通过对比分析不同风速分区及不同控制策略下的频率及功角特性，得出以下结论：

1）不同风速下，运行在最大功率跟踪曲线下的风力机组的转子转速不同，其包含的可释放的动能也不同。

2）本文提出DFIG基于可释放动能的虚拟惯性控制策略，通过调整惯性控制回路增益与机组转速相关联，使运行在高转速区间的风电机组能够在系统暂态响应中释放出更多的动能，提供更多的有功出力，有效阻尼了系统频率及功角恶化，保证了系统稳定。

本文在单机无穷大系统中分析了DFIG附加虚拟惯性控制时不同风速区间下系统故障后的频率及功角变化情况。接下来将进一步研究风电渗透率、机组转动惯量等因素在更为复杂的双机或多机系统中对系统频率及功角稳定性的影响。