基于DBN和K-means聚类的配变重过载预警方法

童光华，董亮，任永平，于金平，冉新涛

（1.国网新疆电力有限公司电力科学研究院，新疆维吾尔自治区乌鲁木齐市 830011；2.国网新疆奎屯供电公司，新疆维吾尔自治区奎屯市 833200）

0 引言

配电网供电可靠性直接影响用电客户的满意度[1-2]，相关影响因素主要包括供电线路和配电变压器的故障率、作业停运修复时间、用户密度的分布、配电变压器重过载等[3-4]。随着经济快速发展，工业用电量、居民生活用电量都急速增长，配电变压器数量随之迅速增加；特别是7—8月、春节等时间段，由于用户用电需求的增加用电负荷剧增，引起大量配电变压器过负荷的运行状态，造成配电变压器非正常运行或故障[5-6]。某省电力公司运监中心数据显示，截至2017年10月，该省重载配电变压器设备已达255台，不仅给电网安全运行带来了较大的安全隐患，也造成了设备资产的严重浪费。

目前，配电系统运行产生的多源异构、规模巨大、增长快速、类型丰富的数据样本，表现出大数据的基本特征[5]。基于数据的机器学习是现代智能技术的重要组成部分，为配电变压器重过载问题的解决提供了新思路。采用基于数据的机器学习理论对配电网重过载变压器进行预测分析[6]，可以有效预测配电变压器未来是否会出现重过载现象。作为人工智能的分支，机器学习能够发掘已知数据的潜在规律对未来的数据发展做出预测，其中主要方法有支持向量机(support vector machine,SVM)算法[7-11]、人工神经网络(artificial neural network,ANN)算法[12-16]、深度学习算法[17-20]等。文献[7]基于SVM构建了模糊规则建模架构；文献[8-9]实现了基于最小二乘法的SVM；文献[10]实现了一种简化SVM；文献[11]给出了一种克服SVM失效的方法；文献[12]基于ANN实现了模型参数负荷预测；文献[13]基于递归ANN实现了短期负荷预测；文献[14]基于小波ANN实现了变压器油色谱时间序列预测；文献[15]采用小波模糊ANN实现负荷预测；文献[16]通过ANN方法对特定时间段，比如春节期间的重过载现象进行了预测研究，合理地反映春节期间配电变压器的负荷变化规律。目前用于配电变压器重过载预测的文献都是以短期预测为主，且均基于模型的训练样本量较充足的大前提下得出的，当样本数不够充分时，此类方法的有效性有待提升。SVM算法对大规模训练样本难以实施，用以解决多分类问题存在困难[17]；ANN存在局部极小化、算法收敛慢、结构选择不一、样本依赖性等问题。而深度学习算法提供了一种新的解决思路，可解决有限样本的学习问题。

本文采用深度信念网络(deep belief network，DBN)研究配电变压器重过载的小样本精确预测问题。

1 配电变压器中长期重过载预警模型分析

1.1 重过载的定义

配电变压器重过载预警的目的在于提前约3个月识别出可能发生重过载的配电变压器，及时对可能重过载的配电变压器进行维护或更换。由于已识别的配电变压器无论是重载还是过载，均需要进行更换，因此首要目的在于预测可能重过载的配电变压器，而不细分其过载还是重载。文中配电变压器负载率大于70%持续1 h，即判断为重过载现象，如图1所示。

图1 配电变压器发生重过载的定义Fig.1 Overload definition of distribution transformer

1.2 重过载中长期预警模型的构建

由于需提前3个月识别可能重过载的配电变压器，本文为中长期预警建立的模型，通常有两种实现思路：一是建立中长期负荷预测模型，预测配电变压器未来3个月后的负载率，若出现连续1h负载率预测值大于70%，则判断该配电变压器发生重过载。该模型构建训练样本容易、计算简便，但中长期负荷预测精度较低，提前一天预测误差约10%，提前3个月预测难以保证精度，且需具有较长时间段的历史数据样本（通常5年以上）。因此中长期预测模型难以有效判断3个月后的配电变压器重过载情况；二是建立二级分类模型，通过输入历史负载率峰值、负载增长率、配电变压器台账信息等特征，计算输出0或1（1等于会发生重过载，0等于不会发生重过载）。

假设N个样本组成的训练样本为{0,1}，每个样本独立分布，ti为样本标签，其决策函数：

式中：K(x,xi)为 核函数；wi={w0,w1,···wN}是模型的权重向量。将y(x)通 过logistics sigmoid σ(y)=1/(1+e−y)函数映射到[0,1]区间，即可得到二分类模型分类结果。

二分类模型可直接判断某配电变压器器是否重过载、比预测模型有更好的识别精度；但该模型实现的前提是有类似输入输出的样本作为训练。因此，选取输入特征、构建样本，是本文需要解决的另一个问题。

1.3 输入变量特征选取

建立二分类模型，需要输入-输出对应的样本，即同时需要重过载样本和未发生重过载的样本，其输出0或1。本文考虑4种类型的输入特征：历史负载率、设备台账信息、环境因素、社会发展统计因素。

2 输入变量特征筛选

由于多种维度特征变量均会影响配电变压器重过载的发生，本文考虑如表1所示的影响因素，具体结构如图2所示。

图2 配电变压器重过载的影响因素(输入特征变量)Fig.2 Influencing factors of heavy overload in distribution transformer

表1 配电变压器重载的影响因素Table1 List of influencing factorsof heavy overload in distribution transformer

由于输入特征变量数目众多，为了选取有效的特征变量、减小输入变量的冗余度，首先对上述特征变量进行相关性分析，以精选出反映配电变压器重过载发生特征的输入变量。

2.1 负载率特征变量

负载率特征变量属于数值型特征，为了研究其与发生重过载的相关性，计算皮尔逊(Pearson)相关系数[21]和互信息(mutual information,MI)两个指标，Pearson相关系数反映的是特征变量之间的共线性相关程度，MI反映的是特征变量之间的概率性相关程度，公式如下：

式中：Cov表示协方差；Var表示标准差；（xi，yi）为样本点；X为相应的负载率特征变量；Y为是否发生配电变压器重过载，值为0或1（即重过载和未发生重过载）；n为训练样本的数量；符号“—”表示样本均值；H(X)为MI的最大值；H(X|Y)表示在已知Y的情况下，X的不确定度；p表示xi和yi相关性的概率分布。Pearson取值在[−1,1]，其绝对值越大，相关性越强；MI取值范围为[0,1]，取值越大相关性越强。

根据式(2)、式(3)计算得到负载率特征的相关性如表2和图3所示。

通过表2的计算结果，发现负载率同比增长率对重过载发生的相关性较小，其他变量对重过载具有一定的相关性；比较图3的箱型图，除了同比增长率特征外，其他的负载率特征变量分布归类相似，即重过载配电变压器的负载率特征变量中位数高于未重过载的配电变压器。因此，表2和图3的结果一致，经过分析选取Pearson>0.1且MI>0.05的负载率特征：最大负载率、平均负载率、负载率波动值(方差)、日平均负载率峰值和历史重过载次数。

图3 负载率特征变量相关性分析箱型图Fig.3 Box-plot of correlation analysis of load rate characteristic variables

表2 负载率特征变量相关性计算结果Table2 Computing resultsof correlation of load rate characteristic variables

2.2 环境特征变量

环境特征变量中，根据历史负载率最大时的最高/最低气温和历史平均气温为数值变量，可直接计算其相关性；季节、历史是否连续高温/低温和特定节日设定为标签变量，进行编码，计算其相关性，结果如表3和图4所示（环境数据采用北方某城市关于日期、天气、电价的记录）。

表3 环境特征变量相关性计算结果Table 3 Computing results of correlation of environmental characteristic variables

根据相关性分析结果，历史负载率最大时的最高气温、最低气温和季节标签与是否发生重过载有一定关联性，满足Pearson>0.1且MI>0.05。此外，由图4可知，配电变压其负载率最大通常发生在夏季和冬季；而重过载则在绝大多数情况下发生在夏季。

图4 季节特征变量分析Fig.4 Analysisof seasonal characteristic variables

2.3 设备台账特征变量

经过分析计算得到设备台账特征变量的相关性如表4和图5所示，可知设备所在市县的特征变量对是否发生重过载具有一定的相关性。其中，全部配电变压器样本在5个市县的数量差异不大；而历史发生重过载的配电变压器样本中，高邮配电变压器样本数量最多，约占重过载配电变压器样本的50%。

图5 区县特征变量分析Fig.5 Analysis of county characteristic variables

表4 负载率特征变量相关性计算结果Table4 Computing resultsof correlation of load rate characteristic variables

2.4 经济和社会发展的统计数据特征变量

该类统计数据特征均为数值型变量，X为经济和社会发展的统计数据特征变量，Y为是否发生配电变压器重过载，计算Pearson和MI结果如表5所示。

从表5可知，社会发展统计数据与重过载的相关性普遍较小。综合分析后选取Pearson>0.08且MI>0.01的特征变量为住宅投资增长率、全社会用电增长率和第一产业比重。

3 基于DBN的配电变压器重过载预警方法

3.1 深度信念网络原理

图6为三层受限玻尔兹曼机(restricted Boltzmann machine，RBM)结构，V1为连接观测数据的可见层，H1为隐含层，用于提取输入数据有效特征，W1为可见层与隐含层的连接权重[13,22]。

图6 中长期重过载预警的DBN结构模型原理Fig.6 The principle of DBN structural model for mediumand long-term heavy overload early warning

RBM是一种基于能量的模型，用vi表示可见层神经元i的状态，对应偏置值为ai，用hj表示隐含层神经元j的状态，对应的偏置值为bj，神经元i和j连接权重为wij，状态(v,h)确定的RBM系统所具有的能量可表示为：

由能量函数可得(v,h)的联合概率分布：

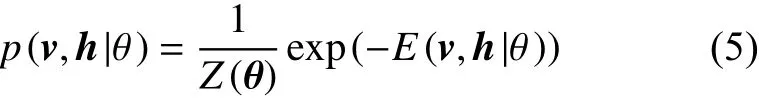
数量为N的训练样本，参数θ通过学习样本的最大对数似然函数得到：

由于RBM层内各神经元激活状态之间是相互独立的，因此，根据可见层神经元状态计算隐含层第j个神经元，激活概率：

由隐含层重建可见层第i个神经元，激活概率：

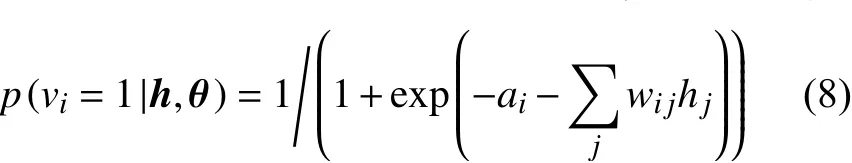
用随机梯度上升法求解对数似然函数最大值，各参数变化量计算准则[20]：

式中：〈·〉data为原始观测数据模型定义的分布；〈·〉recon为重构后模型定义的分布。

考虑学习率 ε的参数更新准则：

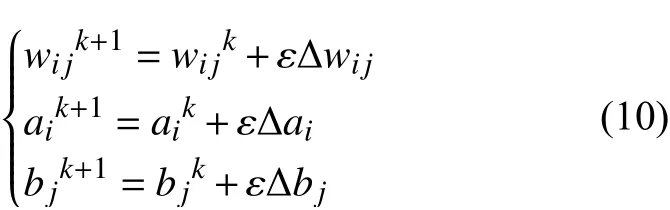
式中：h表示可见层输入，代表影响配电变压器重过载的特征变量输入；v表示隐含层输出，结果为0或1，分别表示配电变压器未发生重过载或将发生重过载；其余变量为模型的中间变量和训练参数。

3.2 基于K-means的配电变压器年负荷曲线聚类方法

选用K-means方法实现配电变压器的年负荷曲线聚类，其算法实现步骤：

步骤1）选择k个类初始中心；

步骤2）进行迭代过程，即任意样本，求其到k个中心的距离，将该样本归到距离最短的中心所在类；

步骤3）计算均值以更新该类的中心值，计算公式：

式中：c为中心值；i为属于该类的样本数量；Xc为该类中心样本均值；Xi为第i个样本；

步骤4）对于所有k个聚类中心，经过步骤2与步骤3迭代法更新后，中心值收敛，则迭代结束，否则继续迭代。

4 算例测试验证

4.1 预警模型识别结果

输入特征变量的筛选结果如表6所示。

表6 影响配电变压器重过载的精选特征变量列表Table 6 List of selective characteristic variablesimpacting heavy overload of distribution transformer

本文分别采用支持向量分类器(support vector classifier，SVC)、ANN、DBN分类器搭建重过载预警模型，进行5折交叉验证，得到各分类器模型的准确性如表7所示。分类准确率ACC和漏检率FAL的计算公式：

表7 重过载预警模型的交叉验证准确性Table 7 The cross-validation accuracy of heavy overload early warning model%

式中：Ncorrect为分类正确的样本个数；Ncv为验证折中的样本个数；NP为重过载的样本个数；NFP为实际重过载而未检测出来的样本个数。

经过交叉验证算例仿真分析，基于深度学习的DBN模型可以更好地学习输入特征与输出间的映射关系，因而具有更高的分类准确率和更低的漏检率，分别为78.11%和27.42%，有效地为中长期重过载起指导作用。

4.2 基于负荷曲线聚类的重过载结果深度分析

根据表8的重过载配电变压器清单，基于统计技术分析其分布特性如图7所示。对于扬州地区，从统计分析结果可以看出，配电变压器清单中约54%的重过载配电变压器位于高邮市；重过载配电变压器的额定容量，主要为100～200 kVA和300～400 kVA，其中200～300 kVA的配电变压器数量很少，小于1%；分析配电变压器下的低压用户数，绝大多数的重过载配电变压器下用户数小于100户，占比88%；从配电变压器所属配电网类型来看，大部分重过载配电变压器属于农网，占比78%。统计结果很好地反映重过载配电变压器特性，其中低压侧用户数小于100户、农网类型的配电变压器发生重过载的可能性更多，需要提前预警防范。

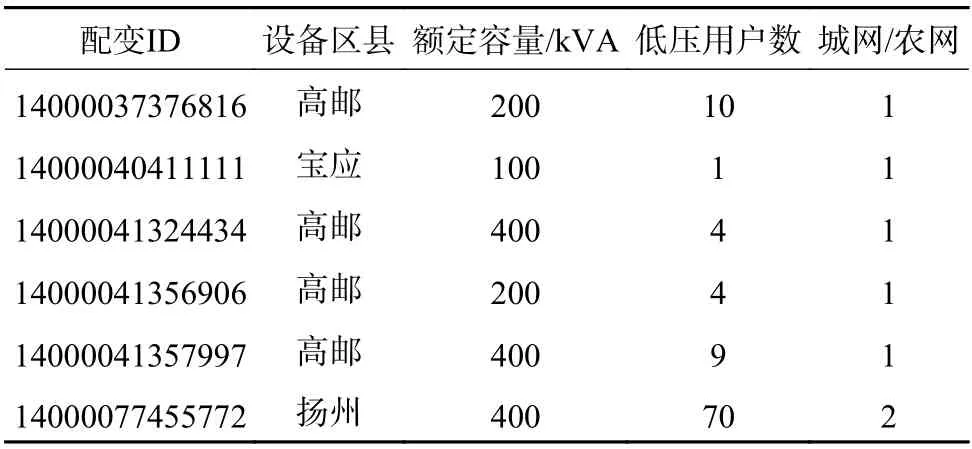
表8 预警识别重过载配电变压器清单Table 8 Detailed list of early warning identification for heavy overloaded distribution transformer

图7 重过载配电变压器分布特性统计分析Fig.7 Statistical analysison distribution character of heavy overloaded distribution transformers

为了深度分析其分布性规律，对不同类别重过载配电变压器曲线进行聚类分析。预警模型的识别时间跨度3个月，属于中长期分析，故选取年负荷曲线进行聚类分析，进而探究聚类结果对重过载的影响。考虑到负荷曲线类型受用户类型影响，不同区县的用户类型差异较大，对配电变压器负荷特性分别进行K-means聚类分析，以扬州市和宝应县为例结果如下：

1）扬州市区配电变压器聚类分析后具有两类年负荷曲线，如图8所示。

图8 扬州市配电变压器聚类分析Fig.8 Cluster analysisof distribution transformersin thedowntown of Yangzhou city

第一类年负荷曲线具有典型的夏季迎峰特性，其他时间段负荷趋于平稳、负荷率较低，该类负荷极容易在夏季发生重过载，且由于其他季节负载率较低，因此需要格外注意防范；第二类年负荷曲线较为平稳，受气温因素影响，在夏季和冬季的负荷率略高于春秋季，春节和国庆假期负荷率低，由于该类负荷平稳，因此对于其中的高负载率配电变压器需要加以关注。

2）仪征市聚类分析后得到如下3类年负荷曲线，如图9所示。第一类负荷曲线为夏季迎峰型曲线，在夏季具有最高的负载率，且负荷曲线差异较大，夏季负载率峰值远高于其他季节负载率，需要对其夏季迎峰时提前进行重过载预警；第二类年负荷曲线的波动性和随意性较大，通常情况下负载率较大，重过载可能性较小；第三类负荷曲线受到气温影响较大，在夏季和冬季的负载率均较高，但在春节假期负载率较低，由于负载率差异比第一类较小，故仅需对其中负载率较大的配电变压器进行重过载预警分析。

图9 仪征市配电变压器聚类分析Fig.9 Cluster analysis in Yizheng City

3）宝应县负荷曲线聚类特性结果如图10所示。

图10 宝应县配电变压器聚类分析Fig.10 Cluster analysis of distribution transformers in Baoying county

结果分为两类：第一类负荷曲线年波动平稳，受气温影响较小，国庆和春节假期负载率较低，仅需对负载率较高的配电变压器进行重过载预警；第二类曲线为夏季迎峰型曲线，在夏季负载率较高。

4.3 台区容量预警分析

经过上述重过载预警模型计算结果，结合不同市县的负荷曲线聚类情况，可以实现配电变压器容量的预警分析。限于篇幅，本文仅列扬州市配电变压器容量预警分析结果如图11所示，仪征市、宝应县、高邮市、江都区的结果不再赘述。

图11 扬州市配电变压器容量预警分析结果Fig.11 Resultsof early warning of distribution transformer capacities in the downtown of Yangzhou city

经过统计计算分析，扬州市负荷类型1夏季迎峰负荷更易发生重过载，占比60%；对于容量200 kVA以上、用户数100户以下的城网配电变压器，需要进行容量预警。

5 结论

本文实现了一种新的容量优化配电变压器重过载预警方法，基于深度学习算法建立预警模型，实现了配电变压器安全隐患预判。该模型可提供未来将发生重过载的配电变压器清单，便于运营人员及时维护，提升电网迎峰度夏、春节等负荷高峰期对配电变压器过负荷的预警和应急处置能力。算例分析表明，该模型能有效学习特征变量规律，实现对3个月后发生重过载配电变压器的准确预警。