基于改进云模型和Eclat算法的输电线路极端灾害风险评估

杜平，张小军，许永新，王永强，王立福，董新胜

（1. 国网新疆电力有限公司，新疆维吾尔自治区 乌鲁木齐市 830000；2. 国网新疆电力有限公司电力科学研究院，新疆维吾尔自治区 乌鲁木齐市 830011；3. 河北省输变电设备安全防御重点实验室(华北电力大学)，河北省 保定市 071003）

0 引言

近年来，我国电网发展迅速，对电网实施状态检修已经成为保障电网安全性和经济性的重要方式。架空输电线路作为电力系统的大动脉，其分布范围较广且地处自然环境复杂，是电网中的薄弱环节[1-3]。文献[4-5]指出自然灾害是导致我国电网发生缺陷以及故障的主要因素，架空线路处于恶劣的自然环境中，经常会遭遇雷击、风害、山火、冰害等极端灾害。所以，对处于极端条件中的输电线路进行全面、科学地风险评估，制定有针对性的检修策略，有助于保障电网的安全稳定运行。

目前，国内外众多学者针对输电线路极端灾害风险评估问题进行了深入的研究。文献[6]采用统计分析方法，得到了输电线路年故障率分布，对输电线路冰害故障进行了综合分析；文献[7]提出了一种基于层次分析法的输电线路山火预警模型，提高了山火防治效率；为了能够进行全方位的评价，文献[8-10]分别采用层次分析法、多元数据融合理论、灰色聚类的差异化运维策略等方法，考虑电网运行方式、输电线路设计信息、气象情况等在内的多维度因素对输电线路进行全方位的综合评价，并通过智能算法对输电线路进行故障诊断与状态分析，在工程实践中也取得了一定的效果；文献[11]通过动态回归神经网络和马尔科夫链模型构建基于卫星及气象信息的输电线路灾害监测与风险评估平台；文献[12]通过构建支持向量机的输电线路覆冰状态评估模型，对覆冰故障进行干预和排查。

虽然已取得了上述成果，这些方法仍具有一定的局限性：一是评估阈值的确定受人为主观因素影响较大；二是评价指标之间具有较强的关联性，基于多重技术因素的关联规则挖掘仍待研究。

本文中提出基于改进云模型和Eclat算法的输电线路极端灾害风险评估方法，该方法结合聚类模型、云模型和关联规则理论，实现了数据的量化整合与规则挖掘，可提高灾害风险评估的准确性。

1 极端灾害特征因子云处理

风灾、覆冰等极端灾害会对线路造成严重影响，根据“重要输电通道风险评估导则”，输电线路易遭受的灾害主要包括火灾、舞动、冰害等共11个风险技术要素。本文中选取11个技术要素中的冰害、风害、舞动3种对电网危害较大且具有关联特征的极端灾害作为研究对象，对多重风险技术要素的评估方法进行类比。引发以上极端灾害因素众多，采用单一指标监测数据无法对灾害等级进行精确评估与预测。本文选取气温、湿度、风速、导线温度、光照强度、气压、降雨量和降雪量等8个因素作为极端灾害特征因子。

由于在线监测数据和气象数据量较大，且各指标间的影响关系复杂，在进行风险关联分析之前需要对各特征因子的监测数据进行风险等级量化。由于云模型在处理数据的过程中兼顾了数据的模糊性与随机性，可以较准确地表达定量指标到定性指标之间的转换，因此，本文以云模型对各指标进行等级量化。具体地，将风险等级分为I、II、III、IV级，级数越高代表该指标引起某灾害的风险越大。当风险等级处于I级时，采用右半云模型；当风险等级为IV级时，采用左半云模型。标准云模型示意图如图1所示。

图1 标准云模型Fig. 1 Diagram of standard cloud model

云模型可用期望Ex、熵En以及超熵He来描述。其中：

式中：cmax和cmin分别代表某等级下灾害特征因子及各风险技术要素的最大值和最小值，该阈值的选取由专家根据相关导则确定；He根据各指标的不确定性来确定，经多次仿真验证，本文He取0.02。

云由云滴组成，每一个云滴是某一评价指标的定量实现[13]。得到云模型的数字特征后，生成一定数量的云滴，计算每个云滴属于某一评估等级的关联度y[14]：

式中：Ex为该云滴在某风险等级下的均值；En'是以En为均值，He为标准差所产生的正态随机数；x为以Ex为期望，En为标准差的正态随机数，即云滴。

2 改进的云模型

2.1 基于FCM聚类的客观云

云模型计算的关键是对灾害等级阈值的划分，而传统云模型是依据专家经验或导则阈值进行选取，专家经验或导则虽具有一定的普适性，但对于特定地区的特征因子及灾害风险技术要素阈值需要根据当地情况进行客观修正，若阈值不准，会对Ex和En造成影响，使标准云精度下降，影响等级量化。因此，本文对云模型进行改进，基于待评估地区的历史数据进行阈值的客观划分。

单个特征因子的历史数据为一维数据，本文采用FCM算法对一维数据进行聚类，在风险等级数确定为4个的情况下，应用FCM聚类算法，获取4个聚类中心，目标函数是4个聚类中心到历史数据中的所有点的距离之和最小，以4个聚类中心作为云模型中的4个风险等级的期望Ex，从而得到客观云模型。计算客观云的步骤如下：

步骤1）对单一特征因子历史数据进行去重处理，得到包含有特征因子历史极大值和极小值的一维数据序列Xobj={xo1、xo2、···、xon}；

步骤2）随机选择4个样本为聚类中心，分别为ci(0)，i=[1,2,3,4]；随机初始化每一个数据xoj对于ci(0)的隶属度uij(0)，形成隶属度矩阵，满足：

步骤3）当迭代次数iter小于最大迭代次数itermax时，根据下式对聚类中心ci和隶属度uij进行更新：

式中：m为模糊度的权重系数，一般取[1.25，2.5]，本文取m=2。

步骤4）判断是否满足终止条件，即：

或迭代次数为最大迭代次数；ε为误差精度；

步骤5）若不满足步骤4终止条件，则继续进行迭代；最终输出4个聚类中心，并依据指标风险从小到大进行排序，得到C=[c1、c2、c3、c4]；

步骤6）分别计算每个数据与4个聚类中心的距离，将数据分类至与其距离最小的类别中，取同一类别所有指标的最大值和最小值作为云模型对应等级的阈值。按照式（1）形成客观云模型的数字特征Exobj和Enobj。

2.2 动态风险修正

相同的灾害对不同的线路造成的影响后果是不同的。输电线路在遭受极端灾害天气后故障风险程度与外部环境风险有关外，还与线路自身的防灾减灾能力有关[15]，输电线路的防灾能力是指输电线路抵抗灾害所造成的损失和破坏的能力，与自身因素有关。

在进行风险评估时，应充分考虑输电线路整体设备的健康程度，本文根据Q/GDW1173—2014架空输电线路状态评价导则中的线路单元状态量评价标准进行扣分[16]，结合权重得到线路的评分值C1，将分数C1除以满分CS转换为最终的输电线路防灾能力指数C。

考虑风险造成的后果严重程度，本文采用停运时间修正指数τ来描述该地区对风险的综合处理能力，即灾害风险造成的经济性后果，指数τ是在灾害发生后对线路的抢修能力、交通能力等综合能力的反映，计算公式为：

式中：Tl为某种灾害造成的总停运时间；NL表示停运的总次数；TL为所有灾害发生造成的总停运时间；Nl为某种灾害发生造成停运次数。

输电线路在有效投运年限内，面对相同的灾害，其风险会随着服役年限的增加而增加。而相同服役年限的杆塔，灾害累积次数越多，风险会越大[17]，因此需考虑风险累积效应，计算风险累积指数h0：

式中：t为评估时，线路服役时间，单位为天；Te为线路设计运行时间，单位为天；α为有效灾害指数，通过采用参数估计获得；nIII为某灾害超过云模型III级风险最小阈值的次数，认为该灾害为极其恶劣，会造成风险积累。

对输电线路进行风险动态修正，得到风险动态修正指数β：

2.3 主客观组合云模型

得到客观云模型的数字特征后，为了使阈值划分更加合理，需要结合主客观数字特征。假设组合前主、客观云模型数字特征分别是(Exsub,Ensub)和(Exobj,Enobj)，用主、客观数字特征的平均值作为组合标准云模型的数字特征Exs和Ens。

随后对所有指标正向归一化处理：

式中：x为某指标的实际值；xmax为该指标组合云模型中最大等级阈值；xmin为该指标组合云模型中最小等级阈值；x′为指标归一化化后的值；（a）用于计算值越大，风险越大的指标；（b）用于计算值越大，风险越小的指标。

得到数字特征后，计算输电线路待量化分级指标数据x0在不同等级风险下的隶属度：

式中：x′0为归一化后的指标数据；β为该线路的风险修正指数；uη为指标在第η个风险等级下的隶属度；Exsη为第η个风险等级的均值；表示以Ens为期望、He为标准差的正态随机数。

根据隶属度最大原则，得到每个特征因子和技术要素的量化等级风险。

3 基于Eclat算法的风险关联规则挖掘

3.1 Eclat算法描述

由于历史数据积累的规模越来越大，各风险特征因子和技术要素之间包含复杂的内在联系。若能够对灾害特征因子量化后的数据之间的相关性进行充分挖掘，得到灾害特征因子与风险技术要素间的映射关系，根据在线监测数据和预报数据对未来可能发生的风险进行评估预测，可提高效率、节省人工。因此寻找一种既能处理大数据又能满足数据挖掘的算法至关重要。

Elcat算法是一种数据挖掘算法，它采用垂直数据结构形式，在读取一次数据库中的项目(Item)、事务标识符（Tid）数据的基础上遍历整个数据库[18]，对数据进行挖掘。文献[19]的研究表明该算法较经典数据挖掘算法Apriori效率高。

在该算法中，采用垂直数据表示的数据库定义为Tidset。对于数据集中的事务，对任意的项目X，把包含项目X的所有事务的ID放入一个新的集合，即项目X的Tidset。对数据库中的所有事物进行重新排列，每一记录由一个项目及所有事物记录的列表构成。以A、B、C为例的水平数据集合垂直数据集见表1和表2。

表1 水平数据集Table 1 Horizontal dataset

表2 垂直数据集Table 2 Vertical dataset

Eclat算法中所有单个项目的集合称之为1项集，取1项集中任意两个元素的交集作为2项集的元素，以此类推，产生κ项集。在各项集中每个元素的事务数称之为该项目的支持度sup。

Eclat算法的实现过程：

1）通过扫描数据集，把水平格式的数据库转化成为垂直格式的数据库；

2）计算第1项集中各项目的支持度，根据需要设置最小支持度minsup，当项集中的某项目小于minsup，会在项集中删除，其他项目重新构成第1项集L1；

3）将各个项目分别与后面的项目取交集，得到新的项集，计算各个项目的支持度，小于minsup的项目会在项目中删除；

4）以此类推，计算第κ个项集，直至不能再找到新的项集为止；

5）输出每一阶项集列表F[I]。

3.2 极端灾害风险关联规则挖掘

输电线路的风险评估过程中，记X→Y的过程为关联规则蕴含式，当X、Y同时出现在集合T中时，X与Y同时出现的次数记为该规则绝对关联系数cor（X→Y），定义规则X→Y的相对关联系数[20]：

定义规则X→Y的置信度：

式中：|D|为数据集的数量；cor（X）表示包含事务X的数据集总数。

风险关联规则挖掘过程中，设定rcor和conf的阈值，删除小于阈值的数据集，可得到关联度较大的规则，从而提高计算效率。

3.3 极端灾害风险评估方法

输电线路极端气象灾害风险评估目的在于能够更准确地认识风险，合理选择风险对策，形成最佳的风险应对策略。本文提出的基于改进云模型和Eclat算法的输电线路极端灾害风险评估方法整体流程如图2所示，根据风险评估结果安排相应的检修策略如表3所示。

表3 检修策略Table 3 Maintenance strategy

图2 输电线路极端灾害风险评估方法流程Fig. 2 Flowchart of extreme disaster risk assessment of transmission line

4 算例分析

4.1 模型建立与计算

为了具体说明文中所提出的基于改进云模型和Eclat算法的输电线路极端灾害风险评估方法，本文选取了新疆某地750 kV某线路中的10个易发生极端灾害风险的杆塔单元为研究对象，设定标号为1−10号，对其极端灾害风险进行评估，验证模型的合理性。

对于单一杆塔单元，调取在线监测数据并获取气象部门信息，得到待评价线路指标在某时间段的历史信息。本文选取了750 kV线路楚喀I线1号杆塔所在区域2019—2020年的实测数据，根据本文所述方法建立了主观云模型和客观云模型，为方便说明本文所述改进的云模型，以“风速”指标为例，采用FCM模型聚类后的结果如图3所示，“*”代表聚类中心，其值在图3中标出。

图3 聚类结果Fig. 3 Results of clustering

对于其他特征因子和技术要素，采用相同方法得到客观云模型；参考该地区历史资料、相关标准，邀请专家确定标准云模型的等级阈值，将指标归一化后建立标准组合云模型，得到各等级组合云模型的数字特征见表4所示。

表4 标准云模型数字特征Table 4 Digital characteristics of standard cloud model

依据该杆塔的设计资料，计算得到线路防灾能力指数，归一化后C等于0.89；历史数据，冰害共造成停运时间183.78h、风害共造成停运时间163.45h、输电线路舞动造成停运时间100.68h；该杆塔设计运行时间18250d，参数α等于1.005。根据评估时间不同，分别计算风险动态修正指数β；计算待评估数据各个指标修正后的风险，并在组合标准云模型中计算隶属度，选取“风害”评估后的模型如图4所示，“*”为当天待评估的数据点。

图4 “风害”等级量化云模型Fig. 4 Quantitative cloud model of 'Wind Damage'

4.2 模型评价结果

MATLAB中导入历史数据集，根据上述极端灾害风险评估方法编制云模型程序，计算每个指标在云模型中的隶属度，得到历史灾害量化等级，共619852条数据如表5所示。

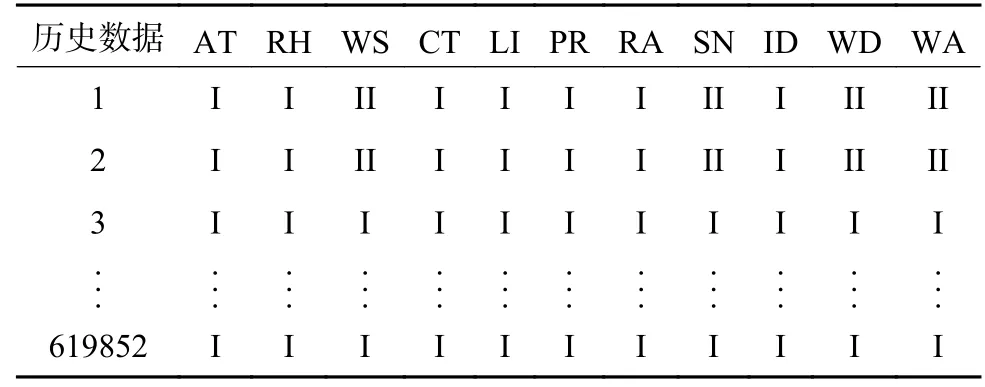
表5 历史灾害量化等级数据集Table 5 Quantified grade data set of historical disasters

为验证改进云模型的正确率，以人工巡检评估结果作为风险等级标准，选取与人工巡检评估相同时间段内传统云模型和改进云模型的评价结果进行对比，结果如图5所示。

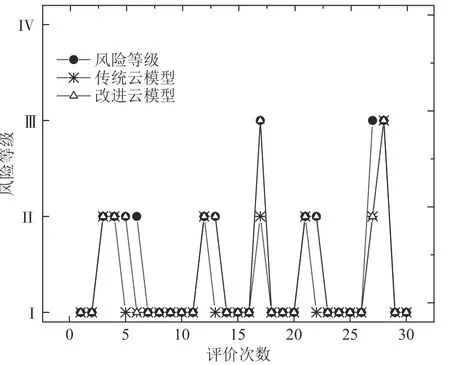
图5 改进云模型与传统云模型对比Fig. 5 Comparison between improved cloud model and traditional cloud model

结果表明，该杆塔30次历史评估过程中，传统云模型的准确率为80%，改进后的云模型准确率为93%，改进后的模型更接近实际输电线路风险。

将上述经改进云模型量化后的数据在Windows环境中，应用Elcat算法进行关联规则挖掘，多次试验并不断调整算法参数，设定置信度阈值0.5，相对关联系数阈值0.25，最终，选取部分含有风险技术要素的数据样本如表6所示。

表6的规则1表示当气温在II级风险、风速在II级风险时，线路会有II级冰害风险的概率为92.2%；规则2表示当相对湿度在III级风险、气温在II级风险、且有降雪时，发生II级冰害风险的概率为89.8%；规则3表示当风速风险在II级，且降雪风险等级为II级时，线路发生舞动的风险等级为II级，概率为88.6%；规则4表示当线路所在地区气压风险等级为II级、风速等级为II级时，线路会有95.3%的概率发生风害，风害等级为II级。

表6 部分关联规则Table 6 Partial association rules

得到关联规则后，运维人员可以根据该规则，在获取气象监测数据和预报数据的基础上，对线路灾害风险等级进行评估预测未来可能发生的灾害，做好灾害预防准备。

将本文模型应用于该线路的10级杆塔中，选取2020年某天的最终得到的该线路10级杆塔的灾害风险等级如图6所示。

图6 杆塔风险评估结果Fig. 6 Risk assessment results of tower

从图6中可以看出，该线路第2、3、4、8号在同一天出现冰、风、舞动等灾害风险，其中第8号杆塔的风害风险等级达到III级，查阅资料可知，当天为大风天气，并伴有降雨，平均风速达到12.5 m/s，极大风速为30.3 m/s（11级），大风导致导线与铁塔间安全距离不足，造成风偏故障，导致线路跳闸。

从结果看，本文提出的基于改进云模型和Eclat算法的输电线路极端灾害风险评估方法能够较传统云模型提高了单一杆塔量化等级的评估准确度，通过Eclat关联规则挖掘，能够得到多灾害特征因子和风险技术要素间的关联关系，从而依据该规则并根据现有数据对风险进行准确评估和预测，可减少人工工作量，该方法适用于输电线路的风险评估。

5 结论

1）本文基于FCM聚类算法根据灾害特征因子指标历史数据寻找聚类中心，结合专家主观评价得到风险评估等级阈值，考虑输电线路的抗灾害能力、灾害造成的平均停运时间以及风险的累积效应，对风险进行动态修正，对云模型进行改进，改进后的模型评估准确率较传统模型得到提升；

2）对云模型量化后的灾害风险等级应用Elcat算法充分挖掘关联规则，得到了线路灾害特征因子风险等级与风险技术要素间的内在联系；

3）基于新疆某地750 kV线路的实例分析，结果表明，本文提出的风险评估策略可基于历史数据进行评估，风险评估结果准确，较合理。