基于无源控制理论的准Z源超导磁储能系统

王进武，雷勇，刘晖，何平

（四川大学电气工程学院，四川省成都市 610065）

0 引言

超导磁储能(superconductivity magnetic energy storage，SMES)系统是通过直流的形式来进行能量的存储，SMES变流器是实现电力系统和超导磁体之间功率双向流动的关键部分。目前SMES是采用基于绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)等全控型器件组成的PWM变流器来进行能量转换，SMES变流器可分为电流源型变流器(current source converter，CSC)和电压源型变流器(voltage sourceconverter，VSC)这2种结构[1]。对于CSC，超导线圈(superconducting coil，SC)与CSC的直流侧直接连接，将超导线圈看作一个电流源，当其电感足够大时，超导线圈可以视为恒流源。由于其超导线圈直接与直流侧相连，电路结构简单、易于控制，但线圈自身的参数和动态性能会对系统输出功率的影响较大[2]。VSC通过将斩波器与变流器直流测电容并联来调节超导线圈两端的电压。相较于CSC，VSC可以实现超导磁体与电力系统的解耦，更有利于超导磁体的保护，无功补偿能力不受超导磁体电流的制约，无功补偿能力更强[3]。

传统的VSC输出电压范围有限，桥臂上下开关容易受干扰，从而造成直通而损坏。彭方正教授提出了Z源逆变器(z-source inverter，ZSI)的拓扑结构[4]，如附图A1所示。加入Z源网络后，逆变器多了一种直通状态，可以避免直通对变流器造成的损害，并且由于直通状态的加入，可以防止死区时间对输出波形的影响[5-7]。但传统Z源逆变器存在着Z源网络电容电压大于输入电压，造成电容体积和成本高；启动时容易产生冲击回路，逆变器易损坏等缺陷[8]。为了解决传统Z源逆变器的不足，国内外学者进行了一系列研究，提出了准Z源逆变器(quasi Z-source inverter，QZSI)[9]，如附图A2所示。QZSI采用非对称结构，通过调整电感的位置，使电感L2与直流电源串联，除了具有传统ZSI的特点外，还可以使Z源逆变器的输入电流连续，简化系统滤波电路，降低电容C2的电压应力和成本，同时减小元件体积。目前少有研究双向功率传输的准Z源变流器及其在储能变流器中的应用，结合SEMS系统的经济成本问题，将QZSC应用到SMES系统中以提升系统的稳定性具有研究价值。

变流器的控制策略直接影响整个系统运行的稳定性。控制策略可分为线性控制和非线性控制2类。比例积分(proportional-integral，PI)控制是一种常见的线性控制策略，PI控制器所需整定的参数较多且对参数的变化非常敏感，对于不同结构的系统均需要对相关参数进行重新整定，不适合对复杂的非线性系统进行控制，且在指令阶跃变化时响应时间和超调量较大[10]。常见的非线性控制策略主要有模糊控制[11-12]、反步法控制[13]和自抗扰控制[14]。模糊控制器是一种易控制、掌握的非线性控制器，具有较强的鲁棒性，但是模糊控制的设计尚缺乏系统性，模糊规则和隶属度函数的设计完全凭经验，控制精度较低。反步法控制在设计时计算量大且系统鲁棒性较差。自抗扰控制的控制参数多，目前还没有定量的参数设计方法。无源控制理论是在网络理论和其他物理分支中发展而来，是研究控制系统的有效工具之一。无源控制从系统的能量入手，寻求被控制量相关的能量函数，设计的无源控制规律可使能量函数按期望的能量函数分布，从而来达到控制目的[15]。同时使用无源控制理论设计的系统无奇异点问题，具有较强的鲁棒性[16-18]。将无源理论应用到SMES这种非线性、强耦合的系统中来提高系统整体的鲁棒性有较深的研究意义。

准Z源逆变器无法实现能量的双向传输，为此，本文对准Z源逆变器进行改进，使能量可以在交直流侧进行双向流动，提出QZSC-SMES的新型超导储能系统拓扑结构，并在双向准Z源变流器的直流侧和交流侧提出基于无源理论的控制策略。

1 系统结构及工作原理

1.1 拓扑结构

准Z源SMES系统的拓扑结构如图1所示。图中：L和R表示变流器交流侧电感值和电阻值；ua、ub、uc分别表示三相交流相电压；Sa1-Sa2、Sb1-Sb2、Sc1-Sc2分别为A、B、C三相桥臂上的全控型开关管的状态变量，1表示闭合，0表示断开；L1、L2和C1、C2分别为准Z源网络的电感值和电容值；C3为直流侧稳压电容值；S1为带反并联二极管的全控型开关；S2、S3为斩波器开关管、D1、D2为斩波器续流二极管；Lsc为超导储能线圈电感值；ia、ib、ic为三相交流电流；udc为电容C3的电压；isc为超导线圈的电流。

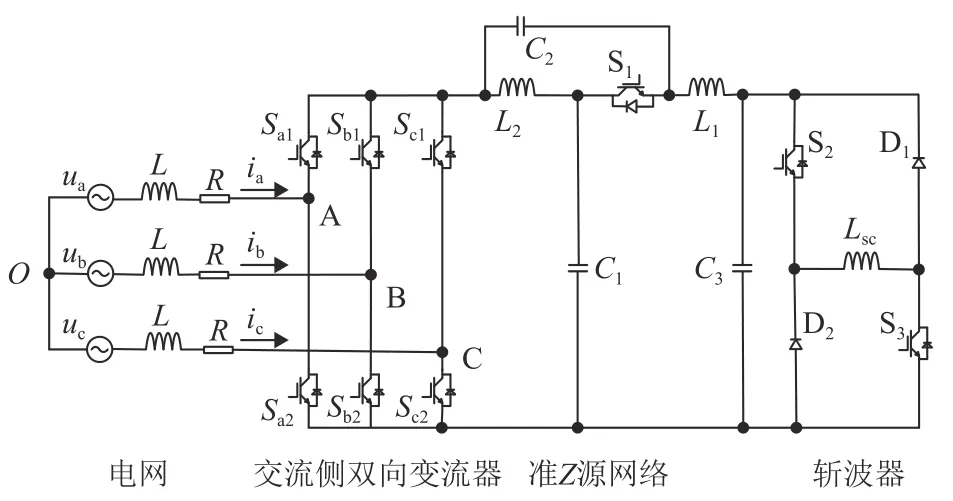
图1 准Z源SMES系统拓扑结构Fig.1 Topological structureof QZSC-SMESsystem

1.2 工作原理

图1中，QZSC-SMES系统由双向AC-DC变流器、准Z源网络以及直流侧斩波器和超导储能线圈组成。与传统准Z源网络不同的是，将传统准Z源网络中的二极管换成了带反并联二极管的全控型器件，来保证能量的双向流动。对图1的拓扑结构进行简化，分析准Z源网络在一个开关周期内的工作原理。将变流器三相桥电路等效为电流源和一个理想开关并联的结构，直流侧电容和斩波器等效为一个直流电压源，如附图A3所示。

附图A3(a)、3(b)中，开关S闭合表示准Z源变流器上下桥臂直通的状态，S断开表示变流器非直通状态。当开关S闭合时，若系统整流，S1关断；系统逆变时，S1并联的二极管承受反向电压关断。当开关S关断时，开关管S1则根据系统的工作模式进行通断。综上，当变流器直通时关闭开关管S1；当变流器非直通时，准Z源网络中S1驱动信号通过将空间矢量脉宽调制（space vector pulse width modulation，SVPWM）的 输出信号通过与非逻辑得到，从而实现对超导线圈充放电的控制。

2 QZSC-SMES控制策略

2.1 交流侧控制策略

2.1.1 变流器数学模型

如图1所示，变流器的每相桥臂有上下2个开关管，用Sk表示开关管的状态，其中k=a、b、c。则变流器开关状态函数为

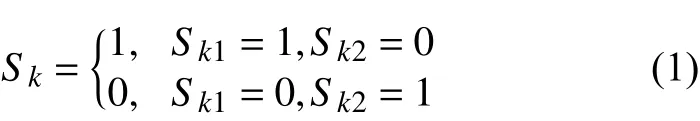
运用基尔霍夫定律，可得变流器交流侧在abc坐标系下的数学模型为

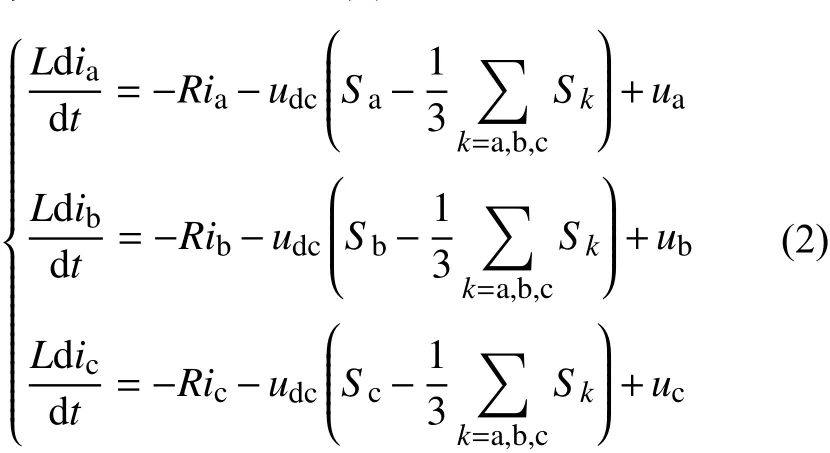
将abc三相坐标系下的数学模型通过坐标变换，得到变流器在dq坐标系下的数学模型为

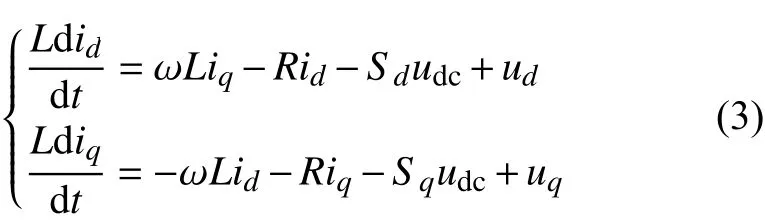
式中：id、iq为dq坐标系下变流器电流值；ud、uq为dq坐标系下的电网电压；Sd、Sq为dq坐标系下的开关函数。

将式(3)写成无源控制的E-L方程：

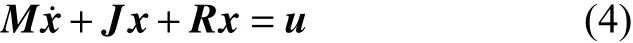
式中：M为正定的对角矩阵；J为反对称矩阵，J=−JT，反映了系统内部的互联结构；R为对称矩阵，反映了系统的耗散特性；u表示系统与外部能量交换。

其中：

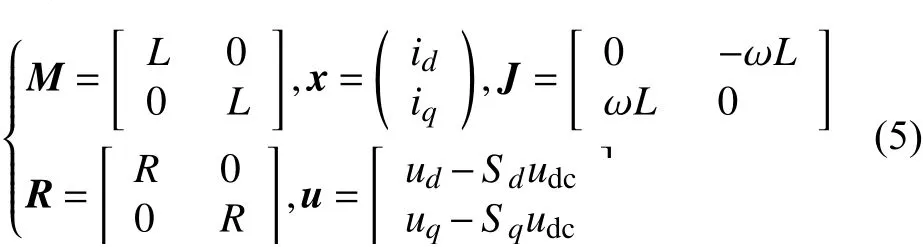
2.1.2 变流器无源性

对于多输入多输出系统：

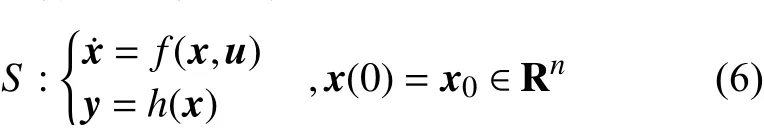
式中：x∈Rn;u∈Rn为输入；y∈Rm为关于x连续的输出；f为关于(x,u)局部Lipschitz的函数。

对于系统S，若存在半正定能量存储函数H(x)及半正定函数Q(x)，对 ∀T>0使得耗散不等式：

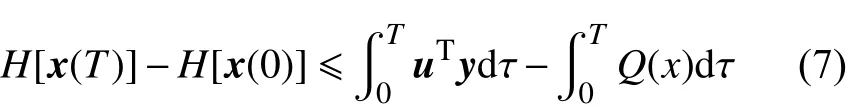
或者：

对系统的输入u、输出y及能量供给率uTy成立，则系统是严格无源的。

对于QZSC-SMES变流器系统，设系统的存储能量函数H=(1/2)xTMx，由式(4)可以得到：

令y=x、Q(x)=xTRx，满足式(8)，可知系统是严格无源的。

2.1.3 变流器无源控制器的设计

设系统期望平衡点：

系统交流侧的控制目标是使变流器能够准确地跟踪电网发出的有功、无功功率指令，电网有功、无功功率在系统期望平衡点的公式为

根据式(11)可以解得系统的期望平衡点表达式为

设系统误差存储函数He=(1/2)xTeMxe，其中误差变量xe=x−x∗。为使系统快速收敛到期望平衡点，使误差能量函数快速变为0，需注入阻尼，加速系统的能量耗散[15]。

设注入阻尼耗散项为

其中Ra为正定对角矩阵。则根据式(4)可得：

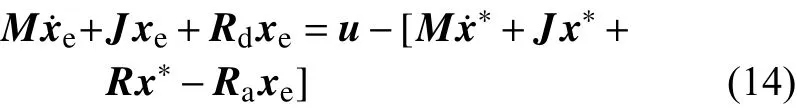
选取控制规律：

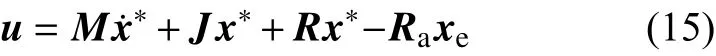
取Ra=diag(ra,ra)，联立式(5)、(10)、(15)可得到变流器开关控制方程为

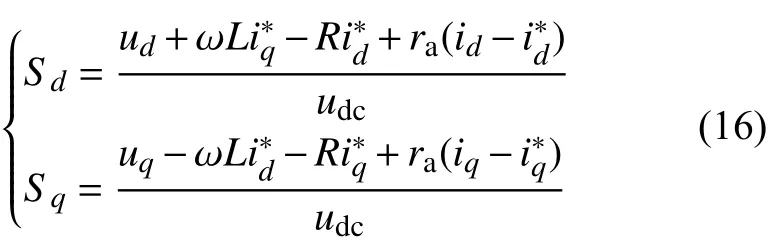
2.2 直流侧控制策略

2.2.1 斩波器数学模型

直流斩波电路通过控制全控开关管来控制超导磁体的充放电。通过分析斩波器充放电等效电路来建立斩波器在一个充放电周期内的数学模型，运用无源控制算法来控制直流电压。

斩波电路如附图A4所示，由2个全控型开关和2个二极管组成。根据系统工作模式的不同，将斩波电路分为充放电来进行分析。

如附图A5所示，当系统处于充电模式时，开关管S2、S3导通，此时系统对超导线圈进行充电，续流时，S3断开，二极管D1导通形成环路进行续流。如附图A6所示，当系统处于放电模时，S2、S3均关闭，二极管D1、D2导通，此时超导线圈对直流电容进行放电，来响应系统频率需求。续流时，开关管S3导通，与二极管D2形成续流电路。

设开关管S3的直通占空比为D，当超导线圈充电时，运用基尔霍夫定律可得斩波器的数学模型为

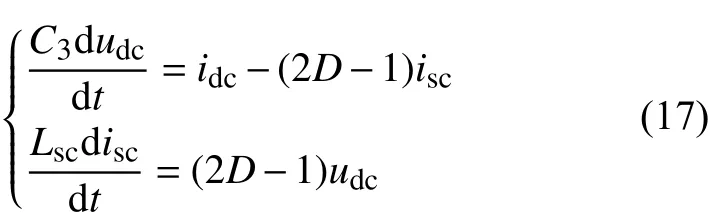
将式(17)写成无源控制的E-L方程：

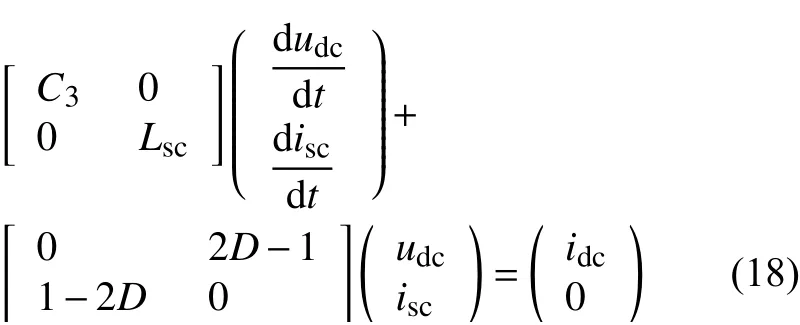
则E-L方程中：

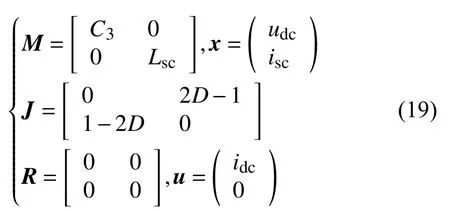
2.2.2 斩波器无源性

对于直流侧斩波器，设系统的存储能量函数H=(1/2)xTMx，由式(4)可以得到：

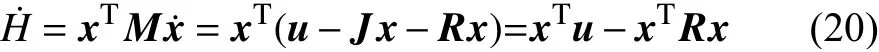
令y=x、Q(x)=xTRx，满足式(8)，可知系统是严格无源的。

2.2.3 斩波器无源控制器设计

斩波器的控制目的是通过控制跟踪直流侧电容电压，从而实现磁体功率的控制。设系统期望平衡点处斩波器状态变量

设系统误差存储函数He=(1/2)xeTMxe，其中误差变量xe=x−x∗。设注入阻尼耗散项为Rdxe=(R+Ra)xe，则根据式(4)可得：

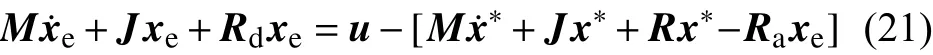
同变流器无源控制一样，选取控制规律：

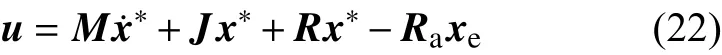
取Ra=diag(r1,r2)，联立式(19)(22)，可得：

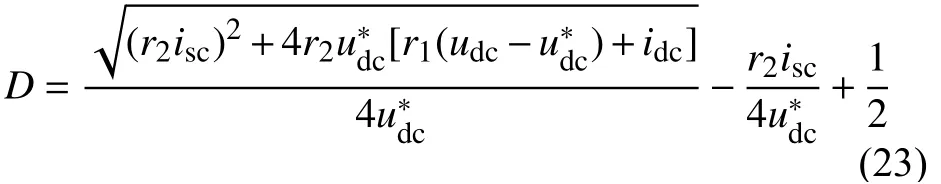
式(23)给出了斩波器的无源控制表达式，D为斩波器开关管S3的占空比表达式，在控制系统中，将占空比通过PWM调制即可得到开关管S2、S3的驱动信号。

图2给出了准Z源超导储能系统直流侧和交流侧的无源控制框图，其中变流器开关管的驱动信号由无源控制输出控制信号Sd和Sq经坐标变换后通过SVPWM调制得到，准Z源网络全控开关S1的驱动信号由SVPWM输出信号通过与非逻辑控制得到。斩波器全控开关S2、S3由无源控制输出占空比经PWM调制得到，从而实现直流侧电容电压的稳定以及相应系统功率指令对超导线圈的充放电进行控制。

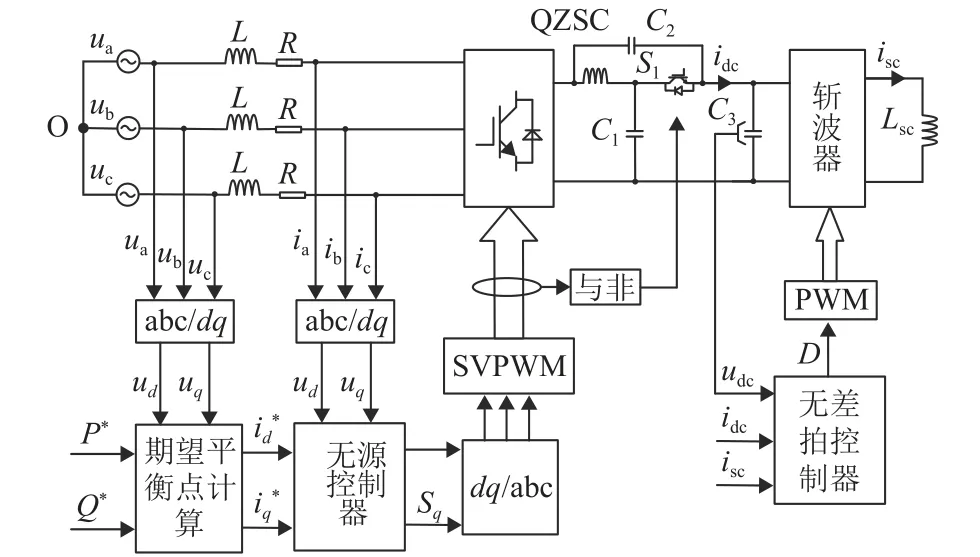
图2 系统控制框图Fig.2 Block diagram of system control

3 算例仿真

3.1 仿真参数

为了验证本文所提出的基于无源控制的准Z源SMES系统的控制的有效性，本文通过MATLAB/Simulink对整个系统各个控制模块进行了搭建。设置电网相电压有效值为220 V，频率为50 Hz；交流侧线路等效电感、电阻分别为2 mH和0.1Ω；准Z源网络电容C1=C2=40 mF，电感L1=L2=3 mH；直流侧稳压电容C3=4 mF，直流侧参考电压为1200 V；超导磁体电感Lsc=5H，初始电流150 A。

在用无源控制策略对交流侧进行控制时，需要校正阻尼系数ra，在设计无源控制器时，可通过逐步增加阻尼系数来进行取值。

附图A7分别为阻尼系数为50、100、150Ω时，有功电流id的波形，分析图A7可知当ra=50Ω时，有功电流存在明显的波动，当ra=100Ω时，有功电流的响应速度加快，波动显著改善，当ra=150 Ω时，波动进一步减小，根据参考文献[19]可知，阻尼注入的最大值为2L/Ts，其中L为交流侧电感值，Ts为载波周期，文中取L=1 mH，Ts=1×10−5s，因此交流侧无源控制器阻尼系数最大为200Ω，本文取150Ω。

斩波器无源控制器需要校正阻尼系数r1、r2，为使式(23)有解，需满足：

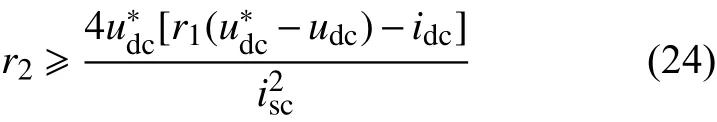
根据仿真实验要求，文中=1200 V，udc=0 V，idc=−600 A，isc=300 A，则根据式(24)可知：

仿真发现，当r1一定时，r2的取值对直流侧电容电压响应无显著的影响，分别取r1为200、400、600、800Ω，直流侧电压指令为1200 V时的电压响应波形如附图A8所示，由附图A8可知当r1从200 Ω到600Ω时，电压响应的稳态误差显著减小，当r1从600Ω增大到800Ω时，可以发现斩波器的控制效果无显著差别，综上，本文取r1=600Ω。

3.2 仿真算例

3.2.1 算例1

为验证本文所提出的双向准Z源变流器相对于传统Z源变流器的优势，分别搭建了Z源和准Z源SMES系统，在仿真中对2个系统均设置随时间t变化的有功功率指令，分别在0 s、0.2 s和0.4 s时刻给系统发出100 kW、200 kW和−100 kW的有功功率指令。无功功率设置为0 kV·A。

图3给出了在无源控制下Z源和准Z源变流器直流侧输入电流，从图中可以明显看出相比于传统Z源变流器，使用准Z源变流器的SMES系统直流侧输入电流更连续，从而简化了滤波电路。

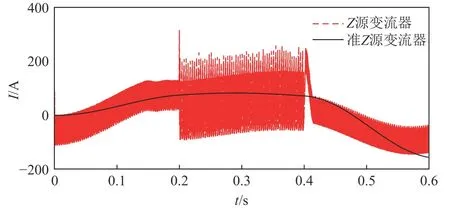
图3 Z源和准Z源变流器直流侧输入电流波形Fig.3 DC side input current waveformsof Z-sourceand quasi-Z-source converter

3.2.2 算例2

为验证本文所提QZSC-SMES交流侧无源理论的有效性，在仿真中对QZSC-SMES系统设置随时间t变化的有功功率指令，分别在0 s、0.2 s和0.4 s时刻给系统发出100 kW、200 kW和−100 kW的有功功率指令。无功功率设置为0 kV·A。

图4给出了传统PI控制和无源控制下准Z源超导储能系统交流侧变流器实际响应时的有功功率和无功功率随时间t变化的波形。由图4可知本文提出的交流侧无源控制器可以快速无超调的精确跟踪给定的功率指令，有效克服了传统PI控制器超调大的缺点，动态性能表现优异。可以看出所提出的无源控制策略在对有功无功进行独立控制时，相比于传统PI控制需要整定内外环PI参数，无源控制简化了系统的设计，且具有更好的控制效果。

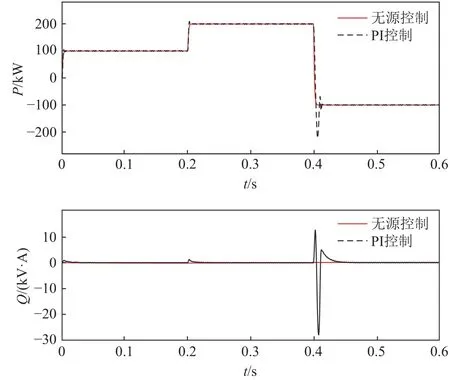
图4 变流器交流侧功率响应Fig.4 Power response of AC-sideconverter

图5(a)、图5(b)分别为无源控制和传统PI控制下准Z源变流器交流侧A相的相电压和相电流的波形图。取0.2～0.4 s的A相相电流进行快速傅里叶分析，得到如图6所示的分别在无源控制和传统PI控制下交流侧电流的总谐波失真(total harmonic distortion，THD)对比图。

如图6所示，无源控制时交流侧电流的THD为0.25%，相比于传统PI控制时的1.15%有了明显的降低，根据图5的A相电流波形对比也可以看出，本文所提出的无源控制有效改善了QZSCSMES系统输出的电能质量。

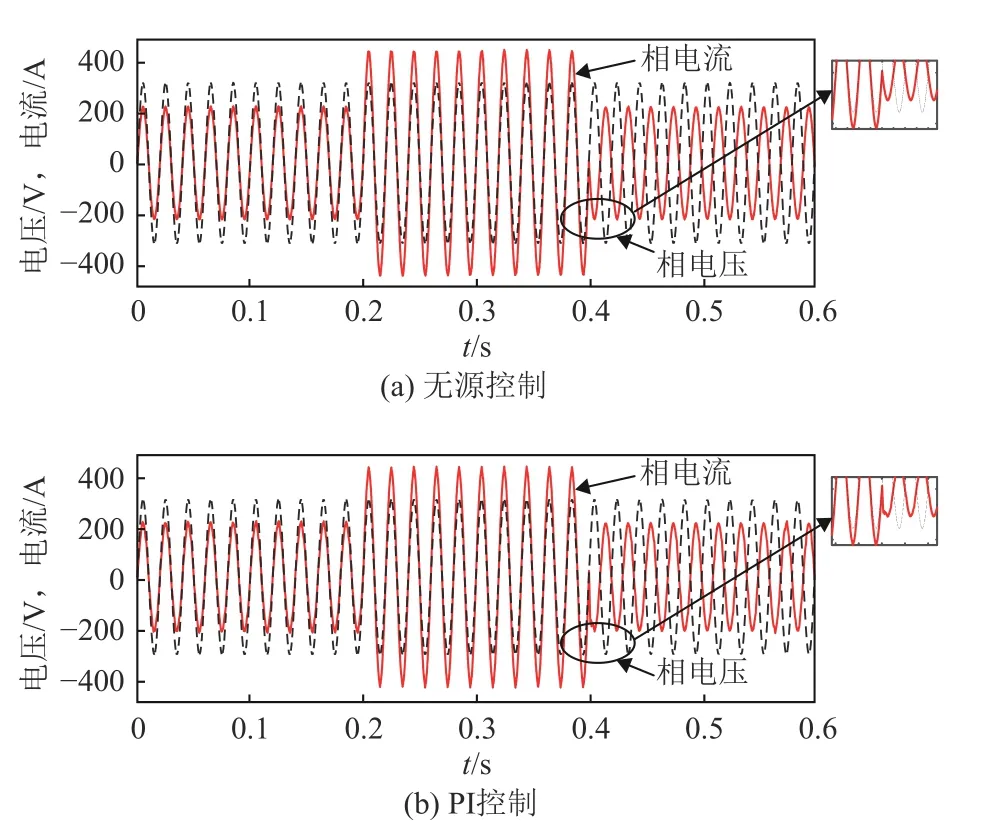
图5 交流侧A相相电压、相电流波形Fig.5 Phase voltage and phase current waveforms of phase A at AC side

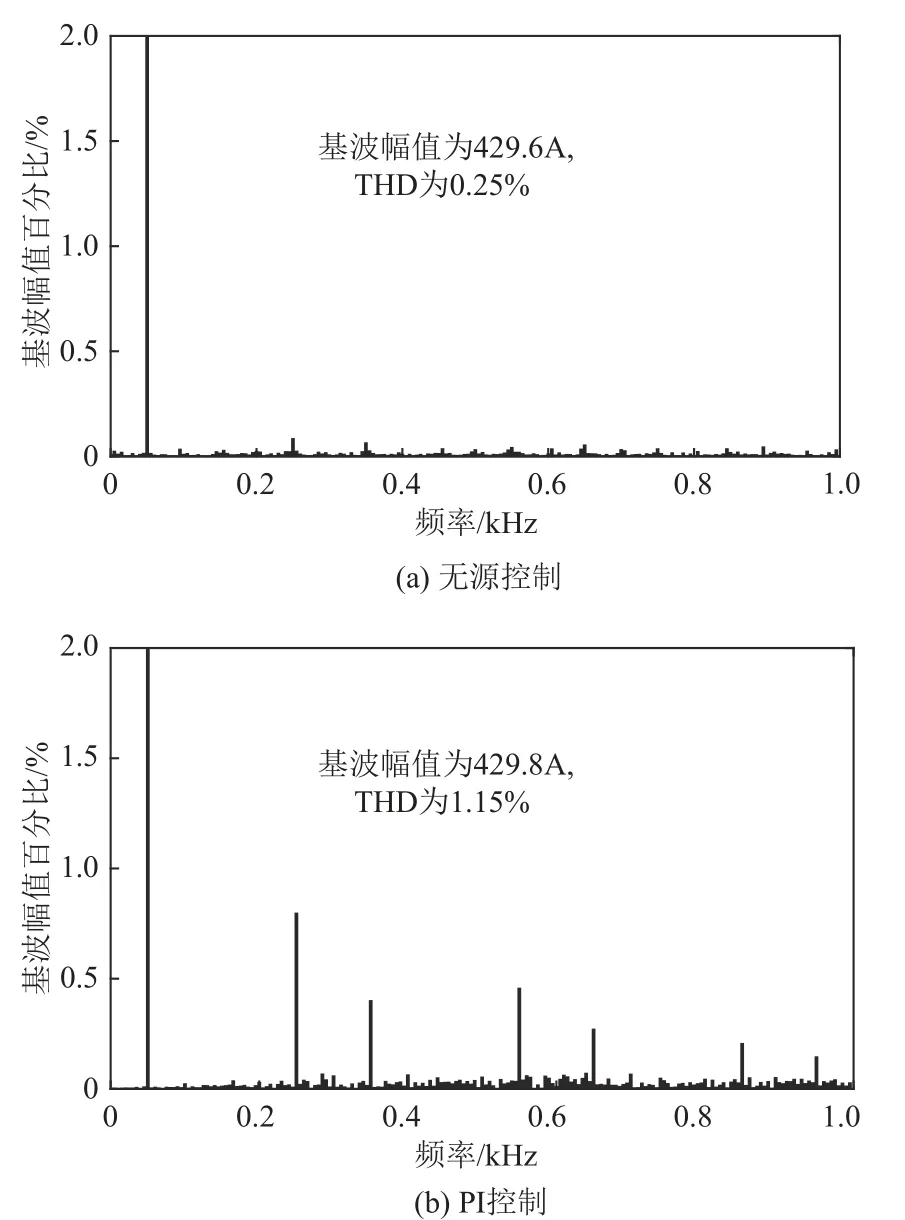
图6 2种控制策略下相电流THD对比Fig.6 Comparison of THD of phase current under two control strategies

为了验证本文对于QZSC-SMES系统直流侧所提无源控制理论的有效性，对比了分别在传统PI控制和无控制下直流侧电容电压随时间变化的波形。如图7所示，无源控制对于直流侧电容电压给定值能够精确稳定的跟踪，而传统PI控制则在系统功率指令发生变化时，有较大的波动。通过对比可以验证本文对于直流侧提出的无源控制策略具有有效性。

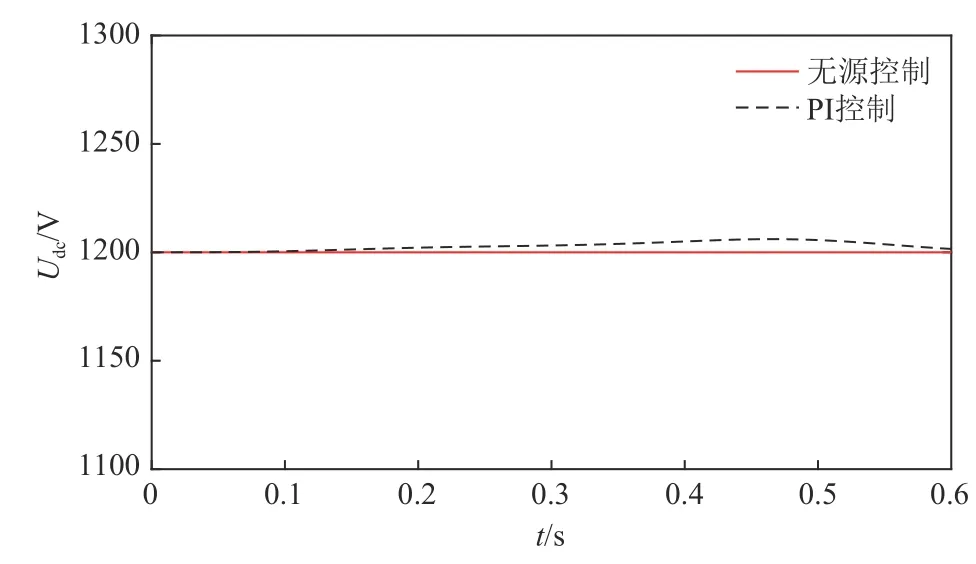
图7 直流侧电容电压波形Fig.7 Waveform of capacitor voltage at DC side

3.2.3 算例3

为了验证本文所提出的基于无源控制理论的QZSC-SMES系统的有效性，在算例2中将本系统应用于平滑风电场并网功率的波动。附图A9为风电原始功率，设置系统并网功率为21 kW。图8为在不同控制策略下，经过QSC-SMES系统平滑后风电并网功率。附图A10为PI控制和无源控制下SMES吸收的有功功率曲线以及SMES吸收功率的参考值曲线。

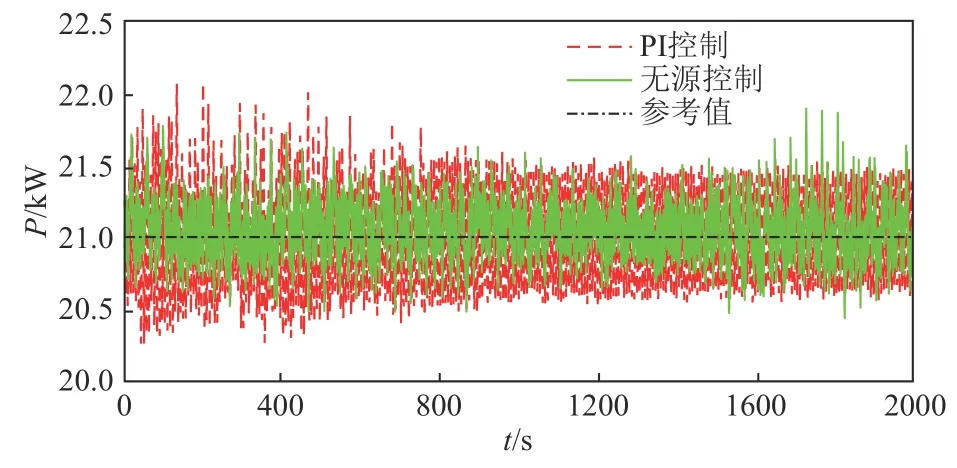
图8 2种控制策略下经QZSC-SMES平滑后的并网功率Fig.8 Grid-connected power smoothed by QZSC-SMES under two control strategies

由图8可知，传统PI控制和无源控制均可以实现系统对风电功率波动的平抑，但与PI控制对比，无源控制下的功率波动更小，能够对功率指令快速准确的跟踪，平抑风电功率波动的效果更好。

4 结论

为了改善传统SMES变流器在实际应用中的一系列问题，本文提出了基于双向准Z源变流器新型拓扑结构的SMES系统，并研究了其基于无源控制器的控制策略，得出以下结论：

1）基于双向准Z源变流器的SMES系统可以有效解决桥臂上下开关易受干扰造成直通损坏的问题，使系统直流侧输入电流更连续，验证了新型双向准Z源变流器应用于SMES系统的有效性；

2）所提出的变流器交流侧无源控制策略可以提高系统的动态响应，改善系统输出的电能质量，所提直流侧无源控制策略能够准确地控制磁体对系统功率指令的响应，并实现了对直流侧电容电压的稳定控制；

3）将本文所提出的QZSC-SMES系统应用于风电并网系统中，能够实现系统对功率指令的快速响应，有效平滑了风电并网功率的波动。

（本刊附录请见网络版，印刷版略）

附录A

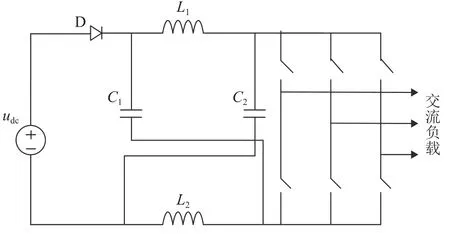
图A1 Z源逆变器拓扑图Fig.A1 Topology of Z sourceinverter

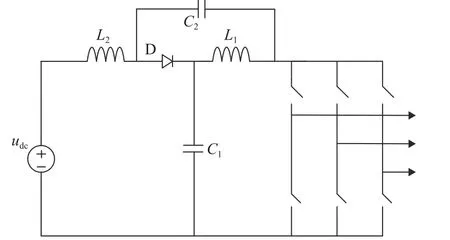
图A2 准Z源逆变器拓扑图Fig.A2 Topology of quasi-Z sourceinverter

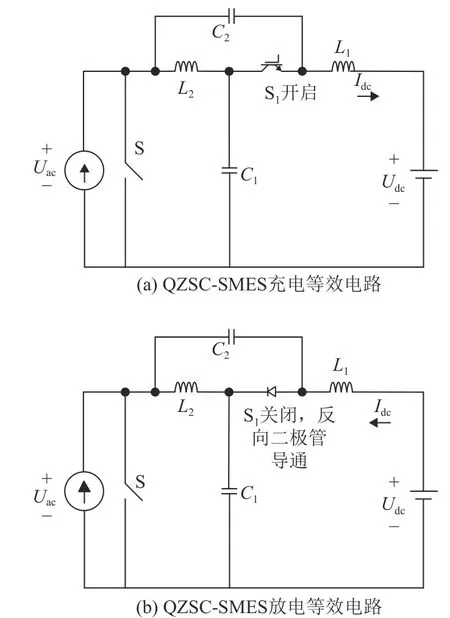
图A3 QZSC-SMES等效电路Fig.A3 Equivalent circuit of QZSC-SMES

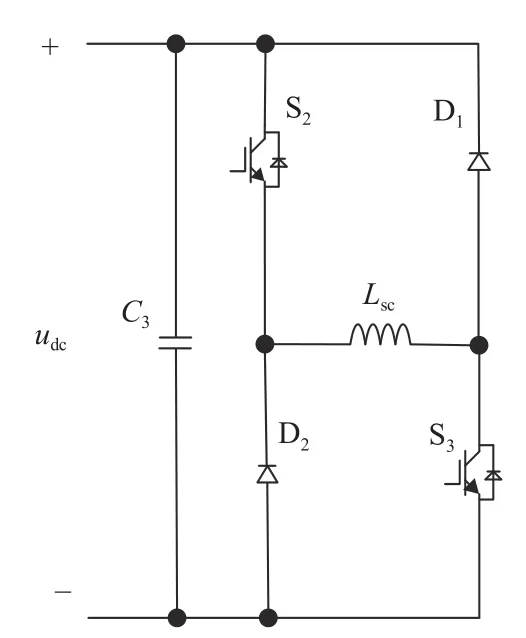
图A4 直流侧斩波电路Fig.A4 Chopper circuit at DC side

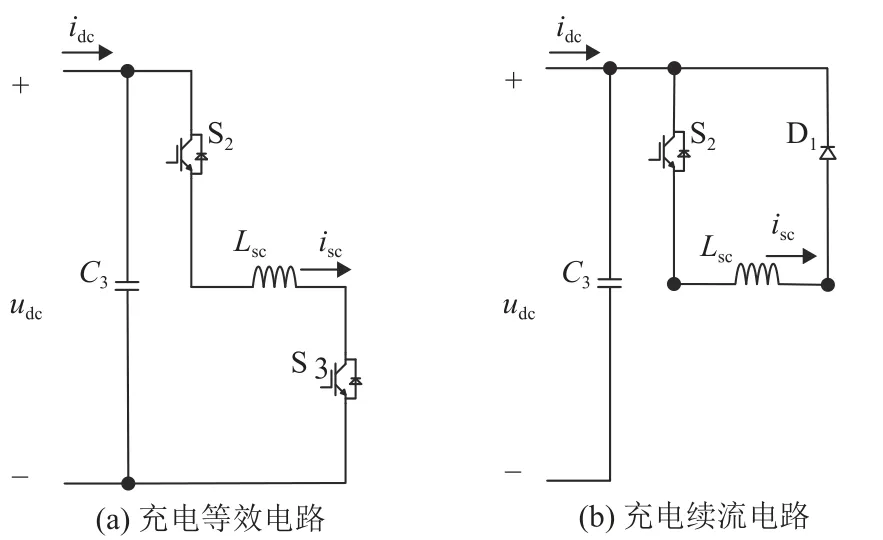
图A5 充电模式Fig.A5 Charging mode

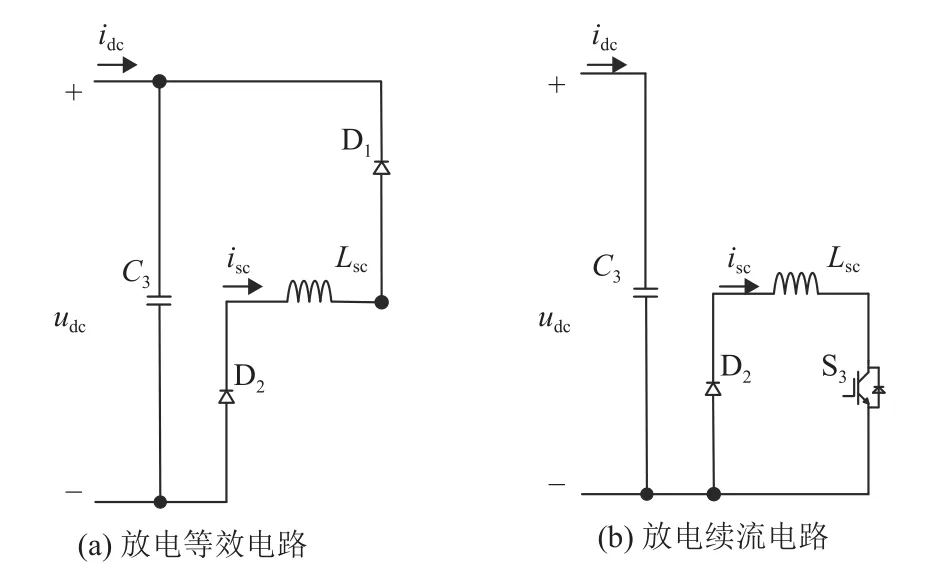
图A6 放电模式Fig.A6 Dischargemode

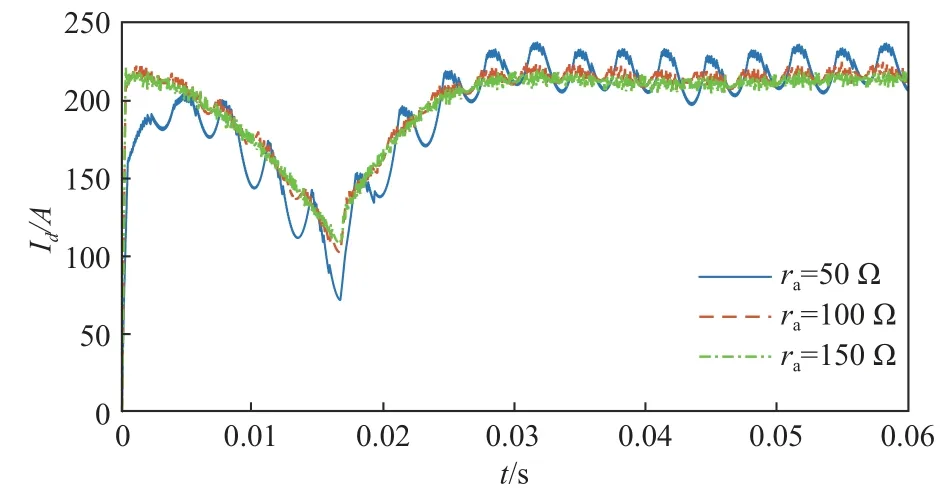
图A7 不同阻尼系数下d轴电流波形Fig.A7 Waveform of d-axiscurrent under different damping coefficients

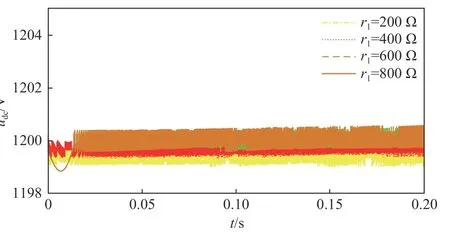
图A8 不同阻尼系数下直流电压波形Fig.A8 DC voltage waveform under different damping coefficients

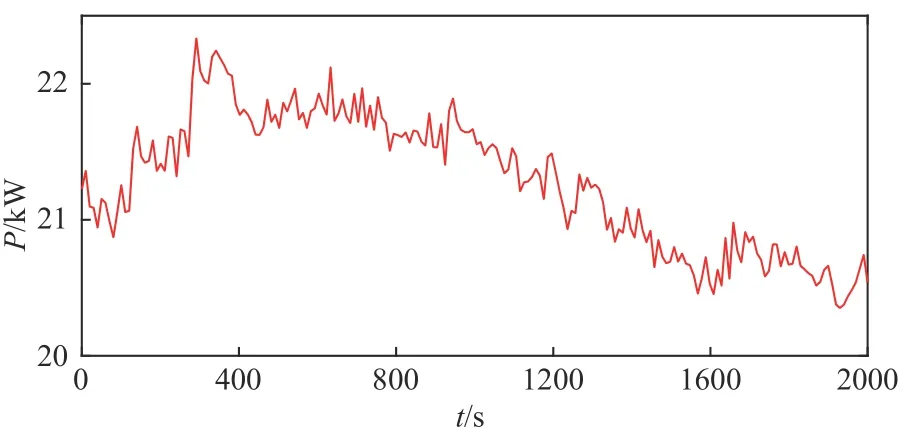
图A9 原始风电功率Fig.A9 Original wind power

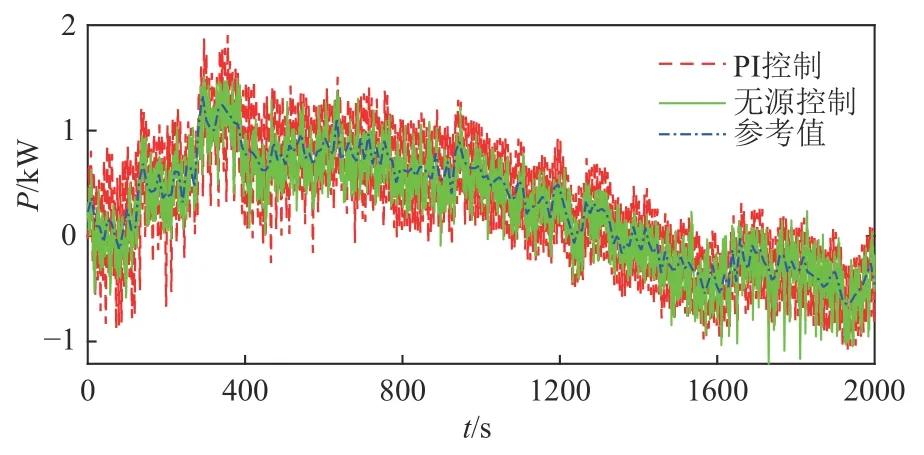
图A10 2种控制策略下SMES吸收的有功功率Fig.A10 Active power absorbed by SMESunder two control strategies