基于密度泛函理论的CO2对NO异相还原影响的机理研究

周 赛 ，刘 虎 ， 于鹏飞 ，车得福

（西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049）

NOx是燃煤电站排放的主要污染物之一，是形成酸雨和光化学烟雾的重要前驱物，且能够促进空气中二次颗粒物的形成，加剧雾霾天气发生[1]。煤粉锅炉燃烧过程生成的NOx中95%左右为NO，因此，深入了解燃烧过程中NO的还原机理对火电厂和环境保护具有重要意义。

NO可以通过与HCN、CO和烃基的均相反应或与焦炭的异相反应来还原。研究表明，NO的异相还原，是再燃技术以及低NOx燃烧器等去除NO 的主要机制[2 − 4]。世界各国已经有很多学者致力于研究煤焦对 NO 的异相还原机理[5 − 7]，并得出以下结论：

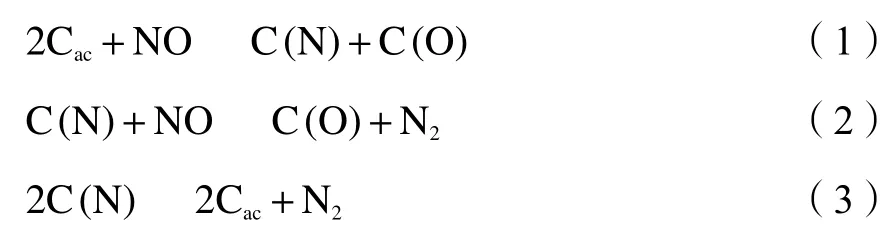
式中，式（2）和式（3）为竞争关系，Cac代表焦炭表面的碳活性位点，C(N)和C(O)分别代表焦炭表面碳氮组分和表面碳氧组分。

但是，在实际的燃烧条件下，NO的异相还原机理将发生较大改变。CO2作为煤燃烧最主要的产物，在常规空气燃烧后期，其体积分数可达到14%−16%，将会对NO异相还原反应产生显著的影响[8, 9]。CO2对焦炭-NO反应的影响规律已经有不少学者进行了实验研究，Liao 等[10 − 12]均在悬浮床反应器中分别进行了N2和CO2气氛下的煤焦-NO异相还原实验，发现CO2气氛下的NO还原率更低，即高含量的CO2会抑制NO被煤焦有效还原，他们将这种抑制作用归因于CO2抢占NO的碳活性位。除高含量CO2的抑制作用外，Aarna等[13, 14]还发现添加2%的CO2对NO-焦炭反应几乎无影响。相反的，吕刚等[15]则在900 ℃条件下研究了不同CO2体积分数（0−30%）对煤焦还原NO的影响，结果表明，CO2体积分数的提高有利于NO-焦炭的反应。Zhao等[9]进一步发现，较低体积分数的CO2(< 5%)可使NO还原率提高5%−16%，而高体积分数的CO2对NO异相还原作用影响不大。两位学者均将促进作用归因于CO2气化生成大量CO，CO进而促进煤焦-NO反应。张永春等[16]的实验则发现高体积分数CO2对NO-煤焦反应存在明显的双温区效应，即当反应温度低于770 ℃时，具有一定的促进作用，当温度高于770 ℃时，则呈现出抑制作用。此外，他们还发现，高体积分数CO2气氛下，虽然反应过程中生成了大量CO，但其并未对煤焦-NO还原反应起到明显的促进作用。

综上，对于CO2对焦炭-NO还原反应的影响，目前仍没有统一的结论。虽然众多学者进行了单独CO2气氛下的煤焦-NO异相还原实验，但由于CO2的气化反应与NO的异相还原反应同时进行，致使CO和CO2在反应过程中同时存在，不能完全分离。因此，目前CO2对NO-焦炭反应影响的实验研究，将促进作用都归因于CO，而对于CO2的直接影响仍不清楚。

近年来，量子化学在燃烧领域的应用越来越广泛，使得对燃烧过程中反应机理的理解提高到了分子水平。Kyotani等[17]首次利用从头算理论分析了不同焦炭模型与NO/N2O的反应特性，Montoya等[18]利用密度泛函理论研究了焦炭氮与NO 反应生成 N2和 N2O 的反应机理，Sendt等[19 − 21]同样利用密度泛函理论阐述了O2与焦炭的反应机理，都与实验取得了良好的一致性。对于焦炭-NO-CO2反应的量子化学研究，目前，主要集中于CO2在焦炭表面的吸附以及后续的气化反应，缺少对于CO2直接影响焦炭-NO反应的研究。Montoya等[22, 23]对CO2在炭质表面的吸附进行了系统的分子模拟研究，发现CO2吸附后可以形成内酯、杂环和呋喃三种稳定络合物结构，随后C−O键易发生解离生成CO和表面C(O)络合物，加深了对CO2气化的理解。此外，他们还发现三种结构中内酯最稳定，放热性最强，这与Roberts等[24]的研究结果相同。Zhu等[25]用密度泛函理论研究了CO2对炭气化的影响，发现CO2的化学吸附仅发生在两个连续的边缘活性位点上。

综上所述，由于实验研究的局限性以及气固反应的复杂性，目前，CO2对NO-焦炭反应的直接影响仍然不够清楚。本研究的主要目的是利用密度泛函理论探究CO2对NO异相还原影响的反应机理，明确CO2对该反应的影响，以加深对燃烧过程中NO异相还原的理解，最终实现燃烧过程中调控NO生成，这对NOx生成控制具有重要意义。

1 计算理论

1.1 模型选择

合理的焦炭模型是保证计算结果准确的重要因素。研究表明，单层石墨烯结构是量子化学中良好的炭基模型，Chen等[26]对不同数量苯环的石墨模型进行分析比较，发现六个及以上苯环组成的石墨模型可以很好的模拟焦炭。Kyotani等[17]发现使用具有armchair结构的模型模拟焦炭-NO的异相还原反应，结果与实验结果比较相符。因此，本研究选用具有四个活性位点的六环armchair模型模拟焦炭[27 − 29]，进行煤焦-NO 异相还原的计算。使用氢原子封闭模型边缘的碳原子来减弱边界效应，其中，上部边缘的碳原子去除氢原子来模拟活性位点[26]。具体模型结构如图1所示。

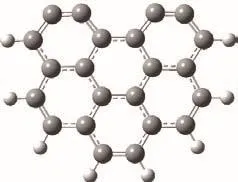
图1 Armchair焦炭模型Figure 1 Armchair edge model

1.2 理论方法

计算精度和耗时受到计算方法和基组的严重影响。研究表明，B3LYP/6-31G(d)方法[30]不仅可以在合理的成本下得到满意的结果，而且模拟焦炭 时 自 旋 污 染 小[18, 19, 31, 32]。 同 时 ， 为 了 弥 补 B3LYP在描述色散力方面的不足，本文加入DFT-D3色散校正[33]。因此，用B3LYP-D3/6-31G(d)计算级别对各驻点结构进行几何优化和频率分析。B3LYPD3/def2-TZVP级别对能量的计算更加精确，用于计算反应路径中涉及到的所有能量[34]。电子基态的确定是通过对不同自旋多重度下的结构能量进行计算，并用零点能校正后的吉布斯自由能计算基元反应的能垒，得到整个反应的势能面。内禀反应坐标（IRC）[35]计算用于对过渡态的合理性进行确定。本文量子化学计算均利用Gaussian09[36]软件完成。

根据经典过渡态理论（conventional transition state theory，cTST），反应速率常数计算公式[37]如下：

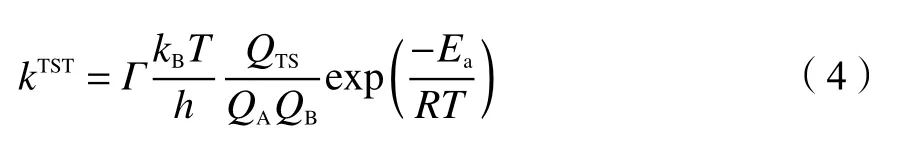
式中，Г为量子隧道修正系数；Ea为反应势垒，kJ/mol；R为气体摩尔常数，J/（mol·K）；T为温度，K；kB为玻尔兹曼常数，J/K；h为普朗克常数，J·s；QTS、QA、QB依次为过渡态TS和反应物A和反应物B的配分函数。

式中，vm为反应路径振动的虚频值，cm−1；c为光速，m/s。

2 结果与讨论

2.1 煤焦-NO异相还原反应

图2给出了煤焦-NO异相还原反应路径的势能面，图3给出了反应路径中涉及的各驻点结构及部分键长数据，其中，“R”代表反应物，“IM”代表中间体，“TS”代表过渡态，“P”代表产物。为便于描述，对图3中的相关原子进行编号。

图2 煤焦-NO 异相还原路径的反应势能面Figure 2 Potential energy surface of NO heterogeneous reduction

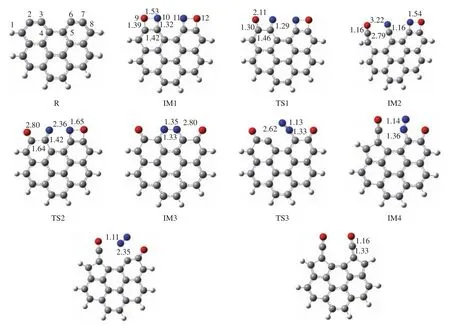
图3 煤焦-NO 异相还原反应的各驻点结构（键长：Å）Figure 3 Structures of stagnation points of NO heterogeneous reduction (bond length: Å)

首先，两个NO分子分别占据两个活性位点，以side-on模式吸附在焦炭边缘，生成具有两个四元环的中间体IM1。此吸附过程无需翻越任何能垒，并释放出405.4 kJ/mol的热量，这与Kyotani等[17]和张秀霞[5]的研究结果相符。其中，N10−O9键由NO 的 1.16 Å伸长到 1.53 Å，这表明随着 C−N、C−O化学键的形成，N−O键有断裂的倾向。IM1克服73.4 kJ/mol（TS1）的能垒将 N10−O9 键和 C2−C3 键破坏，得到中间体IM2，该过程放出169.4 kJ/mol的热量。TS1 有且只有一个虚频 692.14 cm−1，其振动方向是O9和N10原子分别向纸面外和纸面内相互远离。IRC能量路径表明，N−O键断裂的同时，C2和 O9原子靠近（1.39 Å→1.30 Å→1.16 Å）、C3和 N10原子靠近（1.32 Å→1.29 Å→1.16 Å）以及C2−C3 之间的距离增加（1.42 Å→1.46 Å→2.79 Å）。第二个N−O键（即N11−O12键）的断裂需要克服171.7 kJ/mol（TS2） 的 能垒，并放 热 271.3 kJ/mol。TS2 同样只有一个虚频 230.35 cm−1，其振动方向为N11原子和O12原子的远离，导致N11−O12键断开。在该反应过程中，C2和C3原子重新成键形成苯环（2.79 Å→1.64 Å→1.51 Å），N10 和 N11 原子成键形成六元环结构IM3。C3−N10键的键长也由 IM2结构的 1.16 Å伸长至 IM3结构的 1.33 Å。C3−N10键的伸长有利于该键的断裂，同时N−N键得到增强（1.35 Å→1.14 Å）。过渡态 TS3有且只有一个虚频 289.86 cm−1，其振动方向是 C3 和 N10原子相互远离，直至断裂，进而导致C3原子靠近C1原子，最终C1−C2键断裂，C1和C3原子成键，生成具有五元环的IM4结构，此过程需翻越297.0 kJ/mol的能垒，并吸收 41.5 kJ/mol的热量。随后，C6−N11键被增强的N−N键削弱直至断裂，C6和N11原子的远离同样导致C6和C8原子的靠近，最终 C7−C8键断裂，C6−C8键形成，生成具有两个五元环的产物P1结构。该过程需克服147.5 kJ/mol（TS4）的能垒，并放出 49.3 kJ/mol的热量，TS4 仅有的一个虚频为 152.11 cm−1。综上，该反应的总体表达式为：Cac+2NO→P1+N2，整个反应为放热反应，共放出853.9 kJ/mol的热量，最高能垒为 297.0 kJ/mol。Sendt和 Haynes的研究表明，N2从焦炭表面脱附后，CO很容易克服焦炭表面碳原子的束缚释放出来，使C3和C6成为新的活性位点[19 − 21]。

2.2 CO2参与煤焦-NO异相还原反应

2.2.1 CO2在Armchair型焦炭表面的吸附构型

CO2分子可以以两种不同的方式吸附在armchair结构焦炭表面：C−O−down模式和 O−O−down模式。由于armchair结构焦炭边缘不同的碳位点常表现出不同的活性[29, 38]，因此，首先对 CO2以不同方式吸附在armchair结构焦炭表面时生成的构型进行计算。吸附构型与能量变化如图4所示。由图4可知，CO2在armchair结构焦炭表面的吸附有四种构型。由能量变化可知，当CO2以C−O−down的方式吸附在armchair型焦炭表面的边缘C3和C6活性位点上释放出的能量最多，即Z1结构（内酯）最容易形成且最稳定。因此，本研究在关于CO2参与煤焦-NO异相还原反应路径研究中，均采用吸附构型Z1作为反应的起始反应物。

图4 CO2 吸附构型与能量Figure 4 Adsorption configuration and energy of CO2

2.2.2 CO2参与煤焦-NO异相还原反应

图5给出了CO2参与煤焦-NO异相还原反应路径的势能面，图6给出了反应路径中涉及的各驻点结构及部分键长数据。为便于描述，对图6中的相关原子进行编号。

图5 CO2 参与 NO 异相还原路径的反应势能面Figure 5 Potential energy surface of NO heterogeneous reduction with the participation of CO2

图6 CO2 参与 NO 异相还原反应的各驻点结构（键长：Å）Figure 6 Structures of stagnation points of NO heterogeneous reduction with the participation of CO2 (bond length: Å)

首先，CO2以C−O−down的方式吸附在焦炭边缘的C3和C6活性位点上，形成具有内酯结构的中间体IM1，并释放出191.1 kJ/mol的热量。在该吸附过程中，C11–O9键的键长由 CO2的 1.17 Å伸长至 1.40 Å，有断裂的倾向，这与 Montoya 等[22, 23]的研究结果相符。紧接着，第一个NO分子以N–down的方式吸附在C7活性位点上，生成中间体IM2，该过程同样是一个放热过程，释放出176.2 kJ/mol的热量。随后C11和O13之间的距离缩短，生成IM3，该过程克服 42.8 kJ/mol的能垒（TS1）。TS1 有且仅有一个虚频 168.07 cm−1，其振动方向为 N12−O13键的旋转。C11−O9键断裂需要克服162.1 kJ/mol的能垒（TS2）。过渡态 TS2 仅有的虚频为 936.63 cm−1。从TS2的振动方向分析，C11原子和O13原子有相互靠近的趋势。C11和O13之间的距离进一步缩短并成键，形成具有五元环结构的中间体IM4。随后，IM4发生开环反应，脱附出CO2，生成IM5结构。查看TS3虚频399.23 cm−1的振动方向，C11原子远离C6原子，直至C6−C11键断裂。N12−O13的键长也由1.38 Å伸长直至断裂，该过程是一个高能垒的过程，需克服214.1 kJ/mol的能垒。

第二个NO分子以N−N结合的方式吸附在中间体IM5表面生成含氮和氧的五元杂环结构IM6，并释放出 472.7 kJ/mol的热量。其中，N12−N14成键、C6−O15成键、N14−O15键由 1.16 Å伸长至1.47 Å，倾向于断裂。查看TS4唯一的虚频164.07 cm−1的振动方向，发现 N14 有远离 O15 原子的趋势。N14−O15键继续伸长至2.79 Å比较容易，同时 N12−N14 键长由 1.25 Å缩短至 1.19 Å，得到进一步增强，能垒仅为13.8 kJ/mol。最后是C7−N12键断裂脱附出N2分子，需要克服65.7 kJ/mol的能垒，并吸收29.7 kJ/mol的能量，生成产物P2。TS5 有且仅有一个虚频 370.80 cm−1，振动方向为C7原子和N12原子相互远离。综上，该反应的总体表达式为：Cac+CO2+2NO→P2+N2+CO2，整个反应为放热反应，共放出593.7 kJ/mol的热量，最高能垒为214.1 kJ/mol。同样，N2从焦炭表面脱附后，CO很容易克服焦炭表面碳原子的束缚释放出来。

2.3 热力学和动力学分析

通过对NO与煤焦异相还原的计算模拟可知，CO2分子参与下的煤焦-NO异相还原反应，在CO2脱附的过程中，最初吸附的CO2分子中的O9原子留在了焦炭表面，形成了表面C（O）络合物，剩余的表面羰基夺取了第一个吸附的NO分子中的O原子，形成新的CO2分子脱附出去，留下含有表面碳氮组分和表面碳氧组分的焦炭。CO2分子的脱附将表面碳氮组分邻近的C6原子活化，形成碳活性位点，这有利于后续NO的吸附以及N2的脱附。

对于无CO2参与反应的条件下，中间反应IM3→IM4 的能垒（297.0 kJ/mol）明显高于其他中间反应的能垒；对于CO2参与反应的条件下，中间反应 IM4→IM5+CO2的能垒（214.1 kJ/mol）明显高于其他中间反应的能垒。因此，IM3→IM4和IM4→IM5+CO2分别为两个反应的反应速率决定步。对比两个反应的能垒可以发现，CO2参与条件下的最高能垒明显于无CO2参与条件下的最高能垒。从热力学角度来看，CO2分子的参与降低了煤焦−NO反应的能垒，使得NO异相还原反应更容易进行。

为了加深对反应难易程度的理解，经典过渡态理论被用于上述两个决速步的反应速率常数的计算，如图7所示。由图7可以看出，反应速率常数均随着温度的升高而增大，说明提高温度对NO异相还原起到促进作用；通过对比无CO2分子参与的NO异相还原反应可以发现，在298.15−1800 K条件下，CO2分子参与条件下的决速步的反应速率常数恒大于无CO2分子参与的决速步的反应速率常数。拟合得到两个反应的动力学参数见表1。由表1可知，CO2分子参与条件下的决速步的活化能低于无CO2分子参与的决速步的活化能，即CO2分子降低了反应的活化能。动力学研究表明，CO2分子参与反应时的NO异相还原过程更容易发生，CO2分子对NO异相还原存在促进作用。

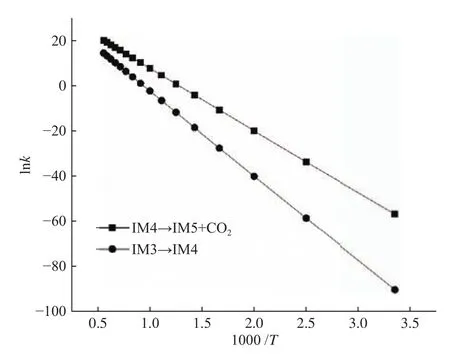
图7 经典过渡态理论得到的反应速率常数Figure 7 Rate constant k calculated from cTST

表1 拟合所得动力学反应参数Table 1 Fitted kinetic parameters of Arrhenius expressions

3 结 论

CO2能够在煤焦表面吸附，并且以C−O−down模式吸附在煤焦模型边缘形成的内酯结构最稳定，放热性最强。

在煤焦-NO异相还原过程中，吸附后的CO2分子中的C−O键易发生解离生成表面C（O）络合物和表面羰基。表面羰基夺取吸附态NO的O原子后脱附出CO2，为后续NO吸附及N2脱附提供邻近的碳活性位点。

热力学和动力学分析表明，与NO异相还原反应相比，CO2分子参与条件下的NO异相还原反应决速步能垒低，反应速率常数大。参与反应的CO2分子降低了该反应的最高能垒并且加快了反应速率。CO2对煤焦-NO异相还原反应具有促进作用。