从一道中考模拟题的评讲谈如何分层教学

江苏省南京市梅山第二中学 丁金华

本文从一道中考模拟题的讲解教学入手，以三问、变式为关键词，重点探讨如何开展初中数学分层教学。初中教师在指导复习阶段，尤其是在临近中考的复习过程中，要格外注重分层教学策略的应用，要通过这样一种方式去吸引不同类型、不同层次学生的注意力。

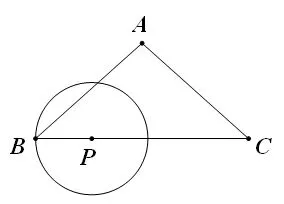
【例题】如图，在Rt △ABC中，∠ACB=90°，AC=6，BC=8，点P是BC的中点，动点Q从点P出发，沿射线PC方向以每秒2 个单位的速度运动，以点P为圆心，PQ长为半径作圆，设运动的时间为x（秒）。

（1）当x=1.2 时，判断直线AB与圆P的位置关系；

（2）当△APQ为等腰三角形时，求x；

（3）已知圆O为△ABC的外接圆，若圆P与圆O相切时，求x。

一、分层思路设置

这是一道典型的几何和代数相融合的题目，要求学生在解题时同时具有“数”“形”思维。而在针对这道题开启分层教学的过程中，要巧妙地设计各种解题变式，让不同的学生在解决变式的过程中都能够有所收获、有所进步。

二、分层教学实践

1.三问的具体求解过程

（1）问题（1）的解决

该问的题眼在于“判断直线AB与圆P的位置关系”，即判断直线和圆的位置关系，方法是求解圆心到直线的距离并同圆的半径来进行比较。因为P点是固定的，所以P点作为圆心和直线AB之间的距离是固定的，唯一的变动因素就在于点Q移动的过程中，会导致PQ距离的变化，也就是圆的半径大小存在变动因素。

当x=1.2 时，PQ的长度为2.4，也就是圆的半径，此时只需要比较2.4 与P点作为圆心的圆和直线AB之间的距离这两者的大小，即可求解第一问。

（2）问题（2）的解决

当△APQ为等腰三角形时，存在两种可能性：一是AP作为等腰三角形的底边，AQ=PQ；二是PQ是等腰三角形的底边，AP=AQ。需要分别针对这两种情况来进行讨论。

情况二：假设PQ是等腰三角形的底边，那么这道题根据等腰三角形原理，可以直接分析得出结论QC=PC=4，此时x的值也可以轻松求出。

（3）问题（3）的解决

关于这一问的求解，其实可以转换为当两个圆相切时，求另一个圆的半径。因为△ABC为直角三角形，所以根据定理可知，该三角形的斜边正好就是外接圆的直径，由此可以直接得出外接圆的半径为AB边的一半（根据勾股定理可知斜边长度为10，半径为5）。

通过图像不难发现，当圆O和圆P相切时，基于P点作BC的垂线，分别与圆O相较于两点，并形成了长、短两条线段，其中的短线段也就是相切时圆P的半径，如此就可以分析此时x的运动情况。

2.变式分层实践

为了让不同学生对类似的题目都能有所锻炼、有所提升，笔者在这道题目的基础上，另外引申出两道变式题目，拓展学生的学习层次：

变式一：在Rt △ABC中，∠ACB=90°，AC=6，BC=8，点P是BC上的动点，以点P为圆心，PC长为半径作圆，设PC为x，圆P截边AB截得的弦长为y。

（1）当圆P与直线AB相切时，求x；

（2）求y关于x的函数关系式并求定义域；

变式二：如下图，等腰三角形ABC中，AB=AC=10，BC=16，点P是BC上的动点，以点P为圆心，PB长为半径作圆，设PB为x，圆P截边AC截得的弦长为y。

（1）当圆P与直线AC相切时，求x；

（2）求y关于x的函数关系式并求定义域；

（3）当圆P经过点A时，求以AC为直径的圆O与圆P相交时两圆的公共弦长。

变式一的第一问和变式二的第一问可谓异曲同工，解题思路保持一致。

然后整理等式即可得出关于y关于x的函数关系式，并且根据y≥0 的客观要求，求解出定义域。

比较变式二和变式三，会发现两题的解题思路基本一致，只不过等腰三角形的解题条件要比直角三角形更为苛刻一些，这也是从难度上对两道题目提出分层的直接体现。

总而言之，围绕一道题目所开启的分层教学，归根结底是要考虑不同学生针对此类题目所能解决的不同程度、不同地步，在不同的位置获得分点。对于教师而言，更要培养学生不放弃题目，敢于从有限的题目中争取得分的意识。