基于互信息理论与递归神经网络的短期风速预测模型

王 岩，陈耀然，韩兆龙,b,c，周 岱,b,c, 包 艳,b,c

(上海交通大学 a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室；c.水动力学教育部重点实验室，上海 200240)

风能是一种清洁、经济的可再生能源.但是，风速的间歇性和波动性导致风力发电机的输出功率难以预测，进而为风电并网、能源输送和风电场制定交易计划等造成困难[1].开展风电场短期(未来1 h内)风速预测成为解决上述问题的关键[2].

目前，主要利用统计方法进行风电场的短期风速预测[3].该方法利用历史风速数据，建立历史风速与未来风速之间的统计模型而预测风速，具体方法包括时间序列和机器学习等[4].时间序列模型是线性统计模型，而风速序列模型是波动性和随机性较强的非线性统计模型，因此时间序列法预测风速的效果不佳[5].

机器学习是人工智能的一个分支，其在风速预测方面具有较强的非线性建模能力.人工神经网络(ANN)是典型的机器学习方法，其从信息处理的角度对人脑神经元网络进行抽象表达，进而建立非线性数学模型[6].Santhosh等[7]利用经验模态分解，将原始风速分解为多个子序列，并利用ANN分别对子序列进行建模预测.结果显示，相较于基于时间序列法的风速预测模型，基于ANN的模型的预测误差显著降低.支持向量机(SVM)作为另一种机器学习方法，其主要思想为先利用一个预设函数将原始输入和输出数据映射到高维特征空间，然后在该空间进行线性回归，使误差最小化.范曼萍等[8]利用SVM建立历史风速与未来风速之间的数学模型，并利用改进粒子群算法优化SVM的参数，通过收缩因子改进粒子速度更新方式.结果显示，基于SVM风速预测结果的平均相对误差为3.72%，预测精度显著提高.然而，ANN和SVM等传统机器学习方法模型仅将历史数据进行统一输入，而未充分考虑风速序列随时间的变化趋势，因此难以得到关于时间序列问题的高精度风速预测结果.

针对上述问题，提出一种风电场短期风速预测组合新模型，即基于互信息(MI)和递归神经网络(RNN)的短期风速预测模型(MI-RNN).将该模型应用于美国加利福尼亚州某风电场的2个风速数据集，进行数值实验，并与ANN和SVM进行比较分析，评价模型的预测精度.不同于上述机器学习方法，该模型中RNN加入t时刻的隐藏状态作为记忆单元，该隐藏状态中记录着t时刻的输出值，同时作为下一时刻的输入值，由此可以更有效地解决时间序列问题[9].该模型的创新点包括：①利用MI选择用于预测未来风速的历史风速长度，能够更有效地利用历史信息且无冗余数据，进而显著提高预测精度；②利用带记忆单元的RNN提取历史风速数据与未来风速之间的映射关系，历史信息提取能力更高.

1 理论方法

1.1 输入变量选择与MI理论

输入变量的选择对模型的预测能力有重要影响.针对建立的风速预测模型，给定历史风速序列(Ft-1,Ft-2, …,Ft-τ)，进行下一时刻风速(Ft)的预测，历史风速序列的长度(τ)由选择的输入变量决定.若τ太短，则历史数据中包含的信息太少，模型精度低；若τ太长，则模型参数优化困难且包含冗余历史信息，模型精度低且训练时间长.

MI理论能够衡量一个随机变量中包含另一个随机变量的信息量.假设2个随机变量(X1,Y1)的联合分布为p(x1,y1)，边缘分布为p(x1)和p(y1)，则互信息I(x1;y1)为联合分布和边缘分布的相对熵[10]：

(1)

1.2 递归神经网络

RNN是用于解决时间序列问题的机器学习模型，一个时间序列中的时间点对应一个普通前馈神经网络，并在每个时间点加入一个记忆单元记录其输出值，将输出值传递给下一时刻[11]，数学表达式为

ht=σ(UXt+Wht-1)

(2)

Ot=f(ht)

(3)

式中：h为状态值；σ(·)为状态激活函数；U为t时刻输入的权重；W为t-1时刻状态的权重；X和O为神经网络的输入值和输出值；f(·)为生成神经网络输出值的函数.

图1为τ=3的RNN模型图，时间序列中共包括3个时刻(t-1,t,t+1)的神经网络.本文将风速作为神经网络的输入值，Ot+1为RNN的最终预测值.每个时刻计算得到的隐藏层状态Ot-1均将传给下一时刻，从而保证前一时刻提取的历史信息可以传递到下一时刻.因此，图中Ot-1应为Xt的预测值，当采用每τ个风速预测一步时，则会产生τ个输出值，只保留最后一个输出值作为最终预测值.

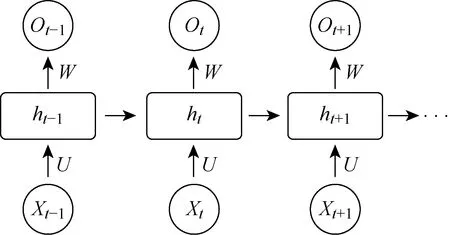
图1 RNN模型结构图

模型的训练过程即确定参数W和U的过程.训练过程的本质为优化，优化目标为缩小预测值与观测值的误差.利用误差函数对W和U求梯度，训练过程中逐渐降低梯度值至0附近，从而确定模型参数.然后，将历史数据输入到RNN中并输出最终预测结果.

2 MI-RNN模型

2.1 模型基本信息

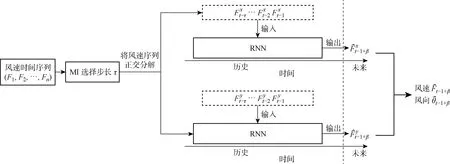
图2 MI-RNN流程图

为了实现带有风向的风电场风速预测，将风速数据进行正交分解：

(4)

式中：i=1, 2, …,t-1.然后使用MI-RNN模型预测t-1+β时刻的风速并进行组合：

(5)

2.2 基于MI理论选择时间步长

图3为I(τ)-τ变化曲线.其中，I(τ)为Ft和Ft-τ之间的互信息，是一个递减函数.可以通过选择互信息阈值(IC)来确定τ值大小.通常依据经验选择IC，本文选择IC=2，确定时间步长τ= 6.

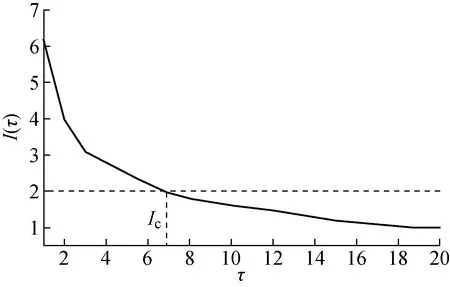
图3 I(τ)-τ曲线

2.3 RNN模型训练

将历史风速观测值数据以某时刻为界划分为训练集和测试集，训练集用于训练RNN模型，测试集用于测试模型的预测结果是否准确.当模型训练完成后，输入τ个新历史风速序列，RNN模型将输出新的风速预测值.

3 数值算例

3.1 算例1

为验证MI-RNN模型的性能，选择SVM和 ANN作为比较模型，讨论MI-RNN模型的风速预测精度.利用Adam优化算法进行模型训练，3个模型均使用scikit-learn机器学习库[12]和PyTorch框架[13].

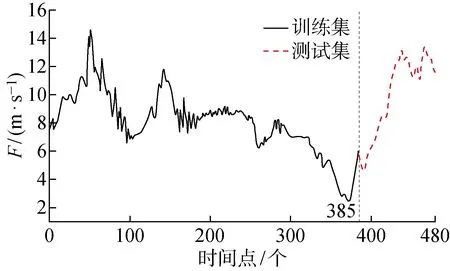
图4 观测间隔为15 min的风速数据集

3.1.2模型评估指标 模型评估指标能够评价模型预测结果的精度.分别利用均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2)对模型点预测结果进行统计.

RMSE和MAE用于描述预测值与观测值的误差情况，但区别在于：RMSE对预测值与观测值的偏差进行了一次平方，容易将误差放大[14]；R2用于评价风速预测模型的平均预测精度[15].公式如下：

(6)

(7)

(8)

式中：Te为总观测量.RMSE和MAE越接近0，R2越接近于1，则模型的预测精度越高.

3.1.3结果与讨论 为加强模型预测结果的可视化，对3个模型的预测和评估结果作图，如图5～8所示.

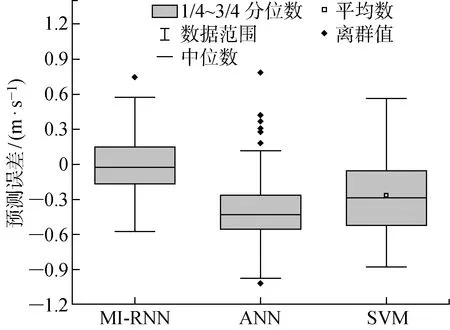
图5 预测误差统计

图5中，MI-RNN模型的预测误差平均值的绝对值最小(小于0.1 m/s)，SVM模型次之(约为 0.2 m/s)，ANN模型最大(大于0.3 m/s).3个模型预测误差的中位数和平均值相差较小，1/4～3/4分位数据范围的宽度相差较小(约为1.2 m/s).MI-RNN 和ANN模型的预测误差均有大于0的离群值，但MI-RNN模型的离群值较少.结果表明：与ANN和SVM模型相比，MI-RNN模型预测结果的平均误差最小，且离群值较少，预测精度更佳.

图6中，MI-RNN模型的预测值与观测值相差较小，且在风速小或大的情况下均能够精准预测.而ANN和SVM模型的预测值与观测值相差较大，存在明显预测误差.其中，SVM模型在风速较小时误差较大，在风速较大时误差更大；ANN模型在风速小或大时误差均较大.结果表明：与ANN和SVM模型相比，MI-RNN模型的预测精度更高，且在不同风速范围下的预测稳定性更佳.

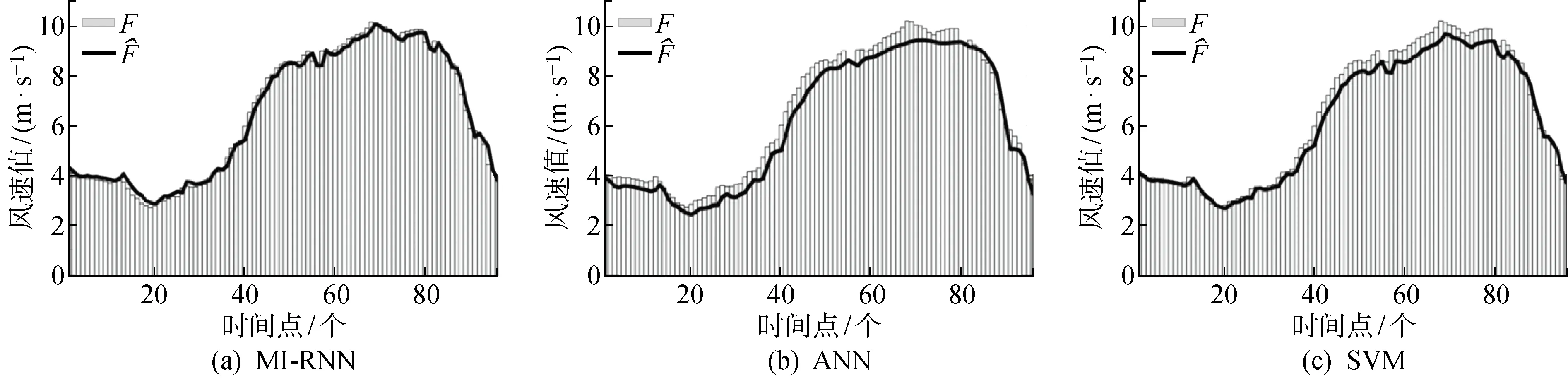
图6 观测间隔为15 min的风速预测结果

图7中，MI-RNN模型的RMSE和MAE值均最小，R2值最大，说明MI-RNN模型的预测精度最高.3个模型在3个评估指标下的详细统计结果如图表2所示.其中，MI-RNN模型的R2值最大，且其RMSE和MAE值比ANN模型的均降低了50%以上，比SVM模型的分别降低了约21%和41%.进一步表明MI-RNN模型在提高预测精度方面的优势明显.

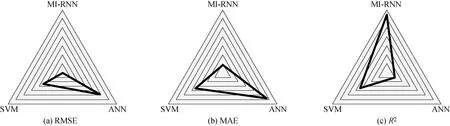
图7 模型在不同指标下的评估结果

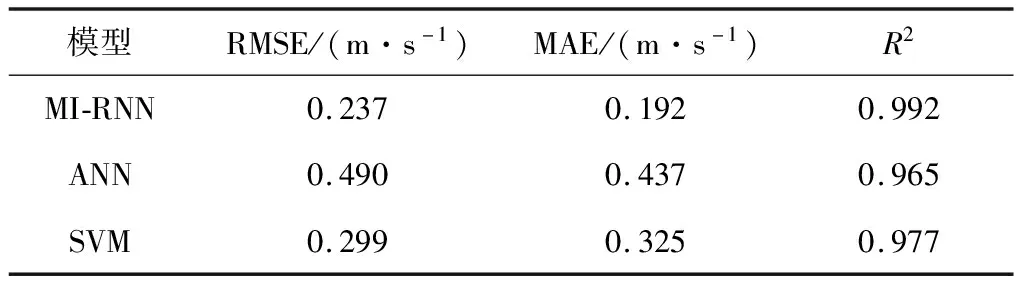
表2 模型在不同指标下的统计结果

图8中，直线由预测值等于观测值的数据点组成，MI-RNN的预测结果均匀地分布在直线附近，数据点距离直线较近，表明MI-RNN模型的预测结果更接近于观测值，且不受风速大小影响.而ANN模型的预测结果距离直线较远，且在直线下方的数据点较多，说明ANN模型的预测误差较大，且预测结果更容易低于观测值.在风速较大时，SVM模型的数据点更多地集中在直线下方，说明其预测结果在风速较大时更容易低于观测值.

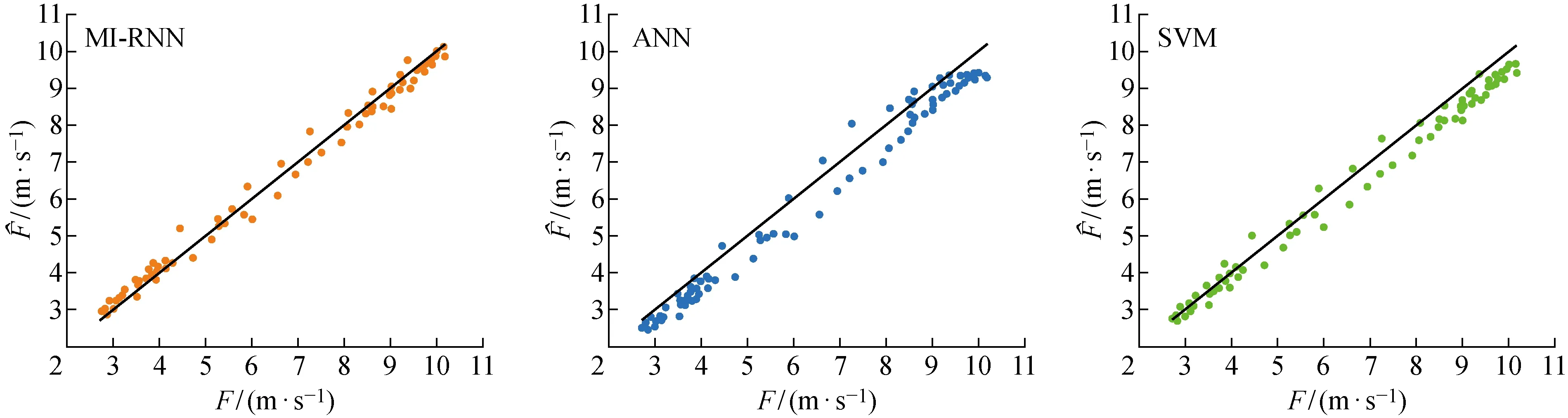
图8 风速预测结果分布图

综上所述，相比于ANN和SVM模型，MI-RNN模型能够显著提高风速预测精度，且预测稳定性良好，可以更精准地预测未来风速.

3.2 算例2

探讨不同预报提前量条件下MI-RNN模型的预测效果以及风向预测性能.

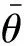
表3 观测间隔为5 min的风速数据集的统计信息

3.2.2结果与讨论 为加强模型预测结果的可视化，选择测试集中前96个时间点的数据进行结果展示.对3个模型在不同预报提前量下的预测误差结果作图，如图9所示.当预测间隔为5 min时，MI-RNN模型的风速预测结果如图10所示，其矢量图如图11所示.

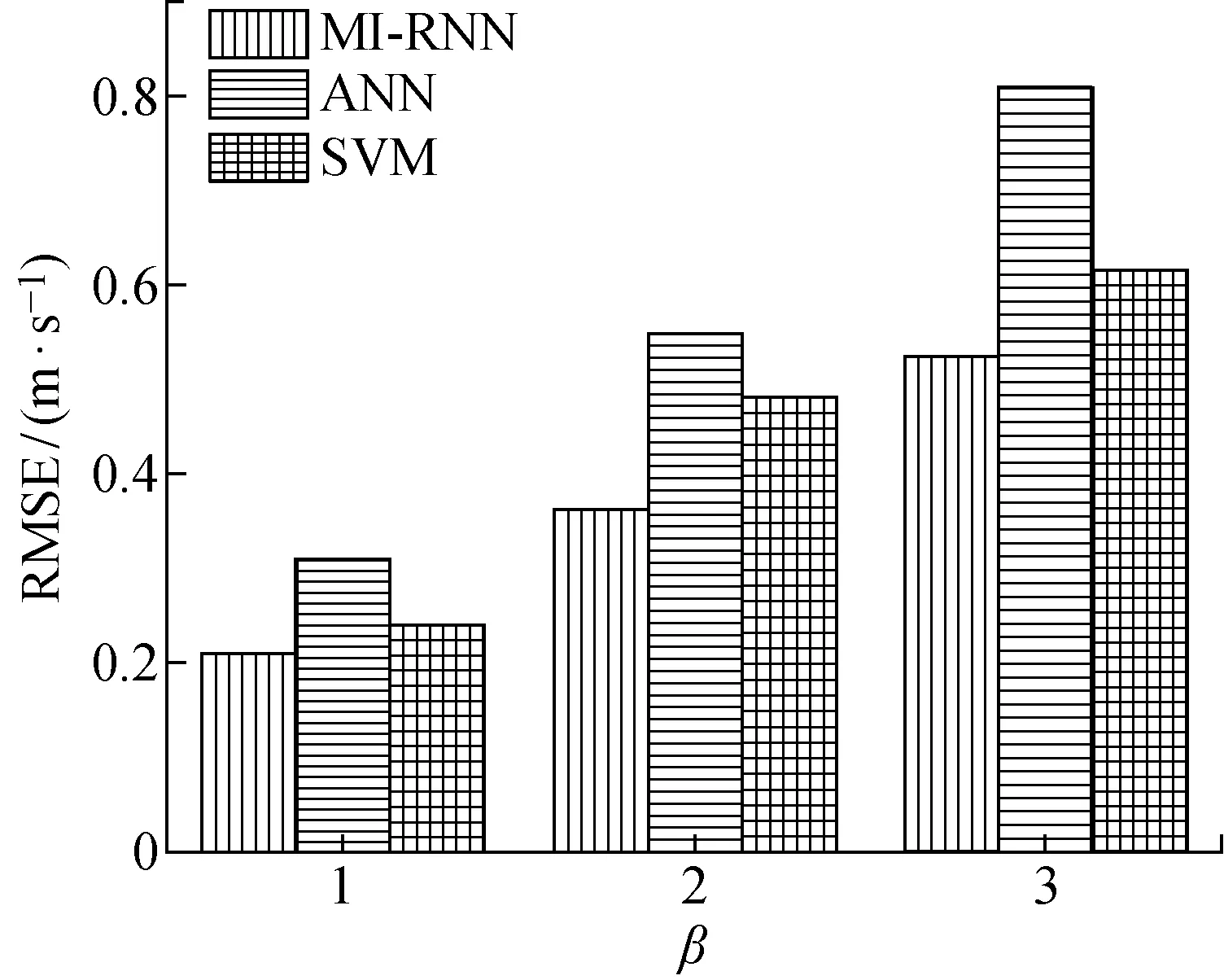
图9 模型在不同预报提前量下的RMSE对比

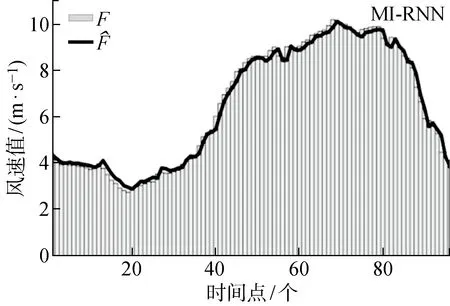
图10 预测间隔为5 min的风速预测结果

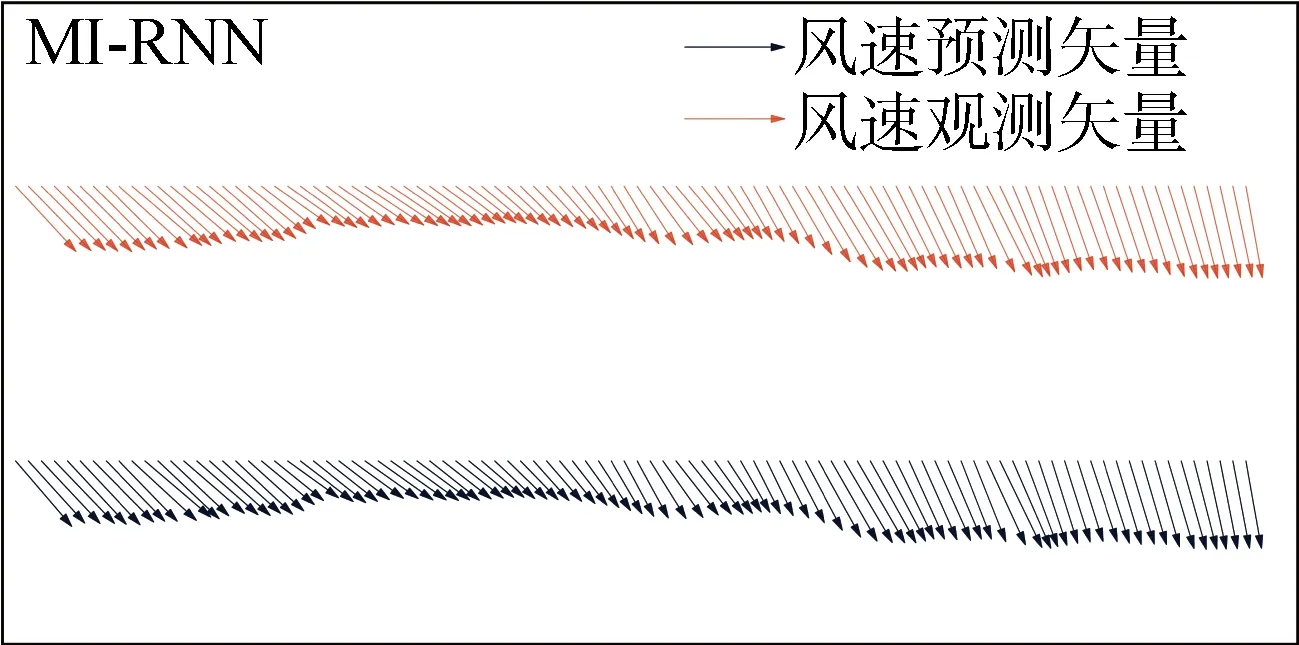
图11 风速预测结果矢量图

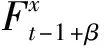
图10中，MI-RNN模型的风速预测值与观测值相差很小，在不同风速变化区间表现稳定，预测精准；在图11中，MI-RNN模型的预测风向与观测风向值之间的误差也较小.说明MI-RNN模型不仅能够降低风速预测误差，还能够精确地预测未来风向信息.

4 结论

风速的波动性和随机性给风电并网造成安全隐患，影响风能利用质量，高精度的风速预测是解决该问题的方法之一.本文提出MI-RNN模型，并将MI-RNN模型应用于美国加利福尼亚州某风电场真实数据集，验证模型的预测精度，同时使用RMSE、MAE和R2等指标评估模型的点预测结果，主要结论如下：

(1)ANN和SVM模型对风速在不同变化区间的预测精度不稳定；在风速较大时，易出现预测值小于观测值的情况.

(2)相对于ANN和SVM模型，MI-RNN模型在不同预报提前量下的预测结果误差均最小，风速预测精度更高，且风速越大其精度提升越显著；同时能够准确预测未来风向.

(3)MI-RNN模型能够应用于风电场短期(未来1 h内)风速预测，提高风电场输出功率预测精度，降低大规模风电并网安全隐患.

文中研究了单个空间点的风速预测，下一步将研究深度学习方法在含空间维度的风电场风速预测中的应用.