基于泥浆平衡地压的桩孔稳定性分析及支护建议
熊国军,王建华,陈锦剑
(上海交通大学 船舶海洋与建筑工程学院, 上海 200240)
桩基础是最为普遍的一种深基础形式,由桩孔施工引起的孔周应力状态发生改变,直接影响着孔壁的变形与稳定.文献[1]应用弹性理论和塑性力学中的屈服准则导出钻孔灌注桩孔壁的稳定条件.文献[2]采用自重竖向应力、侧压系数表达侧压力、平面轴对称弹性解等基本假设与力学概念分析了孔周围应力,结合屈服准则研究了塌孔机理,并建立了孔壁的稳定条件.文献[3]根据楔体在自重与两侧摩阻力作用下的平衡推导了自稳的临界深度.文献[4]基于孔壁内、外侧静力关系与圆孔稳定原理建立了钻孔孔壁稳定条件,基于朗肯土压力推得黏性土中稳定自立的最大深度与孔壁稳定的安全系数,基于平面滑块的静力平衡推导砂土中桩孔的安全系数.文献[5-6]基于数值模拟与实际工程分析了孔径、孔深、海水、地层土体状况、钢护筒长度、泥浆容重、成孔时间对桩孔变形与稳定的影响.文献[7]采用经典土压力理论建立了某大直径污水井孔壁失稳分析模型,分析了各因素对稳定性的影响.文献[8-9]基于Berezantzev的轴对称主动土压力公式推导了无支护挖孔临界深度的隐式公式和一种简化公式.文献[10]将饱和软土中的桩孔稳定问题视为平面圆孔的卸荷收缩问题,基于修正剑桥模型采用应力空间变换法推导了孔壁临塑支护荷载与孔壁收缩的解析表达,给出了护壁泥浆最小重度的确定方法.
总体来说,桩孔稳定性研究可分为4类:① 将桩孔稳定问题视为平面轴对称极限问题[1-3],应用弹性力学和塑性力学中的屈服准则,推导孔壁稳定条件,并利用极限分析原理对无支护极限孔深、泥浆容重等问题进行计算;② 将桩孔稳定问题视为竖面上的平面极限问题[4,7],运用朗肯土压力、库伦土压力与泥浆压力相平衡的原理建立桩孔稳定的力学模型,推导无支护极限孔深、稳定系数与泥浆容重;③ 将桩孔稳定问题视为空间轴对称极限问题[8-9],运用Berezantzev的轴对称主动土压力理论计算无支护极限孔深;④ 利用有限元软件[5-6]对影响孔壁稳定的各因素进行模拟,并提出治理措施.前三者属于理论研究,第①、②类研究均将桩孔稳定视为平面极限问题,局限性明显;第③类研究虽采用空间轴对称极限理论,但Berezantzev公式[11]是基于完全塑性假定建立的,其不合理性已在文献[10]中被深入探讨,由此推导出的无支护极限深度也存疑,且现有的第③类研究也不全面,没有给出护壁泥浆合理的容重确定方法.
针对第③类研究的不足,本文基于严格的轴对称主动土压力理论[12-13]与泥浆平衡地压原理,重新建立了分析桩孔在稳定时的力学模型,根据土压力与泥浆压力之间的关系分析了无支护成孔、泥浆护壁成孔与硬支护成孔的适用条件与范围,给出泥浆重度的确定方法.
1 桩孔稳定性分析模型
根据文献[4, 7, 14],桩孔失稳很大程度上是由桩孔开挖前后孔壁两侧压力改变所导致的.假设桩孔壁处存在一层假想薄膜,根据侧压平衡原理建立如图1所示的桩孔稳定性分析模型.其中:po、pa分别为静止土压力和主动极限土压力;γsw为泥浆重度;q为地表荷载;z为竖向;r为径向;A为桩孔与地面的交点;B为破坏面与地面的交点;E为破外面与桩孔的交点.
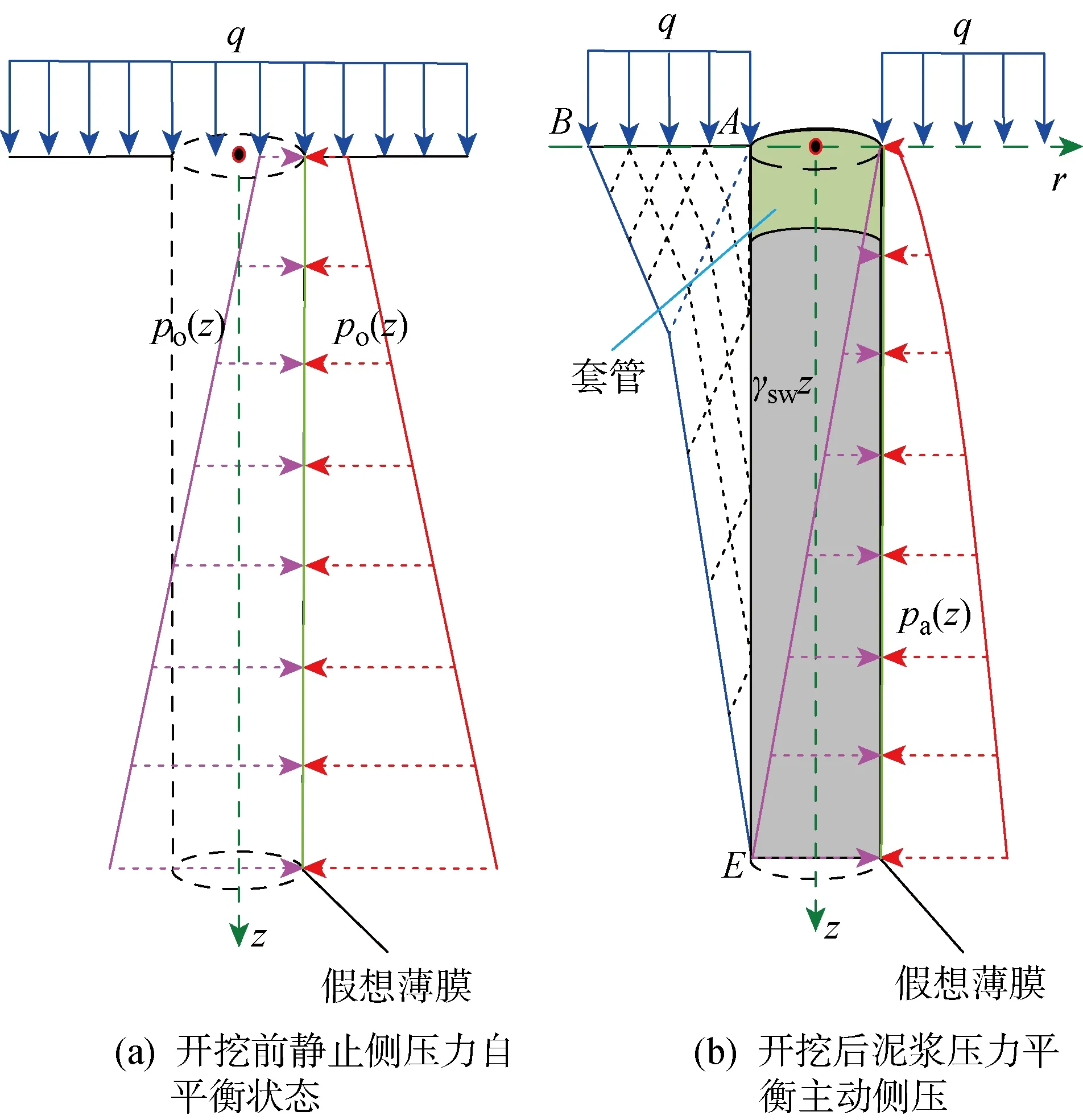
图1 桩孔开挖前后侧压状态示意图
开挖前的静止侧压力自平衡状态如图1(a)所示.假想薄膜在两侧静止土压力po(z)=Ko(γz+q)下处于自平衡状态,Ko为静止土压力系数,γ为土体重度.开挖后的泥浆压力平衡主动侧压如图1(b)所示.孔内土体被泥浆代替,孔壁向内侧移动达到主动极限状态,薄膜外侧受有主动土压力pa(z),内侧受有泥浆压力psw(z)=-γswz,在二者共同作用下达到新的状态,作用在薄膜上的pa(z)与净合力pj(z)分别为
pa(z)=γRAfaγ+qkaq+ckac
(1)
pj(z)=pa(z)-γswz
(2)
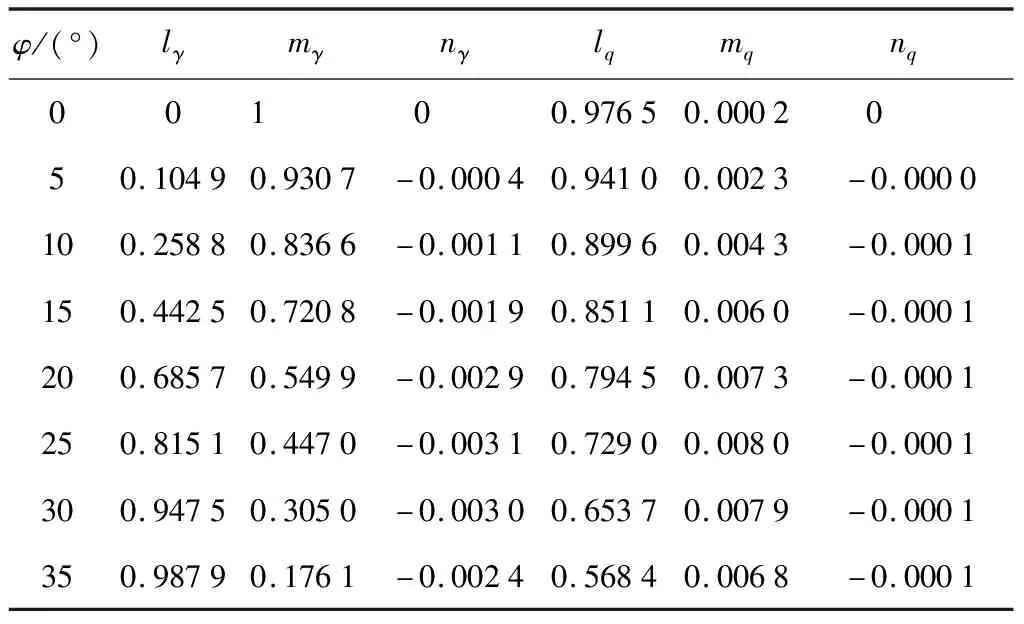
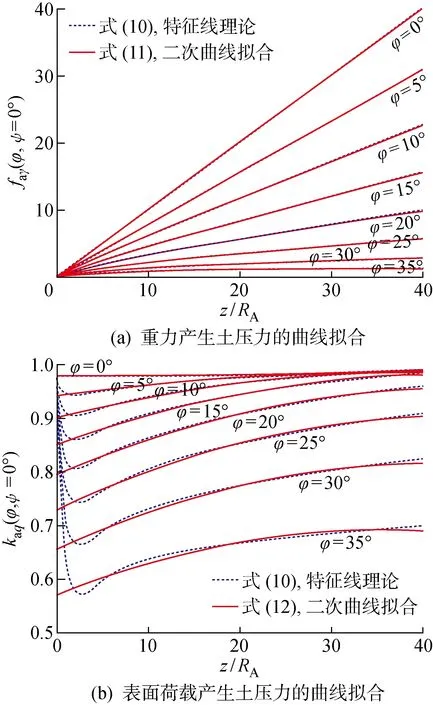
式中:RA为桩孔半径;kaq、kac分别为表面荷载与黏聚力的土压力系数;faγ为由重力产生的主动土压力的无量纲函数;c为土体黏聚力.泥浆侧压力-γswz与黏聚力产生的侧压力ckac均为负值,二者是维持桩孔稳定的要素;土体自重产生的侧压力γRAfaγ与表面荷载产生的侧压力qkaq均为正值,二者是导致桩孔失稳的因素.当净合力pj(z1 为确定圆形开挖过程中的主动极限土压力pa(z),文献[15-17]已经深入阐述了现有轴对称极限平衡理论中存在的局限性,并基于轴对称问题的静力平衡条件、相容性条件与Drucker-Prager屈服准则建立了理论上较为严格的轴对称特征线理论及轴对称主动土压力的计算方法[12-13]: (3) (4) (5) (6) (7) (8) (9) 式中:正号、负号分别表示沿着β线、α线的特征关系;R、Φ分别为子午面上的最大切应力和较大的主应力与径向坐标方向的夹角;S为特征线弧长;ΩRθ、ξR、ξθ、ErR、EzR、Erθ、Ezθ为系数,其表达形式及其推导过程详见文献[12].根据特征线表达式(7)与应力方程表达式(8)和(9)建立差分迭代式,结合边界条件便可逐步计算出3个桩孔周围特征量R、σθ、Φ的分布场,孔壁上各点的特征量用Rs、σθs、Φs表示,则作用在假想薄膜外侧的主动土压力为 (10) 文献[12]已经证明了土压力系数kac、kaq之间的关系kac=(kaq-1)tanφ,φ为土体的摩擦角,并采用实验数据[18]与数值结果[19]验证了该理论方法,即式(10)的合理性,本文对此不再赘述.为了便于分析桩孔的稳定,采用二次曲线拟合该理论的计算结果,拟合函数如下: (11) (12) 表1 6个拟合系数的取值 重力与表面荷载产生土压力的曲线拟合效果如图2所示,其中:ψ为土体的剪胀角.由图2(a)可知,式(11)对由重度产生的土压力拟合地非常好.由图2(b)可知,式(12)对由表面荷载产生的土压力在深度大于2.5倍孔径范围内也能近似地拟合.由于桩孔的整体稳定不会发生在浅部,且坑口通常也常采用钢套管以防局部破环,所以可以认为式(12)的拟合对此问题仍然适用. 图2 二次函数对土压力理论计算结果的拟合效果 根据轴对称主动土压力的计算理论,表面荷载产生正的土压力是导致桩孔失稳的因素,因此,在桩孔施工中通常不会在坑口大量堆载,本文研究也不再考虑表面荷载的影响.桩孔的设计开挖深度用H表示, 将式(12)、(13)和由文献[13]已经证明的数学关系kac=(kaq-1)tanφ代入式(1)和(2),所获得的开挖深度范围内(0 (13) (14) 由于泥浆太稠,流动性差,不便于施工,《建筑桩基技术规范》[14]第6.3条规定了泥浆重度的上限值为12.5 kN/m3,即护壁泥浆须满足上限要求 γsw≤γsw_max (15) 图3 主动土压力在开挖深度范围为负的两个实例 (16) 根据式(16),可得: (17) (18) (1)当式(18)的一次项系数小于0,即 (19) 当0≤z<+∞时,式(18)恒成立,这意味着泥浆压力可以在无限深度内平衡地压.当0≤z 图4 净压力无限深度范围为负的两个实例 (20) (21) 图5 孔口净压力为负而逐渐过渡为正的两个实例 表3 不同摩擦角与相对黏聚力下的 表4 不同摩擦角与相对黏聚力下的 (22) [(γsw/Ka-mγγ-mqccotφ)2+ 4(nγγRA+nqccotφ)× (ccotφ/Ka-lγγRA-lqccotφ)]1/2/ (2nγγRA+nqccotφ) (23) 由表4可知,当φ=5°且c/(γRA)≥4时,泥浆护壁开挖的最大无量纲深度均大于100.这表明除了淤泥、淤泥质土外,泥浆护壁挖孔方式几乎是普遍适用的. 除了2.1节与2.2节的情况之外,当H的无量纲值既不满足表2的无支护开挖深度,也不满足表5的泥浆护壁开挖的最大开挖深度时,表明土体性质太差,需要考虑采用“成孔与灌注同时进行”的施工方式,或者是全程采用“硬支护成孔”的施工作业方式. 本文通过力学建模对桩孔开挖过程中孔壁的稳定性进行了研究,并根据场地土体性质与桩的几何尺寸研究了无支护开挖、泥浆护壁成孔、硬支护成孔3种施工方式的适用范围与使用条件,具体获得如下结论. (1)基于泥浆压力平衡地压原理和轴对称主动土压力的计算理论,建立了桩孔开挖过程中孔壁稳定性分析模型.开挖后,孔壁在内部泥浆压力、自重产生的土压力下达到新的状态,二者的净合力为负,表明泥浆压力与土体黏聚力所能提供的抗失稳侧压大于自重产生的失稳侧压,孔段稳定;二者的净压力为正则意味着抗失稳侧压小于失稳侧压,孔段不稳定;二者的净合力为0,则孔壁恰好处于临界状态. (2)土体的黏聚力、摩擦角和泥浆重度是维持桩孔稳定的基本要素.当开挖深度不大于该场地的临界深度,应采用无支护开挖以节省成本;当场地土的摩擦角大于35°且相对黏聚力大于1,摩擦角等于30°且相对黏聚力大于5时,摩擦角等于25°且相对黏聚力大于10时,无支护开挖的临界深度均大于100倍的桩径.在实际工程中可以认为无支护开挖是普遍适用的. (3)当桩孔设计深度大于无支护开挖的临界深度时,采用泥浆护壁方法辅助成孔,且泥浆重度不得低于下限临界重度;当摩擦角不小于25°、摩擦角等于20°且相对黏聚力大于10时,可任意选择泥浆重度;其他情况均需要根据摩擦角与相对黏聚力选择泥浆重度. (4)当计算得到的护壁泥浆下限容重大于规范规定的最大重度12.5 kN/m3,且桩孔设计深度不大于泥浆护壁成孔的最大支护深度时,护壁泥浆应采用规范规定的最大重度12.5 kN/m3;当桩孔设计深度大于泥浆护壁成孔的最大支护深度时,则需要采用套管等硬支护措施.

2 桩孔稳定与支护方案讨论
2.1 无支护挖孔条件
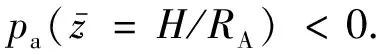
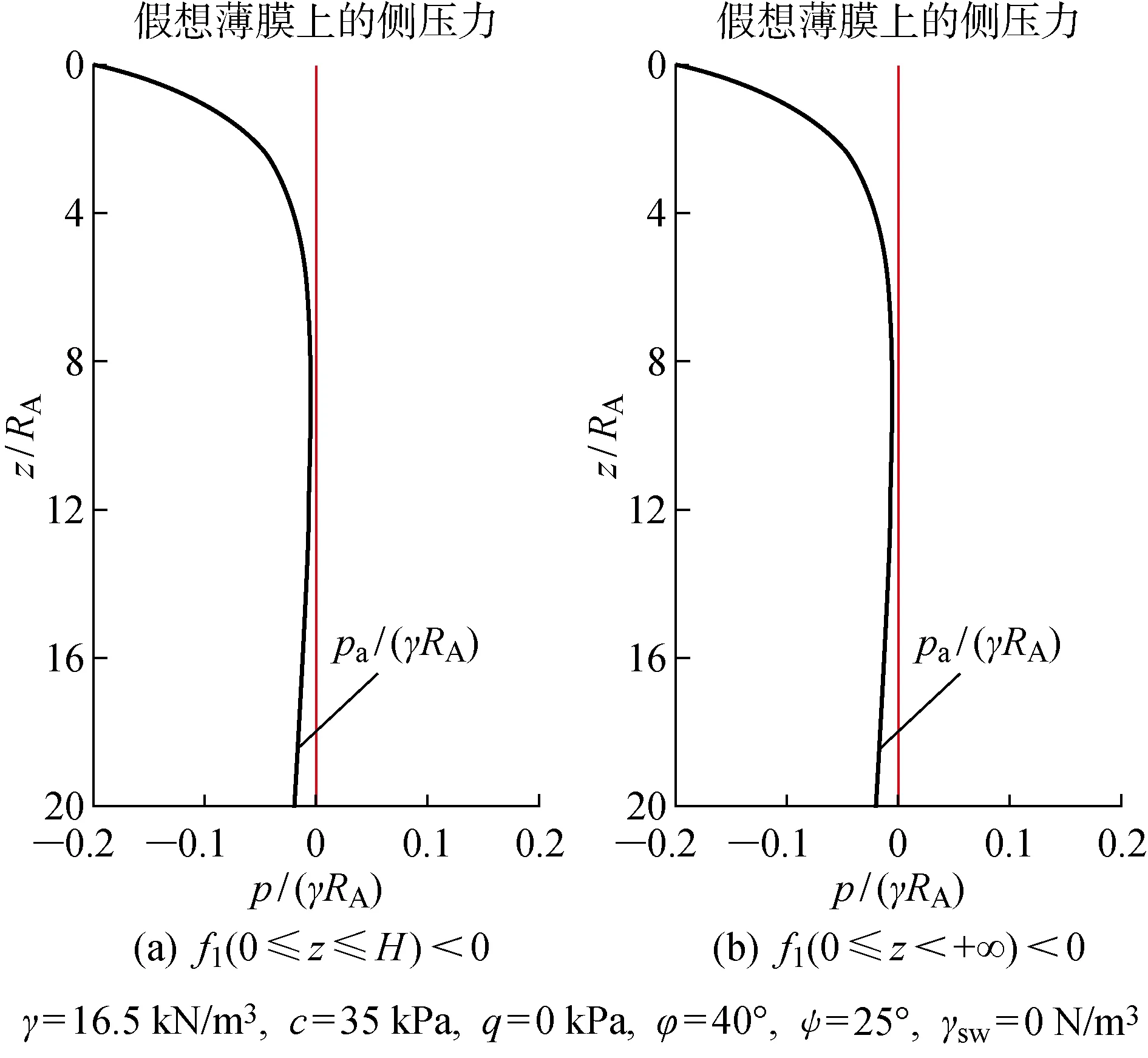
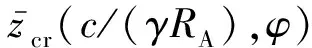
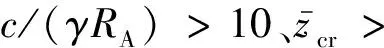
2.2 泥浆护壁成孔
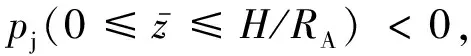



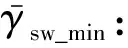
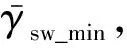

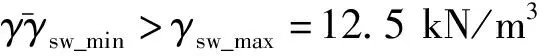



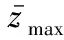

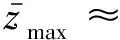

2.3 全程硬支护成孔与灌注
4 结论

