“圆的组合图形”的教学实践与思考

【摘 要】文章通过对“圆的组合图形”的教学实践与思考，将教材的例题和习题进行了有效整合，实现对教材的有效开发。在教学过程中，利用变式教学，渗透化零为整、等积代换等数学思想，帮助学生构建知识网络，提升学生的几何思维水平。

【关键词】教材开发;有效整合;几何思维水平

【作者简介】田志锋，高级教师，淮北市学科带头人，教育部“跨世纪园丁工程”国家级骨干教师培训学员，安徽省小學数学教学专业委员会理事、教科研指导委员会委员，主要从事小学数学教育教学研究工作。

【基金项目】安徽省教育科学研究项目2019年度立项课题“构建小学数学教师群体成长的教研共同体的实践研究”（JK19086）

在小学数学课堂教学中，教师要有意识地提高学生的问题意识，让学生学会思考，进行批判性的质疑，实现对数学活动的深度参与和对数学知识的深度理解[1]。也就是说，教师要顺着学生的问题引领学生思考，促进学生创新思维的发展。同时，学生的质疑能给教师带来新的教学思路，给课堂教学提供更广阔的空间，促进教师对教学素材进行有效整合，使课堂焕发生机，使学生学习充满活力。本文以“圆的组合图形”为例，分析促进学生思维发展的教学实践与思考。

一、教前慎思

（一）学生的困惑

笔者研究“圆的组合图形”这个课题，缘于在教学人教版数学六年级上册第69页“外方内圆” “外圆内方”的例题后，有学生提出疑问：“为什么不讨论它们的周长，周长该怎样求？”为此，笔者对学生进行了一次教前测试：如图1所示，正方形的边长均为4cm，指出并计算图中阴影部分的周长。

结果显示，有不少学生没能正确指出阴影部分的周长，部分学生能正确指出并计算，但没有转化意识，不能将图形化零为整地考虑，以致计算过程过于复杂、烦琐。另外，教材中零散分布的圆的组合图形习题，只能让学生就题论题，不能让学生系统地掌握解决此类问题的思想方法，以致学生遇到类似的变式题时，或疲于应付，或无所适从，未能有效解答问题。

（二）教材开发

人教版数学五年级上册设置了“组合图形的面积”一节内容，但限于学生的知识储备量，只讨论直线型的组合图形，仅要求学生会认识简单的图形并求出它们的面积。人教版数学六年级上册“圆”单元中，穿插设置了很多有关圆的组合图形的例题和习题，不仅涉及求面积，而且要求求出周长，如求出拱形门、太极图、半圆环、操场跑道的周长等。

笔者将零散分布的有关圆的组合图形的例题和习题进行了整合，通过在正方形内画最大的圆等一系列数学学习活动，引导学生经历圆的组合图形的形成过程，掌握计算圆的组合图形的周长和面积的基本思路和方法，渗透转化、分类、优化等数学思想方法，培养学生的直觉思维、求异思维、创新思维等，实现对教材的有效开发。

（三）理论践行

范希尔理论将学生的几何思维水平分为三个层次：一是直观水平，要求学生能整体地认识几何对象;二是描述水平，要求学生能按照图形的组成部分和组成部分之间的联系来分析图形;三是理论水平，要求学生能利用演绎推理证明几何关系，发展逻辑推理能力[2]。与之相一致，《义务教育数学课程标准（2011年版）》也明确提出，在数学课程中，应当注重发展学生的数感、空间观念、几何直观、推理能力等[3]。

按照范希尔的观点，学生几何思维水平的提升是经由教学，而不是随年龄增加或心理成熟自然而然提升的;不同几何思维水平之间的过渡是不平缓的，而是要经历一个“思维危机”过程[4]。如何让学生平稳渡过“思维危机”，促进思维水平的顺利提升？笔者认为，对“圆的组合图形”的研究学习是一次比较有益的理论实践，利用变式教学，能够很好地实现描述水平向理论水平的平稳过渡，而在此基础上发展起来的逻辑推理能力，能够为下一阶段的平面几何知识学习做铺垫。

二、教学实践

（一）课件展示，揭示主题

教师用课件展示一个正方形和一个圆，动态演示组合成“外方内圆”的过程，并指出本节课的课题：探究“外方内圆”这类组合图形的周长和面积。

（二）直观操作，体验本质

1.初步感知组合图形周长和面积的本质区别

教师出示问题：边长为4cm的正方形内如何画一个最大的圆？并计算出圆的周长与面积。

学生在课前准备好的正方形纸上试画并计算出具体数值，发现圆的周长和面积的数值都是12.56，但单位不同。

师：除了单位不一样，你还能从图中找出它们的不同吗？

生（用手比画）：周长是圆一周的长度，面积指圆的大小。

【设计意图】通过这个教学环节，将教材例题与习题有关“外方内圆”的知识点进行有效整合，追本溯源，还原“外方内圆”的形成过程。同时，将圆的直径设为4cm，并要求学生从图形中辨认出圆的周长和面积，以防学生仅识记单位形式上的不同，而忽略本质上的区别。

2.涂出圆与正方形之间的图形，并描出其周长

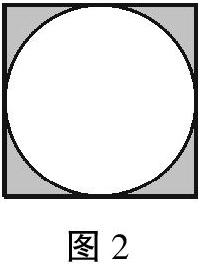
师：同学们，通过描线，你们发现涂色部分（如图2）的周长由几部分组成？

生1：由一部分组成，也就是正方形的周长。

生2：应该由两部分组成，即正方形的周长和圆的周长。

生3：不对，我觉得应该是四部分组成。

看到大家有些疑惑，教师示意生3继续回答。

生3：我认为是由4个“小角”组成，所以涂色部分的周长应该是4个“小角”的周长之和。

此时，学生出现两种意见：一种是支持生2的观点，另一种是赞同生3的看法。

师：对于图中的“小角”，我们不妨称之为曲边三角形。大家想一想，这4个曲边三角形的周长是不是等于正方形的周长和圆的周长之和？

学生表示同意。

师：因为这4个曲边三角形是连接在一起的，所以我们也可以把涂色部分的周长看作正方形的周长和圆的周长两部分组成。

【设计意图】通过涂一涂，描一描，使学生意识到涂色区域的大小就是涂色部分的面积，描线的长度就是涂色部分的周长，让学生进一步辨析组合图形周长与面积的本质区别。特别是讨论涂色部分的周长时，教师引导学生将其视作正方形的周长与圆的周长组合而成，培养学生的辨析能力，促进思维生长，同时也渗透化零为整的数学思想。

3.多组图形类比，掌握组合图形周长和面积的计算方法

（1）周长的计算方法——化零为整

教师出示下列一组图形（图3至图5），正方形的边长均为4cm，学生在答题纸上描出每个阴影部分的周长，计算并比较其大小。

师：通过前面的描线，我们知道图3的阴影部分的周长=正方形的周长+圆的周长。

师：图4的阴影部分的周长是多少？图5呢？

师：同学们，请想一想，哪一种方法计算更简便呢？

大多数学生都觉得生2的做法比较简便。

【设计意图】教师引导学生观察图形的特点，运用化零为整思想，将其转化为求圆的周长，这样的教学思路不仅体现整体性思维，而且体现化归的数学思想方法，让学生感受数学的奇妙，体会优化的解题策略。

（2）面积的计算方法——割补法（平移或旋转）

4.拓展延伸，探究圆与长方形组合图形的面积

教师引导学生思考：将正方形变成长为13cm，宽为4cm的长方形，如何画出最大的圆？最多能画几个？学生之间互相讨论交流，在课前准备好的长方形内试画。最后，学生汇报操作结果：最多能画3个最大的圆（如图6）。教师通过课件演示画圆的方法和个数，使学生明白长方形的宽决定圆的大小，长方形的长决定圆的个数。同时，引导学生得出：余下部分的面积=长方形的面积-3个圆的面积，让学生体验圆与长方形组合图形的面积形成过程。

【设计意图】教师利用变式教学，改变条件，将正方形变为长方形，探究如何画出最大的圆，最多能画几个，余下部分的面积是多少等一系列问题，为学生提供尝试发展的阶梯。由于前期的铺垫，学生很容易将正方形内画最大圆的方法类推到长方形内，并且发现画出的圆的多少由长方形的长决定。在求余下部分的面积时，学生类比联想到正方形内涂色部分的面积，再次理解二者的本质相同之处，使问题得以顺利解决。这一教学环节的设计，让学生的思维拾级而上，既增强了学生的学习信心，又提升了学生的迁移能力。

（三）提升练习，优化解题策略

练习1 不必计算，直接比较图7、图8阴影部分的周长和面积的大小。（单位：cm）

题目虽然不用计算，但教师仍给出数据的目的是让学生认真读取图中的数学信息，读懂阴影部分都是由三段分别相等的半圆弧组合而成。繼而得出：两个图形周长相等、面积不相等，图8的阴影部分的面积更大。

【设计意图】通过练习1，让学生对图7和图8进行类比，有意识地培养学生在解决组合图形问题时养成先观察再判断的习惯，进一步提升学生的几何直观水平、描述水平和理论水平。

练习2 如图9所示，已知长方形的面积等于圆的面积，圆的半径是10cm。求：（1）阴影部分的面积;（2）阴影部分的周长。

【设计意图】通过练习2，让学生学会认真读题、读图，并懂得选择最优化的解题策略——等积代换和化零为整，练习2充分体现算法的多样化和优化，有利于学生思维品质的提升。

（四）梳理沟通，构建知识网络

在最后环节，教师引导和帮助学生回顾学习过程、梳理知识，并对知识进行内化建构（如图10）。通过这样的整合活动，使学生将所学知识内化成自己的观点和思想，懂得将图形对象和关系的研究进化到一个新的思维领域，从而获得新的思维水平。

三、教后感悟

（一）整合教材，促进知识理解

心理学的研究表明，学习材料只有组织成系统，才会被学生迅速、准确而牢固地掌握并迁移，而这个系统应该是有序的、有层次的[5]。课堂上，教师将教材中零散的例题和习题进行整合，并且把例题中只解决组合图形的阴影部分面积拓展为既研究周长问题，又研究面积问题。这样的统整更能加深学生对概念的理解，通过类比、归纳，促进学生对知识的理解。

（二）深度引导，优化解题策略

在研究正方形内如何画最大的圆时，教师引导学生动手画一画、涂一涂等活动，让学生初步感知组合图形的周长与面积的本质区别。在探究圆与正方形组合图形的面积与周长的求法时，教师放手让学生自己解决，尽管有的学生算法烦琐，但是他们经历了解决问题的过程，锻炼了解决问题的能力，并且部分学生由此想到化零为整的数学思想。同时，教师引导学生运用旋转、平移等方法，渗透了图形运动、类比转化、优化算法的数学思想，促进了学生的思维发展，优化了解题策略。

在教学拓展延伸阶段，将正方形变为长方形，拓展了学生的学习空间，培养了学生思维的灵活性。

（三）变式练习，提升思维水平

在练习1中，设计成两个图形的组成元素相同，组成形式不同，而且要求不计算直接比较大小，培养学生的直观水平、描述水平。在练习2中，教师要求学生运用等积代换和化零为整的思想方法，让学生学会优化解题策略，发展学生的逻辑推理能力。变式教学，让问题实现了有机串联，有利于加深学生对问题本质的理解，有利于学生建构完整、合理的知识网络，同时使得思维过程具有合适的梯度，过渡平缓，最终促进学生思维水平的顺利提升。

数学的本质在于思考的充分自由[6]。本节课借助圆、正方形、长方形这三个最基本的图形，巧妙组合，以点串线，让学生经历了知识的发生和发展过程。在观察、操作、独立思考中，学生掌握了计算圆的组合图形周长和面积的基本方法，在观察、比较、交流讨论中，学生能够灵活选择解决方案，优化解题策略，拓展了几何思维空间。因此，在数学教学中，教师应教会学生如何思考，提升学生的几何思维水平。

参考文献：

[1]沈君.基于数学理解的游戏教学探析：以“长方形和正方形”一课为例[J].中小学课堂教学研究，2021（2）：34-36.

[2]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[3]中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2012.

[4]鲍建生，黄荣金，易凌峰，等.变式教学研究[J].数学教学，2003（1）：11-12.

[5]陈永明名师工作室.数学习题教学研究[M].上海：上海教育出版社，2010.

[6]米山国藏.数学的精神思想与方法[M].毛正中，吴素华，译.成都：四川教育出版社，1986.

（责任编辑：罗小荧）