基于车轮磨耗和舒适度的CRH3型动车组型面优化研究

祁亚运，戴焕云，干 锋，魏 来，桑虎唐

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.西南交通大学 牵引动力国家重点实验室，成都 610031）

CRH3型动车组是我国高速客运动车组的主营列车，然而在运营后随着运营里程增加和列车持续高速运行，车轮磨耗问题成为运营过程中的主要问题，典型的车轮磨耗如图1所示，磨耗主要集中在踏面区域和轮缘根部区域。随着磨耗增大，轮轨接触关系进一步恶化。而车轮磨耗使车轮镟修里程缩短，高速动车组运营能耗增大，降低了高速列车运营的经济性[1-3]。

图1 高速动车组车轮磨耗Fig.1 Wheel wear of high speed EMUs

轮轨接触关系对于轮轨动力学行为具有重要影响，主要包括车辆运行稳定性、旅客舒适度、安全性和车轮磨耗等[4-6]。因此在踏面设计时，需要综合考虑稳定性、安全性、舒适性和经济性等相关因素。随着我国高速铁路运营里程的不断增加以及高速列车运行的愈发密集，轮轨磨耗日益突出，造成动车组运行性能下降，轮轨维护成本居高不下。因此，在实际运营中出现问题时，需要对踏面进行修正设计。传统的踏面设计都是根据工程师的经验去局部调整廓形，近年来，由于多体动力学的发展，形成了以多体动力学为辅助的车轮踏面设计思路[7]。主要包括了型面生成，多体动力学计算和型面优化算法三部分组成。

型面生成是型面优化设计的核心，有很多学者提出了不同的车轮廓形生成方法。Shevtsov等[8]首先提出了以滚动半径差（rolling radii difference，RRD）为目标产生新的轮廓，优化目标是使目标RRD与实际RRD之间的差异最小，但是这一方法的目标RRD曲线的生成需要依靠丰富的经验。Cui等[9]采用了以减小轮轨法向间隙为目标，通过移动点的垂向坐标的型面生成方法。Choi等[10]采用分段三次Hermite插值多项式的方法来生成新的轮廓。Lin等[11]采用三次样条曲线的方法对生成新的地铁车轮型面，但其改变了轮缘厚度。Shen等[12]提出了在不考虑侧滚角的情况下，采用实测钢轨的接触角曲线来反求车轮踏面廓形并将其应用于独立车轮型面。Polach等[13]为了提高踏面的共形接触，减少集中磨耗，提出了一种以等效锥度为目标踏面设计方法。干锋等[14]采用轮径差为目标的反向设计方法，并以LMA和S1002为例进行验证。Spangenberg等[15]将踏面分为多个区域，优化其中的一两个区域，然后采用平滑方法平滑整个型面。Ye等[16]采用将型面垂向伸缩的方法，有效地改变了踏面等效锥度，但轮缘高度也发生变化。以上踏面生成方法大多是需要移动点、曲线拟合以及后期平滑，这都需要大量的计算，且一些型面生成后不符合相关标准，难以在工程中推广使用。本文采用了旋转压缩微调（rotary-scaling finetuning，RSFT）进行型面生成，可以避免复杂的几何设计。对于目前型面优化算法中也存在着反复迭代计算的缺陷，引入代理模型（Kriging surrogate model，KSM）来建立输入和输出的关系，加快型面优化的计算过程。

车轮型面生成后通常采用多体动力学软件（SIMPACK、Vampire、UM等）进行动力学计算。对于型面优化计算，常见的算法有遗传算法和粒子群算法。Persson等[17]采用遗传算法进行踏面优化，最后得到P8车轮型面有效地减小磨耗。Novales等[18]也使用遗传算法进行优化踏面，通过相关系数将三个优化目标转化为一个目标，转化成了单目标优化问题，优化后的车轮型面在西班牙的有轨电车上装车试验并减缓了车轮磨耗。Lin等采用粒子群优化（particle swarm optimization，PSO）算法进行型面优化设计，最终，获得了具有薄轮缘的LM踏面廓形，以增强曲线通过性能和减小车轮磨耗。Cui等引入了加权函数以将多目标优化问题转化为单目标优化问题，并采用PSO算法进行车轮型面优化。

本文首先采用RSFT法生成车轮型面[19-20]，然后建立高速动车组动力学模型，并进行动力学仿真，计算出相应的优化目标和约束条件，采用KSM-PSO算法进行优化设计。最后对优化后车轮型面的动力学特性进行验证。

1 车轮型面生成算法

目前的车轮型面设计方法已经详细论述，但设计型面过于复杂不能快速生成踏面廓形。本文采用了旋转压缩微调法对高速动车组车轮型面进行优化，引入两个参数（α1和α2）进行对S1002CN型面进行调整，主要包括了旋转、压缩、回旋、经验公式修正和横向伸缩5个步骤，现给出RSFT法的具体计算过程如下所示:

在该算法中，原始车轮型面S1002CN写为（y，z），T1和T2旋转矩阵，θ=arctan（zmax/yθ）是旋转角，zmax和yθ分别是A点的垂坐标和横坐标。首先采用旋转矩阵T1将踏面旋转为θ，得到新的曲线（y1，z1）。然后引入压缩系数α1，z2=α1z1，对原踏面的垂向坐标进行压缩，得到新的曲线（y2，z2），引入这个参数时改变等效锥度、接触角等参数，参照EN 15313标准[21]，则其取值为0.95≤α1≤1.05。随后将得到的新曲线回旋至原始坐标系，乘以回旋矩阵T2，得到曲线（y3，z3）。 在回旋后，可以发现曲线外端区域（远离轮缘的区域）发生了较大变化，而这一区域直接影响着车辆运行的稳定性和对中性能。因此，引入修正公式E x，对该区域进行局部修正，修正后使车辆临界速度能够得到保证，得到曲线（y4，z4）。最后，引入参数α2对横坐标进行伸缩，但需要注意轮缘厚度和轮缘角的大小。参照标准，将α2的参数变化范围设为0.98≤α2≤1.02。 将 α1取值为0.92，α2取值为1.02，生成的新的廓形和S1002CN廓形，如图2所示。

图2 采用RSFT方法进行车轮型面生成（α1=0.92，α2=1.02）Fig.2 Wheel profile generated by RSFT method（α1=0.92，α2=1.02）

2 CRH3高速动车组动力学模型建立

为了获得高速列车的动力学响应，首先在动力学软件SIMPACK中建立了CRH3动车组拖车车辆模型，主要包括了4个轮对，4个轴箱，两个构架和一个车体，其中轮对、构架和车体考虑6个自由度，轴箱考虑旋转自由度。采用转臂式轴箱定位装置，悬挂系统包括了一系悬挂和二系悬挂，一系悬挂系统包括一系减振器和一系刚弹簧，二系悬挂包括了空气弹簧和抗蛇行减振器，二系横向减振器，同时考虑了横止挡和抗侧滚扭杆的作用，建立动力学模型如图3所示。车轮型面采用S1002CN，钢轨型面采用CHN60廓形，轮轨法向力采用Hertz接触算法，轮轨切向力采用FASTSIM算法。

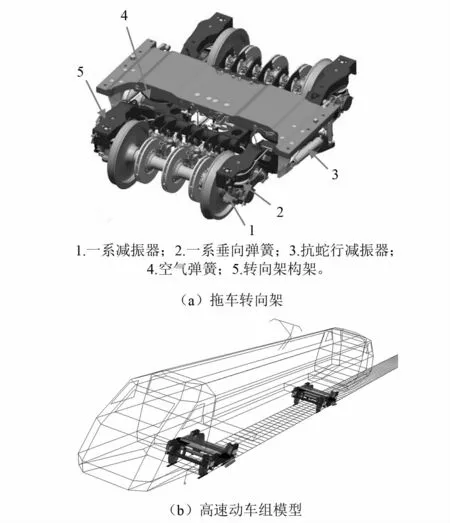
图3 CRH3车辆动力学模型Fig.3 CRH3 vehicle dynamic model

根据CRH3型动车组在武广线的实际运营情况，轨距为1 435 mm，轨底坡为1∶40。对于武广客运专线线路情况进行了调查分析，分析中轨道激励采用中武广线实测线路谱（WG谱），由于无法完全掌握该线路的所有线路分布情况，仿真分析中采用典型的运行工况，如表1所示。

表1 武广客运专线典型计算工况[22]Tab.1 Typical calculated working conditions for the Wuhan—Guangzhou passenger line

3 车轮型面优化设计

3.1 设计变量、优化目标和约束条件

设计变量:

以RSFT方法中的两个可变参数α1和α2为设计变量。

优化目标:

由于动车组车轮磨耗和旅客舒适度是需要考虑的两个重要因素，直接关系到车辆运营经济性和乘客的良好乘坐体验。本文以车轮磨耗和旅客舒适度为优化目标进行车轮型面优化。

左右车轮的踏面磨耗计算为

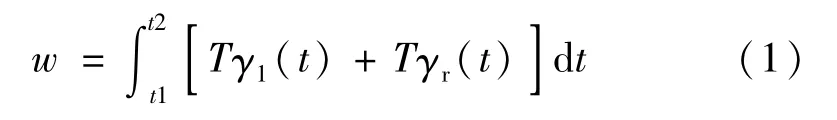
式中:Tγ1为左轮车轮磨耗；Tγr为右轮车轮磨耗；t1为积分开始时间；t2为积分结束时间。

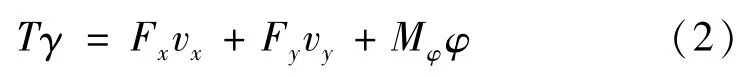
式中:Fx和vx为纵向蠕滑力和纵向蠕滑率；Fy和vy分别为横向蠕滑力和横向蠕滑率；Mφ和φ分别为自旋蠕滑力矩和自旋蠕滑率。

舒适性指标是反映旅客疲劳程度的一个指标

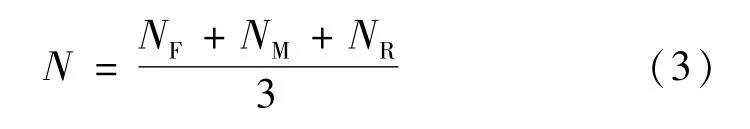
式中:NF，NM和NR分别为车体前端、中部、后部和旅客舒适度；N为整车舒适度。

式中:a为加速度均方根值；wb和wd为根据权重曲线的取值。

约束条件:

（1）轮轨横向力

横向力的限值为

式中，P0为静态的轴重。

（2）轮轨垂向力

轮轨垂向力限值要求

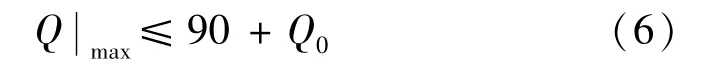
式中，Q0为一个车轮上的静载荷。

（3）脱轨系数

脱轨系数采用Nadal准则计算，其限值是0.8。

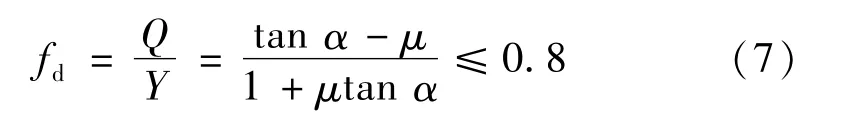
式中:α为轮缘角；μ为轮轨之间的摩擦因数。

（4）倾覆系数

轮轨间的横向力过大时容易形成倾覆，其计算方法为

式中，QiA和QiB分别为左右侧的轮轨法向力之和。

3.2 优化设计方法和流程

3.2.1 KSM模型

KSM模型是以结构分析和变异函数为基础，采用加权平均的方法对于待估点进行预测。其中权值的选择标准是使估计方差最小。采用代理模型可以有效在约束条件的作用下，建立起设计参数和优化目标之间的关系。

则写出估计值与响应值得关系式为

待拟合函数响应值和估计值关系为

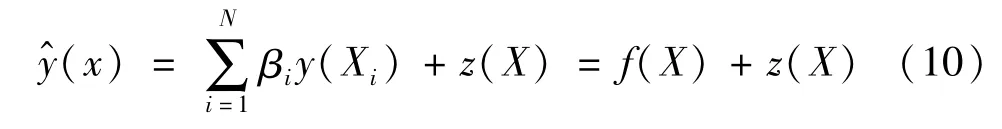
式中，z（X）为随机过程函数。

当相关函数设定后，待拟合函数

式中:Y为样本响应量矩阵；fk为列向量；Rk为样本点的相关矩阵。

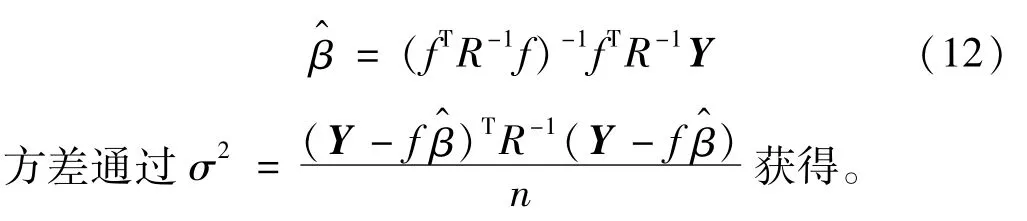
3.2.2 PSO算法

PSO算法是首先需要初始化为一群随机粒子，然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”（pbest，gbest）来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置，其计算流程如图4所示。

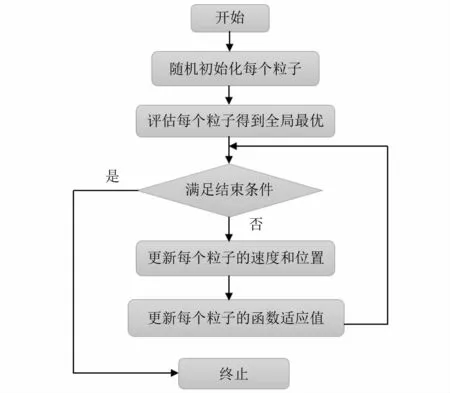
图4 PSO算法流程图Fig.4 PSO algorithm flow diagram

3.3 优化过程及优化结果

首先采用超拉丁采用对两个设计变量参数α1和α2进行选取，总共选取40个随机参数如图5所示。采用RSFT方法通过改变设计变量的值生成40个踏面，然后采用建立的动车组动力学模型得到不同踏面对应的优化目标和约束条件的值，即得到不同的优化目标（w，N）和约束条件（Y，Q，fd，η）。 然后利用KSM-PSO算法优化出最优车轮型面，具体流程图如图6所示。

图5 超拉丁采样参数选取Fig.5 Super Latin sampling parameter selection

图6 优化过程示意图Fig.6 Schematic diagram of optimization process

最后通过KSM-PSO算法进行优化，通过KSM代理模型建立设计变量和优化目标、约束条件之间的关系。再利用PSO算法求解出100个Pareto最优解，如图7所示。为了使踏面磨耗和舒适度同时最优，选择最优解（0.314，1.622）。 对应的设计变量 α1和 α2对应的值为（1.015，1.012），对应的采用RSFT方法设计出最优解型面S1002CNopt，如图8所示。新踏面和原始踏面相比轮缘高度不变，只是在轮缘根部区域和轮缘区域略有不同。接下来主要通过仿真验证优化踏面的动力学特性和磨耗性能。

图7 KSM-PSO算法优化结果Fig.7 Optimization results of KSM-PSO algorithm

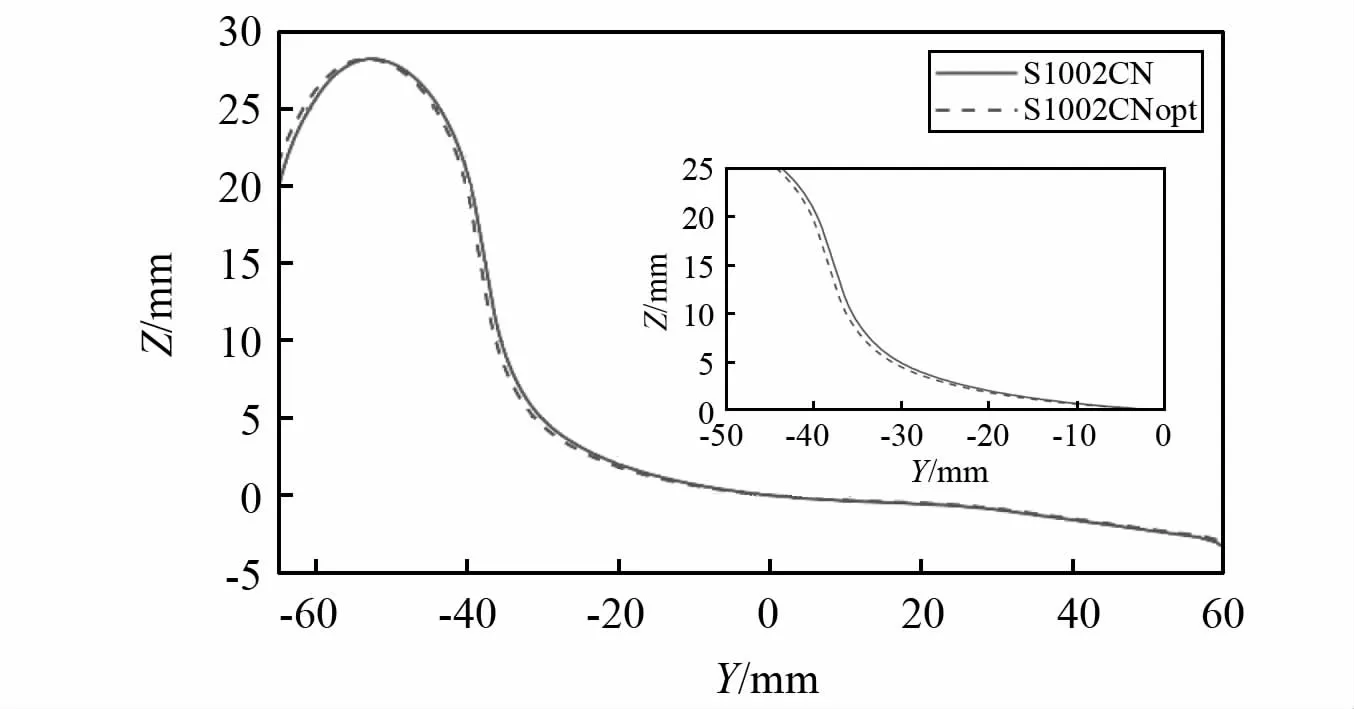
图8 优化前后廓形Fig.8 Wheel profiles before and after optimisation

4 优化后踏面的动力学特性和磨耗性能

4.1 轮轨接触特性

通过计算不同横移量下的轮轨接触点的分布可以有效看出是否发生轮轨接触点集中现象，轮轨接触点集中容易诱发踏面凹形磨耗和局部应力过大，进一步造成轮轨接触疲劳。因此，分别计算了原始S1002CN踏面和优化后的S1002CNopt踏面的轮轨接触点分布，如图9所示，可以看出，优化后踏面轮轨接触点分布更加均匀。进一步对比优化前后踏面的等效锥度，如图10所示，可以看出优化后踏面等效锥度整体减小，锥度突变点增大，原S1002CN踏面当横移量大于7.4 mm时突变，而新踏面在接触点大于8 mm时突变。当锥度较小时，两个踏面等效锥度比较接近。S1002CN踏面3 mm时等效锥度为0.175，优化后踏面等效锥度为0.15。图11中给出了优化前后踏面不同轮对横移量下的轮轨最大接触应力和接触斑面积。可以看出优化后踏面在不同横移量下的最大接触应力减小，接触斑面积进一步增大。

图9 轮轨接触点分布Fig.9 Distribution of wheel rail contact points

图10 不同横移量下的等效锥度Fig.10 Equivalent conicity of different lateral displacement

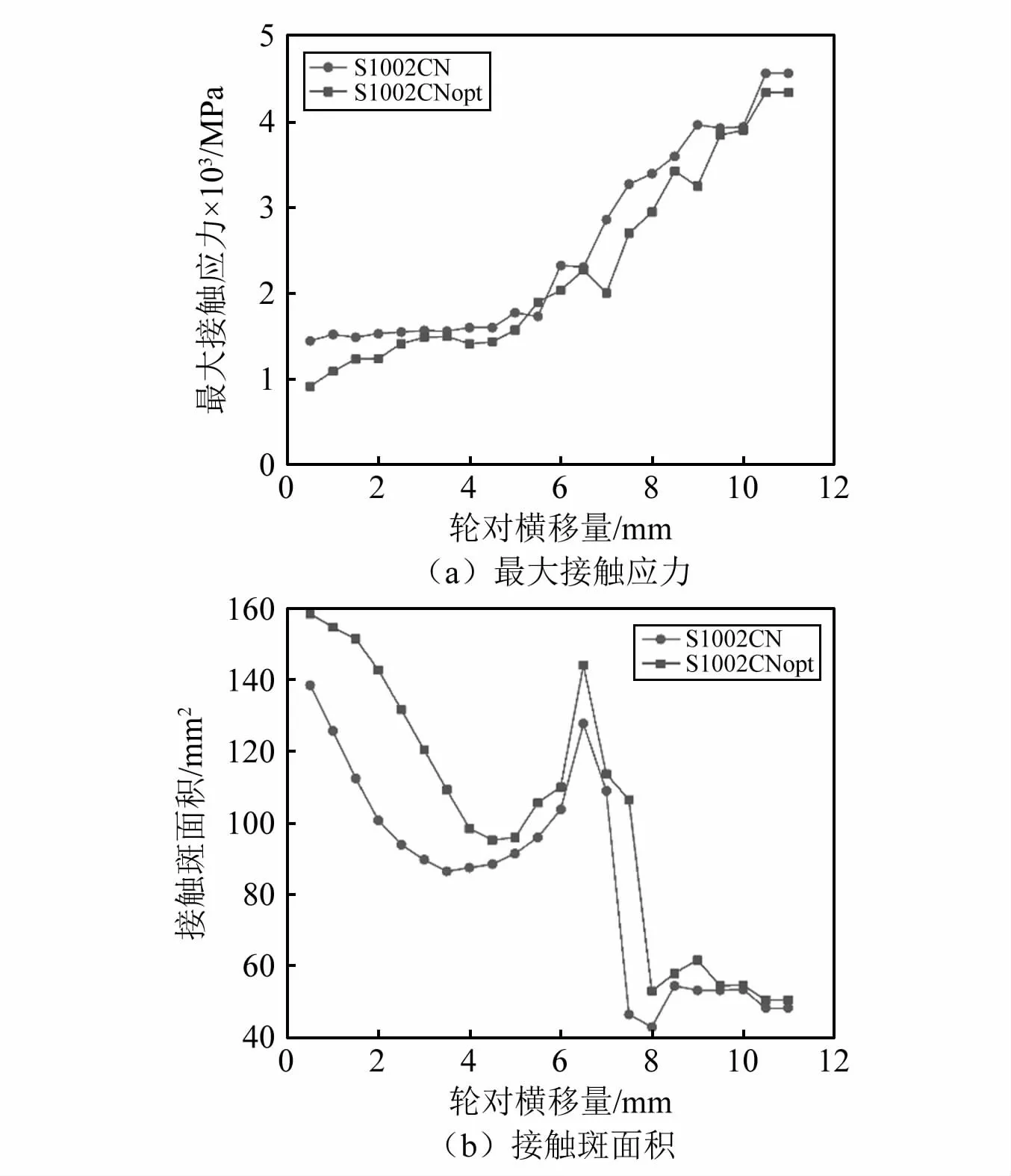
图11 最大接触应力和接触斑面积Fig.11 Maximum contact stress and contact patcharea

4.2 稳定性

稳定性是衡量车辆运行性能的首要因素，也是重要的动力学指标之一。采用降速法计算车辆的非线性临界速度。首先给整车一个较大的初始运行速度，使车辆发生横向蛇行失稳，失稳后，施加纵向作用力使车辆降速，当运动收敛后，横移量为0时的速度定义为非线性临界速度。通过以上方法计算得到如图12所示，S1002CN踏面的临界速度为525 km/h，优化后踏面S1002CNopt的临界速度为560 km/h。优化后临界速度进一步提高，我国高速动车组最高运营速度在350 km/h，满足运营要求。

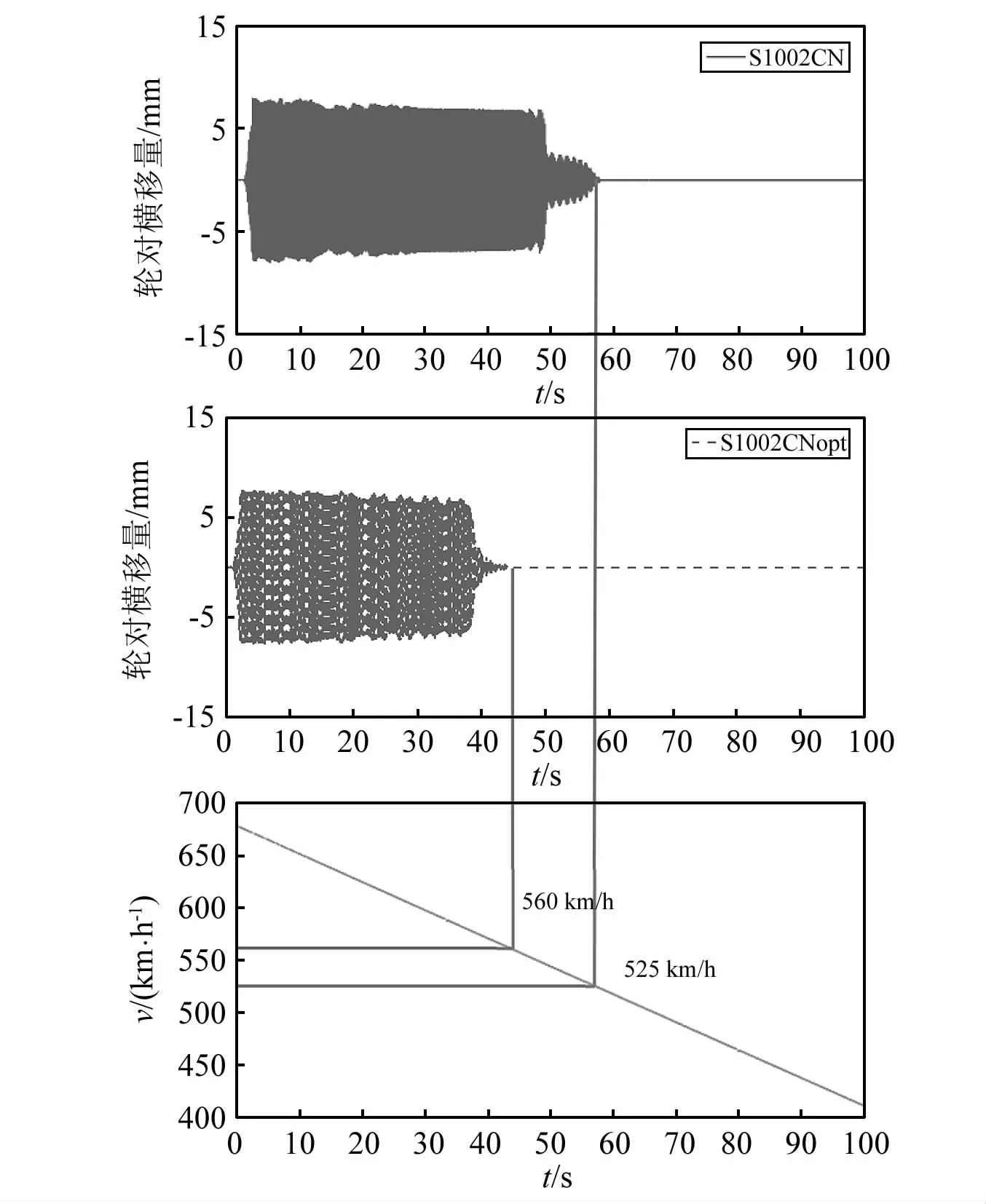
图12 非线性临界速度Fig.12 Nonlinear critical speed

4.3 运行平稳性

平稳性是车辆运行过程中重要指标，对于旅客舒适度具有重要影响。现分别计算了S1002CN和S1002CNopt车轮踏面与60钢轨廓形和60D钢轨廓形接触时的平稳性指标，其中两种轨面廓形如图13所示，60D钢轨廓形为过度打磨时的廓形。主要计算了直线工况和曲线工况。采用WG50轨道谱，曲线设置为:直线510 m，缓和曲线400 m，曲线半径5 000 m，曲线长1 500 m，超高0.175 m。

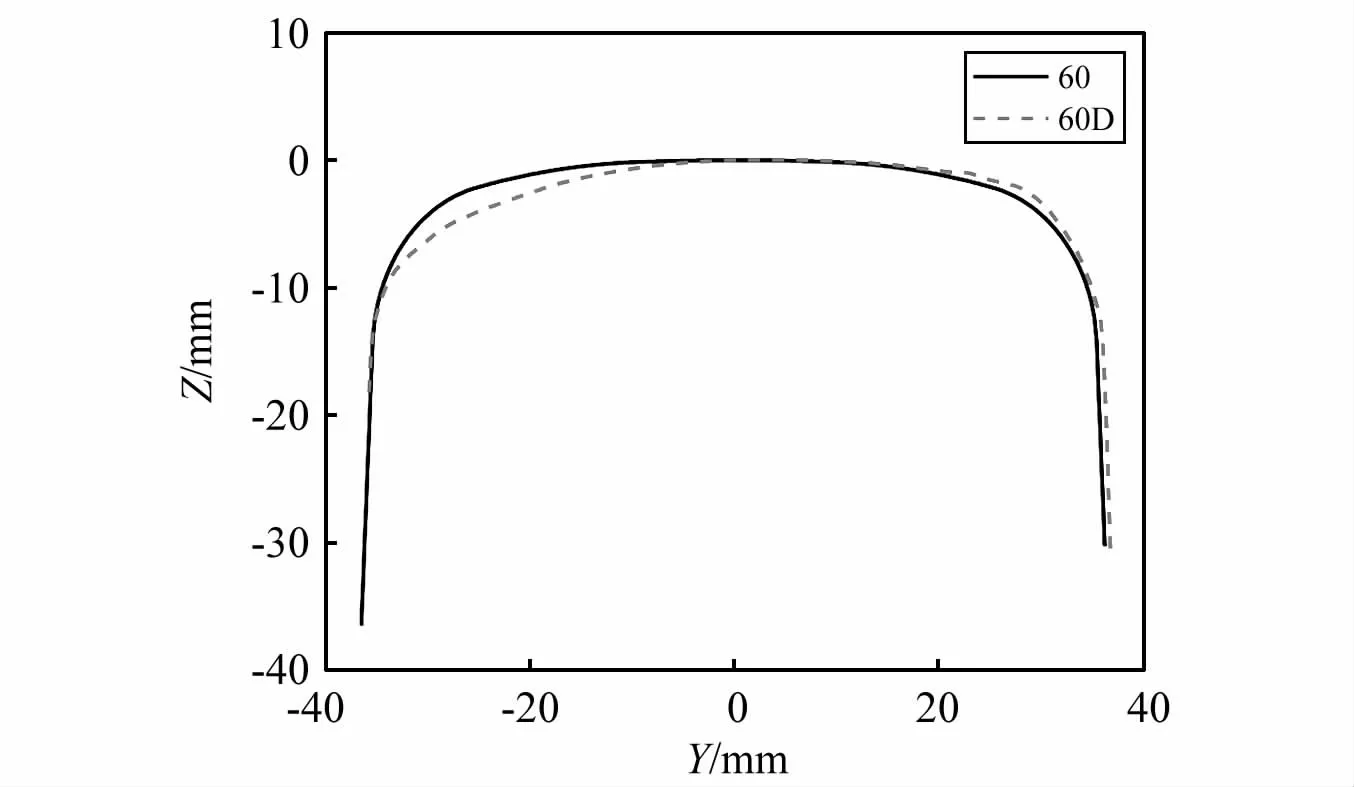
图13 60钢轨和60D钢轨廓形Fig.13 Profile of 60 rail and 60D rail

图14和图15给出了直线段和曲线段的横向和平稳性指标，可以看出，在直线段下，S1002CNopt踏面与60钢轨廓形和60D钢轨廓形匹配时横向平稳性均有所降低，优化后踏面与60D钢轨匹配时效果显著，最大降低0.56，垂向平稳性指标具有相似的规律。在曲线上时，两种踏面与60钢轨廓形接触时横向平稳性指标相差较小，与60D钢轨廓形接触时，优化后踏面降低了横向平稳性指标，在高速运行时效果显著，而垂向平稳性规律相似。

图14 直线平稳性标Fig.14 Ride index of straight track

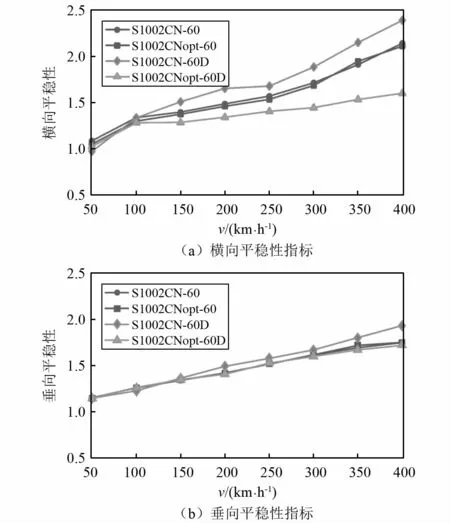
图15 曲线平稳性标Fig.15 Ride index of curved track

4.4 磨耗性能

磨耗计算时采用USFD模型计算，该模型基于R8T（车轮）和UIC60 900A（钢轨）两种轮轨材料通过实验所得，其模型的磨耗功可以表示为

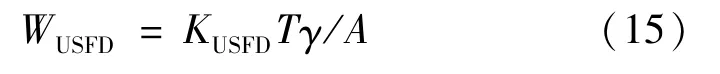
式中:A为接触斑面积，m2；KUSFD为磨耗系数；WUSFD为磨耗功。

KUSFD与Tγ/A的关系可以表示为轻微磨耗

严重磨耗

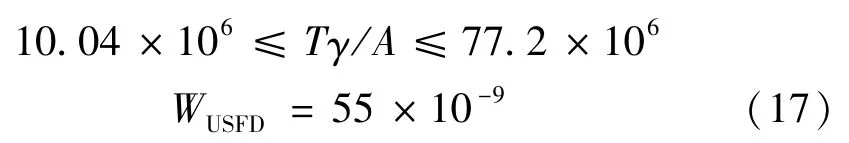
毁坏性磨耗

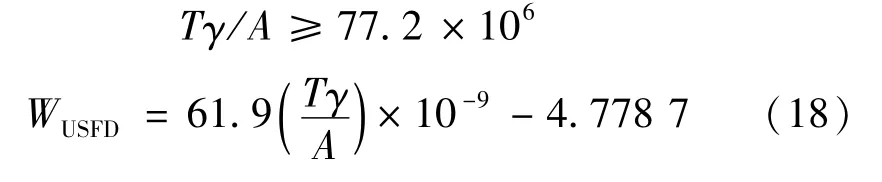
通过Fastrip计算剪切应力后，利用USFD模型可计算出接触斑每个网格上的磨耗功WUSFD。则磨耗体积 δp（t）（x，y）可以通过式（19）计算

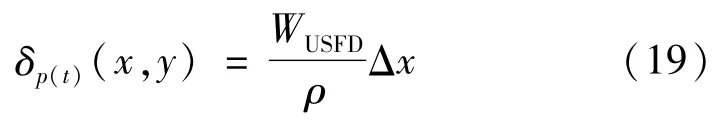
式中:ρ为材料密度，ρ=7 850 kg/m3；Δx为网格纵向宽度。

采用USFD磨耗模型对于两个踏面廓形进行磨耗预测仿真，磨耗计算过程中按照运营里程更新车轮踏面，每运行1万km更新一次踏面廓形。当运营里程达到16万km时，S1002CN型面和S1002Cnopt型面的磨耗深度，如图16所示。从图中可以看出，原始车轮型面磨耗深度为0.838 mm。优化后的S1002CNopt车轮型面最大磨耗深度为0.726 mm。因此，型面优化后可以有效减小车轮磨耗13.4%。

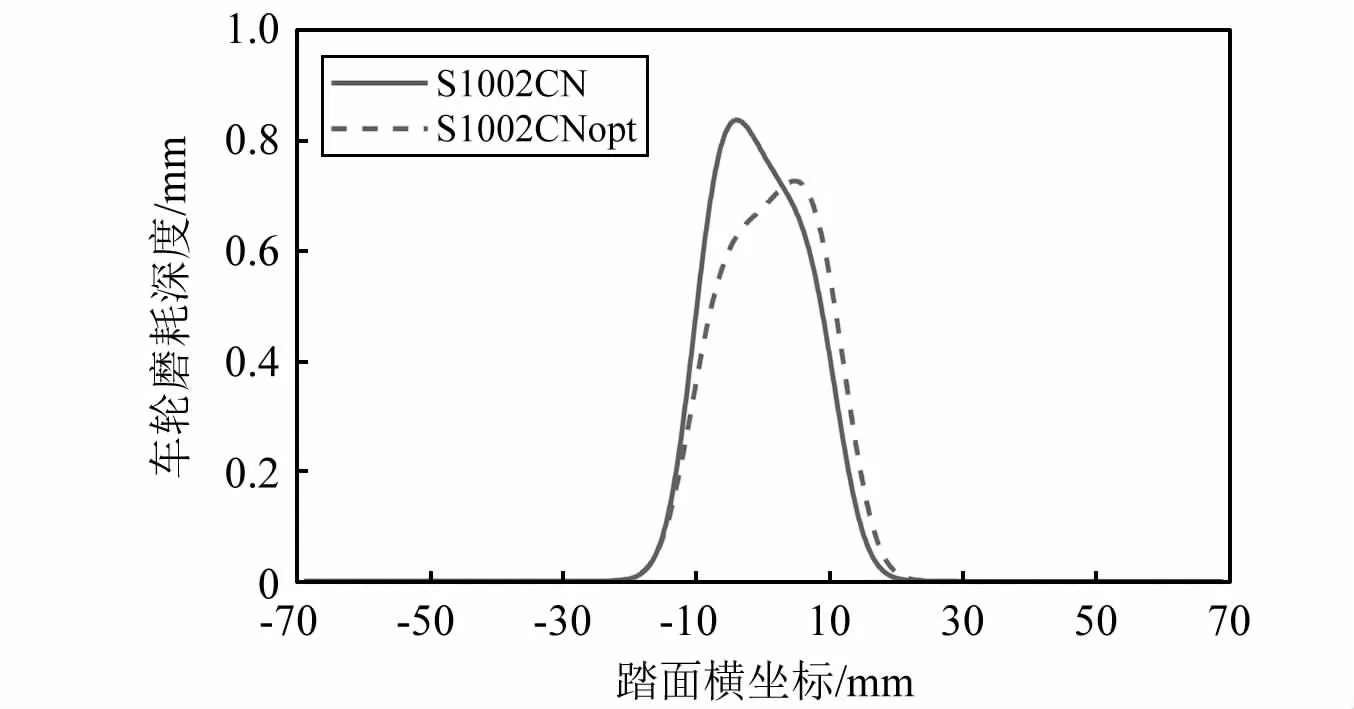
图16 车轮磨耗预测Fig.16 Wheel wear prediction

5 结 论

车轮型面设计主要包括了型面生成、动力学模型计算和型面优化三部分组成，本文通过采用以上步骤进行车轮型面优化，主要得到以下结论:

（1）本文采用旋转压缩微调法进行高速动车组型面生成，引入两个变量参数。该方法提高了踏面生成的效率，使车轮型面的工程适用性进一步增强。

（2）KSM-PSO算法用来优化出能够同时减少踏面磨耗和提高舒适度的型面S1002CNopt，优化后轮轨接触点分布更加均匀，轮轨接触班面积增大，轮轨最大接触应力减小。稳定性进一步提高，临界速度增大35 km/h，直线和曲线的横向平稳性进一步提高。当与60D钢轨型面匹配时其效果更加显著。

（3）利用USFD方法计算了运行15万km的磨耗深度，优化后的车轮型面S1002CNopt磨耗深度较S1002CN减小13.4%。该优化踏面其磨耗范围并未有效增大，实际运营中仍有可能产生磨耗集中的现象。下一步将考虑运营过程中踏面磨耗对于踏面设计的影响，以及进一步提高轮轨共形接触来进行车轮型面设计。