多类型源储协调互动的配电网分布鲁棒优化调度

尉耀稳，李跃龙，陈思超，杨波，周国华

(1.浙江中新电力工程建设有限公司，浙江 杭州 311201；2.中国电力科学研究院有限公司，江苏 南京 210009；3.国网浙江杭州市萧山区供电有限公司，浙江 杭州 311202)

0 引言

能源枯竭和环境污染是全人类共同面临的难题，光伏发电(photovoltaic,PV)、风力发电(wind turbine,WT)等可再生能源发电可以提供清洁的电能供应，在配电网中的渗透率不断提高[1—2]。同时，分布式储能系统(energy storage system,ESS)作为可再生能源消纳和利用的有效途径，近年来发展迅速[3]。可再生能源出力具有典型的随机性与不确定性，传统的确定性优化方法难以满足配电网安全运行需求，因此不确定性环境下配电网的优化调度成为当前研究热点[4—5]。

PV、WT以及ESS等源储资源具有不同的运行特性，对配电网中传统设备和多类型源储设备进行协调优化，可以有效提高配电网运行的安全性和经济性[6—8]。此外，考虑不确定性的配电网优化调度方法，主要以随机规划(stochastic programming,SP)[9—10]和鲁棒优化(robust optimization,RO)[11—14]为典型代表。文献[15]对SP理论及其应用进行了综述分析，文献[16]基于场景削减的SP构建了配电网多时间尺度优化模型。鉴于不确定变量的真实概率分布是复杂难获的，SP理论具有鲁棒性低的缺点。虽然已有研究通过调节风险度来提高SP的鲁棒性[17]，但由于通过假设或多个场景的不确定变量分布描述与实际情况具有较大差别，调节风险度的方法难以真正解决鲁棒性低的问题。

RO可以保证不确定变量在给定不确定集内任意变化时，始终满足系统安全约束。文献[18]利用两阶段RO方法进行储能系统和可控负荷的协调优化。文献[19]和[20]考虑PV不确定性，分别提出配电网鲁棒无功电压控制和无功补偿装置配置策略。然而RO具有较为明显的保守性缺点，文献[21]通过引入仿射运算来降低传统RO的保守度，但决策的保守度降低程度有限。为解决该问题，有学者提出了分布鲁棒优化(distributionally robust optimization,DRO)[22]方法，且已应用在大电网机组组合[23]、配电网无功优化[24—25]等相关研究中，有效降低了传统RO的保守度。

基于上述研究背景，文中充分考虑配电网的不确定性特征，挖掘PV、WT以及ESS等源储资源的协调互动潜力以及对配电网运行的有效支撑作用，提出配电网DRO调度方法，通过多类型源储资源的协调互动，提高了配电网中可再生能源的消纳与利用效率，实现了优化决策鲁棒性与保守度的平衡。

1 配电网确定性优化调度模型

1.1 辐射状配电网模型

配电网一般以辐射状或弱环状的方式运行，典型的配电网结构如图1所示。其中有载调压变压器(on load tap changer,OLTC)是配电网中的传统离散设备。在图1结构下，配电网支路潮流模型为：

图1 辐射状配电网结构Fig.1 Structure of radial distribution network

(1)

(2)

(3)

(4)

式中：Vi,t为节点i(i∈N)在t时刻的电压幅值，N为配电网中所有节点的集合；Pj,t，Qj,t分别为节点j(j∈N1)在t时刻的注入有功和无功功率，N1为平衡节点外所有节点的集合；ij为节点i与节点j之间的支路，且存在ij∈E，E为所有支路的集合；rij,xij分别为支路ij的电阻和电抗值；Iij,t为在t时刻从节点i流向节点j的电流幅值；Pij,t，Qij,t分别为在t时刻从节点i流向节点j的有功功率和无功功率。

1.2 调控设备模型

1.2.1 OLTC模型

OLTC通过调节档位进行变电站变压的控制，其运行模型为：

V1,t=V0(k0+αtΔk)

(5)

(6)

1.2.2 并联电容器模型

并联电容器(capacitor bank,CB)是配电网的离散无功补偿设备，通过电容器的投切对配电网进行无功支撑，CB的运行模型为：

(7)

(8)

(9)

此外，OLTC和CB还具有调度周期内最大动作次数限制，文中采用了文献[13]中相同的约束模型。

1.2.3 PV模型

PV是一种将太阳能转化为电能的新型发电系统，通过逆变器向配电网提供有功和无功支撑，其数学模型为：

(10)

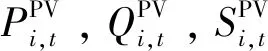
1.2.4 WT模型

WT利用风能进行发电，文中为分析不同类型可再生能源在不同运行模式下对配电网的支撑作用，分别对PV的无功功率和WT的有功功率进行调控。因此，WT的调控模型如下：

(11)

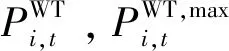
1.2.5 ESS模型

ESS既可以储存配电网中过剩的电能，又可以向配电网提供有功支撑，其数学模型如下所示：

(12)

(13)

1.3 多类型源储协调互动优化调度模型

文中所建多类型源储协调互动优化调度模型通过调用可控资源，提高配电网运行的经济性和安全性，其目标函数为系统有功网损和WT有功削减最低，具体如下：

(14)

式中：cLoss，cWT分别为系统网损和WT有功削减损失系数。式(14)即表示了配电网有功网损和WT有功削减的综合目标函数。

配电网运行应始终满足电压和电流安全约束，该约束如下所示：

(15)

(16)

由于CB、PV、WT以及ESS等设备的接入，配电网的有功和无功注入功率均发生变化，配电网节点有功和无功注入功率为：

(17)

(18)

鉴于式(2)中存在二次变量，上述模型为典型的非凸模型，为实现模型高效求解，引入二阶锥规划(second-order cone programming,SOCP)[19]理论，将原始的二次约束，即式(2)转化为凸的二阶锥约束，具体如下：

(19)

式中：lij,t，vi,t分别为支路电流、节点电压幅值的平方。此外，由于引入了节点电压幅值平方这一变量，OLTC约束即式(5)也转化为包含二次项的形式，其为非凸模型。文中采用文献[13]中的线性化方法，将上述模型转化为精确的线性化形式。

2 配电网DRO调度模型及求解

2.1 配电网DRO调度模型

可再生能源以及负荷均具有明显的不确定性，不确定变量的真实概率分布难以获取，基于概率密度进行不确定性刻画的SP鲁棒性不足。RO具有高鲁棒性的优点，但保守性较高，基于RO制定的优化运行决策往往经济性较差。因此，文中采用具有SP和RO优点的DRO方法，可在不确定性环境下确保决策较高的鲁棒性，同时有效降低传统RO决策的保守度。

DRO不需要不确定变量的真实概率分布，其基于历史数据，利用数理统级的方法对不确定变量的分布范围进行限制。假设基于历史数据获得K个实际运行场景，对该K个场景进行聚类分析可以获得L个离散场景，进而基于该离散场景获取不确定变量初始概率分布f0。考虑到f0并不是不确定变量的实际概率分布，因此引入基于1范数和无穷范数的置信度进行不确定变量的实际概率分布范围限制。假设不确定变量的实际概率分布为f，则该置信度可以表示为：

Pr{||f-f0||1≤θ1}≥1-2Le-2Kθ1/L

(20)

Pr{||f-f0||∞≤θ∞}≥1-2Le-2Kθ∞

(21)

(22)

(23)

式中：f，f0分别为不确定变量真实概率分布和初始概率分布；K，L分别为实际场景和聚类后的典型离散场景个数；α1，α∞分别为1范数和无穷范数的置信度系数，其限制了置信度的大小。置信度系数值越大，鲁棒性越强，相应的保守度也越高；反之，若该置信度系数越小，则优化结果的鲁棒性越差，相应的保守度也较低。基于该置信度系数，可以获取不确定变量的分布集合，具体如下：

(24)

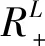
基于上述不确定变量概率描述，结合所建配电网确定性优化调度模型，建立多类型源储协调互动的配电网DRO调度模型。为方便表述，将其写成矩阵的形式，即：

(25)

约束为：

Ax≤b

(26)

Bys≤f

(27)

Cx+Dys=g

(28)

||Eys+H||2≤CTys+d

(29)

Hys=us

(30)

式中：x为第一阶段变量；ys为第二阶段决策变量；us为不确定变量的预测值；Ys为第二阶段变量可行域；A,B,C,D,E,H均为系数矩阵；a,b,c,d,e,f,g,h均为系数向量。式(25)表示所建配电网DRO调度模型的目标函数，其对应于式(14)；式(26)表示第一阶段决策变量不等式约束，对应于OLTC、CB以及ESS的动作及动作次数限制；式(27)表示第二阶段变量不等式约束，对应于PV、WT动作以及配电网安全约束；式(28)为等式约束，对应于潮流以及设备动作特性约束；式(29)为二阶锥约束；式(30)为不确定变量的离散化约束。

2.2 DRO模型求解

文中所建配电网DRO调度模型本质为包含不确定变量的min-max-min双层优化模型，文中引入了列和约束生成(column and constraint generation,C&CG)[24]算法，进行该模型快速求解。首先，原始的min-max-min问题被分解为一个min主问题和一个max-min子问题。其次，在max-min子问题中，max寻求不确定变量的最恶劣概率分布，而min寻求该最恶劣场景下第二阶段变量的最优解。再次，基于该最恶劣场景和第二阶段的最优解，通过求解min主问题获取全局最优解。在C&CG求解过程中，min主问题提供了一个原问题的下界解，而max-min子问题则提供一个上界解。随着迭代的进行，上界解和下界解之间的间隙不断减小，当该间隙小于收敛标准时，则算法收敛。

min主问题的本质为求取不确定变量最恶劣概率分布下的最优解，该主问题的模型为：

(31)

(32)

如前文所述，max-min子问题给出的是一个上界解，该子问题目标函数为：

(33)

式(33)所示的目标函数为一个max-min双层优化问题，难以直接求解。鉴于不确定变量集合Ψ与第二阶段决策值集合Y之间不存在直接的耦合关系，因此可以通过分解算法进行求解。同时，文中引入了0-1辅助变量zs+,zs-进行1范数约束的凸化，将其转化为凸约束的形式：

(34)

(35)

通过上述变换，该max-min问题可以被直接分解为一个max问题和一个min问题。首先对内存的min问题进行求解，然后将获取的解传递给外层的max问题，进而直接求解max问题。

综上，利用C&CG算法进行配电网DRO模型求解的流程如下所示：

(1)初始化。设置初始迭代次数k=1，初始下界值BL=0,初始上界值BU=+∞，设定收敛标准ε，给定不确定变量初始概率分布f0。

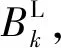
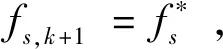
(5)返回迭代。设置k=k+1，并返回(2)，求解更新后的主问题。

3 算例分析

3.1 算例介绍

为了验证所提优化模型和算法的有效性与准确性，文中采用PG&E 69节点系统[13]进行仿真计算。该测试系统共有69个节点，其中包含68条支路。系统电压等级为12.66 kV,系统的有功负荷共计3 802.19 kW,系统无功负荷共计2 694.60 kvar。在该系统中，电压安全调节范围为[0.95,1.05]，同时安装了OLTC、CB、PV、WT以及ESS等设备，设备参数如表1和表2所示。

表1 OLTC、CB、PV、WT配置参数Table 1 The parameters of OLTC,CB,PV and WT

表2 储能配置参数Table 2 The parameters of ESS

考虑到有功负荷、无功负荷、PV以及WT出力的波动性和不确定性，其基础预测值如图2所示。基于该基础预测值，利用均值为0，方差为0.2倍预测值的标准正态分布生成10 000个历史运行场景。基于该10 000个历史场景，通过聚类获得10个典型场景，由于聚类过程不属于论文的研究重点，故其详细过程不进行赘述。算法中1范数的置信度参数α1设置为0.9，无穷范数置信度系数α∞设置为0.85。

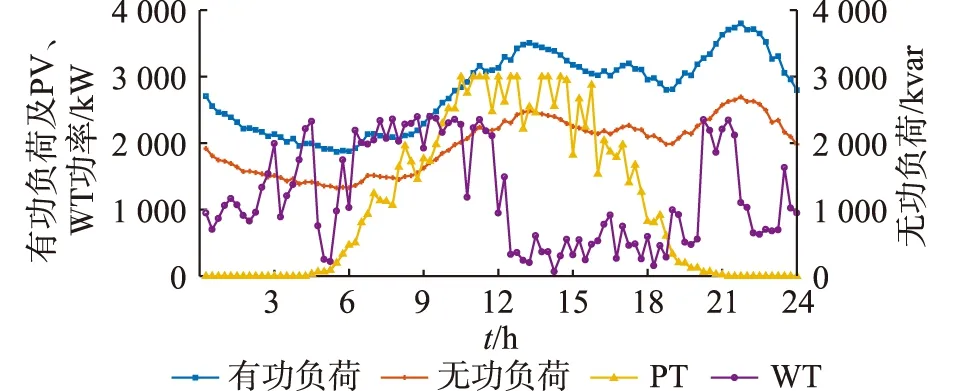
图2 24 h负荷、PV和WT基础出力预测Fig.2 The forecasted load,PV and WT power generation in 24 hours

3.2 结果分析

在文中所提配电网优化调度中，对OLTC、CB以及ESS的调度决策进行每小时的控制以提高系统运行的经济性，减少弃风现象，同时保证系统的运行安全。通过DRO模型求解，获取可控设备的控制决策，其中OLTC和CB的决策值如图3所示，ESS的决策值如图4所示。

图3 OLTC和CB档位决策Fig.3 Dispatch decision of OLTC and CBs

图4 储能控制决策和电量变化Fig.4 Control decisions and electric quantity of ESS

由图3和图4可知，在WT大量发出有功功率，同时负荷需求较低的时段(如07:00—10:00)，OLTC档位决策较低，表明变电站通过低档位来降低平衡节点电压幅值，从而实现对全网电压水平的调节以保障运行安全。相应地，在该时段ESS55处于充电的状态，从配电网中吸收过剩电能进行存储。在00:00—04:00，WT和PV提供的有功功率较低，各ESS均处于放电状态，为配电网提供有功功率支撑，通过减少总的潮流流动来降低系统网损。

分析图4可知，2个ESS系统的充放电状态并不完全同步，这是由其地理位置决定的，说明ESS可以实现本地可再生能源发电的有效消纳。在分布鲁棒的第二阶段，对WT有功出力和PV无功出力进行每15 min的调控，决策如图5和图6所示。

图5 PV无功功率决策Fig.5 Reactive power output of PVs

图6 WT有功功率调度决策Fig.6 Dispatch decisions of WT active power

分析图5和图6可知，在09:00—11:00，由于PV和WT均能够向配电网提供功率支撑，WT在调度周期内的削减幅度最高，同时ESS处于充电状态，从配电网中吸收电能进行存储。在负荷高需求的时段(20：00—23：00)，PV向配电网注入大量的无功功率进行电压调节，同时WT的有功功率削减也处于调度周期中的最低状态。分析图6可知，由于ESS的有效充放电，WT的削减幅度较低，表明了ESS在促进可再生能源消纳方面的积极作用。为验证所提方法在降低系统网损方面的有效性，将优化前后系统的网损进行了对比，如图7所示。

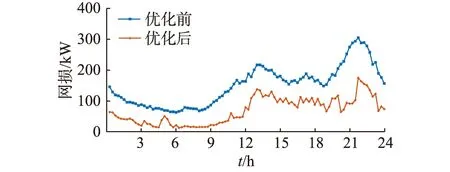
图7 优化前后系统网损对比Fig.7 The comparison of power losses between optimized and without optimized

分析图7可知，优化后系统的网损明显降低，优化前系统的平均网损是151.26 kW,优化后系统网损为69.96 kW,降损率达53.75%。通过多类型源储协调互动可以有效降低配电网运行网损以及WT有功削减，从而提高配电网运行的经济性，促进可再生能源消纳。同时，由于DRO策略考虑了WT、PV以及负荷需求的不确定性，因此其可以有效提高配电网运行的安全性。

4 结语

文中针对PV、WT以及ESS广泛接入的配电网，提出多类型源储协调互动的优化调度方法，通过协调优化OLTC、CB、PV、WT以及ESS，降低系统运行有功网损和WT有功削减，同时提高配电网运行安全性。考虑不同调节设备的动作特性，建立基于SOCP的两阶段优化调度模型，保证模型的凸特性以进行快速求解。在此基础上，计及PV、WT以及负荷需求的不确定性，引入了一种兼具高鲁棒性和低保守度的DRO理论，建立DRO调度模型，并通过C&CG算法进行求解。

算例分析表明所提方法可以有效提高配电网运行经济性，同时保障不确定性环境下的系统运行安全。此外，ESS通过合理的充放电可以有效降低WT的功率削减，提高可再生能源消纳和利用效率。文中所提DRO方法对不确定性优化问题，如微电网的能量管理有较强的借鉴意义。