基于解析法的电-热互联综合能源系统概率潮流计算

李红，王文学，伏祥运，何维祥，王炜，袁斌，王舒捷

(国网江苏省电力有限公司连云港供电分公司，江苏 连云港 222000)

0 引言

区域综合能源系统以电力系统为核心，综合考虑电、气、热等多种用能需求，形成具有多能协同特征的综合系统[1—4]。但目前电力系统、热力系统等普遍存在独立规划、独立运行的特点，各种能源网络间缺乏有效交互，难以发挥多能源系统的耦合互补的优势[5—7]。电-热系统稳态潮流属于确定性分析，是对综合能源系统深入研究的基础。综合能源系统稳态潮流主要从模型和求解方法两方面进行研究：在模型方面，电网稳态潮流方程是由节点功率方程组成的非线性方程组[8]。气网稳态模型包括管道流量方程、加压站方程和节点流量平衡方程[9]。热网稳态模型主要包括水力模型和热力模型[10]。目前主要利用牛拉法求解非线性方程组，一般分为统一求解和顺序求解[11]。

随着新能源的大量并网，负荷的不确定性增大，同时能源转化设备应用日益广泛，增强了不同能源系统间的耦合程度，因此综合能源系统包含大量不确定性因素[12]，如各类负荷或新能源出力的波动、故障等，且不同能源网络之间存在相互影响，某网络的波动可能造成综合能源系统潮流分布产生根本性的变化[13]。仅通过确定性分析难以把握综合能源系统在不确定环境下的运行状态，概率潮流能够充分考虑这些不确定性因素，从而更全面地反映系统运行状况。

目前，概率潮流的求解方法一般包括模拟法、解析法和近似法。模拟法中常用蒙特卡洛法，通过生成大量场景，寻找状态量的概率信息[14]，文献[15]提出一种电-热互联系统概率潮流计算方法，定量评估电转热技术对系统概率潮流影响。解析法中常用的是半不变量法[16—17]，文献[18]提出一种基于多点线性半不变量法的电-热互联系统概率潮流计算方法，定量得到相关状态量的概率信息。近似法中常用点估计法，优点为无需求解输入输出的具体关系，但相比其他2种方法，计算精度一般较低[19]。文献[20]提出一种计及相关性的电-气-热综合能源系统概率最优能量流计算方法，并采用基于Nataf变换的三点估计法对该模型进行求解。

热网方程具有强非线性，以往半不变量法将状态量描述为关于电-热负荷的线性方程，一般无法同时满足计算复杂度、精度和计算速度的要求。文中基于解析法和近似法，提出一种辐射状供热网络概率潮流快速计算方法，将状态量描述为关于电-热负荷的非线性方程，可直接获得管道流量和节点温度的概率信息，显著提高了计算速度和求解精度。

1 热网模型

1.1 热网非线性模型

热网模型包括水力模型和热力模型[21]，水力模型包括流量平衡方程和管道压降方程：

Am=mq

(1)

hf=Km|m|

(2)

式中：A为系数矩阵；m，mq分别为管道流量向量和热负荷流量向量，kg/s；hf为环路管道压降组成的向量，m；K为环路管道阻尼系数组成的向量；|m|为管道流量的绝对值。

热力模型包括热负荷方程、管道温降方程和热功率守恒方程。

Φ=Cpmq(Ts-To)

(3)

Tend=(Tstart-Ta)e-λL/(Cpm)+Ta

(4)

Tout∑mout=∑(minTin)

(5)

式中：Φ为热负荷向量，MW；Cp为水比热容，且Cp=4 182 J/(kg·℃)；Ts，To分别为节点供水温度向量和回水温度向量，℃；Tstart，Tend，Ta分别为管道首端温度、管道末端温度和环境温度，℃；λ为传热系数，W/(m·K)；L为管道长度，m；min，mout分别为注入节点流量向量和流出节点流量向量，kg/s；Tin，Tout分别为流入节点温度和节点混合温度，℃。

热网方程式(1)—式(5)中含有指数方程，非线性程度较高，且管道流量与节点温度为乘积关系，耦合程度较高。目前常采用牛顿法求解稳态潮流，计算较为复杂，甚至可能存在不收敛等问题。

1.2 电热耦合元件模型

热电联产机组分为定热电比机组和变热电比机组2种，分别用式(6)和式(7)表示。

Cm=ΦCHP/PCHP

(6)

Cz=ΦCHP/(ηeFin-PCHP)

(7)

式中：Cm，Cz分别为机组的定热电比和变热电比；ΦCHP，PCHP分别为机组的热出力和电出力；ηe，Fin分别为机组的冷凝效率和燃料输入速率。

1.3 辐射状热网概率潮流模型

两节点供热网络如图1所示，图中TH，TH1，TH2分别为热源温度、节点1温度和节点2温度；mH为热负荷流量。利用管道温降方程式(4)与热负荷功率方程式(3)推导[22]可得式(8)。

图1 两节点供热网络Fig.1 District heating network with two nodes

(8)

式中：TR为热负荷回水温度；Φ2为节点2的热负荷。将式(8)推广至多根管道，如式(9)所示。

(9)

多节点供热网络如图2所示，对于含有分支的节点，此时m1≠m2≠…≠mi，其中m1，m2，…，mi-1为管道流量，mi为热负荷流量。

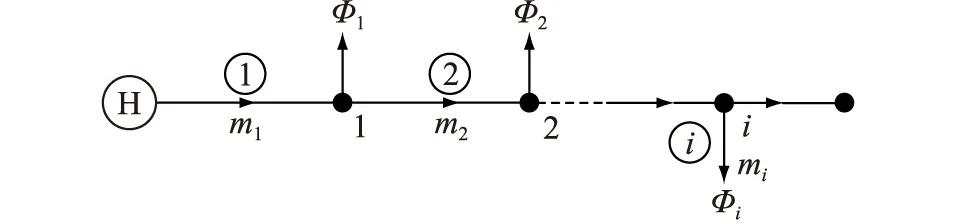
图2 多节点供热网络Fig.2 District heating network with multiple nodes

图2中，引入变量n1，n2，…，ni，令n1=m1/mi，n2=m2/mi，…，ni-1=mi-1/mi，ni=mi/mi=1，代入式(10)可得mi为：

(10)

由于潮流计算前管道流量未知，令：

(11)

式中：k为热负荷流量mi经过的干路管道编号；Φi为节点i的热负荷；Qk为管道k所流入热能的期望值，因此n1，n2,…,nk将为定值[22]。

因此，由随机变量的数字特征，mi的均值和方差可表示为：

(12)

(13)

式中：E(mi)为管道i中热负荷流量mi的均值；D(mi)为管道i中热负荷流量mi的方差。由于比热容Cp=4 182 J/(kg·℃)，则当式(12)中ni为定值时误差较小，因此由热负荷的均值和方差可得管道流量的均值和方差。将热负荷功率方程式(3)代入式(10)，移项变形可得式(14)。

(14)

再由随机变量的数字特征可得：

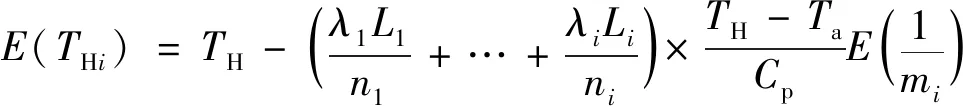
(15)

(16)

由式(15)、式(16)可知，得到流量倒数的均值和流量倒数的方差后，可获得节点温度THi的均值与方差。设正态分布随机变量x=mi的均值和标准差分别为μi，σi，其概率密度函数为：

(17)

由连续型随机变量的概率密度函数性质可知，y=1/x=1/mi，概率密度函数为：

(18)

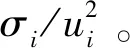
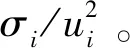
综上所述，由式(12)和式(13)可得供热网络管道流量的均值与方差，由式(15)—式(18)可得节点温度的均值与方差。求得热电联产(combined heating and power，CHP)热出力概率分布后，由机组热出力与电出力关系可得机组电出力概率分布，进而求得电网中各状态变量的概率分布。

2 辐射状热网概率潮流算例测试

23节点辐射状热网算例如图3所示，CHP源温度恒定为80 ℃，负荷节点回水温度恒定为45 ℃，环境温度Ta为10 ℃，测试采用Matlab编程，仿真环境为1.9 GHz CPU，4.0 GB RAM的PC机。

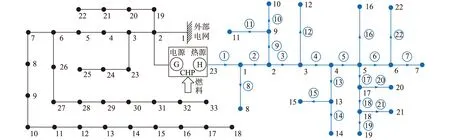
图3 电-热互联综合能源系统Fig.3 The diagram of combing electricity and heat networks

2.1 典型状态量的均值与方差

若每根管道长度设置为500 m，所有负荷节点热负荷均设置为0.5 MW，热负荷波动均在±10%以内。文中方法和蒙特卡洛法所得流量均值、流量标准差分别为μm，σm，μm,mcs，σm,mcs；流量均值误差百分数、流量标准差误差分别为δμ,m，δσ,m。因此有:

δμ,m=(|μm-μm,mcs|/μm,mcs)×100%

(19)

δσ,m=|σm-σm,mcs|

(20)

温度均值、温度标准差分别为μT，σT，μT,mcs，σT,mcs；温度均值误差百分数、温度标准差误差分别为δμ,T，δσ,T。因此有：

δμ,T=(|μT-μT,mcs|/μT,mcs)×100%

(21)

δσ,T=|σT-σT,mcs|

(22)

其中蒙特卡洛结果是采用热网非线性模型计算所得，采样20 000次。此时计算出的流量和温度的均值与标准差如表1和表2所示，文中方法耗时0.019 6 s，蒙特卡洛法耗时1 720.105 4 s。

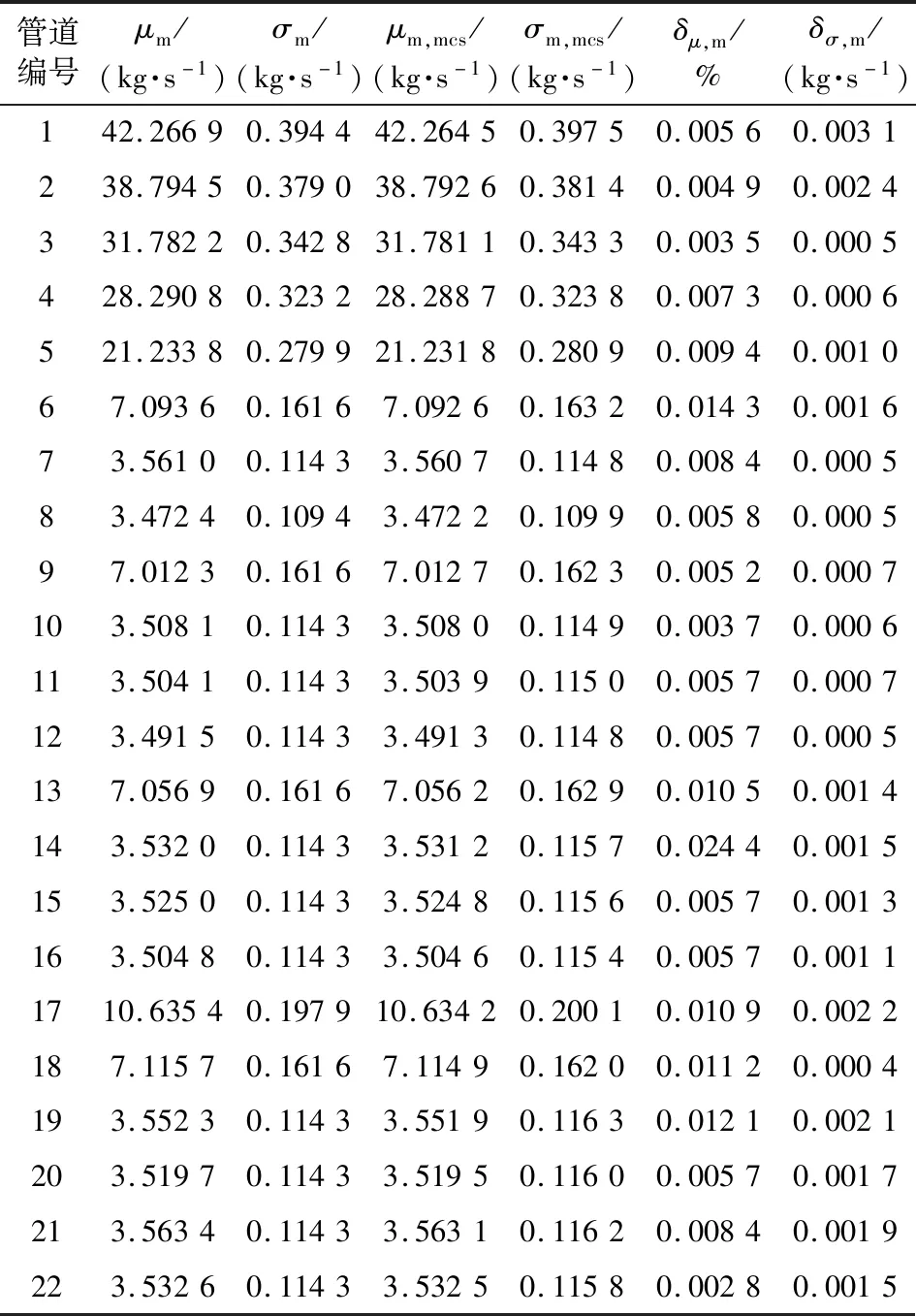
表1 所有管道流量均值和标准差的比较Table 1 Comparison of mean and standard deviation of all pipe flow

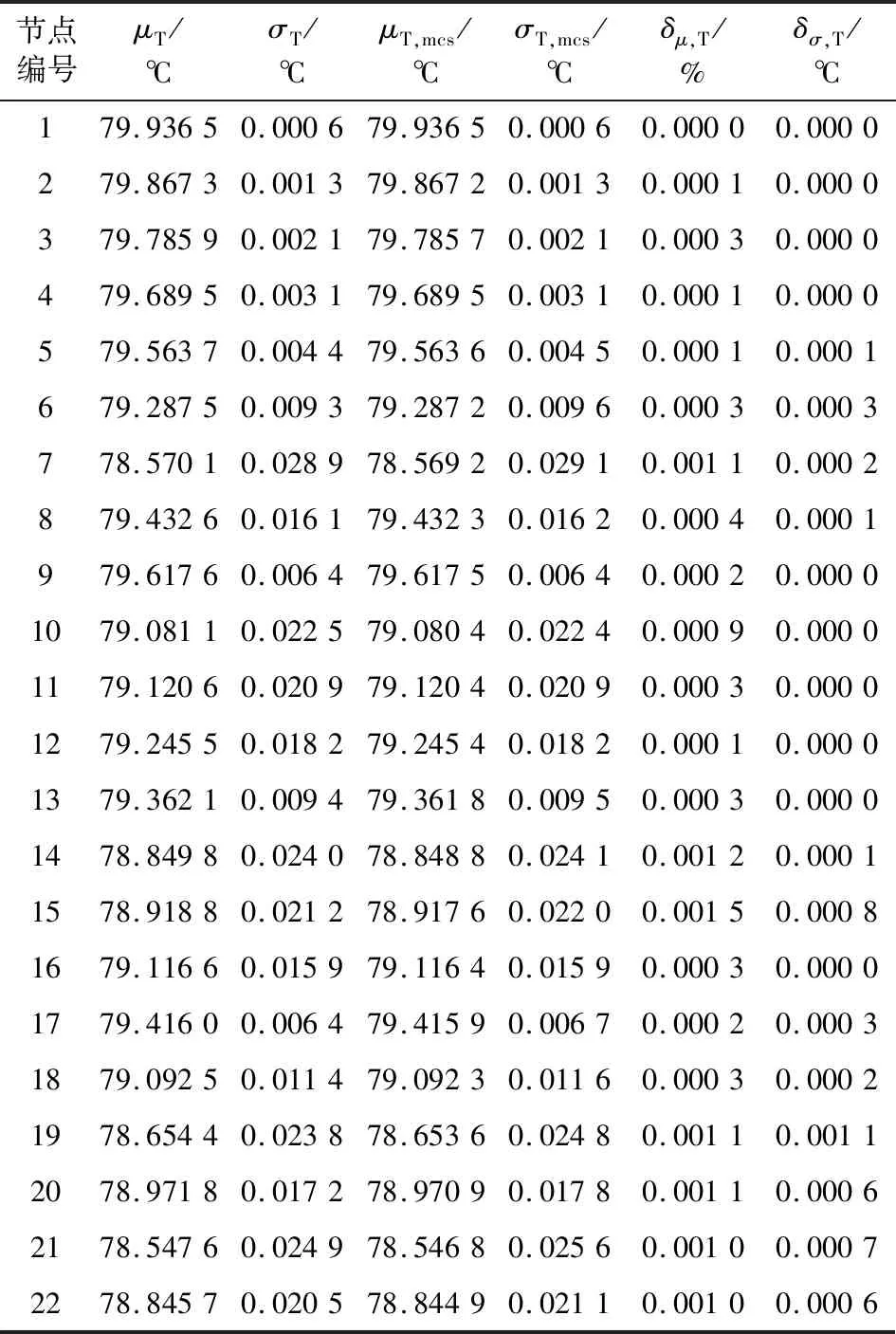
表2 所有节点温度均值和标准差的比较Table 2 Comparison of mean and standard deviation of all node temperatures

由表1可知，管道流量均值误差百分数最大值为0.024 4%，平均值为0.008 0%，管道流量标准差误差最大值为0.003 1 kg/s，平均值为0.001 3 kg/s。由表2可知节点温度均值误差百分数最大值为0.001 5%，平均值为0.000 5%，节点温度标准差误差最大值为0.001 1 ℃，平均值为0.000 2 ℃。可见文中方法具有较高的计算精度和计算速度。

由表1可知，文中方法和蒙特卡洛法所得管道1的流量均值分别为42.266 9 kg/s和42.264 5 kg/s，2种方法求得的热源节点回水温度均值均为44.712 2 ℃，由式(3)计算可得热源的热出力相差354.176 9 W，若式(6)中定热电比取1.3，则2种方法求得的热出力误差引起的电压和相角误差分别如图4和图5所示。

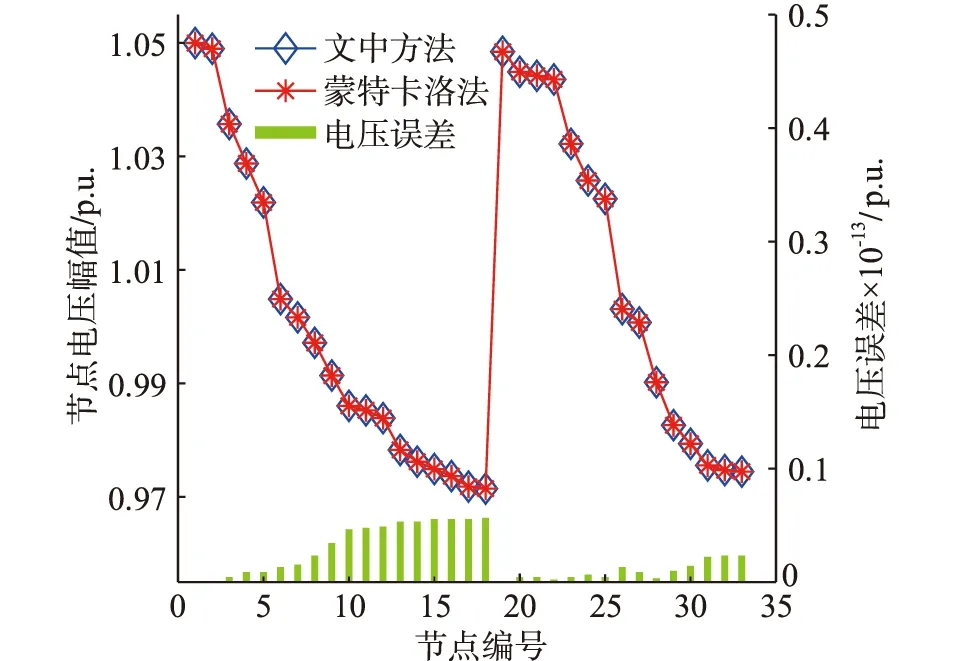
图4 热出力误差引起的电网电压误差Fig.4 Error of voltage amplitude caused by thermal output

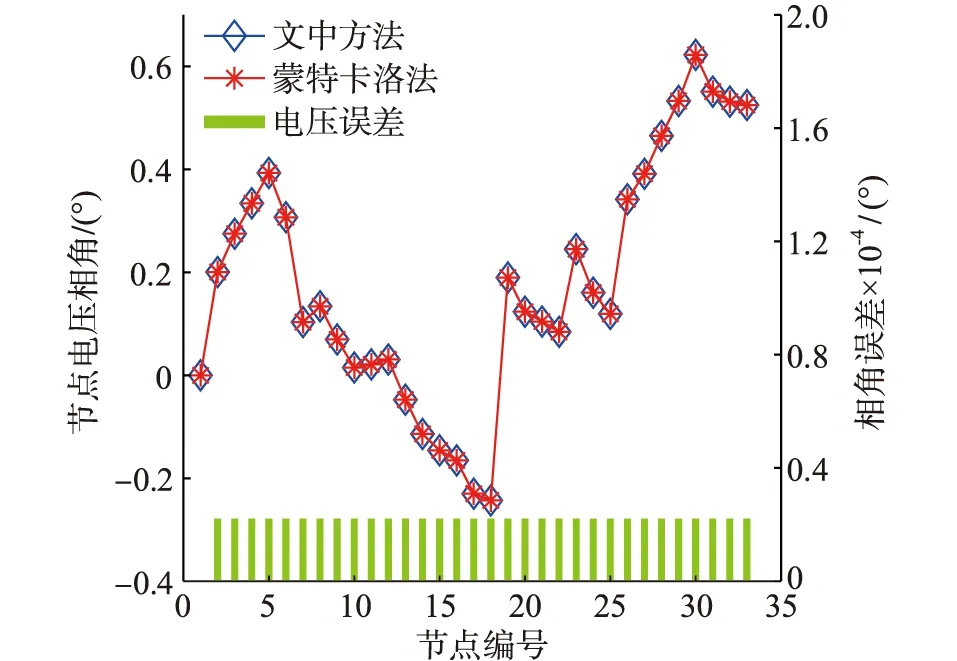
图5 热出力误差引起的电网相角误差Fig.5 Error of voltage phase angle caused by thermal output

由图4和图5可知，文中方法和蒙特卡洛法引起的电网电压误差和相角误差极小，表明文中方法产生的误差对电网影响极小，验证了该方法的有效性与合理性。

2.2 控制变量法

(1)设置每个负荷节点热负荷均为1 MW，所有热负荷波动量为±10%且保持不变，逐渐同时增大每根管道长度，节点19温度标准差见图6(节点19温度标准差误差最大)。

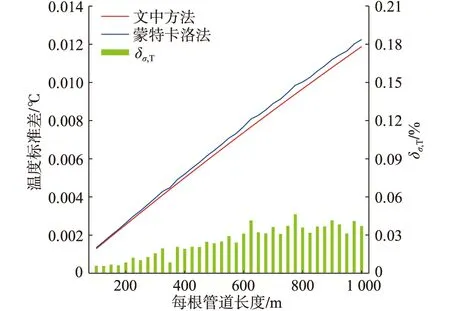
图6 节点19温度标准差随管道长度变化情况Fig.6 The temperature standard deviation of node 19 varying with the length of the pipeline

由图6可知，节点19温度标准差与管道长度近似呈线性正相关，且δσ，T小于0.05%。

(2)设置每根管道长度为500 m，热负荷波动量为±10%且保持不变，逐渐同时增大每个负荷节点热负荷值，节点19温度标准差如图7所示。

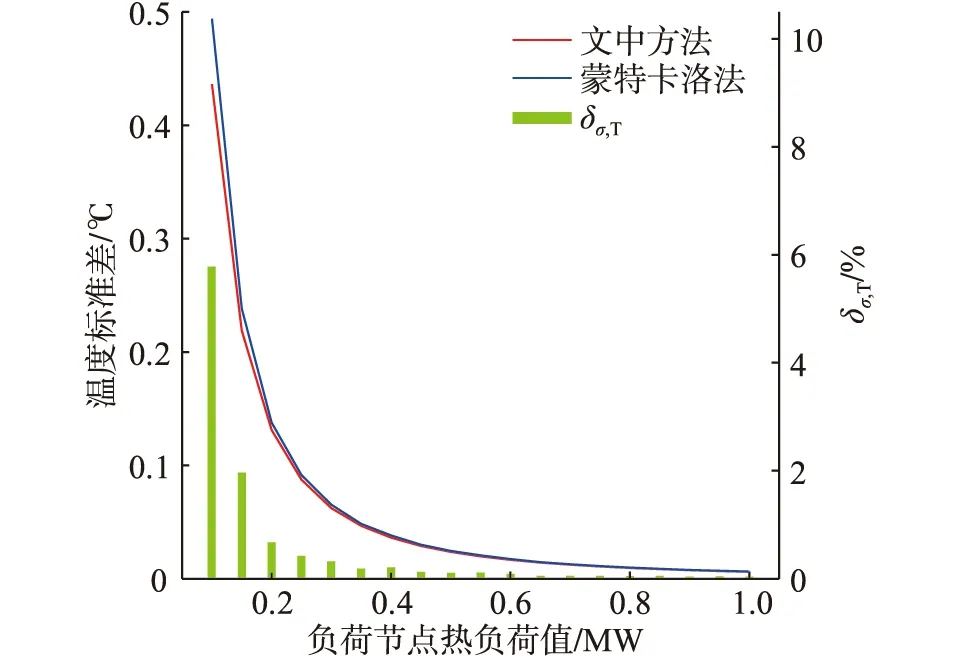
图7 节点19温度标准差随热负荷值变化情况Fig.7 The temperature standard deviation of node 19 varying with the heat load value

由图7可知，节点19温度标准差与热负荷值呈负相关，且曲线的切线逐渐平缓，热负荷值对节点温度标准差的影响相对较大。同时，随着热负荷值的增大，文中方法的误差逐渐缩小，当热负荷值为1 MW时，节点19温度标准差误差小于0.02%。

(3)设置管道长度为500 m，热负荷为1 MW且保持不变，逐渐同时增大热负荷波动量，节点19温度标准差如图8所示。

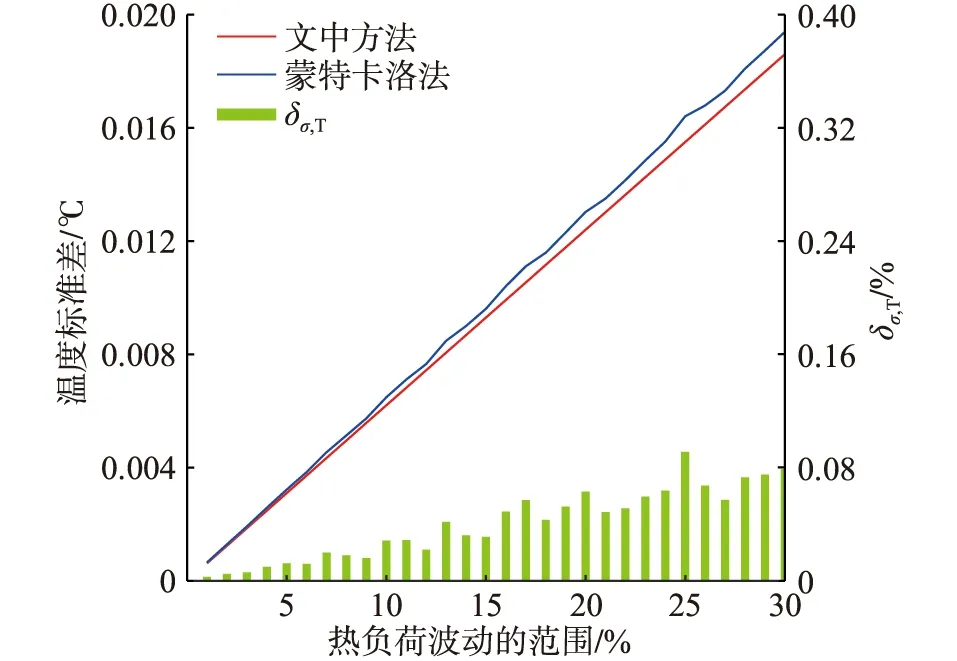
图8 节点19温度标准差随热负荷波动量变化情况Fig.8 The temperature standard deviation of node 19 varying with the fluctuation of heat load

由图8可知，节点19温度标准差与热负荷波动量近似呈线性正相关，且δσ，T小于0.1%。

2.3 典型状态量的三维关系图

设置热负荷波动量为±10%，当改变管道长度和热负荷值时，采用蒙特卡洛法所得管道1流量标准差和节点19温度标准差分别见图9和图10。

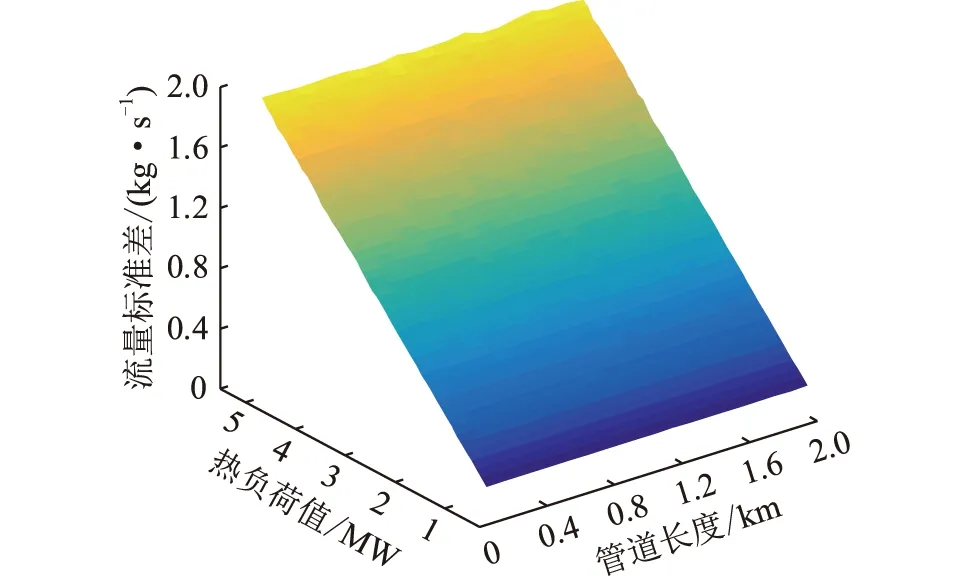
图9 管道1流量标准差与管道长度和热负荷的关系Fig.9 The relationship among the flow stand-ard deviation of pipe 1,the pipe length and heat load value

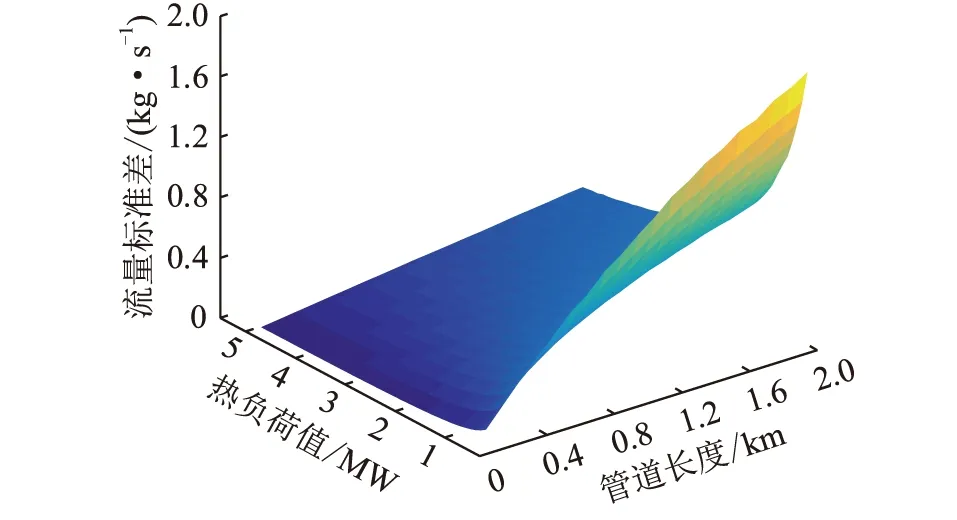
图10 节点19温度标准差与管道长度和热负荷关系Fig.10 The relationship among the temperature standard deviation of node 19,the pipe length and heat load value

由图9可知，管道长度与流量标准差没有呈现相关性，热负荷值与流量标准差近似呈线性正相关。由图10可知，管道长度与节点温度标准差呈正相关，而热负荷值与节点温度标准差呈负相关。

3 结论

文中提出了一种辐射状供热网络概率潮流快速计算方法，可同时获得热力网的稳态潮流与概率潮流，无需迭代，计算准确度高且不存在收敛性问题，结论如下：

(1)管道长度与流量标准差没有呈现相关性，管道流量标准差与热负荷值近似呈线性正相关。

(2)节点温度标准差与热负荷波动量近似呈线性正相关，节点温度标准差与管道长度近似呈线性正相关，节点温度标准差与热负荷值呈负相关。

(3)文中方法引起的热源热出力误差对电网电压和相角的影响极小。

文中方法在保证计算精度的同时，极大地提高了计算速度，可为综合能源系统不确定性分析提供参考。下一步将研究大规模可再生能源并网对电-热互联综合能源系统概率潮流的影响。

本文得到国网江苏省电力有限公司连云港供电分公司伏祥运劳模创新工作室2021年研究项目“电-热互联综合能源系统快速潮流计算方法与优化调度方法技术的研究与应用”(B110D02188D7)资助，谨此致谢！