数字微镜器件超分辨成像光学系统装调误差影响研究

邢思远，王 超，徐 淼，李英超*，史浩东，刘 壮，付 强

（1.长春理工大学空间光电技术吉林省重点实验室，吉林长春130022；2.中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033；3.长春理工大学光电工程学院，吉林长春130022）

1 引 言

超分辨成像方法是通过成像系统获得的单帧或多帧低分辨率图像得到高分辨率图像的一种技术[1]。在众多超分辨成像方法中，基于信号稀疏性原理的压缩感知算法因其优秀的超分辨性能成为了近年的研究重点[2]。

文献[3-4]通过引入稀疏训练字典的方式提升了压缩感知在超分辨成像中的效果和性能。压缩感知理论追求的是输入数据量的最小化，而这个理念与超分辨成像中利用低分辨率图像重建高分辨率图像的理念相近，这里低分辨率图像可以理解为被“压缩”后的数据[5]。由于压缩感知理论与超分辨成像理念的高度契合，使得目前大多数对于超分辨成像技术的研究都是基于压缩感知理论的重建算法，然而却忽略了光学系统本身对超分辨重建结果的影响。文献[6]针对编码孔径成像光谱仪系统中光路多次反射引起的光轴失准问题，提出利用激光参考定位和光的折反射原理相结合的方法进行装调。文献[7]中针对DMD与CCD像素对准时的漏光问题、实际观测与仿真模拟之间的误差以及特定镜头对超分辨成像结果的影响3个方面进行分析，提出了特定的重建模型，从而提高了图像重建质量。然而，上述文献都忽略了光学系统本身的误差对超分辨成像结果的影响。本文首先建立了DMD超分辨成像光学系统的成像模型，设计了一个长波红外波段的DMD超分辨成像光学系统，然后对超分辨成像光学系统的成像过程进行仿真研究，并提出了装调误差对超分辨成像质量影响的分析方法，在DMD成像光学系统的成像模型中分别引入适当的偏心、倾斜、镜片间隔误差、离焦等装调误差，对重建结果进行分析，得到了该DMD超分辨成像光学系统装调时的公差范围。

2 DMD超分辨成像光学系统基本成像模型与仿真过程

图像模糊退化过程一般可视为一个线性空间不变的退化系统。退化后的图像可表示为原始清晰图像与模糊核函数的卷积：

式中， (x,y)表 示模糊图像坐标，b(x,y)表示模糊图像，i(x,y)表 示原始清晰图像，“∗”表示卷积算符，k(x,y)表 示模糊核函数，n(x,y)表示加性噪声[8]。

对于光学图像退化过程，可认为引起图像模糊的模糊核函数k(x,y)是光学系统的点扩散函数。光学模糊退化过程一般可视为一个线性空间变化的退化过程，模糊图像可表示为：

式中，(s,t)表示原始清晰图像的坐标，ks,t表示空间变化的点扩散函数[9]。

在仿真过程中使用原始图像与光学系统的点扩散函数卷积模拟光学系统的成像过程，本文在仿真时，忽略了噪声的影响，仿真流程图如图1所示。

图 1 仿真流程图Fig. 1 Simulation flow chart

仿真过程在Matlab软件平台上实现，仿真过程主要包括5个步骤。

(1)将分辨率为640 pixel×512 pixel的场景与成像物镜的点扩散函数(Point Spread Function,PSF)做卷积，模拟成像物镜的成像过程。获取成像物镜的PSF时，在ZEMAX中可以直接提取所设置的9个视场的PSF矩阵，提取PSF矩阵时应保证PSF的数据采样间隔与探测器像元尺寸相同，DMD超分辨成像光学系统设置的视场如图2所示。将所提取的9个视场的PSF按视场顺序进行拼接，将PSF矩阵的中心点坐标与视场点对应，即可获得不同视场位置的PSF。根据所提取的9个视场的PSF，再通过插值求取未知视场的PSF，以获取空间变化PSF。

图 2 视场设置Fig. 2 Field of view settings

所用的方法为基于主元分析的未知视场PSF插值获取方法，这种获取PSF模型的基本思想是寻找一组基函数，使得成像系统的PSF能够在由这组基函数所组成的函数空间内找到一个很好的近似。基于主元分析的PSF获取方法包括3个步骤：①已知点PSF的表征，选取主成分分析（PCA）模型表征PSF，拟合获取已知点的PSF主元分析模型参数；②利用点插值法获取未知点的PSF的模型参数；③未知点PSF的回归；将插值获取的参数带入PSF表征模型中拟合获取未知点PSF[10]。引入装调误差后，各视场PSF均发生变化，重复上述步骤即可获得引入装调误差后空间变化的PSF。

(2)将得到的图像与DMD编码模板进行叠加，对图像进行编码调制，通过DMD的4 pixel×4 pixel区域对应长波红外探测器的1 pixel，实现4倍分辨率的图像重构，采用的编码为随机伯努利矩阵，首先生成16个4 pixel×4 pixel的随机伯努利矩阵，再将其扩展平铺为640 pixel×512 pixel的矩阵，并与卷积后的图像进行点乘以实现对图像的编码。

(3)将编码后的图像与投影物镜的PSF卷积，仿真模拟投影物镜成像过程，投影物镜的PSF获取方法同上。

(4)将得到的640 pixel×512 pixel的图像降采样为160 pixel×128 pixel，仿真模拟低分辨率长波红外探测器成像过程。

(5)通过复原算法将16幅分辨率为160 pixel×128 pixel的图像重构为640 pixel×512 pixel的图像，实现4倍分辨率的图像重构。

采用的重构算法为正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)，采用 OMP 算法进行信号重构时，需要从信息算子中找到能够表示稀疏信号的一些最优原子，使得表示信号与测量值之间的残差最小，即不断逼近测量值的真实支撑集[11]，其详细计算过程可以参考文献[12]。将峰值信噪比(Peak Signal to Noise Ratio, PSNR)作为图像的客观评价指标。PSNR是使用最为广泛的一种图像客观评价指标，它基于对应像素点间的误差进行评价，一般用于最大值信号和背景噪声之间的一个工程项目。PSNR的单位是dB，其值越大表示失真越小，PSNR低于20 dB时图像不可接受。其计算过程为：

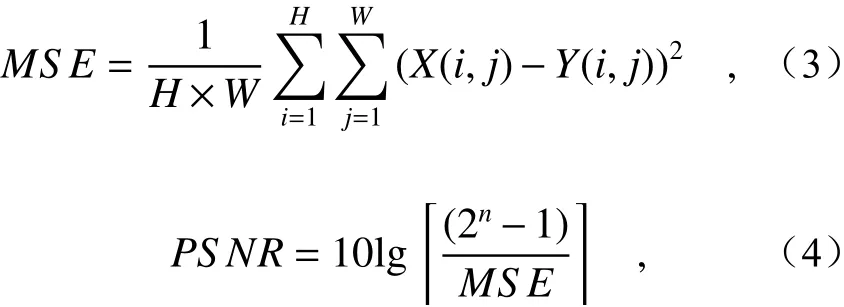
式中，MSE表示当前图像X和参考图像Y的均方误差(Mean Square Error)，H和W分别为图像的高度和宽度，n为每像素的比特数，一般取8，即像素为256灰阶。

图3 给出了原图和使用OMP算法重构得到的图像，最终重构图像的PSNR值为23.8302。

图 3 （a）原图和（b）OMP重构图像Fig. 3 (a) Original image and (b) OMP reconstructed image

3 基于DMD的超分辨成像光学系统

3.1 基于DMD的超分辨成像光学系统结构

根据上述DMD超分辨成像光学系统的基本成像模型，设计了一个基于DMD的超分辨成像光学系统。

DMD本质是一个反射式数字半导体光分布调制器[13]。在由半导体硅片做衬底的CMOS存储芯片上用铰链结构构建数以百万计的微反射镜面，利用静电使每个微镜面发生独立偏转，控制图像灰度等级[14]。

将DMD作为编码孔径掩模放置在系统的光学一次成像面上，前端编码元件与后端数据处理系统相配合，构成一种光学——数字计算混合成像系统。

所设计的光学系统主要由目标源、成像物镜、DMD、投影物镜、长波红外探测器等5部分组成，由成像物镜将目标景象成像在一次像面DMD上，中间像经DMD调制后通过投影物镜最终成像在长波红外探测器上。最终光学系统的总体构成如图4所示，主要技术指标如表1所示。

图 4 光学系统总体构成Fig. 4 Overall structure of the optical system

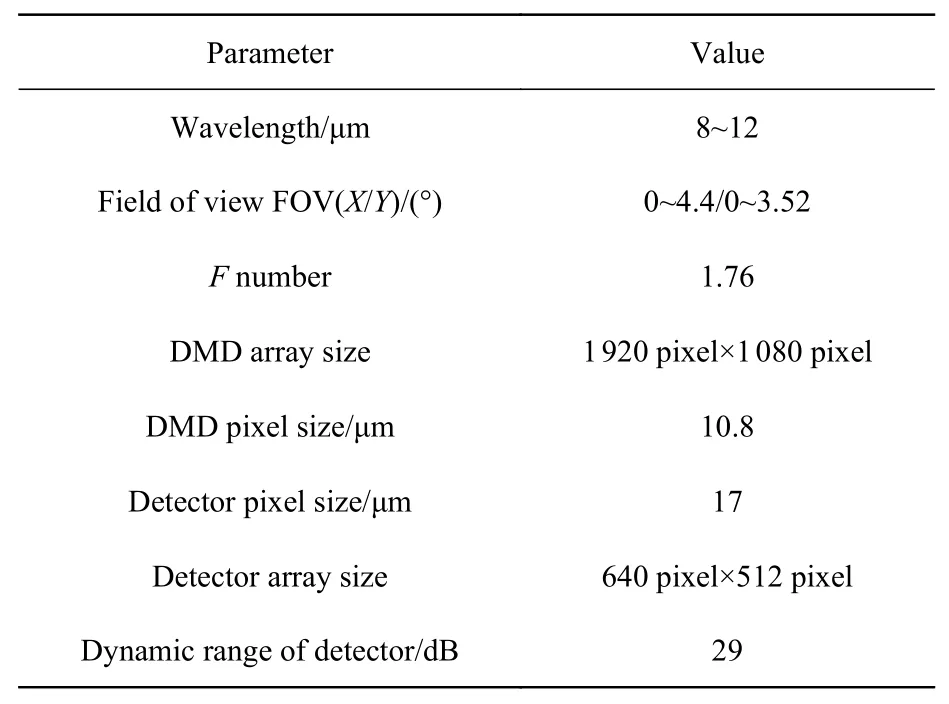
表 1 光学系统参数Tab. 1 Performance parameters of the optical system

3.2 设计结果

在优化过程中，由于DMD会使光线偏转24°，因此DMD上的像相对于折转后的光轴是倾斜的，所以需要将像面倾斜设置为变量进行优化[15]。同时，为了避免成像物镜最后一片透镜与反射后的光线发生干涉，需要对成像物镜的后工作距以及投影物镜的前工作距进行控制[16]。最终光学系统的结构图如图5所示，光学系统的传递函数图6（彩图见期刊电子版）所示。可以看出，光学系统成像质量良好，在探测器截止频率处的传递函数接近衍射极限。

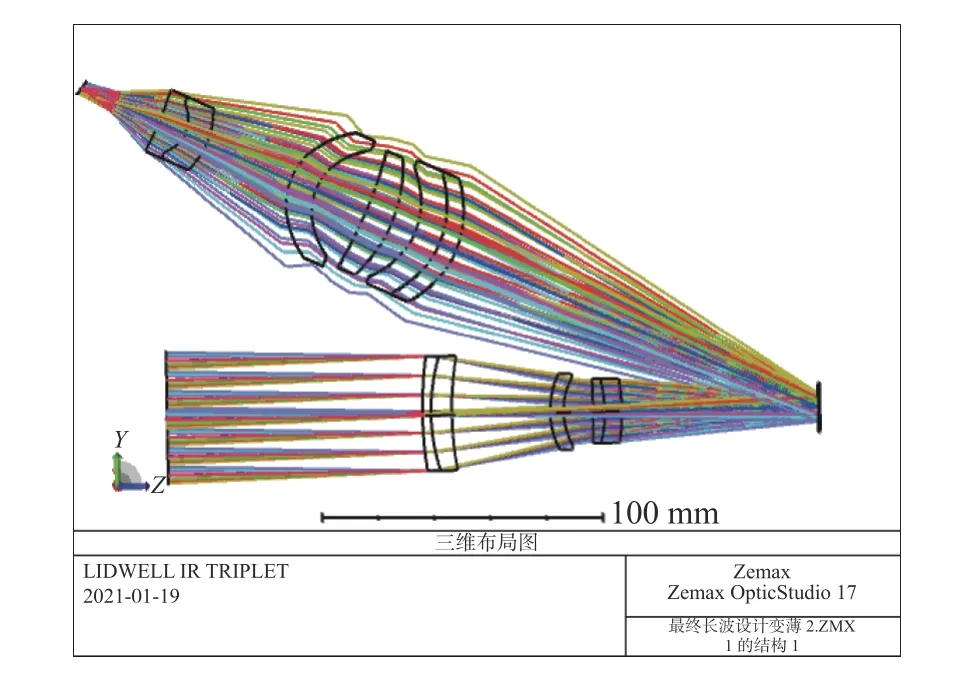
图 5 光学系统结构图Fig. 5 Structural diagram of optical system

图 6 光学系统的传递函数Fig. 6 Transfer function of the optical system

4 仿真分析系统装调误差对超分辨重建结果的影响

根据上述DMD超分辨成像光学系统的成像模型，在所设计的超分辨成像光学系统中分别引入偏心、倾斜、镜片间隔误差、离焦等装调误差，从Zemax软件中可以得到引入装调误差后，具有不同视场的光学系统的PSF，再使用上述针对空间变化的PSF获取方法获取PSF，并将获取的PSF代入上述仿真模型中进行分析。

本文所设计的超分辨成像光学系统在X和Y方向的视场并不相同，在光学系统中引入装调误差时需要对每片透镜的X、Y方向分别引入适量的误差进行分析。

公差分析方法主要有3种：灵敏度分析、反转灵敏度分析和蒙特卡罗分析[17]。灵敏度分析是指对于给定的一组公差变量，计算出各评价标准的变化；反转灵敏度分析是指根据每个公差在性能方面给定的最小允许减小量来计算公差；蒙特卡罗分析是利用某种统计方法，一般有均匀分布、正态分布和抛物线分布等，产生一系列的满足制定公差的随机镜头，然后再按标准进行评估[18]。本文采用反转灵敏度分析法，以重建图像的PSNR值下降1为基础，对系统进行公差分析。

4.1 镜片偏心对超分辨重建结果的影响

对光学系统的每片透镜的X、Y方向分别引入适当偏心误差，每次引入0.01 mm的偏心量，将引入误差后的PSF代入成像模型进行图像重构。图7（彩图见期刊电子版）为每片镜片偏心量与重建图像PSNR值之间的关系。

图 7 镜片偏心量与重建图像PSNR值的关系Fig. 7 Relationship between lens eccentricity and PSNR value of reconstructed image

由图7可知，第7片镜片的偏心误差对重建结果影响最大，当第7片镜片X方向引入0.11 mm的偏心误差或Y方向引入0.07 mm的偏心误差时，重建图像PSNR值下降1。

4.2 镜片倾斜对超分辨重建结果的影响

对光学系统的每片透镜的X、Y方向分别引入倾斜误差，再使用上述成像模型对图像进行重构，每次引入0.01°的倾斜量。图8（彩图见期刊电子版）为每片镜片的倾斜量与重建图像PSNR值之间的关系。

图 8 镜片倾斜量与重建图像PSNR值的关系Fig. 8 Relationship between lens tilt and PSNR of reconstructed images

由图8可知，当第6片透镜X方向倾斜0.10°或第6片透镜Y方向倾斜0.14°时重建图像PSNR值下降1。

4.3 镜片间隔误差对超分辨重建结果的影响

改变每两片透镜之间的距离，每次改变0.01 mm，再使用上述成像模型对图像进行重构。图9（彩图见期刊电子版）为镜片间隔误差与重建图像PSNR值之间的关系。

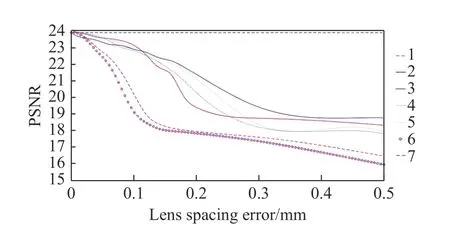
图 9 镜片间隔误差与重建图像PSNR值的关系Fig. 9 Relationship between lens spacing error and the PSNR of reconstructed images

由于光学系统的物面在无穷远处，第1片镜片与物面的间隔误差对重建结果没有影响，第6片镜片的间隔误差对图像重建结果影响最大，当第6片镜片间隔误差为0.04 mm时，重建图像PSNR值下降1。

4.4 光学系统离焦对超分辨重建结果的影响

分别改变成像物镜和投影物镜与像面之间的距离，每次引入0.01 mm的离焦量，再使用上述成像模型对图像进行重构。图10为光学系统离焦量与重建图像PSNR值之间的关系。

图 10 光学系统离焦与重建图像PSNR值之间的关系Fig. 10 Relationship between defocus of the optical system and PSNR value of the reconstructed image

由图10可知，成像物镜和投影物镜的离焦对重建结果影响都比较大，当成像物镜离焦0.06 mm或投影物镜离焦0.10 mm时，重建图像PSNR值下降1。

在上述装调误差分析结果的基础上，再使用蒙特卡罗法对系统进行公差分析，同时在系统中引入上述分析得到的公差范围内的随机量的多种误差组合，再通过成像模型进行图像重建，最终得到重建图像PSNR值下降1时的DMD超分辨成像光学系统的公差范围，表2为100次蒙特卡罗分析得到的多种误差共同作用后的DMD超分辨成像光学系统的公差分配结果。

表 2 公差分配结果Tab. 2 Tolerance allocation results

5 结 论

通过研究装调误差对超分辨成像结果的影响，建立了DMD超分辨成像光学系统的成像模型，并利用该模型对搭建的DMD超分辨成像光学系统获取的数据进行仿真，提出了装调误差对超分辨成像质量影响的分析方法。确定了该超分辨成像光学系统装调时所允许的公差范围，即该系统在加工装调时X方向总体偏心误差控制在±0.07 mm以 内，Y方 向 总 体 偏 心 误 差 控 制在±0.05 mm以内；X方向和Y方向的总体倾斜误差应控制在±0.06°以内；总体镜片间隔误差控制在±0.02 mm以内；成像物镜的离焦量控制在±0.04 mm以 内；投 影 物 镜 的 离 焦 量 控 制 在±0.05 mm以内。