基于数学核心素养的高中数学排列组合解题研究

赵玉娟

摘 要：排列组合问题可以培养学生的数学运算能力和数据分析能力，在高考中主要是以选择、填空的形式出现，分值为5分，应用性强，并且与实际问题相关联，试题具有一定的灵活性和综合性，易于考查学生分析问题的能力。实践证明，关于排列、组合问题备考有效的方法是题型与解法归类，识别模式、熟练运用。

关键词：数学核心素养;高中数学;排列组合

一、绪论

《普通高中数学课程标准（2017年版2020年修订）》（以下简称新课标）指出普通高中的培养目标是进一步提升学生综合素质，着力发展六大核心素养：数学抽象、 逻辑推理、数学建模、直观想象、数学运算和数据分析[1]。排列组合问题可以培养学生的数学运算能力和数据分析能力，高考中主要以选择、填空的形式出现，多与实际问题相联系，并具有一定的灵活性和综合性。实践证明，备考排列、组合问题的有效方法是题型与解法归类，我们要识别模式，熟练运用。

二、归纳分析

排列組合问题考查方式多样，现以下面八种常见的排列组合问题给出方法指导及例题解析。

（一）相邻问题捆绑法

方法指导：对于要求某些元素相邻的问题，需要先将相邻元素看作一个整体，再与其他元素进行排列，同时对相邻元素进行自排。

案例一：7位同学站成一排，甲、乙必须相邻，并且丙不能站在排头与排尾的排法有多少种？

解析1：首先甲乙必须相邻，采用捆绑法，将二者看作一个整体A22，此时相当于有6个元素，丙不能站在排头和排尾，从除丙之外的5个元素中选出两个站在排头排尾A25，剩下4个元素全排列A44，A22×A25×A44=960。

解析2：甲乙捆绑A22，此时相当于有6个元素，从丙可以选择的位置入手，从中间4个位置选一个给丙A14，剩下5个元素全排A55，A22×A14×A55=960。

解析3：排除法A22。甲乙捆绑，6个元素进行全排列A66，减去丙在排头和排尾的情况，丙在排头和丙在排尾各有A55种排法，A22（A66-2A55）=960。

（二）不相邻问题插空法

方法指导：对于不相邻问题用插空法，先排除没有要求的元素，让不相邻的元素插空。

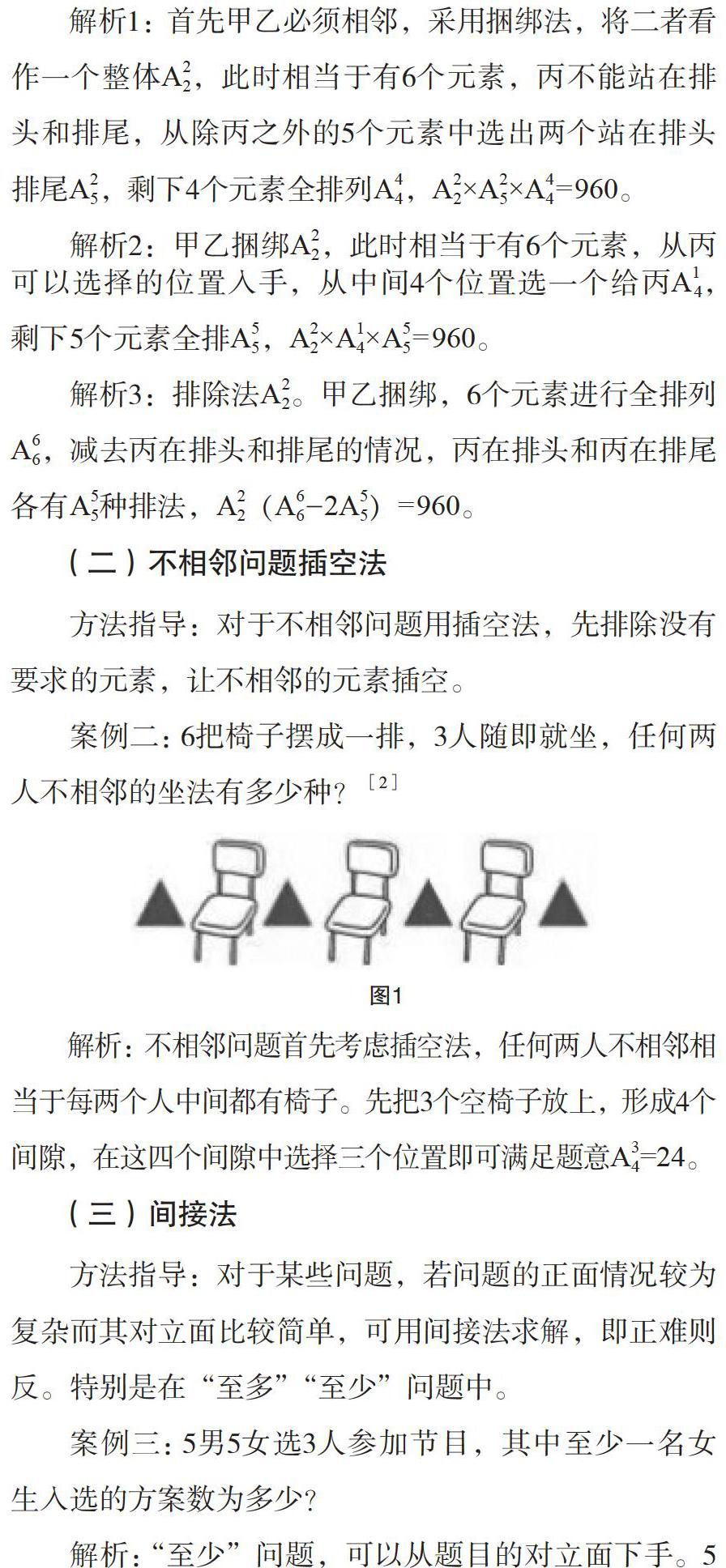
案例二：6把椅子摆成一排，3人随即就坐，任何两人不相邻的坐法有多少种？[2]

解析：不相邻问题首先考虑插空法，任何两人不相邻相当于每两个人中间都有椅子。先把3个空椅子放上，形成4个间隙，在这四个间隙中选择三个位置即可满足题意A34=24。

（三）间接法

方法指导：对于某些问题，若问题的正面情况较为复杂而其对立面比较简单，可用间接法求解，即正难则反。特别是在“至多”“至少”问题中。

案例三：5男5女选3人参加节目，其中至少一名女生入选的方案数为多少？

解析：“至少”问题，可以从题目的对立面下手。5男5女共10人，选3人C310，减去没有女生入选的方案，相当于只从男生中挑选5人C35，C310-C35=110。

（四）隔板法

方法指导：用来解决相同元素之间的分配问题[3]。

案例四：求方程x1+x2+x3+x4=10的正整数的解的组数。

解析：将10个完全相同的球排成一列，会形成9个间隙，在这9个间隙中任意选择3个空，就能将10个球分成4份，每一份球的个数为x1、x2、x3、x4，此时x1+x2+x3+x4=10。同理，方程的解的组数与插入隔板的方法对应，即C39=84。

（五）分组问题

方法指导：一般地，n个不同元素分成p组，各组元素数目分别为m1，m2 …，mp。其中k组元素数目相等，那么分组方法数是。

案例五：有2个红球、3个黄球、4个白球。同色球不加以区分，将这九个球排成一列有多少种排法？

解析：同色球不加以区分等价于相同颜色的球不考虑顺序。先将9个球全排A99，再除以红球、黄球、白球的顺序A99，A99/A22×A33×A44=1260。

（六）特殊元素（位置）——先选后排

方法指导：某些元素（位置）的排法受到限制，解题时，应先考虑这些元素，这种方法叫作元素分析法，也可以优先考虑位置，这种方法叫作位置分析法。

案例六：3男4女按照不同要求排队，全体站成一排，其中甲不在最左端，且乙不在最右端，有多少种方案？

解析：元素分析法，如果甲在最右端，剩下的6个元素没有限制，进行全排A66;如果甲不在最右端，并且甲也不能在最左端，剩下5个位置可以选择。甲选完之后，乙选择，减去甲和最右边的位置，乙有5个位置可以选择，剩下5个人进行全排A55。A66+5×5×A55=3720。

（七）定序问题缩倍法

方法指导：对于某些元素的顺序已经确定的问题称为定序问题，常用除法处理，先不考虑顺序限制，排列后，再除以定序元素的全排列个数。

案例七：5男5女排成一排，女生从高到矮的顺序排列，共有多少种排法？

解析： 有10个位置，先将男生排在其中任意5个位置A310，在男生排完之后，将女生安排在剩下的5个空，而剩下的5个女生只有1种排法，所以排法种数为A310×1=30240。

（八）多元问题分类法

方法指导：元素多，取出的情况也多种，可以按照结果要求分成不相容的几类情况分别计数，最后总计。

案例八：从1，2，3，…，100中任取2个数，使它们的乘积能被7整除，这两个数的取法（不计顺序）共有多少种？

解析：被取的两个数中至少有一个能被7整除时，它们的乘积就被7整除，将这100个数分为两组，能被7整除的数的集合记作A={7，14，21，…，98}共14个元素，不能被7整除的数的集合记作B={1，2，3，…，100}，共86个元素。当两个数都从A中取时C214=91，当其中一个数从集合A中取，另一个数从集合B中取时，C114C186=1204，共有C214+C114C186=1295。

三、结语

本文总结了八种方法，基本包含了高中数学排列组合题目所有的应用情况和应用策略，能够解决实际问题，从而引导学生更好地理解和掌握这部分知识，提高学生的解题水平，培养高中数学核心素养中的数学运算能力和数据分析能力，为高考奠定坚实的基础[4]。在排列组合教学过程中要引导学生思考，总结题目考查的是哪个知识点，会与哪些知识相关联，是以什么形式来出题的，题目中隐藏的信息有哪些，怎样将已有知识综合运用到题目中，多角度分析问题的来龙去脉，从而掌握解决每类问题的通法。

参考文献

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2]薛金星.怎样解题[M].北京：北京教育出版社，2017.

[3]于水青.排列组合问题的求解方法与技巧[J].山西师范大学学报（自然科学版），2014，28（S2）：15-17.

[4]伍春兰.检视高考数学第一轮复习——以排列组合复习为例[J].数学通报，2017，56（12）：37-38.