考虑温度和加载影响的离子型中间膜拉伸力学性能

陈素文，陆钰佳，邵 筱

（1.同济大学土木工程防灾国家重点实验室，上海200092；2.同济大学土木工程学院，上海200092）

夹层玻璃是一种通过高温高压处理将多层玻璃面板和中间层材料结合在一起的复合面板。中间层材料的剪切模量决定了玻璃面板之间剪力传递的效率，而其拉伸性能直接影响了玻璃面板破碎后夹层玻璃的残余承载力［1］。离子型中间膜，作为一种基于乙烯和甲基丙烯酸离聚物［2-3］的新型高性能的中间层材料，与传统中间层材料PVB（polyvinyl butyral）相比，具有强度高、模量大、延性好且温度敏感性低的优点［2，4-6］。Kuraray公司的SentryGlas®（简称SG）是目前市场上唯一可用于外玻璃幕墙的离子型中间膜［7］，已经被大量应用于实践工程中。然而，对其不同荷载作用下的力学性能仍缺乏全面系统的研究。已有研究多关注离子型中间膜的单调拉伸性能，且主要集中于单调拉伸行为的应变率效应［4，8-9-13］：Bennison等［4］在0.1 s-1～125 s-1下进行了单调拉伸试验，发现随着应变率的增加，离子型中间膜的屈服应力提高而极限应变减小，初始模量与应变率没有显著关系，Belis等［8］也得到了类似的结论。Zhang等［9］在0.0056 s-1～2000 s-1下进行了单轴拉伸试验，结果表明离子型中间膜的初始模量表现出显著的应变率效应，这与Bennison等［4］和Belis等［8］的结论相反。张洋［10-12］的试验结论与Zhang等［9］相同，并认为模拟夹层玻璃破碎后力学行为时，有必要考虑中间层材料应变率效应，给出了中高应变率下离子型中间膜的本构模型。此外，因为离子型中间膜是一种半晶态聚合物，所以温度的影响不可忽略［14］。动态力学试验结果［5，15］表明，SG的剪切模量确实随温度的升高而减小。Delincé等［16］认为，当温度低于55°C，SG表现为弹粘塑性材料，而温度高于55°C时，SG表现为超弹性材料。而张洋［10］与Santarsiero等［17］的研究表明，当温度从20℃升高至40℃，初始弹性模量的降低幅度最大，即在该温度范围内，材料的性能有显著变化。综上，国内外温度效应下离子型中间膜的材料力学性能数据相对有限，温度效应对该材料拉伸性能的影响还需进一步的研究。此外，对于荷载作用后玻璃面板发生自由振荡进而回弹的夹层玻璃，应考虑加卸载过程对于离子型中间膜拉伸性能的影响［18］，但尚未见相关研究报道。

为此，本文开展了离子型中间膜的单调和循环加卸载拉伸力学性能研究，对离子型中间膜进行了-40°C～80°C和0.001 s-1～0.1 s-1下的单调拉伸试验，以及室温和0.001 s-1～0.1 s-1下的循环加卸载拉伸试验，得到了应力-应变曲线以及弹性模量、抗拉强度、塑性应变、耗能能力等力学性能特征指标，分析了应变率和温度的耦合效应对其单调拉伸性能、以及应变率对其循环加卸载拉伸性能的影响，进一步建立了描述其单调和加卸载拉伸力学性能的模型。研究成果为离子型中间膜在夹层玻璃的应用研究提供支撑。

1 试验概况

1.1 单调拉伸试验

单调拉伸试验所用离子型中间膜为SG（SentryGlas®），单调拉伸试件均切割于同一片名义厚度为1.52 mm的膜材。试件几何尺寸均按照GB/T528-2009［19］中的3型试件设计，见图1。

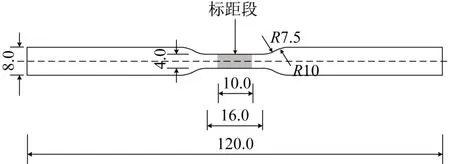
图1 单调拉伸试验和循环加卸载试验试件尺寸（单位：mm）Fig.1 Dimensions of specimens for monotonic and cyclic loading-unloading tests(unit:mm)

单调拉伸试验在岛津Shimadzu AG-250 kN电子万能试验机上完成，过程中采用试验机匹配的温度箱控制加载环境温度，采用视频引伸计记录加载过程中试件的变形，见图2。

图2 单调拉伸试验的试验装置Fig.2 Test setup for monotonic tensile tests

试验加载采用位移控制，由预设应变率和试件标距段的长度确定加载速率。单调拉伸试验在不同温度和应变率下进行，预设-40°C、-20°C、0°C、20°C、40°C、50°C、55°C、60°C、70°C、80°C共10种温度状态，以及0.001 s-1、0.01 s-1和0.1 s-1共3种应变率状态，一共30个工况。每个工况进行3次重复试验，共90个试件。对单调拉伸试件进行编号，以20°C-B-2为例，20°C和B分别代表该工况的温度和应变率，A、B、C分别代表3种应变率0.1 s-1、0.01 s-1、0.001 s-1，2表示该工况的第2个试件。当温度低于55°C时，采用试验机配套夹具直接夹持，见图3a。当温度高于55°C时材料较软不易夹持，将试件端部加工成空心柱状，然后用连接杆和转接夹具将试件固定在试验机上，见图3b。

图3 单调拉伸试验的夹具Fig.3 Grips for monotonic tensile tests

1.2 循环加卸载拉伸试验

循环加卸载拉伸试件切割于同一片名义厚度为0.76 mm的SG膜材。试件几何尺寸见图1。循环加卸载拉伸试验在ETM电子万能试验机上完成，试验环境温度为25°C±5°C。试件标距段的变形由数字图像相关技术DIC（Digital Image Correlation）测量，试验前在试件平行段上粘贴标记点以标记标距段，见图4。

图4 循环加卸载试件的标记点Fig.4 Marks on specimen of cyclic loadingunloading tensile tests

循环加卸载拉伸试验的加载制度如图5和表1所示，预设0.001 s-1，0.005 s-1、0.01 s-1、0.05 s-1和0.1 s-1共5种应变率。0.001 s-1下，取3个试件进行单调拉伸试验，后4种应变率下，各取3个试件进行单调拉伸试验和循环加卸载试验，共27个试件。对试件进行编号，以M/C-0.1s-1-2为例，M和C分别表示单调拉伸和循环加卸载拉伸工况，0.1 s-1代表该工况的应变率，2表示相应工况的第2个试件。

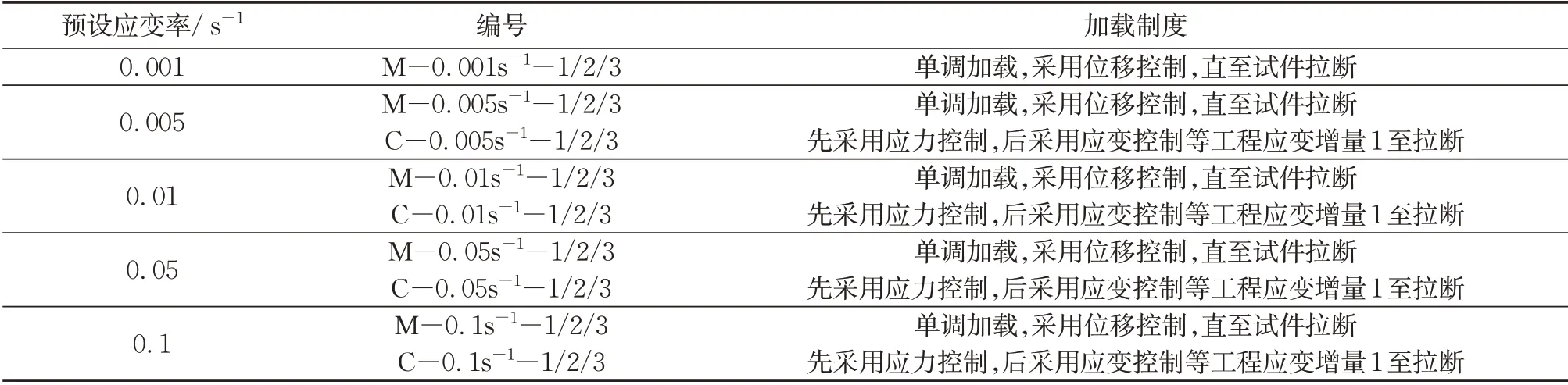
表1 循环加卸载试验工况设置Tab.1 Loading programs of cyclic loading-unloading tensile tests

图5 循环加卸载试验的加载制度Fig.5 Loading schemes for cyclic loading-unloading tensile tests

2 试验结果及分析

2.1 单调拉伸性能

单调拉伸试验初期，试件即出现明显的轴向拉伸变形和横向截面收缩，直至试件拉断试件也未出现明显的颈缩现象，如图6。所有单调拉伸试件的断口形状特征基本一致，大部分试件的断裂位置在试件标距段内，见图7，认为破坏在标距段端部试件的试验数据无效并重复试验。

图6 加载过程中试件20°C-0.01s-1-1的变形过程Fig.6 Deformation process of 20°C-0.01s-1-1

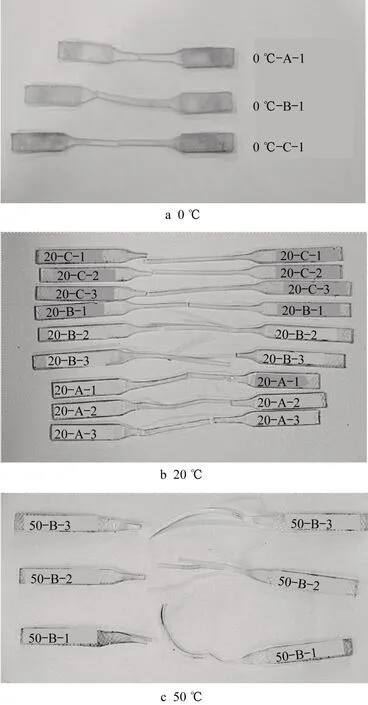
图7 单调拉伸试验断裂后试件Fig.7 Fractured specimens of monotonic tensile tests

试验中材料的工程应力σeng由力传感器所记录荷载F，以及试件初始截面面积A0确定

工程应变εeng由视频引伸计记录的标距段的长度L以及初始长度L0确定

考虑离子型中间膜在试验中发生了大变形，工程应力、工程应变不足以描述材料的真实力学性能，因而将工程应力、工程应变转化为真实应力σtrue和真实应变εtrue

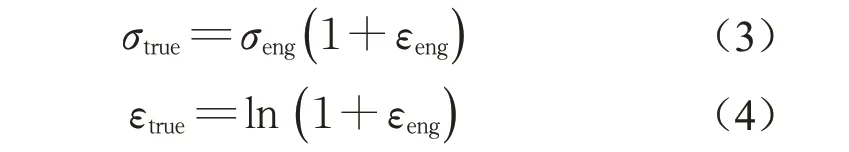
图8为不同温度、3种应变率下单调拉伸试验的真实应力-应变试验曲线。可以看出，20°C以下，加载初期，各工况下的试验曲线均呈现基本线性关系，而后进入屈服及后继强化阶段，曲线表现出弹塑性特征。在-20°C～20°C，试件在屈服后还会进入应变软化阶段。当温度达40°C及以上时，真实应力-应变曲线初始弹性阶段急剧变平缓，40°C左右，离子型中间膜的后继强化现象更加显著，曲线表现出类似超弹性特征。各应变率下，随温度升高，相同应变水平的应力均明显降低，当温度从20°C升至40°C时，相同应变下的应力降低幅度最大。同时材料的极限应变也随温度升高而明显增大，表明材料延性随温度升高而得到改善。

为进一步分析温度和应变率耦合效应对离子型中间膜单调拉伸性能的影响，根据试验曲线确定了相关力学指标，包括初始弹性模量，名义屈服强度和名义屈服应变，以及抗拉强度和相对应的极限应变，见图9a～图9c。其中初始弹性模量取应变范围为0～0.1%的割线模量，名义屈服强度取残余应变为0.2%时的应力值，屈服应变为对应的应变值。

图9 力学参数随温度和应变率变化的对比Fig.9 Comparison of mechanical parameters with temperature and strain rate

可以看出，温度对离子型中间膜力学性能的影响十分显著。初始弹性模量随温度的升高而降低，20°C～40°C的降低幅度最为显著，20°C时初始弹性模量仅为-40°C时的50%，40°C时，初始弹性模量减小为-40°C时的10%～30%。从整体上看，随温度的升高，材料的屈服强度呈减小趋势，而屈服应变的基本稳定。极限应变随温度升高而明显增大，这表明离子型中间膜在高温下材料延性更好。但抗拉强度随温度的变化规律不明显，这可能是不同温度下极限应变的差距导致的。实际上，在相同的应变水平下，应力会随温度的提高而减小，如图8所示。

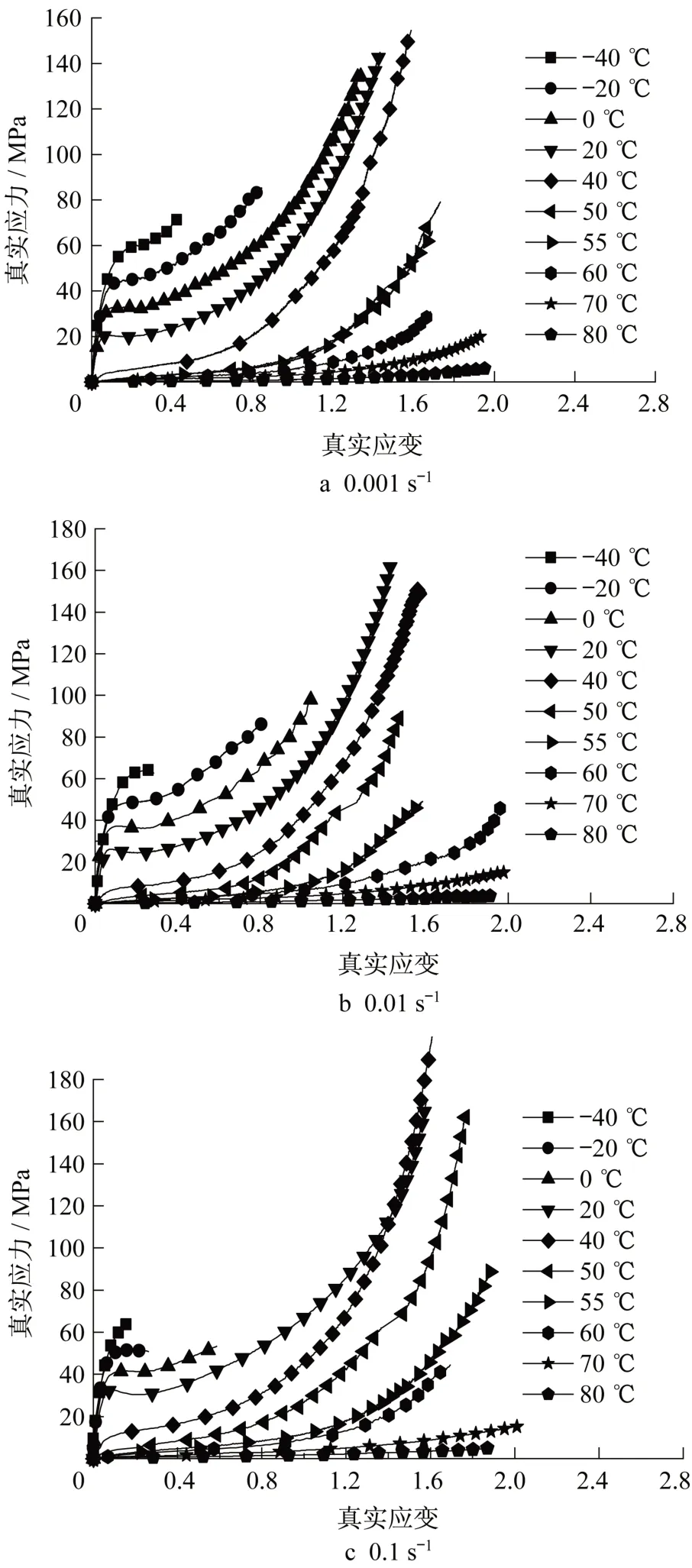
图8 单调拉伸试验真实应力-应变曲线Fig.8 True strain-stress curves of monotonic tensile tests

结果也表明，应变率对该材料单调性能的影响与温度相反，即随应变率的提高，初始弹性模量、屈服强度以及相同应变水平的应力增大而极限应变减小。

2.2 循环加卸载拉伸性能

循环加卸载试验中，所有试件均在标距段内破坏，断裂后的试件总长度大于试验前的试件长度。10-3s-1下，单调加载破坏后试件的残余变形随时间的变化如图10所示。由于材料的粘性，试件的变形在断裂后一周之内有小部分恢复，但一周之后变形基本稳定不再减少。这表明离子型中间膜在荷载作用后产生的变形大部分为稳定不会恢复的塑性变形。

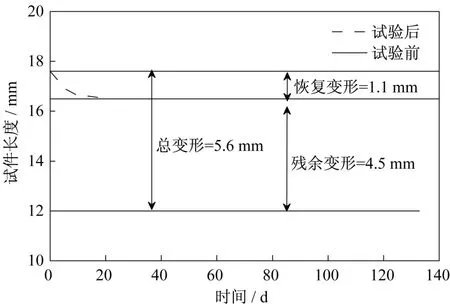
图10 M-0.001s-1-1试件变形随时间变化Fig.10 Deformation of M-0.001s-1-1 vs.time

图11为循环加卸载拉伸试验的真实-应力应变曲线。加卸载曲线的包络线与单调曲线基本一致，表明在单调和循环加卸载拉伸荷载下材料性能没有明显差异。从整体上来看，所有应变率下的循环加卸载曲线均出现了明显的滞回环。卸载应变较小时，卸载段表现为先线性后明显的非线性，随着卸载应变的增大，卸载段的非线性明显减弱，这可能是由离子型中间膜进入后继强化阶段，材料粘性的减弱导致的。再加载段的非线性发展和卸载段类似，即随卸载应变增大，非线性现象减弱。因而，随卸载应变的增大，加卸载曲线滞回环的饱满程度也明显下降。

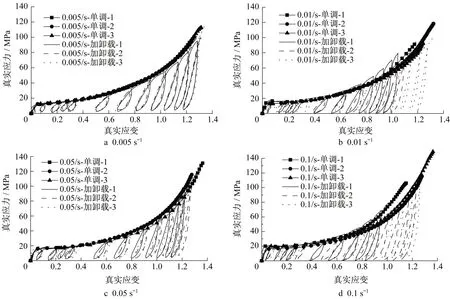
图11 循环加卸载试验真实应力-应变曲线Fig.11 True strain-stress curves of cyclic loading-unloading tensile tests

夹层玻璃面板受到破坏荷载作用时，中间层是潜在的耗能材料，其在循环荷载下的塑性变形是评价其材料性能的重要指标，在此定义塑性应变为再加载点的应变，见图12。

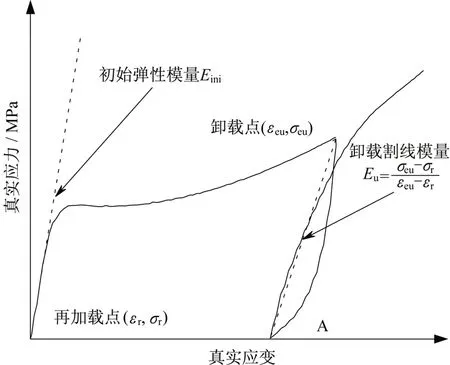
图12 塑性应变和割线卸载模量的定义Fig.12 Definition of plastic strain and unloading se⁃cant modulus

图13给出不同应变率下，离子型中间膜的塑性应变随卸载应变的变化情况，整体来看，离子型中间膜的塑性变形能力较强。塑性应变与卸载应变基本呈正相关关系，拟合斜率约为0.93。这表明，在加载过程中，塑性应变随卸载应变的增大而增大，且塑性应变的累积速率较小于卸载应变的增加速率。图13也表明，应变率对塑性应变发展的影响不大。

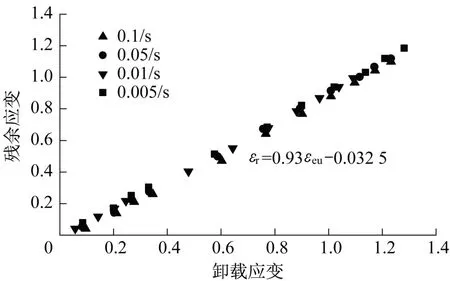
图13 各应变率下卸载应变与塑性应变关系Fig.13 Plastic strains at different unloading strains and strain rates

滞回圈的能量耗散面积可用于进一步分析和评价离子型中间膜的耗能能力。不同应变率和卸载应变水平下，该材料的能量耗散面积计算结果如图14所示。从整体来看，离子型中间膜的耗能能力较强，且随卸载应变水平的增大而提高。应变率对耗能能力的影响如下：当卸载应变低于0.4时，即离子型中间膜进入后继强化阶段前，其耗能能力随应变率增大而减小，这可能是由应变率增大导致材料黏性减弱导致的；而当卸载应变高于0.4时，应变率对耗能能力的影响规律还不明显，所以对于爆炸荷载涉及的中高应变率情况，其耗能随应变率的发展情况还需要进一步通过试验来确定。

图14 各应变率下不同卸载应变水平的耗能Fig.14 Energy dissipation at different unloading strains and strain rates

为考察加卸载过程中离子型中间膜的模量变化，在此定义割线卸载模量Eu，如图12，即卸载点和再加载点连线的斜率。图15为0.1s-1下不同卸载应变水平的割线卸载模量的对比。可以看出，割线卸载模量随卸载应变的增大先减小后增大：在离子型中间膜进入后继强化阶段之前卸载时，割线卸载模量随卸载应变的增加而减小，而进入后继强化之后再卸载时，割线卸载模量会随卸载应变的增加而增大，甚至在最后一级卸载时，割线卸载模量远大于初始弹性模量。

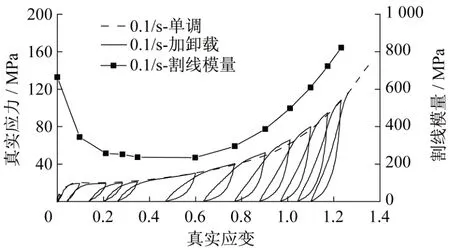
图15 0.1s-1下不同卸载应变下割线卸载模量的对比Fig.15 Comparison of unloading secant modulus at different unloading strain

段芳莉等［20］指出，从半晶态聚合物拉伸变形的微观机理来看，后继强化之前主要发生非晶区的拉伸及解缠结、晶区的滑移，而材料进入后继强化之后，前述运动基本完成，主要发生的是分子链的重新取向。可以从该微结构运动角度解释卸载割线模量随卸载应变增大先减小后增大的变化现象：在离子型中间膜进入后继强化前，主要表现一种粘塑性材料，割线卸载模量的减小可能是由其内部结构中的力学损伤导致的，如分子链的断裂和晶体区的滑移；而离子型中间膜进入后继强化之后，晶体部分的滑移已经达到最大，非晶体部分的拉伸也基本完成，即力学损失已经达到最大，此时分子构象熵的进一步演化会导致割线卸载模量的增大。

为表征离子型中间膜的模量变化，定义模量比

式中，Einitial和Eu分别表示初始弹性模量和割线卸载模量，如图12所示。图16给出各应变率下模量比随卸载应变的变化，各应变率下该值均随卸载应变的增大先减小后增大。在较高应变率如0.1s-1下，后继强化前割线卸载模量的减小幅度更明显，而后继强化后的增大幅度均小于其他应变率下的增大幅度。但从整体上看，应变率对割线卸载模量的影响规律尚不明显。

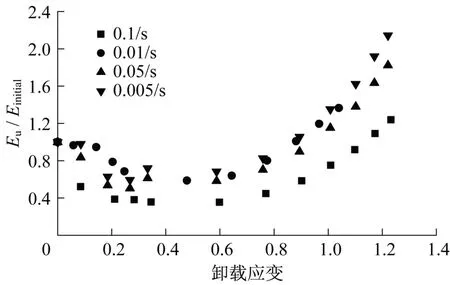
图16 各应变率下割线卸载模量的对比Fig.16 Comparison of unloading secant modulus at different stain rates

3 材料模型

3.1 本构模型

G’Sell模型是适用于固相聚合物的经验型动态本构关系［21］，该模型基于对固相聚合物试验数据的分析，将其力学响应归结为粘弹性和塑性共同作用的结果，且这两个因素是相互独立的。此外，该模型假设材料的粘弹性仅受应变影响，而材料的塑性发展是应变和应变率的共同作用的结果。本构关系为

式中，比例因子K、黏性参数ϖ、应变强化系数h、应变率系数m和温度系数a，共5个模型参数。基于本文单调拉伸试验结果，标定模型参数列于表2。

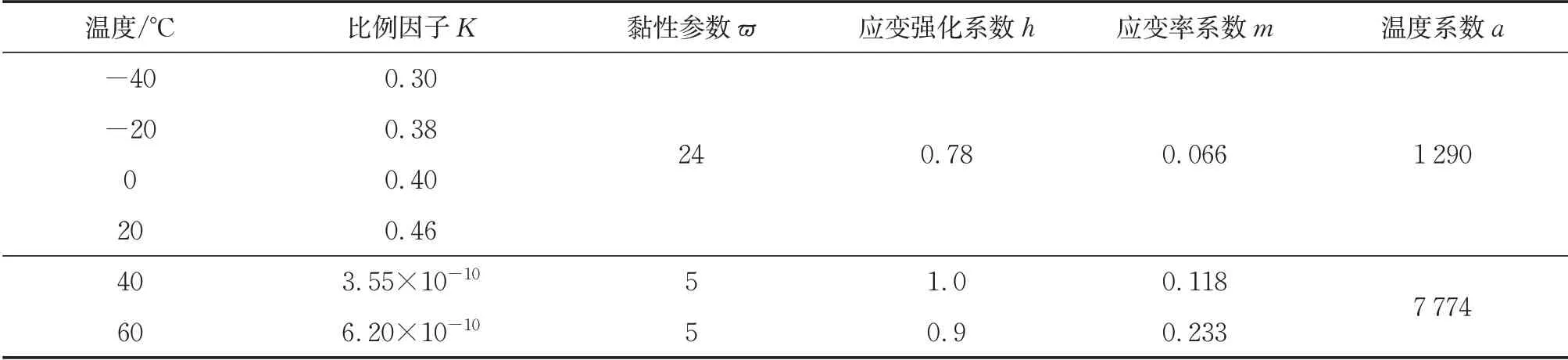
表2 G’Sell本构模型参数Tab.2 Parameters of G’Sell constitutive model

图17给出了本文及已有研究［5，8，17］中单调拉伸试验中的真实应力-真实应变曲线和上述模型预测的曲线的对比图，可以发现二者吻合良好。

图17 模型预测结果与试验结果的比较Fig.17 Comparison between published results and model predictions

3.2 变模量模型

由2.2节对于加卸载拉伸试验数据的分析可知，循环加卸载下该材料割线卸载模量随卸载应变的变化，是力学损失的累积和构象熵的演化两种机制共同作用的结果。所以综合考虑这两种机制的作用，离子型中间膜卸载割线模量比D的变化可定义为

式中，Ddamage表示加载过程中，分子链的断裂和晶体区的滑移对材料造成的力学损伤。随着力学损伤的累积，卸载割线模量减小。Nnetwork为分子网络构象熵演化对卸载割线模量的影响，即分子构象熵的进一步演化导致割线卸载模量的增大。

采用Yoshida等［22］提出的弦线模量模型描述力学损失Ddamage随卸载应变εeu的变化

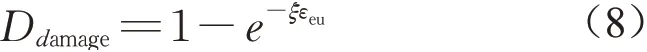
式中ξ为材料参数，εeu为卸载应变，由试验数据标定。采用以下数学模型描述Nnetwork随卸载应变εeu的变化

式中，α是材料参数，由试验数据标定。基于本文循环加卸载拉伸试验数据，标定模型参数列于表3。

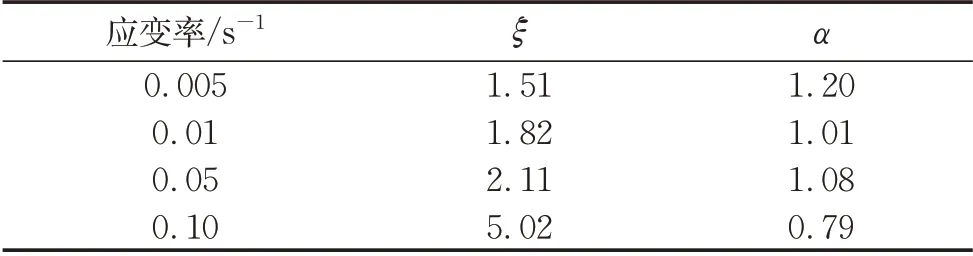
表3 变模量模型材料参数Tab.3 Parameters for variable modulus model

循环加卸载试验结果表明，加卸载曲线包络线与单调拉伸曲线一致，所以包络线部分可采用G’Sell本构模型描述。图18对比了0.05 s-1和0.1 s-1下变模量模型预测的曲线与本文试验曲线。对比结果表明，所提出变模量模型可以较准确描述循环加卸载下离子型中间膜真实应力应变的发展，但是尚不能描述应变滞后现象导致的耗能行为。

图18 变模量加卸载模型与试验曲线对比Fig.18 Comparison predicted results and test results

4 结论

（1）20°C以下和40°C以上（含40°C），离子型中间膜的单调拉伸曲线分别表现出粘弹塑性和类超弹性特征。

（2）初始弹性模量随温度的升高而降低，20°C～40°C的降低幅度最为显著，20°C时初始弹性模量仅为-40°C时的50%，40°C时，初始弹性模量减小为-40°C时的10%～30%。随温度升高，该材料的抗拉强度降低，而极限应变提高。

（3）低应变率下，应变率对单调拉伸力学性能的影响与温度相反。

（4）荷载作用下，离子型中间膜的变形大部分为不可恢复的塑性变形，小部分变形在荷载作用结束后可以恢复。

（5）循环加卸载拉伸曲线的包络线与其相同条件下的单调拉伸试验曲线基本一致。

（6）循环加卸载耗能能力随卸载应变的增大而提高，割线卸载模量随卸载应变先减小后增大。

（7）基于试验结果，给出了低应变率范围内不同温度下离子型中间膜的本构关系；在此基础上，引入割线卸载模量，提出描述该材料在循环加卸载下拉伸力学性能的变模量模型。

作者贡献说明：

陈素文：指导研究开展、文章撰写及修改；

陆钰佳：参与试验研究、理论分析及文章初稿撰写；

邵筱：参与试验研究及理论分析。