基于加权特征投影的信源数估计方法
王 纯,高于晰
(西安建筑科技大学 信息与控制工程学院,西安 710055)
0 引言
波达方向(DOA,direction of arrival)估计作为阵列信号处理的重要研究方向在雷达、通信、声呐和生物医学等众多领域有至关重要的地位[1]。而绝大多数基于子空间类的算法需要已知信号源的数目,若信源数目出现欠估计或过估计,将直接影响DOA估计的结果[2-3]。故准确的信源数估计是DOA估计的先决条件。并且在实际应用中,由于系统对实时性的要求和阵列各阵元间的相关性,导致采样数有限和色噪声的干扰,传统针对白噪声的信源数估计方法在该背景下往往失效,因此研究色噪声/低快拍下的信源数估计方法具有十分重要的意义。
常见的信源数估计方法包括特征值分解法、信息论方法[4-7]、盖氏圆方法(GDE,gerschgorin’s disks estimation)[8-10]和正则相关技术[11]、使用深度学习的方法[12]。特征值分解法是通过信号特征值与噪声特征值的大小差异,并结合阶跃准则实现信源数估计,计算简单且准确度较高,但不适用于低快拍、低信噪比和色噪声条件。采用深度学习[12]的信源数估计方法能够在特定条件下取得很好的效果,然而当环境变化就需要重新对网络进行训练,因此实用性有限。基于信息论的信源个数估计方法[7]包括Akaike信息论准则(AIC,akaike information theoretic criter)、最小描述长度准则(MDL,minimum description length criterion)等计算量小,能很好地应用于白噪声条件,但在色噪声条件下往往失效。近年来,学者对色噪声背景下的信源数估计进行了相关研究。文献[13]将对角加载技术用于信息论信源数估计方法,较好地改善了算法在色噪声条件下的估计性能,而加载量的不同在一定程度上会对算法稳定性产生影响。正则相关技术[11]也可用于色噪声条件,但需要两个空间分离的阵列,大大降低了阵列的有效孔径,实际工程使用性不强。文献[14]利用对数函数对特征值进行拟合,改善了特征值的发散程度,而拟合函数参数的固定在一定程度上降低了算法的鲁棒性。盖氏圆信源数估计方法没有限定噪声模型,因此可以应用于白噪声与色噪声环境,但是在低快拍和低信噪比条件下成功估计概率降低,且该算法在酉变换过程中牺牲了一个自由度,使得计算过程产生的特征向量无法使用于后续的DOA估计。文献[15]在盖氏圆方法的基础上进行了升维处理,节省了一个自由度,但要对盖氏圆半径经过M-1次拟合计算量较大,且在低快拍条件下性能有所下降。
在此基础上,本文通过对数据协方差矩阵在色噪声/低快拍条件下的分析,提出了一种基于加权特征投影的信源数估计方法。该方法在降噪数据协方差矩阵特征值的基础上引入信号子空间与噪声子空间的正交性,构建了加权空间矩阵,并将降噪后的协方差矩阵在该空间上进行投影,利用投影得到的结果构建判决函数,进而实现信源数估计。
1 信号模型
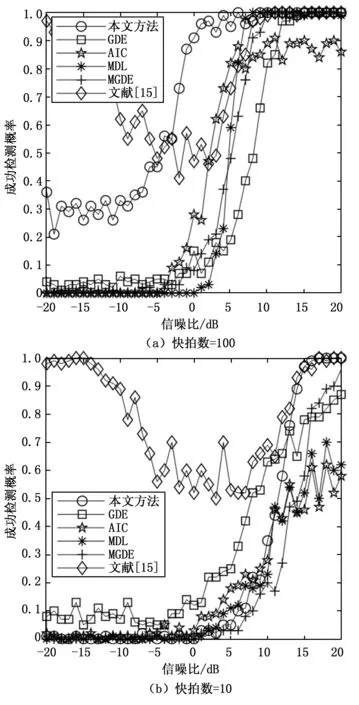
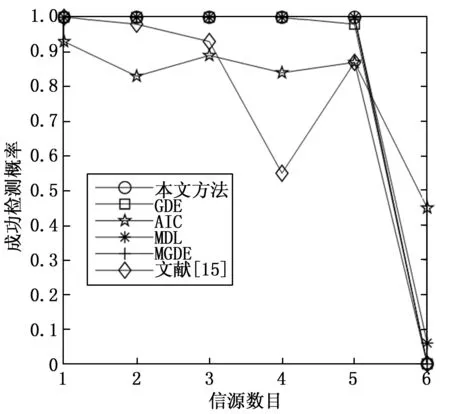
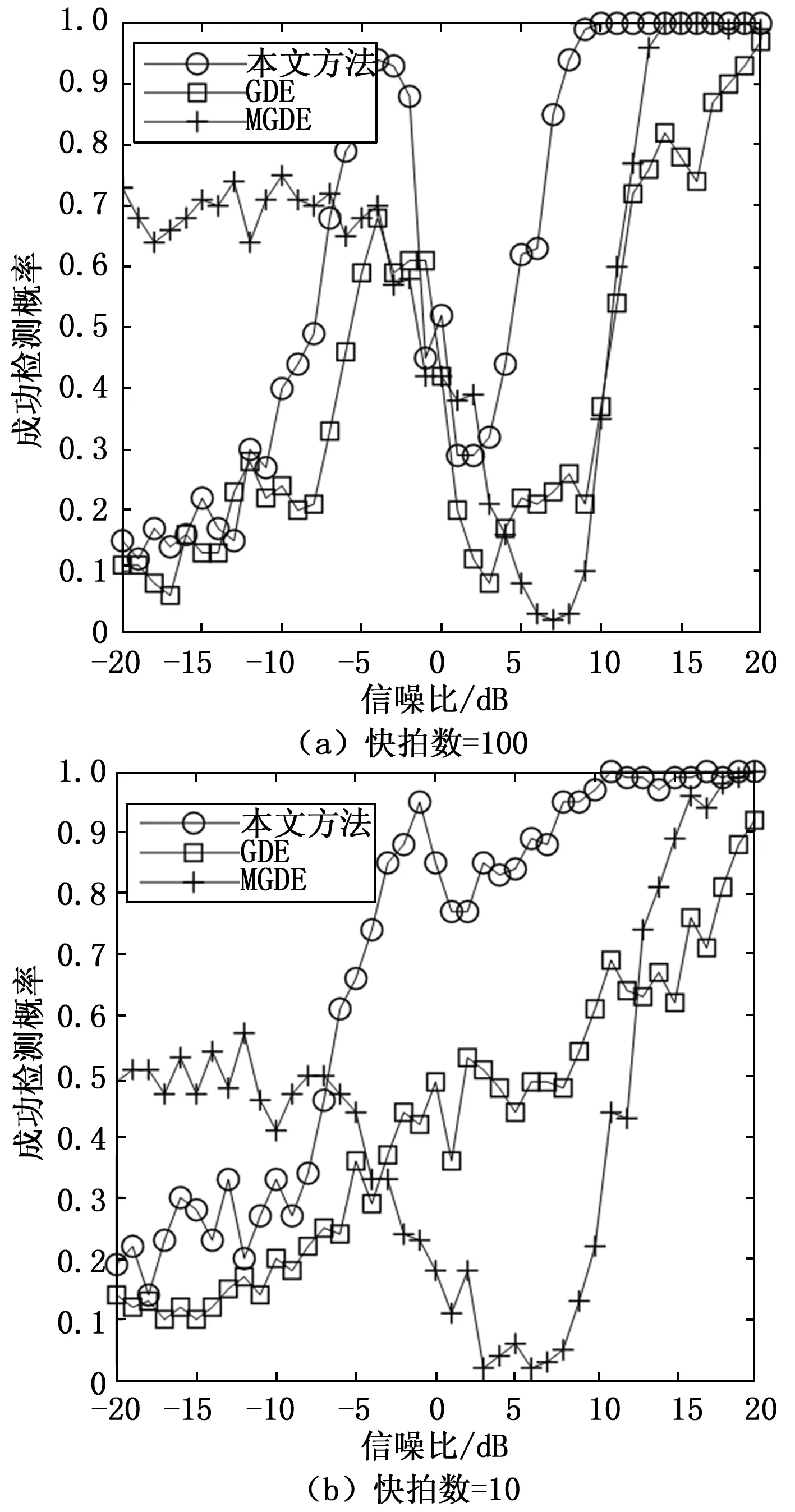
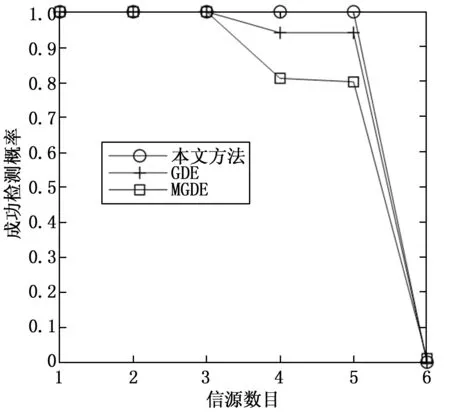
假设一M元均匀放置的天线阵列,阵元间距为半波长,有K个远场窄带不相干的信号从(θ1,θ2,θ3,…,θK)入射到阵列(K X(t)=A(θ)*S(t)+N(t) (1) 式中,S(t)=[s1(t),s2(t),…,sK(t)]T为K×1维的信号矩阵;N(t)=[n1(t),n2(t),…,nM(t)]T为维噪M×1声向量;A(θ)=[a(θ1),a(θ2),…a(θK)]为M×K维的阵列导向矢量阵,其中a(θi)(i=1,2,…,K)为各信号的导向矢量,具体表达式如下: (2) 假设信号与噪声相互独立,阵列接收数据协方差矩阵为: RX=E[X(t)XH(t)]=ARSAH+RN (3) 式中,RS=E[S(t)SH(t)]为信号协方差矩阵;RN=E[N(t)NH(t)]为噪声协方差矩阵。 对阵列接收数据的协方差矩阵RX进行特征分解,可得: RX=U∑UH (4) 式中,∑=diag(λ1,λ2,…,λM)为特征值构成的对角阵且满足λ1≥λ2≥…≥λM;特征值对应的特征向量构成矩阵U=[e1,e2,…eM]。 色噪声是由各个阵元间的互耦和噪声的相关性,以及各通道内部噪声功率的不同所产生的。其噪声协方差矩阵不再是一个对角阵(与白噪声相比),同时数据协方差矩阵的噪声特征值不再围绕噪声功率分布,导致噪声特征值的发散,进而影响到利用特征值进行信源数估计的相关算法的性能。 通常,数据协方差矩阵展开可得: RX=E[X(t)XH(t)]= ARSAH+2Re(RSN)+RN (5) 实际中,往往采用以下有限次快拍的数据采样协方差矩阵逼近RX: (6) 而当快拍数有限时,数据协方差矩阵的交叉项不再为0,RSN≠0,RN不再为对角阵。因此,有限快拍数增加了信号之间、信号与噪声之间以及各阵元噪声之间的相关性。那么,在色噪声/低快拍条件下,如果直接使用协方差矩阵的特征值进行信源数估计,估计性能不佳。接下来,将在特征值的基础上引入信号子空间与噪声子空间的正交性,提出一种基于加权特征投影的信源数估计方法。 预将阵列接收协方差矩阵RX用分块的形式表达,先将阵列导向矢量A按行分块可写作: (7) 其中: (8) 则阵列接收的数据协方差矩阵可以表示为[16]: (9) 由于信源均互不相关,且RS为满秩的对角阵,故RSbi≠0(i=1,2,…,M)。 在实际应用中,为了保证算法在低信噪比条件下的性能,首先对阵列接收数据协方差矩阵进行预处理。因受快拍数低的影响,噪声所对应的小特征值为非零的较小值,可以选取最小的两个特征值的均值对阵列接收数据的协方差矩阵进行降噪处理,得到新的协方差矩阵: (10) 式中,I为M×M的单位阵。 然后,对降噪后的协方差矩阵进行特征分解: (11) 式中,∑′=diag(μ1,μ2,…,μM)为特征值构成的对角阵;U′=[ξ1,ξ2,…,ξM],ξi(i=1,2,…M)为特征值μi对应的特征向量。将特征值作为对应特征向量的权值,构造了加权空间矩阵G,表达如下: G=U′∑′= [ξ1,ξ2,…,ξM]·diag(μ1,μ2,…,μM)= [μ1ξ1,μ2ξ2,…,μMξM] (12) G是通过特征值μi对特征空间U′进行加权变换得到的加权空间矩阵。 (13) ri=|ρi| =|μiHξiHARSbjH|≤|μiH||ξiHA||RSbjH| = k|μiH||ξiHA|→0(j=1,2,…,M) (14) ri=|ρi| =|μiHξiHARSbjH|≤|μiH||ξiHA||RSbjH| = k|μiH||ξiHA| >0(j=1,2,…,M) (15) 基于以上理论研究和矩阵分析,进行信源数估计,首先定义函数: (16) 式中,k取1,2,…,M,即(13)式中每一行中各元素先开方后求其均值。构造判决函数: (17) 式中,L为快拍数,D(L,M)是一个与阵元数和快拍数有关的调整因子,它在0至1之间选取,与阵元数和快拍数均成正比,阵元数和快拍数越多D(L,M)的取值越接近于1。k取1,2,…,M,所有使Δ(k)>0的f(k)个数即为信源数目。 步骤1:计算阵列接收数据协方差矩阵:RX=E[X(t)XH(t)]; 步骤3:对新协方差矩阵进行特征分解,根据式(12)利用得到的特征值和特征向量构造空间矩阵G; 步骤5:根据式(16),求出M个函数值f(k); 本算法通过对原协方差矩阵进行降噪预处理,该步骤可以降低噪声判据值,从而使算法应用于低信噪比环境中;本方法没有对噪声模型进行特定限制,可应用于色噪声背景下。特别是在划分噪声和信号时,本文提出了进一步缩小噪声的判据值和放大信号的判据值的方法,具体说明如下: 本文方法的计算量包括:对M阶协方差矩阵进行特征分解的计算量约为M3;对M阶去特征的协方差矩阵进行特征分解的计算量约为M3;加权投影部分计算量为2M3,故本文方法的总体计算量为4M3。而经典的GDE算法的计算量集中在M-1阶矩阵特征分解和M阶矩阵酉变换部分。改进盖氏圆算法(MGDE,modified gerschgorin’s disks estimation)与GDE算法相比增加了一次酉变换的计算量。信息论方法的计算量主要集中在M阶协方差矩阵的特征分解和似然函数[7]的计算。如表1所示,将本文方法与信息论方法、GDE算法以及MGDE算法的算法复杂度进行了对比。本文方法计算复杂度略低于MGDE算法,但高于信息论方法和GDE算法。对比信息论算法和GDE算法,本文方法计算复杂度的提升换来了在两种噪声背景下及低快拍、低信噪比条件下的性能提升。 表1 算法复杂度对比 实验设置:仿真采用阵元间距为半波长的7阵元均匀线阵(理论最大检测信源数为6),信源数分别设定为为2个和5个信源,在不同信噪比和快拍下进行200次Monte-Carlo实验,通过成功检测信源数目的概率评价算法性能。 为了验证本文提出算法的有效性,实验在白噪声条件下与AIC准则、MDL准则、GDE准则、MGDE算法和文献[15]算法进行仿真对比,分析不同条件下的算法性能。 实验一:阵元数为7时,在白噪声条件下,依次给出多快拍和低快拍两种情况的信源数目成功检测概率随信噪比的变化情况。仿真条件如下:快拍数分别为100和10,有2个独立信源,分别由-10°和0°入射到7阵元的均匀线阵,阵元间距为半波长,得到成功检测概率随信噪比的变化情况。 多快拍条件下,实验结果如图1(a)所示,可以看出4种算法的成功检测概率均随SNR增大而增大。其中本文算法在信噪比大于-3 dB时信源数成功检测概率达到100%,MDL准则在信噪比为0 dB时信源数成功检测概率达到100%,MGDE算法在信噪比大于1 dB时信源数成功检测概率达到100%,文献[15]的算法在信噪比大于8 dB时,成功检测概率接近100%,AIC准则和GDE准则均低于本文算法,可见本文算法性能在低信噪比条件下略优于AIC准则、MDL准则、MGDE算法、GDE准则和文献[15]算法;低快拍条件下,实验结果如图1(b)所示,可以看出信息论算法受快拍数影响大,性能下降较快。本文算法在信噪比大于2 dB时信源数成功检测概率达到100%,明显高于GDE准则、MGDE算法和文献[15]算法。可见,本文算法在多快拍和低快拍两种情况下都优于其他5种算法。 图1 信源数为2时,白噪声条件下,成功检测概率随SNR变化 实验二:阵元数不足时,在白噪声条件下,依次给出多快拍和低快拍两种情况的信源数目成功检测概率随信噪比的变化情况。仿真条件如下:快拍数分别为100和10,有5个独立信源,分别由-25°、-10°、0°、10°和25°入射到7阵元的均匀线阵,阵元间距为半波长,得到成功检测概率随信噪比的变化情况。 多快拍条件下,实验结果如图2(a)所示,可以看出本文方法的成功检测概率达到100%时的信噪比为9 dB,MDL准则大于8 dB时其成功检测概率近似达到100%但略有波动,文献[15]算法成功检测概率达到100%时信噪比为10 dB但略有波动,AIC准则、MGDE算法和GDE准则其检测性能明显低于本文算法;低快拍条件下,实验结果如图2(b)所示,可以看出当信噪比大于16 dB时,本文算法成功检测概率达到100%,文献[15]算法当信噪比大于16 dB时,成功检测概率达到100%但略有波动,而AIC准则、MDL准则、MGDE算法和GDE准则还未达到。 图2 信源数为5时,白噪声条件下,成功检测概率随SNR变化 实验三:阵元数一定时,在白噪声条件下,为检测算法在不同信源个数下的估计性能,给出了成功检测概率随信源个数的变化情况。仿真条件如下:阵元数为7,快拍数取100,信噪比为15 dB,信源数分别取1至6,信源为来自不同方向的独立信源,得到成功检测概率随信源数变化的情况。 实验结果如图3所示,信源数为1至5时,本文方法、MGDE算法、MDL准则成功检测概率为100%,GDE准则近似100%,AIC准则与文献[15]算法均未达到100%。信源数为6时,AIC准则成功检测概率接近50%,其余5种算法均接近0。可以看出本文方法,牺牲了自由度换取了在不同信源个数条件下较高的成功检测概率。 图3 白噪声条件下,成功检测概率随信源数变化 实验四:阵元数充足时,在色噪声条件下,依次给出多快拍和低快拍两种情况的信源数目成功检测概率随信噪比的变化情况。各阵元产生的色噪声是由高斯白噪声激励一个稳定的ARMA模型产生的[17]。仿真条件如下:快拍数分别为100和10,有2个独立信源,分别由-10°和0°入射到7阵元的均匀线阵,阵元间距为半波长,得到成功检测概率随信噪比的变化情况。 多快拍条件下,实验结果如图4(a)所示,可以看出当信噪比为6 dB时本文算法成功检测概率达到100%,MGDE算法当信噪比为9 dB时成功率达到100%,GED准则当信噪比大于16 dB时成功检测概率为100%;低快拍条件下,实验结果如图4(b)所示,可以看出当信噪比为9 dB时本文算法成功检测概率达到100%,MGDE算法当信噪比为15 dB时成功率达到100%,GED准则当信噪比大于16 dB时成功检测概率为100%。可见,在色噪声条件下,本文算法优于MGED算法和GED准则。 图4 信源数为2时,色噪声条件下,成功估计信源数随SNR变化 实验五:阵元数不足时,在色噪声条件下,依次给出多快拍和低快拍两种情况的信源数目成功检测概率随信噪比的变化情况。同样各阵元产生的色噪声是由高斯白噪声激励一个稳定的ARMA模型产生的[24]。仿真条件如下:快拍数分别为100和10,有5个独立信源,分别由-25°、-10°、0°、10°和25°入射到7阵元的均匀线阵,阵元间距为半波长,得到成功检测概率随信噪比的变化情况。 多快拍条件下,实验结果如图5(a)所示,可以看出当信噪比为10 dB时本文算法成功检测概率达到100%,MGED算法在信噪比为14 dB时成功率达到100%,GED准则在信噪比为20 dB时仍未达到100%;低快拍条件下,实验结果如图5(b)所示,可以看出当信噪比大于11 dB时本文算法成功检测概率接近100%且略有波动,MGED算法在信噪比为18 dB时成功率接近100%,GED准则当信噪比为20 dB时仍未达到100%。可见,在色噪声条件下,本文算法优于MGED算法和GED准则。 图5 信源数为5时,色噪声条件下,成功估计信源数随SNR变化 实验六:阵元数一定时,在色噪声条件下,为检测算法在不同信源个数下的估计性能,给出了成功检测概率随信源个数的变化情况。仿真条件如下:阵元数为7,快拍数取100,信噪比为15 dB,信源数分别取1至6,信源为来自不同方向的独立信源,得到成功检测概率随信源数变化的情况。 实验结果如图6所示,信源数为1至5时,本文方法成功检测概率为100%,信源数为6时成功检测概率下降至0。GDE准则和MGDE算法当信源数变为4时,成功检测概率下降,信源数为6时,成功检测概率下降至0。 图6 色噪声条件下,成功检测概率随信源数变化 本文提出了基于加权特征投影的信源数估计方法,利用降噪后协方差矩阵的特征值和特征向量构建了加权空间矩阵,通过空间投影使得信号判据值远大于噪声判据值,最后通过构建判决函数实现信源数估计。通过理论分析证明了该方法的可行性,并分别在白噪声和色噪声两种情况下进行仿真实验,结果表明本文算法受阵元数目影响较小,且在低快拍、低信噪比条件下也具有优良的估计性能,更适于工程应用。2 基于加权特征投影的信源数估计方法
2.1 阵列接收协方差矩阵分块表达
2.2 加权空间矩阵的构建
2.3 判据值的缩放
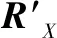

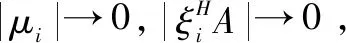
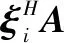

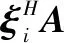
2.4 信源数估计方法
3 算法步骤

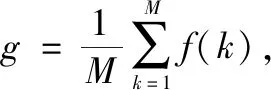
4 算法性能分析说明


5 算法复杂度分析

6 仿真实验
6.1 白噪声条件下仿真分析

6.2 色噪声条件下仿真分析

7 结束语

