改进的ReliefF在ICP特征选择中的应用*

张光普 周从华 张 婷

（1.江苏大学计算机科学与通信工程学院 镇江 212013）（2.无锡市妇幼保健院 无锡 214002）

1 引言

特征选择是人们在机器学习任务中，一个重要的“数据预处理”过程。数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已［1］。通过特征选择，可以将数据集中的冗余数据以及相关性较小的数据清除，在确保特征集合包含所有重要特征的情况下，降低数据集的维度，从而提高学习器的效率和精度［2～3］。

特征选择已经成为医学数据预处理中不可缺少的部分［4～6］。特征选择算法主要有过滤式（Filter）方法和包裹式（Wrapper）方法和嵌入式（Embedded）方法三种。包裹式特征选择方法直接将最终所使用的分类算法或模型的性能作为特征子集的评价标准，在特征选择过程中需多次训练学习器，所以算法计算复杂度高，计算开销会比过滤式特征选择方法大得多，对于样本数少高维度的医学数据并不适用。与包裹式特征选择算法需要绑定后续的学习器不同，过滤式特征选择方法通过数据特征的内在属性来评价特征的差异性，根据差异性评分对特征进行排序，选择合适的特征用于学习器的学习，选择过程中不考虑学习器对特征的影响［7～8］。

妊娠期肝内胆汁淤积症（Intrahepatic Cholestasis of Pregnancy，ICP）是妊娠期严重危害母婴的并发症，其发病率最高可以达12%［9～10］。原始的ICP数据集中含有大量的生物标志物信息，特征间通常会存在相关性，以及在ICP数据的采集过程中，由于设备和人为因素，数据集中往往会存在较大的冗余和噪声，由于ICP患者们存在多种妊娠结局，并且不同妊娠结局间的人数差异较大，使数据集存在一定的不平衡性。

本文针对ICP数据的冗余性及数据不平衡的问题，在ReliefF算法的基础上进行改进，提出了一种新的特征选择算法SC-ReliefF算法，并应用到ICP特征选择当中筛选出对患病影响最大的特征子集。一方面，设计了新的样本选择方法，改进后的样本选择方法根据每个样本与类中心的欧式距离，均匀地从各个类别中各自选择n个样本用来累计权值，从而使ReliefF算法可以更好地应用于非平衡数据当中。另一方面，ReliefF算法去除冗余特征的能力较低，新的算法通过引入调整的余弦相似度用来度量特征向量之间的相关性，有效地去除ICP数据中的冗余特征。SC-ReliefF算法从样本的选择上和去冗余特征两个方面对ReliefF算法进行了改进，使ReliefF算法适用于非平衡数据，同时有效去除原始数据集中的冗余特征。

2 ReliefF特征选择算法概述

Relief（Relevant Features）算 法被Kira和Rendell在1992年提出，用于解决二分类问题，是一种高效的过滤式特征选择算法［11～12］。算法的核心思想是表现好的特征将有利于分类，反之，表现差的特征会对分类产生不利影响。该方法通过比较样本在某个特征上的猜中近邻与猜错近邻的距离大小，来确定该特征对分类是否有利，同时赋予该特征一个权重。最后，指定一个阈值，剔除权重小于阈值的特征即可。

设样本集T=｛（x1，y1），（x2，y2），…，（xn，yn）｝，每个样本中存在k个特征，xi=｛xi1，xi2，…，xik｝，两个样本xa和xb在特征j上的距离表示为

若特征j为离散型，

若特征j为连续型，

由于Relief算法只能处理二分类问题，Kononenko在1994年对Relief算法进行了改进，得到ReliefF算法，改进后的算法可以处理多分类问题。

假设数据集T=｛（x1，y1），（x2，y2），…，（xn，yn）｝，T中包含n个样本以及m（m＞2）个样本种类m（m＞2）个，随机从数据集中选取样本xi，若样本属于第k类（1≤k≤m），与Relief算法类似，ReliefF算法首先在第k类样本中找到d个xi的最近邻样本，并将其放入集合N，记为猜中近邻集合，然后在除k类之外的每一个类别的样本中分别找出d个xi的最近邻样本，并将其放入集合M（l）记作（l=1,2,…,m;l≠k），记为，猜错近邻集合。则xi与猜中近邻在特征j上的距离表示为

则xi与猜错近邻在特征j上的距离表示为

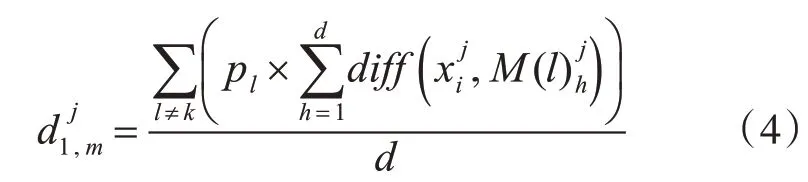
其中pl=nl/n，表示第l类样本在数据集T中所占的比例。M（l）h表示第l类样本中第h个样本。

则特征j的权重Wj计算公式为

通过分析式（3）～（5）可以得出，ReliefF算法通过计算样本xi的d个猜中近邻与其异类l中的距离xi最近的d个样本在特征j上的平均距离，并将平均距离进行加权平均，即可得到样本xi与l类在特征j上的距离。最后在xi的所有异类上进行此操作得出xi与异类样本在特征j上的距离差异。由此评价该特征区分类别的能力。

3 对ReliefF算法的改进

3.1 样本的选择

ReliefF算法采用随机的方式从训练样本中重复选取m个样本，由于m一般远远小于样本量，这就要求所选择的m个样本尽量均匀地分布在每个类别的样本空间中，从而使m个样本能够更加有效地评估各个特征的权重。但在实际的ICP数据集中，ICP患者们有多种可能的妊娠结局，患者在各个ICP妊娠结局上的分布存在较大差异，若果采用这种随机选取样本点的方式，这必然会导致［13］：

1）特征的权重会向样本数量多的类别倾斜。

2）随机挑选所带来的另一个问题是算法的不稳定性。

针对上述两个问题，本文对ReliefF中的样本选择方法进行了如下改进得到SRelifF算法。

在抽取样本的时候，将从每个类别的样本中个抽取m个样本，避免随机采样时，少数类样本被选择几率过小的情况。

1）首先通过式（6）计算样本k类样本中心：

其中，classk代表k类样本的集合，nk表示k类样本的个数。

2）通过式（7）计算每个k类样本距离样本中心的距离：

3）将k类中每个样本按照与样本中心距离大小从小到大排序，按照间隔Δd=nk/m等间隔地选取m个样本作为特征权重累积样本，放入集合Dk。

结合上述样本选择方法对ReliefF算法改进得到SReliefF算法，改进之后的样本选择方法一方面可以保证均匀地从各个类别样本中选择相同数目的样本进行特征权重的累积计算，一定程度上避免了ICP数据集的不平衡性对ReliefF算法带来的影响。另一方面，由于样本不是随机选择的，那么只要样本集合没有发生变化，选择的样本都是固定的，所以每次运行ReliefF算法得到的特征权重是稳定的，从而提高了算法的稳定性。

3.2 特征之间的相似性

SReliefF虽然能够用于非平衡数据集的特征选择，但仍然存在着以下问题：SReliefF算法并没有考虑到特征之间的相关性，这不可避免地会造成选择之后的特征子集存在一定的冗余性。本文引入余弦相似度作为特征相似性的度量进一步在特征子集中剔除冗余特征［14］。

余弦相似度通过测量两个矢量之间角度的余弦来测量两个矢量之间的相似性［18］。

余弦相似度的计算如式（8）所示：

其中，A和B为向量，余弦相似度s（A，B）衡量了两个向量之间的相关性程度，其值越大代表两个向量之间的相关性越强。将特征向量表示为Fi和Fj，利用余弦相似度作为特征相似性度量，得向量Fi和Fj的相似度：

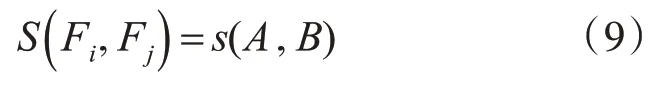
根据式（9）推得Fi与特征集合F之间的冗余度：

式（10）中，||F代表特征集合F中所包含的特征总数，Fj为特征集合F中的特征，结合式（10）和式（9）得特征集合F的冗余度计算式：

SC-ReliefF算法的基本思想是：首先利用SReliefF算法剔除相关性较小的特征得到特征子集F，然后通过特征集合评价函数进一步在特征子集F中进行去冗余操作，最终得到Fend。得到特征集合的评分函数：

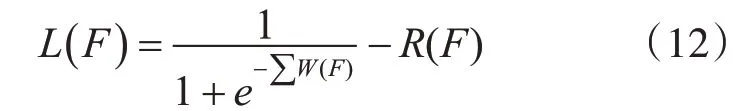
SC-ReliefF算法主要步骤：首先通过SReliefF算法得到特征集合相应的权重向量，并对向量中的各个权重分量从大到小排序，按照设定的阈值对特征集合进行初步筛选。然后进行特征子集搜索，搜索方式为序列向前搜索：每次移除特征集合中权重最小的特征，通过评分函数计算删除该特征后特征集合的评分，并与原特征集合评分进行比较。SC-ReliefF的具体步骤如表1所示。

表1 SC-ReliefF算法

其中，fi代表权重排序第i位的特征。此外，算法在序列向前搜索过程中加入评分因子η，表示在删除第i位特征后，评分至少提升η才能将该特征删除并放入候选集合，否则保留该特征，继续搜索特征集合。

SC-ReliefF算法根据特征权重和冗余度度量共同构建了特征集合的评价函数，使用序列向前搜索的方式进行子集的搜索与生成，从整体角度对特征子集进行评价，且加入评分因子，控制特征子集规模，可以分析不同规模的特征子集的优劣。最后，本文通过实验验证了SC-ReliefF算法在不会降低分类算法性能的基础上，可以去除冗余特征，得到规模较小且有效的特征子集。

4 实验分析

4.1 实验信息

本次实验数据由无锡市妇幼保健院提供，包含400名患者和300正常人的相关数据，根据患者的妊娠结局可分为胎儿窘迫、新生儿窒息、早产、羊水污染四种。

本实验采用精度（Acc）、宏差准率（macro-P）、宏查全率（macro-R）以及相应的宏F1（macro-F1）作为分类算法的性能度量方式。

4.2 实验结果及分析

本实验使用ReliefF、mRMR、RS-ReliefF［15］特征选择算法以及本文提出的SC-ReliefF算法对ICP数据集进行特征选择，然后利用BP-NN、SVM进行分类。实验使用十折交叉验证法，本实验通过比较在分类器取得最佳精度的条件下，特征选择算法选择的特征子集规模以及学习器的其他性能，验证SC-ReliefF算法的有效性。

本节实验选取四种特征选择算法所选取的不同规模的特征子集，子集范围从10%～100%，并利用BP-NN、SVM分类器，利用十折交叉验证算法在不同子集规模下分类器的分类性能。图1和2为四种特征选择算法选择不同规模特征子集在BP-NN和SVM分类器上的平均分类精度。

图1 四种算法在BP-NN上的对比

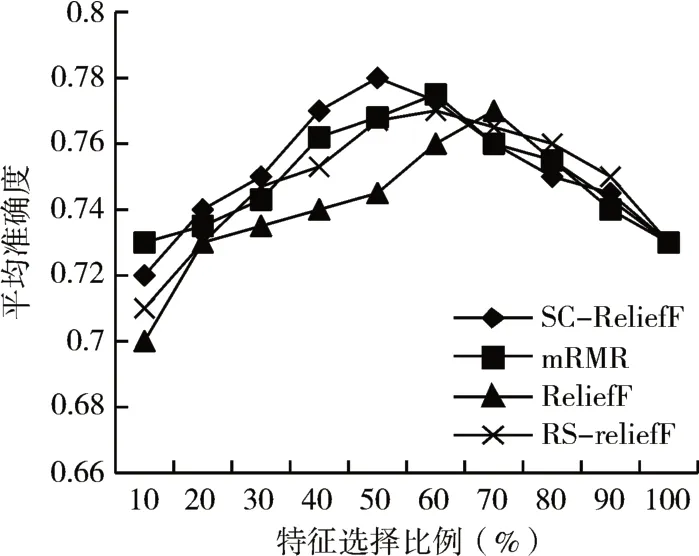
图2 四种算法在SVM上的对比

由图1可知，在BP-NN上，所提算法SC-ReliefF在50%～60%的特征选择比例下平均准确度可达0.8，然后随着特征子集规模逐渐增加，算法准确度逐渐下降。而相对于原始的ReliefF算法，算法直到选取70%～80%的子集规模时，且精确度最高只有0.78；RS-ReliefF是另一种最ReliefF改进的特征选择算法，在选取规模在60%～70%时，最高平均精度可达0.78；mRMR特征选择算法在选取规模为60%～70%之间时，最高分类精度可达0.79。在SVM分类器上也有类似规律，算法性能明显优于对比算法，在50%～60%区间内有较大提升。结合四种特征选择算法在两种分类器上的表现，说明本文所提出的算法能有效去除冗余特征，使得算法在较小的特征规模下，尽可能取得优秀的性能。

本文在取四种特征选择算法在取得最佳平均分类精度的情况下，综合其他分类指标进行进一步对比，如表2所示。

表2 四种算法性能参数对比

由表2可知，本文所提的SC-ReliefF算法相较于传统的ReliefF算法，所选择的特征子集在两种分类器算法上的性能均有明显提高。此外在与RS-ReliefF和mRMR两种ICP特征选择算法相比，改进后的算法在多数情况下有着更好的性能。实验结果说明，本文提出的SC-ReliefF算法可以选择出较小规模的特征子集，且对学习器性能有略微提高，证明了SC-ReliefF算法在ICP特征选择中的有效性。

5 结语

本文针对ICP数据集普遍存在的高冗余和非平衡性的特点，对传统的ReliefF特征选择算法进行适应性改进。改进了ReliefF算法的样本选择算法，通过类内平均距离均匀地从各个类别选择样本，一定程度上消除非平衡性带来的影响。随后在此基础上，以余弦相似度作为特征冗余的度量进一步去除冗余特征，提出了一种结合余弦相似度的ReliefF的特征选择算法——SC-ReliefF算法并用于ICP特征选择中。实验结果表明，SC-ReliefF算法能够在提升学习器整体性能情况下，选择出规模更小的ICP特征子集，从而提升学习器的效率。本文后续工作将集中于如何更好地衡量特征间的冗余度以及提升学习器的分类精度两个方向上。