基于问题意识，发展学生的提问能力

钱小燕

[摘 要]提问是数学课堂教学中的重要活动，是师生之间、生生之间进行信息沟通、情感交流和教学反馈的主要手段。然而，在体现学生主体地位、把学生推到前台时发现，学生的问题意识不强，提问能力弱，更别谈创新精神、素养的提升。从问题意识出发，营造氛围、激发兴趣、教给方法，让学生想提问、敢提问、能提问、会提问，进而发展学生的提问能力。

[关键词]问题意识;提问能力;教学

新课标中指出，独立发现问题和提出问题是培养学生创新精神的基础。问题是思维的起点，是创造的前提，是深度学习的开始。可现实的困境是，学生不会提问、不敢提问。鉴于此，笔者以问题意识为立足点，探讨如何引导学生发现问题、提出问题，帮助学生树立问题意识，发展学生的提问能力。

一、创设问题情境，让学生想提问

教学中，教师可以结合教学内容创设有新意、有趣的问题情境，让问题寓于情境之中，激发学生探究的兴趣，使学生全神贯注地学习数学知识。教师可以利用新旧知识的结合点、故事、数学典故等来创设问题情境，并且这些问题情境以悬念、矛盾、质疑、开放等形式来表现会更有效。

比如，在“认识方向”的导入环节中，教师在给学生讲述“南辕北辙”的故事后提问：“大家听了这个故事有什么想说的吗？”有的学生回答：“这个人走的方向是反的！”教师说：“对啊，他在朝着与楚国相反的方向狂奔，只能离楚国越来越远。这个故事告诉了我们什么道理呢？这个故事的题目是一个成语，你们知道是什么吗？”有的学生回答：“做事要找到正确的方向。这个成语叫‘南辕北辙。”教师继续讲道：“生活中还有很多与方向有关的成语，如东奔西跑、南征北战等。”有的学生问：“怎么分东、西、南、北呢？”教师由此自然地引出新课内容：“今天我们就来学习新知识‘认识方向……”

二、营造和谐氛围，让学生敢提问

学生提出的问题是经过思考的，虽然不同学生有各方面的差异，提出的问题的层次也参差不齐，但都是思维的产物。教师要尊重学生提出的问题，对学生的问题不要轻易进行判断，而要充分给予认同，要用爱来营造自己人格魅力的磁场，将学生吸引到自己的周围，让学生对教师产生亲切感、信任感。教师不仅要自己率先垂范，而且要要求学生对他人的问题做出积极回应。在学生提问受阻的时候，教师要引导学生多问问：“对于今天的学习内容，你有什么问题吗？知道了这些后，你又想到了哪些问题？”长此以往，才能营造良好的提问氛围，让学生感到课堂其实是自由的，能够毫无顾虑地提出自己的所想所思，从而使学生的问题意识如花朵般绽放。

三、创造对话条件，让学生能提问

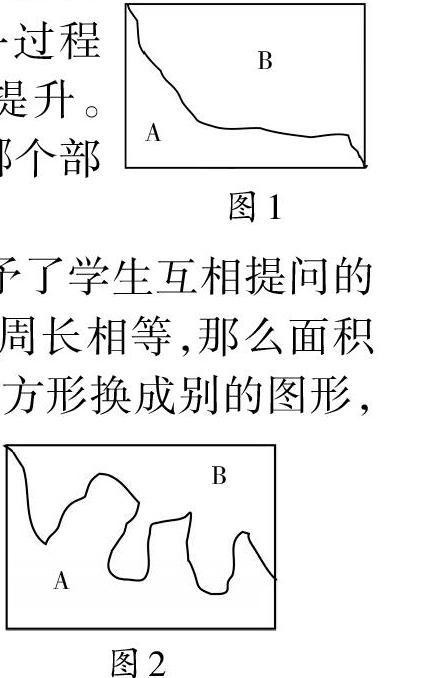
实践证明，学生与学生之间的对话更能调动学生提问的积极性和主动性，特别是在小组合作模式下，每个学生都会为了集体荣誉积极思考，努力寻找解决方法。在这一过程中，学生的问题意识得到有效提升。比如，如图1所示，A、B两部分，哪个部分的周长长一些？

教师在这道典型问题下，给予了学生互相提问的时间。一个学生提问：“A和B的周长相等，那么面积呢？”另一个学生提出：“如果把长方形换成别的图形，比如三角形，或者圆形，A和B的周长还相等吗？”还有学生画出了图2，并提问：“这时候A和B的周长相等吗？如果不相等，哪一部分的周长长呢？

学生之间相互提问，加深了学生对图形周长的认识，学生打开了思路，问题意识在不知不觉中得到了发展。

四、给予方法指导，让学生会提问

在课堂教学中，有的学生找不到思考的方向;有的学生对某些问题有自己的想法，但是受语言表达能力等因素的限制，不能准确表达自己的想法，或者脱离教学内容，词不达意。基于此，在问题意识培养的过程中，教师要教给学生提问的方法，让学生更有效地参与到学习中来。

1.倾听同伴的见解，针对疑惑提问

在与同伴交流时，要注意倾听对方的方法，提出自己的疑问和观点，同时把自己的方法与同伴的方法进行比较，思考自己的方法有哪些可改進的地方。

比如，“多边形的面积”单元的一道练习题：把一张长50厘米、宽10厘米的长方形纸剪成底是8厘米，高是5厘米的直角三角形，可以剪多少个？教师发现，绝大部分学生都是用长方形的面积除以三角形的面积，得出一共可以剪25个。在小组交流环节中，有学生提出：“长方形是不是正好都剪成了三角形呢？”马上有学生回应：“把直角三角形看作长8厘米、宽5厘米的长方形，这个长方形的长里面正好可以剪出10个5厘米，宽可以剪出1个8厘米，还余下2厘米，总共可以剪出10个长方形，也就是20个三角形，余下的2厘米剪不出符合要求的三角形。”部分学生对这种方法表示认同，发现长方形不是正好都能剪成三角形。

2.比较各自方法，针对异同质疑

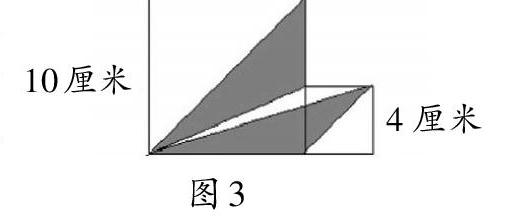
教学中，教师要注重引导学生通过比较方法的异同，揭示知识的本质。比如计算图3中阴影部分的面积，一共出现了三种方法。

方法一：分别算出两个阴影三角形的面积，再相加。方法二：先算两个正方形面积的和，再算出三个空白三角形的面积，最后用正方形的面积减去空白三角形的面积。方法三：10×10÷2=50（平方厘米）。

教师将三种方法一起呈现在黑板上，让学生进行比较。

生1：方法三好简便，为什么可以这样算呢？

生2：这三种方法各有怎样的特点呢？

生3：在什么样的情况下可以用第三种方法呀？

学生在不断的追问中逐步明晰，方法一最直接，但是要先算出上面一个三角形的底;方法二拐了个弯，不直接算阴影部分的面积，而是借助空白部分的面积算阴影部分的面积，但是每个三角形的底和高都是已知的，不需要去算;方法三虽然简便，但是要用到转化方法，思维难度大一些。通过三种方法的比较，学生在不停地追问中实现了思维的进阶。

3.链接相关知识，联想产生问题

许多新知识都是从旧知识生长起来的，教师要引导学生找出知识的生长点，并由此出发，思考以下问题：（1）知识A和知识B之间有什么联系？（2）知识A和知识B有哪些相同点和不同点？（3）A的方法也适用于B吗？

比如在复习“简便计算”这部分内容时，有学生提出：“乘法有乘法分配律，除法为什么没有除法分配律呢？”

生1：因为会影响计算结果。比如12÷（1+3），如果用除法分配律就是12÷1+12÷3=12+4=16，而正确结果是3。

生2：可是当（a+b）÷c的时候又是可以的呀。

生3：（a+b）÷c之所以可以使用分配律，是因为除数只有一个数，可以保证无论如何除数的倒数不会变。而a÷（b + c）的除数是一个算式，所以不可以使用。

在相互提问与探究中，学生加深了对分配律的理解。

总之，学生问题意识的培养、提问能力的提升不是一蹴而就的，需要一个长期的、有计划的锻炼过程。教师要在各个环节创造提问机会，以调动和激发学生提问的积极性，使学生主动地提出问题。

（责编 黄 露）