小数乘除法的算理剖析

吴静环

[摘 要]计算教学中，教师往往出示几个例题，引导学生观察归纳出运算法则和性质后就让学生进行大量应用训练，这样一来，几道题的解题训练就可以起到立竿见影的效果，因为教师给的题目基本上都是设计好数据的，非常好算。实践证明，没有专项的计算训练，没有深入的算理研究，学生就不会有过硬的计算技能。

[关键词]小数; 乘除法;算理

计算是所有小学数学知识得以顺利运用的前提，是构建数学知识框架的基石和钢筋。由于教材中对计算教学的设计非常简略和零散，因此有些教师认为，所谓计算教学，无非是一些数据的简单叠加融合或者分离削减，也就是加减乘除的运算，技术含量较低，只要遵循运算顺序按法则计算，就不会出纰漏，从而对计算的内涵和性质视若无睹，缺少必要的钻研，客观上降低了计算教学的门槛。在本校举办的学生计算能力普查中，这一严峻的问题更是暴露无遗，引起全校数学教师的重视和警惕。

一、直击易错题，寻找原因

笔者对学校五年级学生进行检测，在分析测评卷的过程中，惊奇地发现“0.25÷0.1○0.25×9”这道题的错误率竟高达76.7%。一道判断大小的常规题，错误率却高得出奇，令人始料未及。随后笔者询问了受试的全体学生：“0.25÷0.1○0.25×9，左右两边的算式的值都能精确计算出结果，你觉得哪边大哪边小？给出你的理由。调查结果显示，学生多半是连估带猜，凭着对乘除法的基本意义妄加揣测，无端臆断——除法就是将总数平均分成若干份，求一份是多少，所以平均分之后只会越分越少;而乘法则是除法的逆运算，刚好相反，是将若干份等量的物品合并起来，是扩倍、累加的过程，是一个聚少成多的操作，因此数据会暴增，毫无疑问，上述式子左边的结果小于右边的结果。

学生为何会如此武断地下结论？笔者随后梳理和归整了教材中所有有关乘除法的知识（如表1）。

分析表1不难发现，五年级所学的小数乘除法是对整数乘除法的延伸和拓展，认识难度和思维含量有所增加，乘除法的计算结果不再限于整数范畴，已经引申和扩散，一直拓宽到小数、分数领域，认识也更加细化。解答此题时，学生是直接将整数乘除法运算意义生搬硬套移植到小数乘除法中，这属于负迁移，说明学生对小数乘除法的意义没有深刻认识，仅仅是凭借个人想当然的理解来揣度，而课堂教学中教师又没有及时解析和点拨，所以才使得上述错解的集中出现。

二、利用题组对比辨析

奥苏伯尔的认知同化理论指出：人类学习新知的过程实际上是新旧表象相互磨合兼容的过程，学习者必须努力捕捉到原有知识结构中能够融合新知的接口，这里的“同化”指的是求知者把新知一步步导入原有知识结构中，从而补充和完善知识结构。学习者能否顺利吸纳新知，很大程度上取决于原有知识结构中是否存在天然的与新知的某种“亲缘关系”。照此理论，教师必须在教学新知前查清学生原有知识结构中存在哪些“近亲因子”，并据此开展教学活动。教师在教学时倘若做好了充分的学情分析，精准把握教材，错误应该可以避免。

综合以上分析，筆者认为应从以下两方面加强教学。

第一，准确把握教材，合理灵活运用。倘若仔细研究教材，不难发现北京版教材五年级上册第7页的第7题和第24页的第8题分别对整数乘除法和小数乘除法进行了对比辨析：第7页的第7题让学生通过计算，对比得出：一个数乘以纯小数，积比这个数要小。

苏教版教材五年级上册第24页的第8题，也有异曲同工之妙。通过对比发现，被除数为任意一个正数，除数大于1时，商小于被除数，即越除越小;除数小于1时，商大于被除数，即越除越大。从学生的错例可以管窥出教师把握教材的重要性。只有深入透析教材，准确把握其学科精神实质，才能成功帮助学生构建知识体系。这就意味着教师在平时教学中要注重新旧知识的对比辨析，使学生看清形式上的相似与本质上的区别。

三、自创题组直击本质

奥苏伯尔曾提出融会贯通的学习法，该理论认为教师在演进分化出新知的同时，还要注重分化出的各个分支之间的横向关联，要及时为学生打通新旧知识的隔膜，揭破其区别和联系，防止由于知识表现形式的不同而引起的对相同本质的无端猜疑，促进新旧知识的“和平共处”。就小数乘除法的教学来说，笔者认为可以编制关联度明显的对比题组来点破知识间的连接点，让学生捕获知识的转化接口，运用同化和顺应的理论，帮助学生全面掌握知识，自主建构知识系统。

提问：在得数栏里圈出所有的7.2。为什么乘数不同，所得乘积都是7.2呢？

预设1：以第一列算式为参照，第二列算式的两个因数分别缩小至原来的[110]，积就缩小到原来的[1100]，所以积是7.2。

预设2：计算小数乘法时，先忽略小数点的存在，把小数视为整数来计算，算出整数积后清点因数中的小数位数，再在整数积中从右至左点出几位小数。

总结：小数乘法的算理算法来源就是积的变化规律。

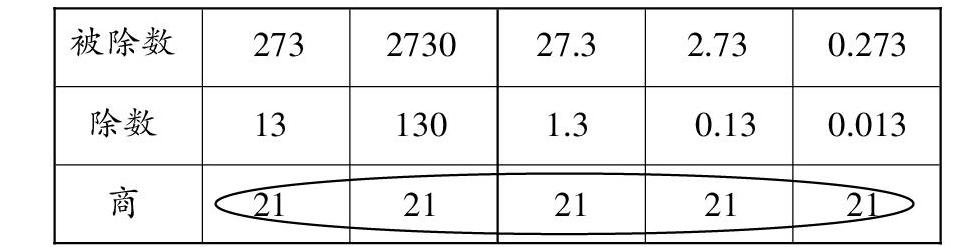
学生先以第一列的算式为参照，填出其他各列所缺失的数字。

提问：观察这些数据，你有哪些疑问？

预设1：被除数、除数各不相同，但是为什么商始终是21呢？

预设2：商恒等于21，你有什么想法？（指引学生发现小数除法的算理：利用商不变定律，将小数除法转化为整数除法，求商后根据商的通用性，将整数商直接挪用作小数商。）

提问：明明一个是乘法，一个是除法，但为何计算结果偏偏相同，其中有何奥妙呢？被圈定的两列数，一个是除数，一个是乘数，各有什么关联？（指引学生发现：两个数的乘积都是1）

预设：1÷0.1，将除法算式转化成乘法算式1×10，除以0.1就相当于倒过来扩大10倍;1÷0.01，将除法算式转化成乘法算式1×100，除以0.01就相当于倒过来，扩大100倍;1×0.5，将乘法算式转化成除法算式1÷2，乘以0.5，就相当于倒过来缩小2倍。这就完美地解释了一个数（不是0）除以纯小数，所得的商为什么反而比被除数大，而乘一个纯小数，所得的积反而比被乘数还要小。

总结：从上述题组的解答中，可以明显感受到转化思想的强大作用。

综上所述，教师对学生的错误不能回避，应深入了解学生的计算功底，找准错因，追根溯源，从而改进教学方法，做到因势利导、循循善诱。

（责编 黄春香）