机电复合传动系统扭转振动主从控制方法*
张 伟,刘 辉,张 勋,张万年,王 珍,严鹏飞
(北京理工大学机械与车辆学院,北京100081)
前言
功率分流式混合动力汽车(HEV)以其高效率和良好的动态性能而备受关注,近年来已成为混合动力汽车领域的研究热点。图1所示为一种典型的双模式功率分流混合动力车辆结构简图,该车辆的核心结构是实现功率分流功能的机电复合传动箱(EMT),该传动箱外部与内燃机、车桥、电力驱动部件相连接,在传动箱内部集成了3个行星齿轮组(PG1,PG2,PG3)和两个动力电机(电机A、电机B),一个离合器和一个制动器。发动机与PG1的行星架齿轮啮合,电机A与PG2的齿圈以及蓄电池的逆变器连接。PG1的太阳轮和齿圈分别连接在PG2的太阳齿轮和行星架上。此外,电机B与PG3的太阳轮相连。输出轴连接到PG3的行星架上。通过变速器中的制动器和离合器的接合或分离,可以实现两种不同的混合驱动模式切换。在第1种模式下(EVT1),制动器接合,离合器分离,EMT输出驱动转矩相对较大,但输出速度较低,只能覆盖车辆的低速范围。当车辆加速到更高的速度时通过操纵液压阀使离合器接合并使制动器分离,EMT切换到第2个模式(EVT2),车辆可以更高的速度行驶,由于受到发动机功率的限制,EVT2输出的最大驱动转矩随着车辆速度的增加而减小。在车辆行驶的整个车速区间内,两种驱动模式根据车速进行切换,从而实现EMT无级变速。发动机与车辆运动是解耦的,通过控制传动比,能够使发动机始终运行在燃油效率最高的工作区间[1]。
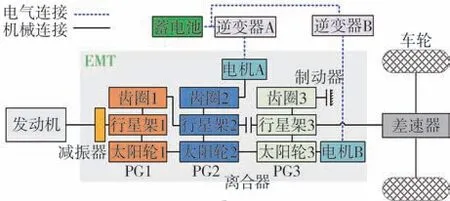
图1 双模式功率分流混合动力车辆结构
随着机电复合传动系统相关研究的广泛、深入开展,研究方向逐渐从结构设计、系统能量管理[2]等方面向动态协调[3]和舒适性提升等方面拓展。在舒适性研究上,学者们一方面研究发动机起停[4]、模式切换[5]等瞬态过程,聚焦减小动力传动系统运行中的冲击度[6],另一方面,精准而全面地分析系统振动特性,致力于改善系统的振动响应[7]。
利用电机的作动能力降低EMT系统的低频扭振是提升HEV性能的重要途径。由于并联式混合动力汽车结构简单,其动力学特性分析及控制相对容易,因而基于电机控制的车辆扭转振动控制首先取得进展,出现了许多实用的控制算法。Cauet等[7]利用多正弦持续扰动的内模原理,设计了一种线性变参数控制策略,实现了发动机脉动转矩的1阶和2阶转速振荡减小。Davis等[8]提出了一种用于分析内燃机转矩的分析模型,得到波动转矩的快速计算方法,利用集成式起动电机产生反向波动转矩来对发动机转矩波动进行补偿,从而实现转矩脉动抑制。
然而,动力分流变速器的复杂结构使得动力总成系统的动力学分析变得困难[9-10]。功率分流混合动力汽车动力源数量更多,动力作用以及振动传递路径更复杂,使得振动主动控制的实现变得极为困难。Zeng等[11]根据非线性观测器和基于模型的转矩估计器的原理,设计了一种基于预测模型的动态协调策略,实现了EVT模式到EV模式的平稳切换,但该控制策略不适用于持续振动过程。Zhang等[12]设计了一种基于电机电流谐波注入的前馈补偿控制算法,利用谐波电流的力矩效应来抵消发动机的转矩脉动。然而,动力分流混合动力汽车的实时转矩脉动很难准确识别。Chen等[13]考虑了发动机起停主动阻尼振动时的惯性效应,但是忽略了行星齿轮的惯性效应。
基于自学习算法的主动阻尼方法是一种振动主动控制中常用的方法,具有很好的自适应能力,对模型参数的变化不敏感。Rafal等[14]针对模式转换控制问题,提出了一种新的高效模式转换控制方法和自适应双环控制框架。FxLMS算法是受迫振动主动控制中最著名的算法,因为它可靠且易于实现。FxLMS算法在噪声主动控制中有广泛应用的研究[15],该控制算法也被用于飞机的振动主动控制[16]。
本文中研究对EMT系统危害性较大的低频扭转振动及其控制策略。针对EMT低频扭转共振,聚焦低阶共振区扭振削峰,基于双电机做动,首创了主从电机控制方法,提出了杠杆比概念,分析了杠杆比对系统共振点的影响。设计了基于PID算法的HEV扭振主动控制算法,仿真结果表明,该控制算法可消除一个或多个共振点,对系统两个低阶扭转共振幅值具有显著的抑制效果。
1 EMT系统扭转振动动力学建模
EMT机械系统的建模忽略了扭转刚度较大的轴和齿轮啮合效应,同时假设齿轮为刚体、离合器和制动器在正常运行时不发生滑摩现象。
根据对某重型双模功率分流式混合动力车辆的台架试验数据分析,建立了混合动力汽车的集中参数多体旋转动力学模型,如图2所示。该模型抽象出了4个扭转弹簧-阻尼元件和16个集中质量的旋转惯量盘。
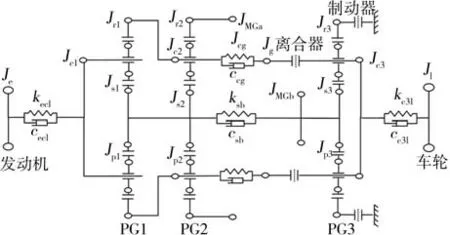
图2 多自由度集中参数动力学系统模型
图2为功率分流式HEV动力学模型,J是EMT中各部件的惯性矩。其中下标e代表发动机,MGa代表电机A,MGb代表电机B,s代表太阳齿轮、c代表行星架、r代表齿圈,p代表不同行星齿轮组的行星齿轮,l代表等效到车轮的车辆负载。kpq和cpq(p,q=e,l,a,b,si,ci,ri)分别代表系统中主要柔性元件的刚度和阻尼。
由于Jr1-Jc2,Js1-Js2,Jr2-JA,Js3-JB之间由机械硬连接,所以有式(1)所示的运动约束。

式中θ为旋转惯量绕旋转轴线旋转的角度。
根据刚体行星轮系运动关系,可得式(2)所示的运动约束。
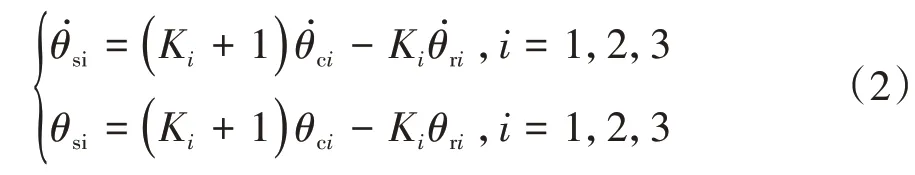
式中Ki为行星轮系特性参数,Ki=Zr∕Zs,Zr为齿圈齿数,Zs为太阳轮齿数。
系统运行时,离合器和制动器有且仅有一个处于闭合状态,有以下运动约束:
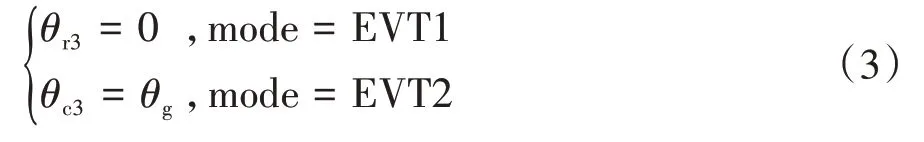
将式(1)、式(2)和式(3)联立,可消去10个关联自由度,系统独立自由度数量变为6个,以系统独立自由度为广义坐标构建状态变量x,得到x=[θe,θc1,θma,θg,θmb,θl]T,即独立自由度为发动机、行星架1、电机A、离合器主动端、电机B和输出轴端的转角。
以系统驱动力矩和负载力矩为外力,可得到系统广义坐标x对应的广义外力为Q=[Te0Tma0TmaTo]T。
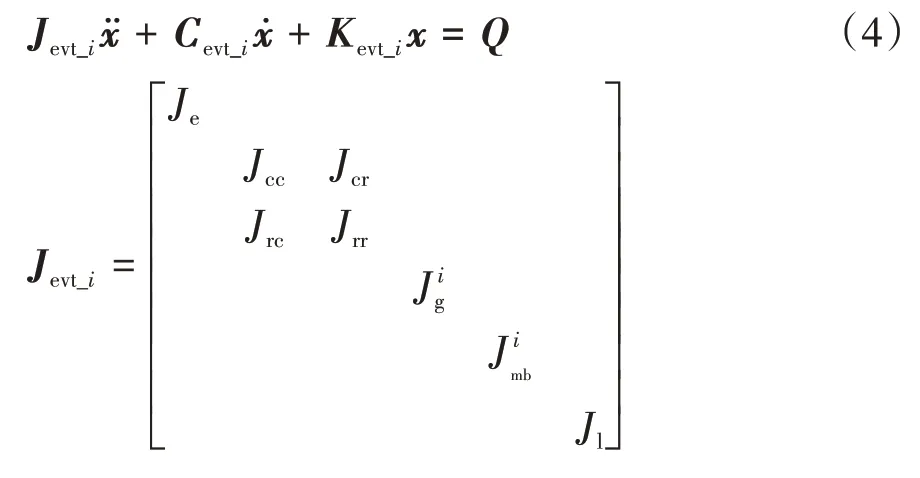

其中:

2 EMT系统扭振特性
EVT1模式和EVT2模式的4个低阶非零模态频率如表1所示。
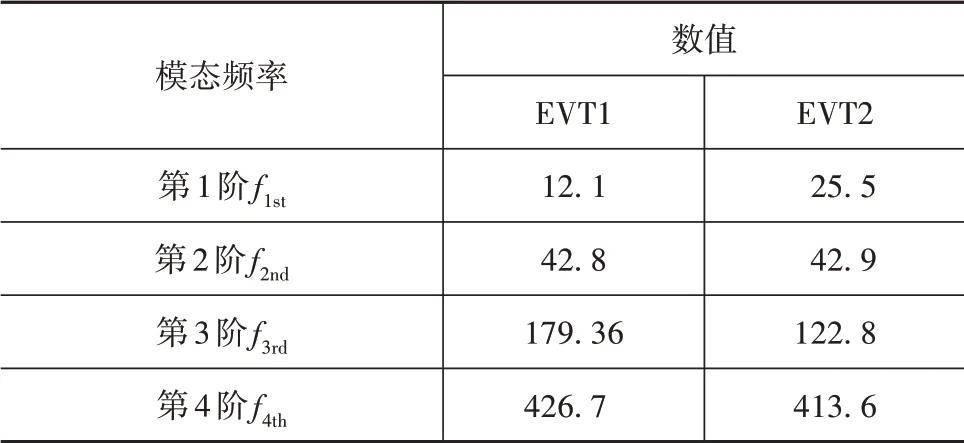
表1 EMT扭转振动固有频率 Hz
由式(4)系统矩阵方程可知,惯量矩阵J非对角线元素出现了非零数,对应于行星齿轮系PG1、PG2的位置,因此EMT系统具有惯性耦合特征。分析刚度矩阵K可知,该矩阵稀疏度较低,在行星齿轮系PG1、PG2的位置刚度耦合程度较大。
行星齿轮组的功率耦合结构导致该系统惯性耦合与刚度耦合程度较高,因此,系统动力学响应复杂,控制难度较大。
由系统模态频率分析可知,2个零频率模态代表系统两种不同形态的刚体运动,刚体运动模态决定了系统稳态运行工况的转速关系。EVT1和EVT2两种模式对应的刚体运动方程如式(5)和式(6)所示。

受工作过程中气缸压力波动和惯性力矩的影响,活塞式内燃机实际输出转矩波动较大。发动机飞轮输出力矩脉动是传动系统扭振的主要激励源,其中低频波动分量对系统性能影响较大。
EMT系统独立自由度转速响应受发动机力矩波动激励的幅频特性如图3所示。

图3 转速波动幅频特性
对比图3(a)和图3(b)可知,EVT1和EVT2的频率响应特性在第1阶和第3阶模态频率附近显著不同,其中离合器主动端和电机B的振动形态发生了突变,结合图1可知,产生这一现象的机理是模式切换导致结构突变。
3 EMT系统扭转振动主从控制
3.1 控制架构
在EMT系统动力学控制中含两个控制目标,一是基于系统刚体运动状态,调节各动力元件的转矩值达到目标转速,满足系统功率分配需求;二是基于扭转振动状态,施加电机力矩的动态力矩值,抑制扭振幅值。
对于由发动机转矩脉动激发的系统扭转共振,可以采用驱动电机(电机A和电机B)进行补偿和控制振动。因此,EMT系统双电机控制结构框架如图4所示,控制系统采用串级控制,外环转矩目标由整车控制器计算,内环为扭振控制,扭转振动的特点是频率较高。在扭振激励时间尺度下,认为外环的转速和转矩相对平稳,属于静态控制。
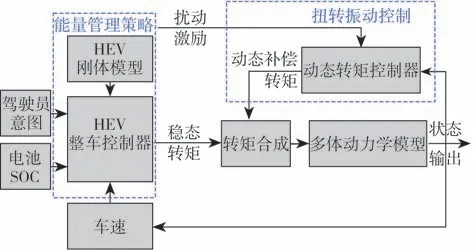
图4 EMT扭转振动控制框图
前馈补偿是振动控制的有效手段之一,但传统的前馈补偿控制要求脉动转矩的精确测量,对变速器动态特性依赖性较强。这些要求在现实中往往难以满足。在真实的运行工况中,转速信号是最容易获取和值得信赖的系统状态测量信号。利用转速信号进行反馈控制是EMT扭振抑制的基本手段。
3.2 主从控制
为满足时域控制的同步性保证系统在各种扭振状态下控制力矩TA和TB的相位不偏移,采用主从控制方法(M-SAC),以其中一个电机力矩为系统主导扭振抑制力矩,以另一个电机力矩为从属扭振抑制力矩,两电机互为主从关系,如图5所示。

图5 EMT扭转振动主从控制(M-SAC)简图
本文中假设A电机为主导,则B电机为从属,两者满足:
Tmb=kabTma
由图5可知,扭振主动控制力矩TA和TB在系统中的作用如同一个虚拟杠杆u,因此定义系数kab为杠杆比。假设主导电机采用PID控制,即

式中:kp为比例控制系数;ki为积分控制系数;kd为微分控制系数。
若发动机动态激励力矩为w(t),则基于主从控制的系统闭环方程为
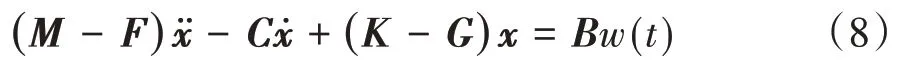
其中:

令w(t)=0,可得主从电机控制方法的系统闭环动力学特性。系统特性由主从控制参数杠杆比kab和PID控制参数kp、ki和kd共同决定。PID控制器参数采用优化方法获取,kp=30,ki=300,kd=1500,系统特性随杠杆比kab变化。
采用数值计算方法得到杠杆比对系统自然频率的影响规律,如图6和表2所示。
由图6(a)和表2可以看出,EVT1模式中,随着kab增大,第1阶模态频率f1st和第2阶模态频率f2nd在交点1处重合,在交点3处分离,因此当kab取值在(0.77,1.04)区间时,f1st=f2nd,系统低频区间段的共振频率点减少1个。第3阶模态频率f3rd和第4阶模态频率f4th在交点2处重合,因此kab=0.91时系统高频区间段内的共振频率点减少1个。第2阶模态频率f2nd和第3阶模态频率f3rd在交点3处相交在交点4处分离,因此当kab取值在(1.04,1.16)区间时系统中频区间段内的共振频率点减少1个。在交点2(kab=0.91)和交点3(kab=1.04)处,系统仅有2个模态频率,因此系统共振点减少2个。交点3处的低阶频率f1st值更大,对于改善系统低频扭振更有效。

表2 EMT扭转振动模态频率曲线交点坐标

图6 扭转振动模态频率fe随杠杆系数kab的变化曲线
同理,由图6(b)可知,EVT2模式中,随着kab增大,第1阶模态频率f1st和第2阶模态频率f2nd在交点1处重合,在交点4处分离。第3阶模态频率f3rd和第4阶模态频率f4th在交点2处重合。交点3处f1st=f2nd=f3rd。在交点2(kab=0.914)和交点3(kab=1.26)处,系统仅有2个模态频率,因此系统共振点减少2个,且交点3处的低阶频率f1st值更大,对于改善系统低频扭振更有效。
综上分析,选择交点3处的kab值可显著改变系统振动特性。为量化主从控制方法(M-SAC)的扭转振动抑制效果,对系统进行数值分析,同时设计了基于模态空间的最优控制方法(IMSOC)[17],进行仿真对比。
3.3 独立模态空间控制
对式(4)系统方程作线性变换,令Q=0。求得系统各阶固有频率fi及振型Φi。代入系统振型矩阵对x=[θe,θc1,θma,θg,θmb,θl]T作变换。

带入系统方程得

上式等号两边同时右乘ΦT,可得

式中:Mp为主质量矩阵;Kp为主刚度矩阵;为正交归一化矩阵;=I,为单位阵;=diag(ω1,…,ω1)为谱矩阵;q为6维模态坐标矢量;f=为6维模态控制矢量。ωi为第i阶模态固有频率。
将上式转换为关于模态空间状态矢量z的解耦状态方程

可按照模态阶数进行矩阵分块处理,其中:
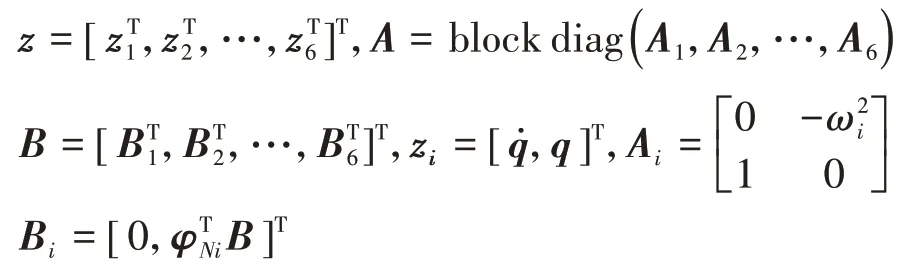
输出观测方程为
式中:C1和C2分别为对速度和位移的输出观测矩阵;C=[C1ΦN,C2ΦNω]T,ω=diag(ω1,ω2,…,ω6),Ci为系统第i阶模态的观测矩阵。
对第i阶独立模态进行线性反馈控制,可得系统第i阶的模态方程为

式中fi为第i阶模态控制力。当fi=(t,q˙i,qi)时,模态控制即为独立模态空间控制(IMSC)。选取线性比例控制,即

将式(14)代入式(15),可以得到

确定实际控制力u由式(11)可知:

式中为6×2阶模态控制矩阵。由于作动器数目小于所控制的模态数,故Bˉ不是方阵,不能利用u=求得u。因此采用伪逆法,即

综上可得独立模态控制方法的控制框图,如图7所示。
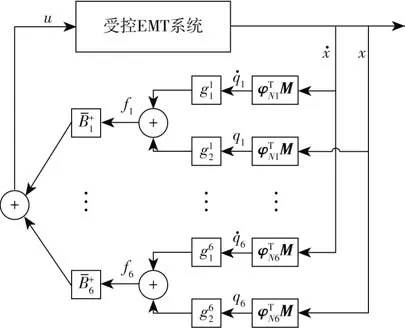
图7 独立模态空间控制框图
4 EMT系统扭转振动仿真分析
作为对比,IMSOC取i=1,2,即对系统第1阶和第2阶扭转振动模态进行最优控制。
M-SAC控制仿真参数设置为kp=30,ki=300,kd=1500,kab_EVT1=1.042,kab_EVT2=1.26。主从电机主动控制和最优模态空间控制方法的控制目标为降低低频共振峰值。发动机转矩脉动激励作用下,EMT各独立自由度的转速波动幅频特性如图8~图13所示。其中,扭振控制的目标区域已用灰色标出。
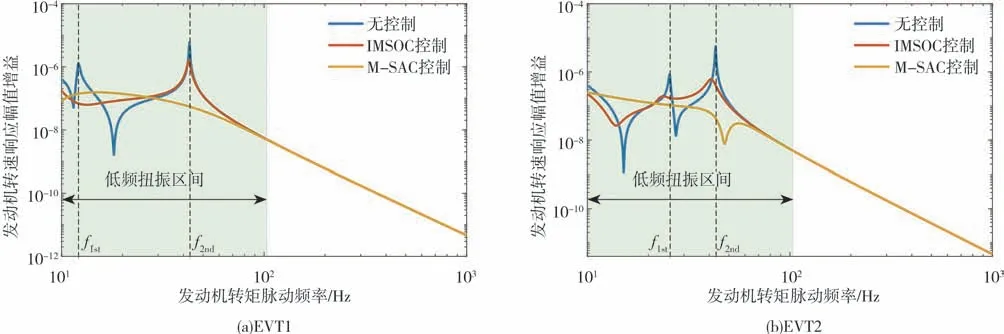
图8 发动机转速波动幅值频率响应特性
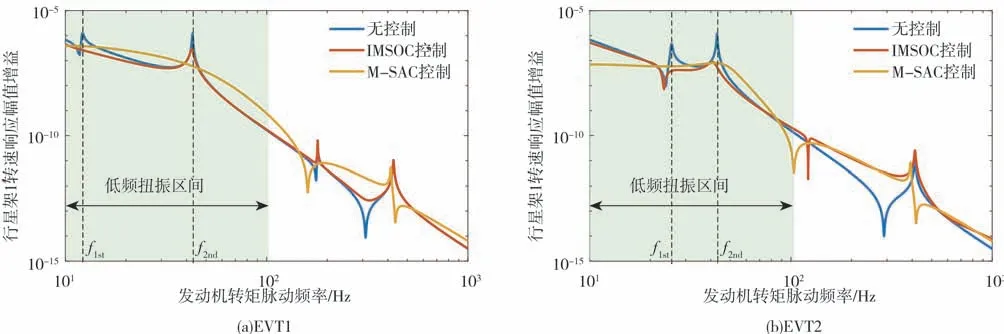
图9 行星架1转速波动幅值频率响应特性
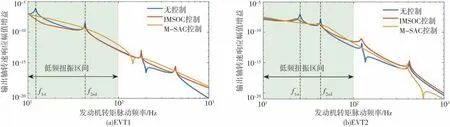
图13 输出轴端转速波动幅值频率响应特性

图10 电机A转速波动幅值频率响应特性
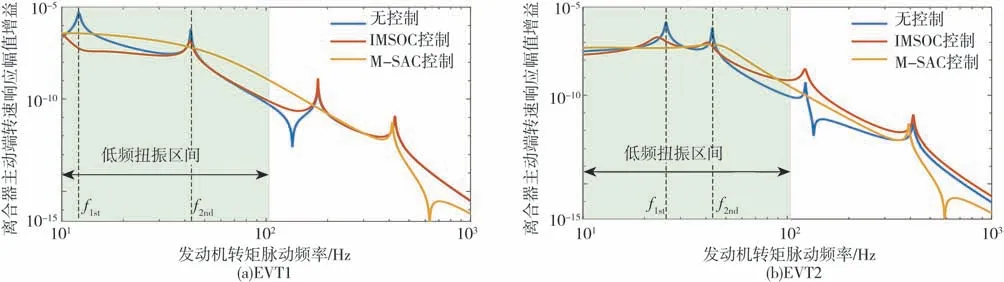
图11 离合器主动端转速波动幅值频率响应特性
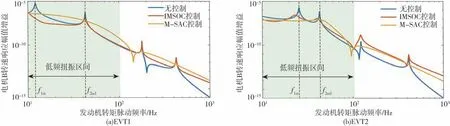
图12 电机B转速波动幅值频率响应特性
由图8~图13可知,在EVT1和EVT2两种模式下,EMT系统均含有4阶固有扭振模态,各阶模态频率与表1对应,其中,发动机转矩脉动激励的低频区域内,第1阶和第2阶模态扭振峰值极大,是恶化系统NVH性能的主要因素。
与未施加控制的EMT相比,IMSOC算法只对被控模态(第1阶和第2阶)有抑制效果,表现为既衰减响应幅值,也减小共振频率,使第1阶和第2阶模态对应的振动峰值明显抑制。对于未被控制的第3阶和第4阶模态频率区间,系统振动响应略有增大。
与未施加控制的EMT相比,主从控制算法(MSAC)减少了2个共振点,使100 Hz以内的低频带内幅值衰减很平滑。没有出现明显的峰值点。对于EMT系统低频扭振削峰效果很好。
主从控制算法(M-SAC)和最优模态控制算法(IMSOC)相比,前者削峰效果更好,具有很大的应用潜力。
5 结论
本文中通过对EMT系统的扭振特性及控制分析,得到如下结论。
(1)低频区域内,EMT系统含有4阶固有扭振模态,对系统NVH性能影响较大,其中,第1阶和第2阶扭振模态是主导因素。
(2)电机控制参数和系统扭振特性具有耦合关系,主从控制的杠杆比kab影响各模态频率的大小。
(3)采用串级控制方法能使稳态驱动转矩分配控制和扭振控制动态力矩的解耦,达到动力协调和扭振抑制的控制目标。
(4)主从电机控制算法可以减少系统扭振固有频率个数,有效衰减扭振响应峰值,改善EMT系统的动力学品质。

