整体液压顶升装置提升吊耳受力计算与优化

周任伟，李琴，吴思够，杨芳，范如谷

整体液压顶升装置提升吊耳受力计算与优化

周任伟1,2，李琴1，吴思够2，杨芳2，范如谷2

（1.西南石油大学 机电工程学院，四川 成都 610500；2.中国水利水电夹江水工机械有限公司，四川 乐山 614100）

提升吊耳是整体液压顶升装置中的关键受力结构，采用有限元静力学方法对其进行受力计算，得到各零部件及焊缝处的应力分布，由强度结果可知：富裕度较大，需进行结构优化设计。首先对提升吊耳进行敏感度分析，筛选出对目标结果影响较大的设计变量，进一步完成响应面分析，生成Kriging类型的响应面，最后采用MOGA（多目标遗传算法）迭代计算后寻得最优设计点。按照优化后的设计变量更新计算模型，并完成有限元静力学计算，得到各零部件及焊缝的等效应力分布，分析后得出：优化后的计算模型强度满足标准要求，且质量降低约41.7%，优化效果显著。

提升吊耳；强度；有限元；敏感度；响应面

如图1所示，整体液压顶升装置主要由顶升油缸、顶升支架、传力杆、底座等组成。基本原理为：顶升装置由单个液压顶升油缸驱动，通过4组传力杆与顶升支架立柱上的提升吊耳通过销轴连接，随着顶升油缸的伸缩，通过传力杆驱动顶升支架上下移动，实现整个装置的顶升功能。由于提升吊耳安装在顶升油缸下方，传力杆呈“伞”状布置，表现为顶升支架通过传力杆被提升的效果。顶升支架为模块化产品，可以通过布置不同数量的顶升支架以满足不同的顶升高度。

1.顶升油缸；2.传力杆；3.顶升支架；4.底座；5.立柱；6.斜杆；7.横杆。

顶升支架是装置中的核心承载结构，由4组立柱、4组斜杆、8组横杆组成，均为模块化零部件。立柱主要由薄壁矩形或圆形钢管和焊接在其表面的提升吊耳等零部件组成，为主要受力构件，其上的提升吊耳起着关键的传力作用，是关乎整个系统安全性、功能性的关键零部件之一。提升吊耳的强度计算对象不仅是吊耳本体，还应考虑到焊接位置的钢管、加强贴板及焊缝的强度等。

由于传统的力学公式对于这种复杂的焊接组合结构难以进行准确的受力计算，因此采用有限元软件完成对提升吊耳处焊接组合结构的静力学计算，得到各个零部件及焊缝的等效应力。采用有限元计算时，需要对模型进行简化处理，简化立柱结构中的连接法兰、连接板等，保留由钢管、加强贴板、提升吊耳及焊缝组成的计算模型，其中加强贴板的作用为增加钢管的局部刚度和强度，提高局部稳定性，从而保证整个装置的稳定性。如图2所示。

1.连接法兰；2.连接板；3.加强贴板；4.提升吊耳；5.钢管。

1 载荷计算

结合整体液压顶升装置的基本工作原理及设计参数，提升吊耳的受力主要发生在整个装置的顶升作业过程中，在此状态下，传力杆的轴向载荷直接作用在提升吊耳的吊耳孔壁，最终由提升吊耳将载荷传递到加强贴板与钢管上。根据整体液压顶升装置的总体布置，传力杆作用在提升吊耳的载荷与立柱的轴线方向呈30°角，按照直角坐标系进行受力分解，得到1和2，由于整体液压顶升装置的设计顶升载荷参数为竖直方向，即2的载荷值为已知参数，容易计算得到、1的载荷值。如图3所示。

图3 提升吊耳受力示意

整体液压顶升装置的额定顶升重量为25 t，每个顶升支架需承受25 t的竖直方向载荷，由4个立柱同时承受，平均分配载荷，单个立柱承受的载荷2＝62.5 kN，计算得1＝36 kN，＝72 kN，其中，重力加速度取＝10 m/s2。

2 初始值下的有限元静力学计算

有限元静力学分析的一般流程为：三维建模、模型处理、网格划分、载荷加载、约束处理、计算分析。有限元分析的原理是将连续的结构离散为有限个单元，推导出单元刚度矩阵，将单元矩阵组装形成结构总体刚度矩阵，求解方程，获得各单元节点的位移，由节点位移计算单元应变，最后计算得单元应力。随着计算机技术的发展，整个有限元分析过程可在有限元软件中完成。静力学分析的总体刚度矩阵为：

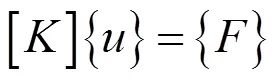
式中：[]为总体刚度矩阵；{}为结构的整体节点位移向量；{}为总体节点载荷向量。

2.1 有限元模型处理与网格划分

对于提升吊耳的计算，按照表1中的初始值建立1:1的三维实体模型，并将焊缝以实体的形式反映在模型上。

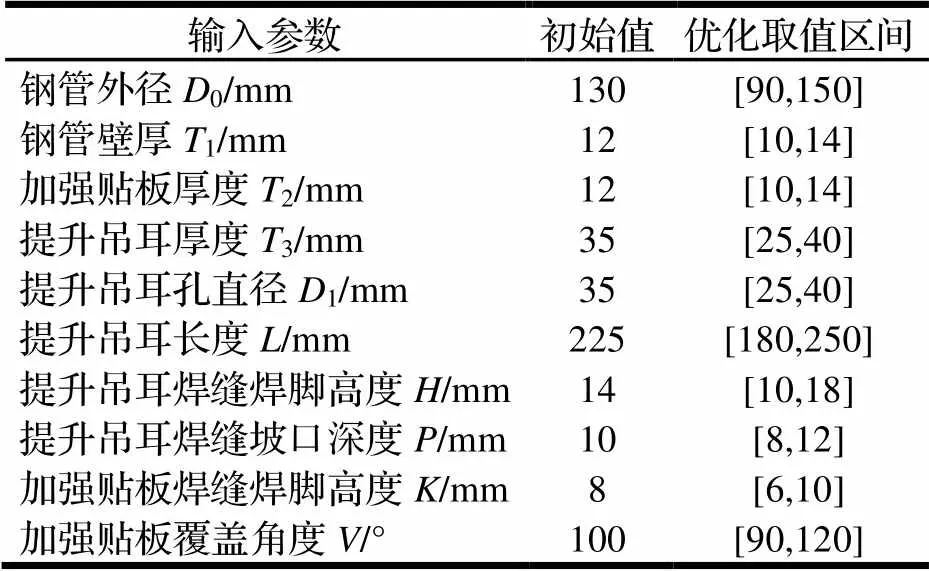
表1 提升吊耳的设计变量统计

将实体模型导入有限元软件，完成材料属性设置、模型处理等流程，确定材料为各向同性的Q355B低合金钢，密度7.85×103kg/m3，弹性模量210 GPa，泊松比0.3，屈服强度355 MPa，抗拉强度470～630 MPa。进行网格划分时，在应力集中位置和特别关心部位的局部进行了必要细化[5]，先按照软件的默认设置使用自动网格划分功能，完成初步网格的划分[7]，为确保计算结果的精度，将总体网格尺寸设置为5 mm，并对吊耳孔、焊缝处的网格进行局部细化，尺寸设置为2 mm，再次进行网格划分，进行网格评估后确定网格质量满足计算要求，统计出单元数量147452、节点数量319881。网格划分如图4所示。

图4 提升吊耳网格划分示意

2.2 载荷加载与约束处理

载荷加载时，首先定义提升吊耳平面内平行焊缝长度的方向为轴、垂直焊缝长度的方向为轴，垂直提升吊耳平面的方向为轴。将传力杆传递的载荷按照分量的形式分别加载到提升吊耳孔壁上，轴方向的载荷分量加载值为2＝75 kN，轴方向的载荷分量加载值为1＝43.3 kN，由于轴方向不承受任何载荷，所以加载值为0。传力杆与提升吊耳之间为销轴连接，在有限元软件中采用轴承力加载的方式模拟销轴与吊耳孔的接触方式，这样可以最大程度地还原真实受力情况，保证吊耳孔壁的应力分布准确性。

约束处理时，结合顶升作业实际情况对计算模型中钢管顶部截面和底部截面施加约束。顶部截面采用固定约束；底部截面采用位移约束，并释放钢管轴向的位移约束，同时约束其余方向位移。提升吊耳与加强贴板间不直接设置接触关系，而是分别与二者之间的焊缝建立绑定的接触关系，采用焊缝进行载荷传递，加强贴板与钢管之间采用同样的处理方式，该处理方式可以真实模拟不同零件之间的连接关系，同时可以准确反应焊缝的应力分布。

2.3 计算分析

钢结构设计标准[1]中对Q355B钢材的抗拉强度设计值及角焊缝的抗拉、抗压和抗剪强度设计值均有明确的要求。零部件及焊缝强度设计值如表2所示。

表2 零部件及焊缝强度设计值

计算模型质量为29.01 kg时的计算结果如表3所示。有限元静力学计算结果如图5所示。

表3 模型的计算结果

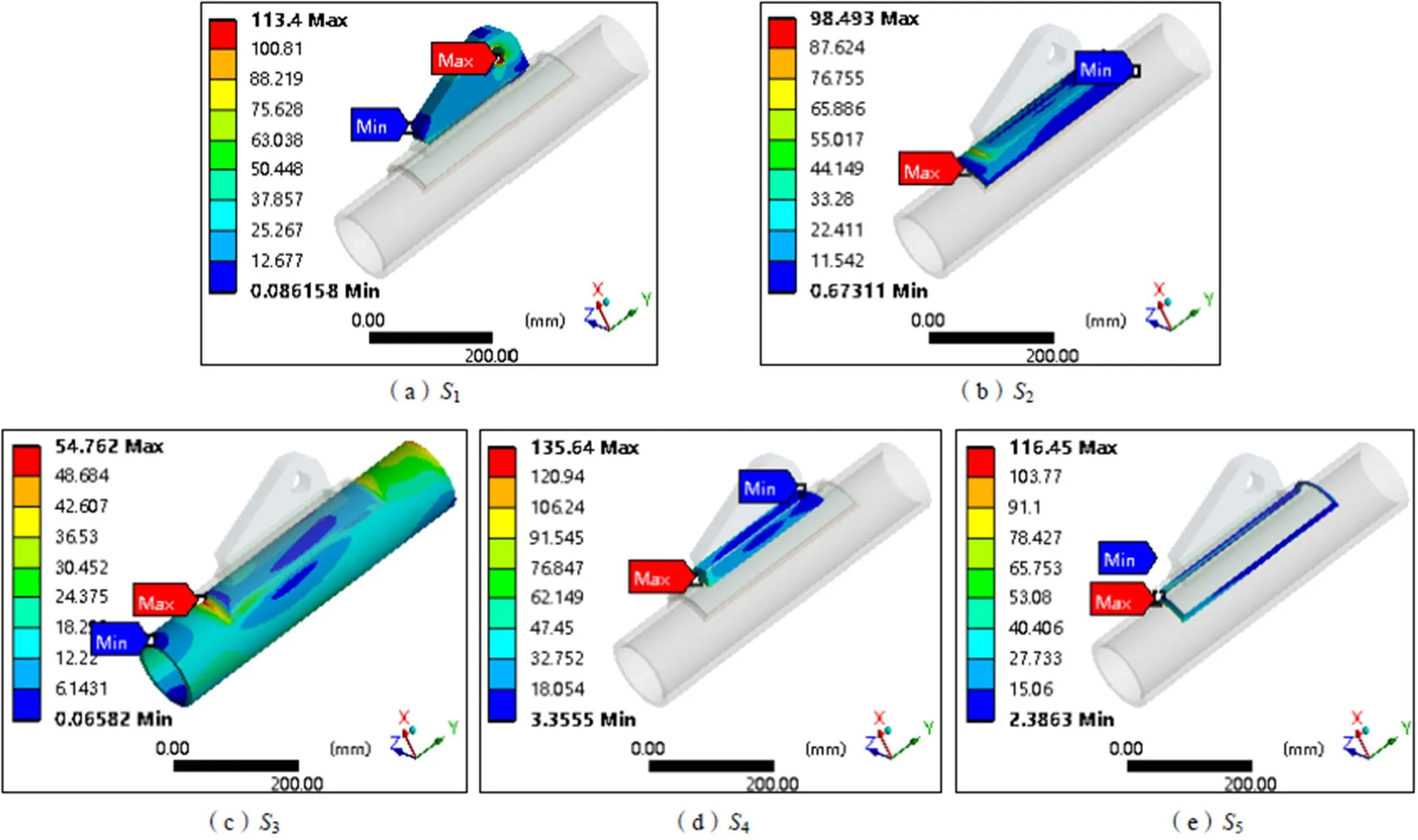
图5 有限元静力学计算结果云图

计算模型中钢结构部分最大等效应力位于提升吊耳孔壁，焊缝部分最大等效应力位于提升吊耳焊缝，均未超过强度设计值，且存在较大的裕度。同时，由于顶升支架及立柱为模块化产品，数量多，进行提升吊耳的结构优化设计时，需兼具良好的必要性和经济性。优化分析前需要进行灵敏度分析，在大量的输入参数中筛选出对输出参数影响较大的作为优化设计的设计变量，从而达到减小设计变量数量、降低优化设计计算量的目的。

3 敏感度分析

敏感度分析是指，模型有若干个输入参数，令每个输入参数在优化取值区间内变动，研究和预测这些变动对模型输出参数的影响程度，可以理解为，是分析输入参数对输出参数的重要性[2,9]。由于初始值下的静力学分析结果得出整个结构最大应力发生在提升吊耳焊缝处，因此在提升吊耳的参数敏感度分析中将主要的设计变量作为输入参数、各零部件及焊缝的等效应力和计算模型的质量作为输出参数，按照表1确定各设计变量的初始值、取值区间，通过软件自动生成100组设计点，采用Spearman相关性分析方法，完成敏感度分析，得到各输入参数对输出参数的敏感度分析结果，如图6和表4所示。

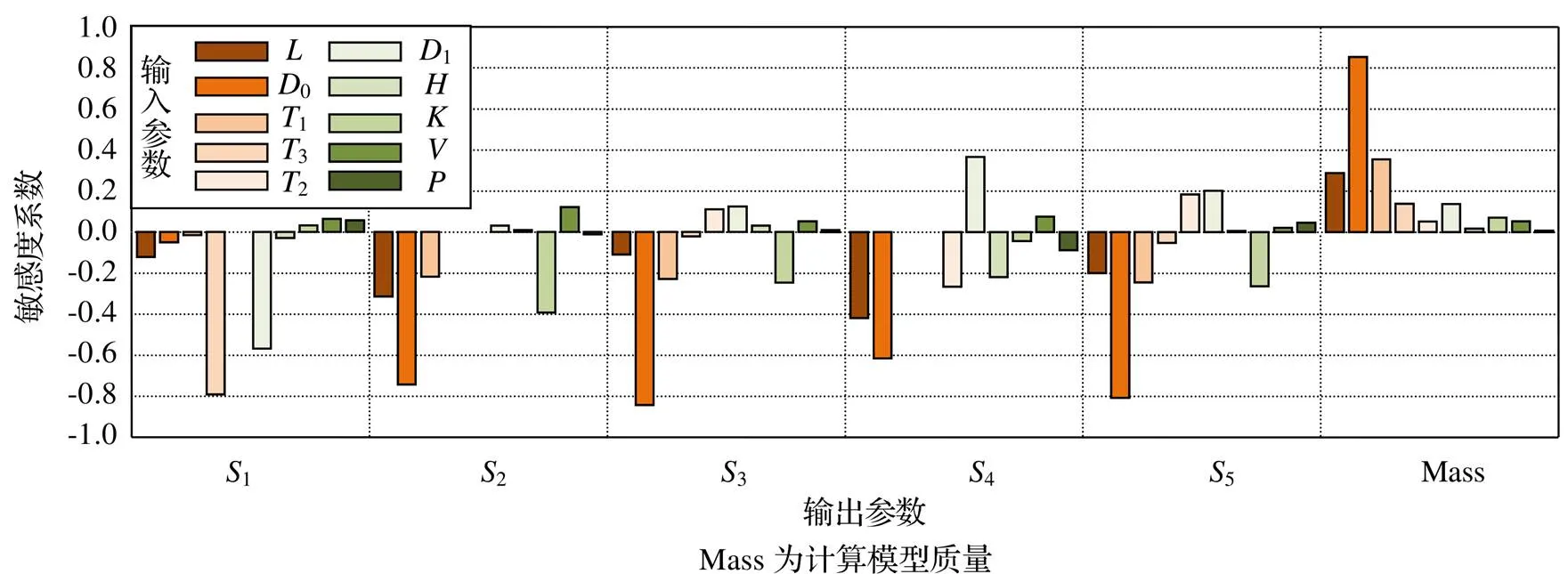
图6 敏感度分析结果

表4 敏感度系数统计表

由图6和表4可知，各输入参数对输出参数的影响不同，且存在部分输入参数的敏感度系数为负，说明该输入参数与输出参数为负相关。根据输入参数对输出参数的影响程度，去除敏感度系数较小的输入参数后，筛选出0、1、、3、1、、2、，共8个输入参数作为响应面优化设计的设计变量。

4 基于响应面的结构优化设计

结构优化设计是指在给定约束条件（强度、刚度等）下，按某种目标（如重量最轻、成本最低等）求出最好的设计方案。其基本思想是寻求目标函数的下降方向，然后在下降方向中寻优，最终获得符合要求的最优解[9]。结构优化设计的基本要素为：设计变量、目标函数、约束条件。常用的数学模型为[2]：

提升吊耳的优化设计中，将筛选后的设计变量作为连续设计变量，并按照表1确定各设计变量的初始值和优化取值区间，各个零部件及焊缝等效应力的最大值不大于表2作为约束条件，计算模型的质量最小作为目标函数。采用基于响应面的结构优化技术，首先完成响应面分析并得到响应面结果，再按照寻优算法在响应面上找到目标点，最后将优化后的设计变量反馈到计算模型并进行有限元计算，得到应力云图，完成结果评估。

4.1 响应面分析

响应面分析是利用合理的试验设计方法并通过实验得到一定数据，采用多元二次回归方程来拟合因素与响应值之间的函数关系。可以进行响应面分析的抽样方法有多种，常用的包括PB（Plackett-Burman Design，筛选试验设计）、CCD（Central Composite Design，中心复合试验设计）、BBD（Box-Behnken Design，中心组合设计）等[2]。由于各个设计变量的输入设计点有限，所以通过有限的设计点拟合响应面进行研究，可以在保证准确性的同时有效减少计算工作量。

在提升吊耳的响应面分析中，将筛选后的设计变量作为输入参数，各零部件的最大等效应力、计算模型的质量作为输出变量，通过CCD抽样方法获取了81个设计点，同时插入5个验证点确保拟合函数的准确性和精度，最终生成Kriging类型的响应面。如图7所示。

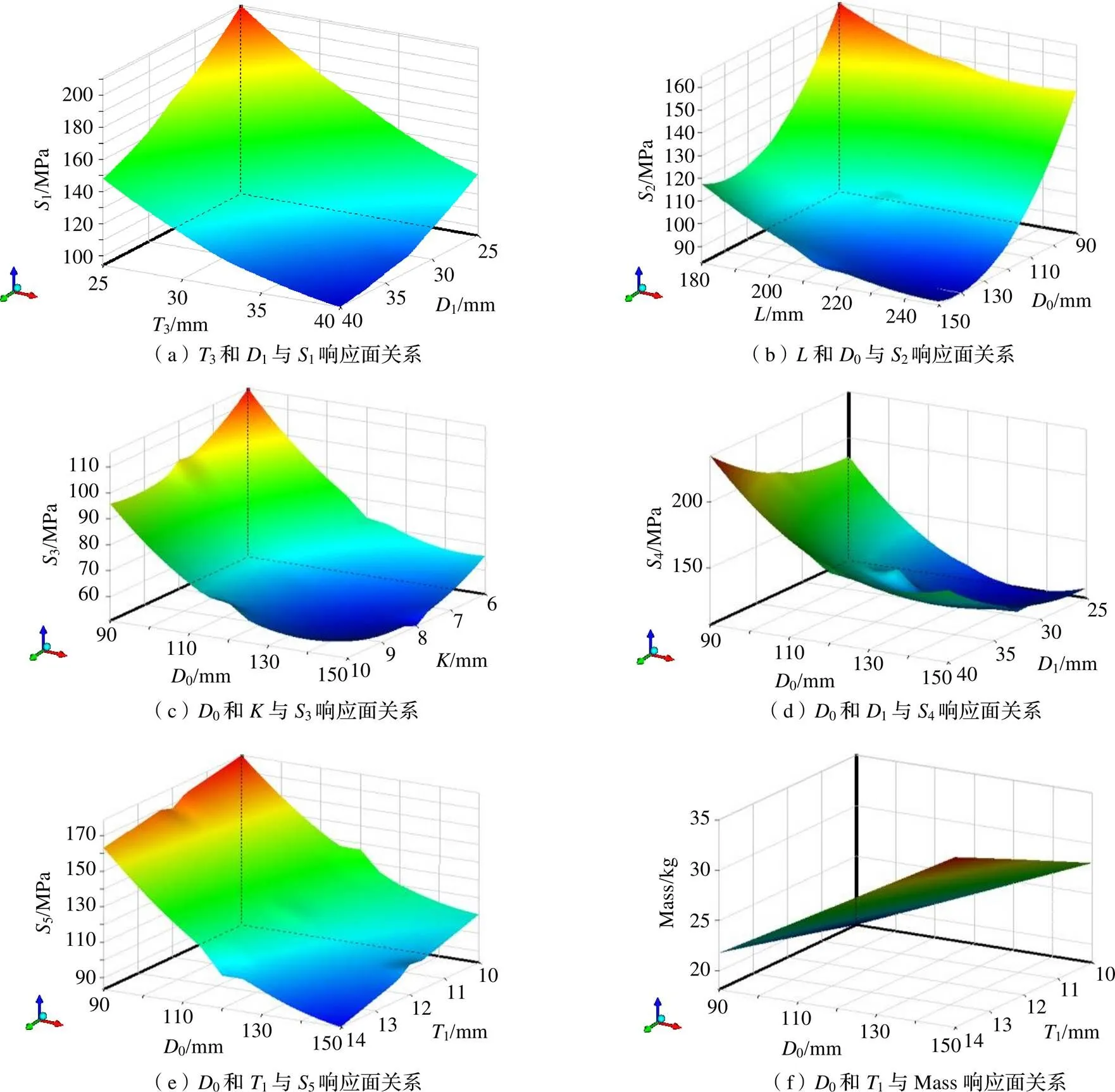
图7 响应面分析结果示意

由图7可知，0和1等设计变量对计算模型质量基本符合线性关系且为正相关，0、1、、1、等设计变量对各零部件及焊缝等效应力呈非线性关系，既存在正相关，也存在负相关。各输入参数对输出参数的影响与敏感度分析结果基本一致。

4.2 响应面优化设计

响应面优化方法可同时对多个目标进行优化，从给出的样本中得出最佳设计点，可制定不同的优化目标用于优化设计[9]。结合敏感度分析和响应面分析的结果进行结构优化，采用MOGA（Multi-Objective Genetic Algorithm，多目标遗传算法）在响应面上搜寻出既满足约束条件又达到计算模型质量最小的设计点。经过19次计算，得到3组优化解，由于设计变量为连续变量，优化后的设计参数出现小数值，实际生产存在困难，结合钢板及管材的尺寸参数，对优化后的结果进行适当调整。如表5所示。

5 优化后的有限元静力学计算

将优化后设计变量的调整值传递给计算模型，驱动计算模型完成尺寸调整，生成优化后的计算模型，并对该计算模型进行有限元静力学计算，得到计算结果云图，如图8所示。

优化后模型的计算结果如表6所示，计算模型质量为16.9 kg。可以判断：各零部件及焊缝等效应力的最大值均未超过强度设计值，满足要求。与初始值状态下计算模型质量相比，优化后的质量降低约41.74%，优化效果明显。

表5 优化后设计参数统计

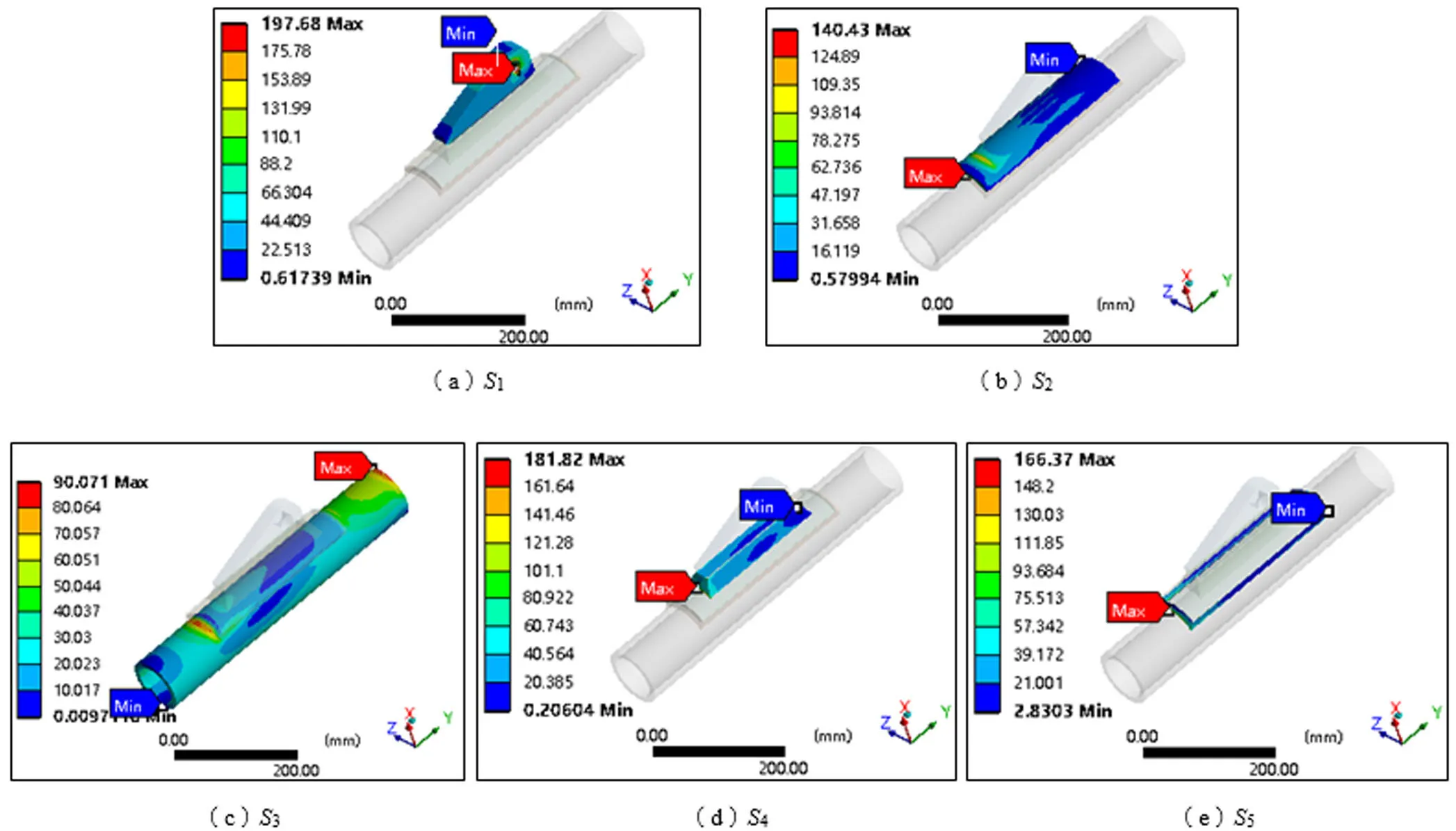
图8 优化后的有限元静力学计算结果云图

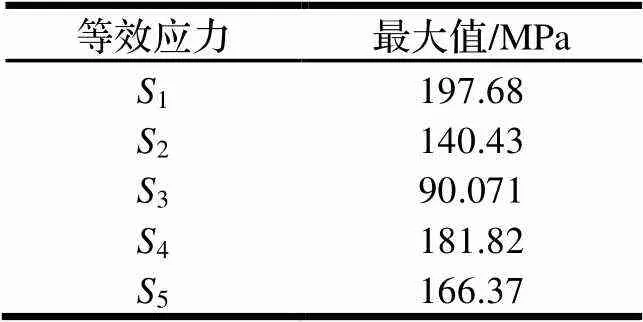
表6 优化后模型的计算结果

6 结论

采用有限元静力学计算完成了初始值下提升吊耳计算模型的计算分析，得到了满足标准要求的结论，由于强度具有较大的裕度，可进行结构优化。进一步对提升吊耳进行敏感度分析，筛选出8个设计变量用于优化设计，通过CCD抽样方法获取了81个设计点，得到Kriging类型的响应面，采用多目标遗传算法（MOGA）在响应面上经过19次迭代后，搜寻得到3组既满足约束条件又达到计算模型质量最小的设计点，并结合实际生产情况，对优化后的设计参数进行调整，最后对优化后的计算模型进行有限元静力学计算，结果满足强度设计要求，质量由29.01 kg降低为16.9 kg，优化率41.74%，效果明显，对于数量多且模块化的顶升支架，显著降低了原材料成本，具有良好的经济性。

[1]中华人民共和国住房和城乡建设部，中华人民共和国质量监督检验检疫总局. 钢结构设计标准：GB 50017－2017[S]. 北京：中国建筑工业出版社，2017.

[2]白新理. 结构优化设计[M]. 郑州：黄河水利出版社，2008.

[3]王贵强，邵伟平，邹显楠，等. S型折叠悬臂梁应力仿真分析[J]. 机械，2020，47（8）：1-5.

[4]朱渭定. 起重机耳孔拉板的计算[J]. 水利电力施工机械，1982，（2）：18-15.

[5]李晨，曾京. 某B型地铁列车转向架强度分析[J]. 机械，2020，47（8）：31-36.

[6]程玉芹，王朝，刘昆. A形吊耳强度有限元分析[J]. 计算机辅助工程，2013（S2）：269-273.

[7]欧昭，胡真清，黄日恒. 基于ANSYS的主轴箱优化设计[J]. 机械，2019，46（12）：61-66.

[8]马晓燕. 基于ANSYS Workbench的联轴器膜片响应面优化[J]. 拖拉机与农用运输车，2015（6）：47-50.

[9]刘承杰，罗鹏，赵磊，等. 基于ANSYS Workbench曲柄销轴的优化设计[J]. 应用力学学报，2017，34（6）：1140-1144.

[10]王雅俊，王有志，张向阳，等. 基于有限元法的板式吊耳安全分析[J]. 人民黄河，2018（7）：117-120.

Force Calculation and Optimization for Lifting lugs of Hydraulic Jacking Device

ZHOU Renwei1,2，LI Qin1，WU Sigou2，YANG Fang2，FAN Rugu2

( 1.School of Mechanical Engineering, Southwest Petroleum University, Chengdu610500, China;2.Sinohydro Jiajiang Hydraulic Machinery Co., Ltd., Leshan 614100, China )

The lifting lug is the key stress structure in the integral hydraulic jacking device. In this paper, the finite element static method is used to calculate the stress distribution of each component and welding seam. The strength result shows that the margin is relatively large, thus and the structure needs to be optimized. First, the sensitivity analysis of the lifting lugs is carried out to screen out the design variables that have a greater impact on the target results, and then the response surface analysis is completed to generate the response surface of Kriging type. Finally, MOGA ( Multi-Objective Genetic Aalgorithm ) iterative calculation is adopted to find the optimal design point. After updating the calculation model according to the optimized design variables and completing the finite element static calculation, the equivalent stress distribution of each component and welding seam is obtained. The analysis result indicates that the strength of the optimized calculation model meets the standard requirements, and the mass is reduced by about 41.7%, which turns out to be a great optimization.

lifting lug；strength；finite element；sensitivity；response surface

TH122；TH123；TH69

A

10.3969/j.issn.1006-0316.2021.09.005

1006-0316 (2021) 09-0028-08

2020-12-14

周任伟（1990－），男，四川井研人，硕士研究生，工程师，主要研究方向为机械工程、机械设计，E-mail：657846260@qq.com；李琴（1970－），女，四川乐山人，硕士，副教授，主要研究方向为油气装备现代化设计与关键技术等；吴思够（1973－），男，四川夹江人，教授级高级工程师，主要从事水电站启闭设备的设计与研究；杨芳（1972－），女，贵州凯里人，教授级高级工程师，主要从事水电站启闭设备的设计与研究；范如谷（1982－），男，四川成都人，高级工程师，主要从事水电站启闭设备的设计与研究。