年龄等级结构捕食种群系统的可控性与镇定

何泽荣*,徐俊芳

(杭州电子科技大学 运筹与控制研究所，浙江杭州 310018)

§1 引言

为何研究种群系统的可控性? 主要动机包括两方面:一是保护生物多样性,拯救濒危物种,使种群朝着人们期望的方向演化;二是获得有趣也有挑战性的数学控制问题,拓展无穷维系统控制理论疆界.对于具有年龄或者个体尺度结构的种群系统模型的可控性,已有一些研究成果面世,参见文[1-9]及其所引文献.这些成果深化人们的认知,也是进一步发展的基石.另一方面,种群镇定问题也很值得探讨,因为种群状态的巨幅振荡通常都是不祥之兆,容易导致种群消亡.现有镇定性成果可参见[10-16].

通观具有个体结构差异(如年龄,尺度,空间位置)的种群系统模型,其现有可控性成果都是基于常规的年龄(尺度,空间)结构模型,并不能反应个体的等级(或称社会地位)差异,而这种差异既是普遍的,也是重要的;生态学方面参见综述文献[17],基于数学模型的演化分析可见[18-28],可控性成果罕见.有鉴于此,本文探讨一类基于个体年龄等级差异的捕食种群系统的可控性和零解镇定问题.与常规年龄结构模型比较,本文的主要特点是采用二元函数描述种群内部环境,而不是通常只依赖于时间的一元函数.相应的模型更逼近实际,且理论分析的难度更大. §2提出模型后, §3运用多值映射的不动点方法建立系统可控性, §4构造适当的最优控制问题,由此确定如何选择控制策略,实现系统可控性. §5, §6分别处理零解镇定问题,总结全文.

§2 系统模型

假定种群中的个体具有基于年龄的等级差异,密度制约和种间相互影响均由相应种群的内部环境决定.运用连续年龄结构生灭系统的标准建模方法,可得下列动态模型:

其中Q=(0,A)×(0,T),A代表个体最大年龄,T为系统演化时长.p1(a,t)和p2(a,t)分别表示食饵和捕食者种群的瞬时年龄密度.E(pi)(a,t)表征第i种群的内部环境,α为等级折扣系数.µi(a)与mi(E(pi)(a,t))分别给出自然死亡率与内部竞争导致的额外死亡率.f1(E(p2)(a,t))描述因捕食产生的食饵死亡率,f2(E(p1)(a,t))则表示食饵对捕食者的增长贡献.βi(a,E(pi)(a,t))为个体平均繁殖率,(a)是初始年龄分布.控制函数ui(a,t)表征迁进或移出.

为了后续理论分析所需,提出下列假设:

§3 近似可控性

定义3.1若对任意初始分布

则称系统(1)在[0,T]上近似可控.

记p(0,0)为系统(1)相应于u=(0,0)的解.不失一般性,可假设‖p(0,0)(·,T)−‖>1.

将函数mi,fi,βi中的内部环境E(p)=(E(p1),E(p2))固定为P=(P1,P2),系统(1)退化成

易知系统(2)可以视为两个独立的子系统,根据文献[5]中的结果可知子系统均可控;亦即,存在ui ∈L∞(Q)使得

下文以此为基础,运用多值映射的不动点方法,将系统(2)的可控性拓展到系统(1).为此,需要先对线性系统(2)做一些分析.

约定记号

引理3.1对任意给定的P=(P1,P2)∈(L∞(Q))2,及任意u=(u1,u2)∈U,系统(2)的解pu(·,·;P)=(·,·;P))满足

其中E(p)t和E(p)a分别表示关于t和a的偏导数,常数C1独立于P,u.

证由(2)和特征线方法可得

其中函数Fi,Ki定义如下:

下文只分析T >A的情况.相反的情形可以类似处理.

据函数关系式(7)-(8)和(10)-(11),利用本文基本假设易知

Πi(a,t,s;P)≤1,即使M2(a,t;P)能取负值,它也有下界,从而函数Π2仍有上界;

结合(9)与上述估计,可知存在独立于P,u的常数C2使得0≤buii(t;P)≤C2.从而表达式(5)和环境E(pi)的定义保证了与的一致有界性.

下列引理是已知的(见[29,p452]).

引理3.4(Ky Fan-Glicksberg)如果以下条件成立:

(1) 集K为局部凸空间X中的非空紧凸集;

(2) 集值映射G:K →2K上半连续;

(3) 对任一x ∈K,G(x) 是非空闭凸集,

那么G至少有一个不动点.

定理3.1系统(1)在空间(L∞(Q))2中近似可控.

证令X=(L∞(Q))2,集K由引理3.2给出.定义多值映射G:K →2X如下:若P ∈K,则

引理3.1 意味着:对任一P ∈K,G(P)∈2K.

容易看出K是凸集.引理3.2表明:引理3.4中的条件(1)满足.

根据文[5]中的可控性结果知:G(P)/=∅.由于控制变量u=(u1,u2)属于线性系统(2)的非齐次项,故G(P)必为凸集.此外,引理3.3保证了集G(P)的闭性.所以,引理3.4中的条件(3)也成立.

只需再证G的上半连续性.

进一步,关系E(pun)∈G(Pn)和(3)式意味着控制函数un必须满足

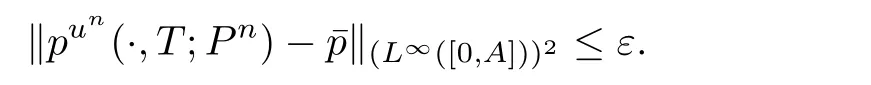
对上列不等式取极限,即得

因此,h=E(p(·,·;P))且h ∈G(P).

总之,映射G满足引理3.4的所有条件,它存在不动点.这意味着系统(1)近似可控.

§4 确定控制策略

定理3.1表明:存在控制函数向量u=(u1,u2)∈U,使得系统(1)在T时刻相应的状态与预先给定的目标任意接近.一般而言,有许多(甚至无穷多)这样的控制向量.应该如何选择呢?

由于实施任何控制都需要成本,自然希望以最小成本完成种群状态调节.因此,如果下列最优控制问题存在唯一解,那么就将该解作为可控性所需的控制函数.

(P1) 寻求u∗=()∈U,使得J(u∗)≤J(u),∀u ∈U,其中

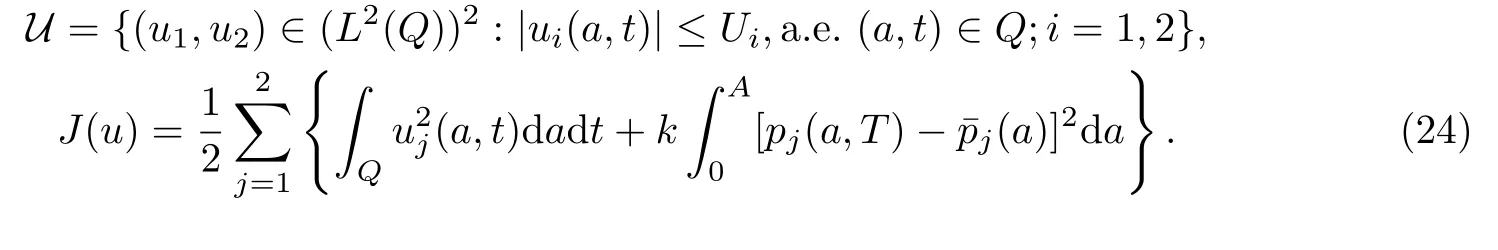
这里k为罚参数,(u,p)满足系统(1),为给定的目标状态.

应用类似于引理3.3的证明方法,可以证明下列结果(细节省去).

引理4.1系统(1)的解pu关于u连续.

不失一般性,下文假设m1(x)=m2(x)≡0.

定理4.1控制问题(P1)的任一最优解u∗=()都具有反馈结构=Fj(k|qj|),j=1,2,其中截断函数Fj定义为

共轭变量qj满足下列共轭系统

注意主方程中的变量(a,t)已被省去(出于简洁性考虑).

证令(u∗,p∗)为问题(P1)的最优对.对任一给定的切向量v ∈TU(u∗)(集U在u∗处的切锥),当ε充分小时必有u∗+εv ∈U.因而J(u∗)≤J(u∗+εv);此即

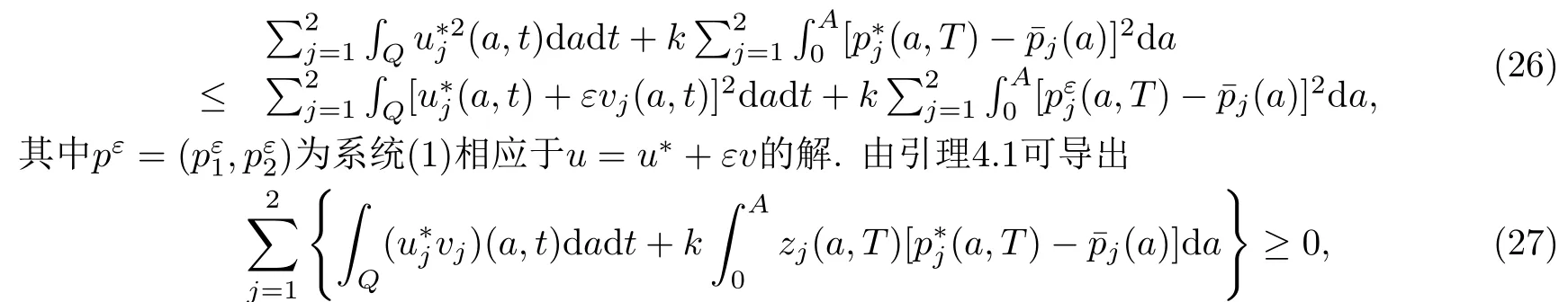
其中z(a,t)=(z1(a,t),z2(a,t)) :=limε→0+ε−1[pε(a,t)−p∗(a,t)]是下列系统的解.(略去主方程中的变量(a,t))

应当注意:对于给定的p∗=(),极限limε→0+ε−1[pε(a,t)−p∗(a,t)]的存在性和系统(28)的适定性可用标准方法处理[1].

将(28)的第i个方程乘以qi(a,t),并在区域Q上积分,可以导出(应用(25))

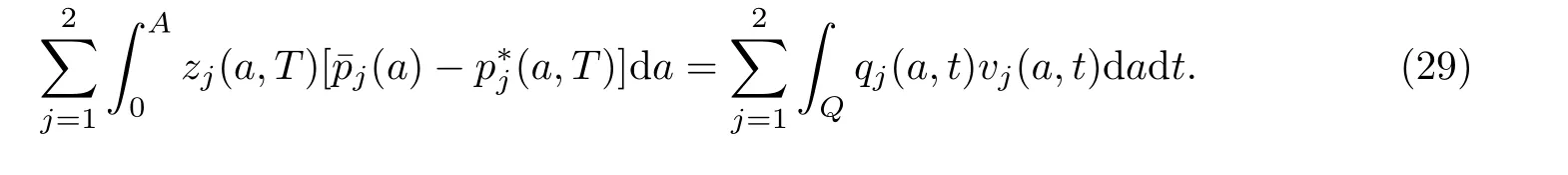
结合(29)与(27),可知下列不等式

对于任意v ∈TU(u∗)均成立.因此(kq12)∈NU(u∗)(集U在u∗处的法锥).应用法向量的结构特征即得定理结论.

下列结果建立控制问题(P1)最优解的存在唯一性.

定理4.2如果T足够小,那么最优控制问题(P1)有且只有一个解.

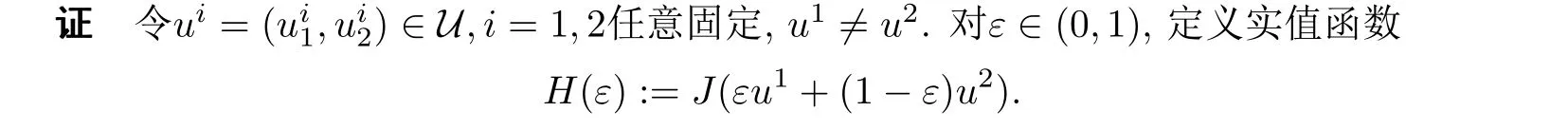
下文将证明H′(ε)严格单调增加.

分别记pε和pε+δ(δ >0充分小)为系统(1)相应于εu1+(1−ε)u2和(ε+δ)u1+[1−(ε+δ)]u2的解.那么

根据p和q的连续性及有界性(令其上界分别为C3和C4)可得

代(35)入(34),即可导出

当T充分小时,必有(ε1−ε2)H′(ε1)−H′(ε2)>0.因此,H(ε)严格下凸,存在唯一ε∗∈(0,1)最小化H(ε).从而,泛函J(u)有唯一最小元ε∗u1+(1−ε∗)u2.

§5 零解镇定

首先考察下列未受控系统零解的稳定性:

系统(37)在(0,0)处的线性化如下:

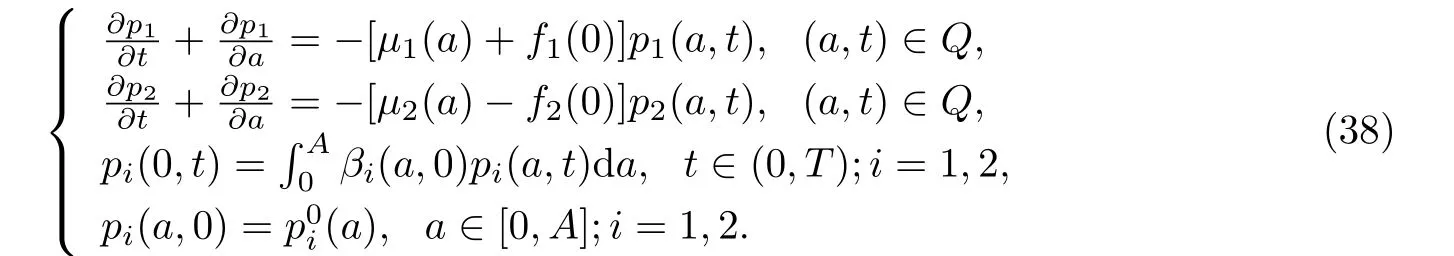
考虑系统(38)形如pi(a,t)=wi(a)exp{λt},i=1,2的解,可得

将(40)代入(38)的第三个等式,导出特征方程

将(41)左端视为实变量λ的函数,由其单调性易知:若存在i ∈{1,2}使得

则方程(41)至少有一个正实根,从而(37)的零解不稳定.

一个很自然的问题是:应当采取怎样的迁移策略才能迫使零解稳定? 在有限时域[0,T]上,此问题可作如下陈述.(P2) 寻求u∗∈U,使得J(u∗)≤J(u)对任意u ∈U均成立,这里

其中k代表罚参数,向量函数对((u1,u2),(p1,p2))满足下列受控系统约束:

运用类似于定理4.1的分析方法,可以给出问题(P2)中最优解的下列描述.

定理5.1问题(P2)有唯一解=F(qi),i=1,2,其中共轭向量(q1,q2)由下列共轭系统给出.(主方程中的变量(a,t)已略去)

函数F,,由(25)定义.

§6 结论

本文基本假设(A1)-(A6)的生态学意义明确,(A1)对自然死亡率的限制是与有限的最大年龄相呼应,数学方面的要求完全合理.定理3.1表明具有个体年龄等级差异的捕食种群系统是近似可控的;换言之,必定存在个体迁移策略(u1,u2)使得系统终态(p1(a,T),p2(a,T))任意接近预定目标.定理4.1和4.2显示这种策略可由(1),(25)以及定理4.1中的反馈控制率给出.共轭梯度法[30,p29]可用于迁移策略的近似计算.因此,关于此类种群系统调控的理论基础和计算方法均已具备.鉴于农林业害虫抑制,传染病和生物入侵防控的现实需求,定理5.1提出的零解镇定方法也是有价值的.

致谢：作者感谢审稿专家和编辑老师的宝贵意见.