一类具有胞内时滞和饱和CTL免疫反应的HTLV-I感染模型的全局动力学性态

张丽茹,徐 瑞*

(山西大学复杂系统研究所,山西太原 030006)

§1 引言

人类T细胞白血病或淋巴瘤病毒I型(HTLV-I)是一种在感染者中无限期存在的逆转录病毒,其感染力弱,并且几乎不出现在血浆中,通过感染细胞与未感染细胞的直接接触来传播病毒.HTLV-I感染者是终身无症状携带者,其中只有0.25%-3%的感染者会发展成HAM/TSP,2%-3%的感染者会发展为ATL,这些患者的外周血中CD8+毒性T淋巴细胞(CTL)的含量很高[1].实验证明一方面CTL可以降低病毒的载量及清除感染的细胞从而起到保护作用[2-3];但另一方面,CTL含量过高会释放大量的毒素导致出现HAM/TSP的症状,故通过调节CTL免疫反应水平可以有效防止HAM/TSP的发展[4].虽然到目前为止还没有治愈HTLV-I的方法及中和疫苗,对于HTLV-I相关疾病的发病机制也尚未清楚[5],但了解CTL 免疫反应对控制HTLV-I病毒感染具有重要意义.

近几十年来,对于HTLV-I感染动力学模型的研究引起了很多学者的关注[6-12].文献[6]考虑了如下具有CTL免疫反应的HTLV-I感染动力学模型:

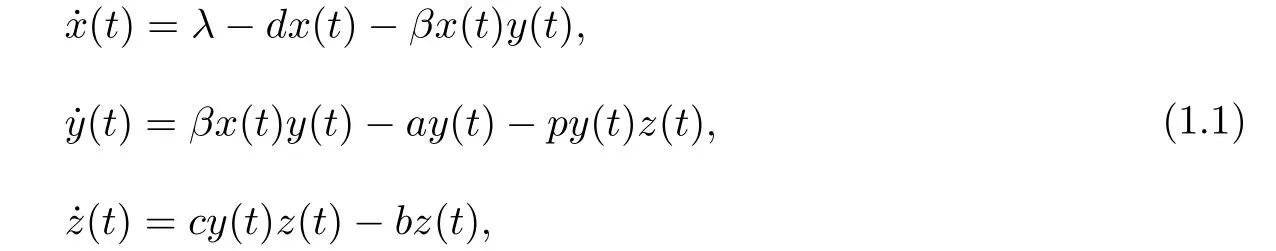
其中x(t),y(t),z(t)分别表示t时刻未感染的CD4+T细胞,感染的CD4+T细胞和CTL免疫细胞的浓度;λ表示未感染的CD4+T细胞的产生率;d,a,b分别表示未感染的CD4+T细胞,感染的CD4+T细胞和CTL免疫细胞的死亡率;βxy表示单位时间内新的感染细胞产生的速率;pyz表示通过CTL免疫反应清除感染细胞的速率,cyz表示CTL免疫细胞的生成速率,其参数值都是正值.

系统(1.1)假定感染过程遵循质量作用原理,即感染细胞与未感染细胞之间的感染率是一个常数.文献[7]通过实验说明寄生虫剂量与感染率之间的关系是非线性的.在文献[8]中,Song和Neumann指出病毒感染动力学模型中双线性感染率很难精确描述未感染细胞的感染过程,并提出非线性饱和感染率βxv/(1+αv)来代替质量作用感染率.

在实际情况下,HTLV-I是通过感染细胞与未感染细胞的直接接触来传播,但接触时不会立刻被感染,需要经过一段时间,因此在模型中考虑胞内时滞是很有必要的.Sun和Wei考虑了具有胞内时滞的HTLV-I感染模型[9]:

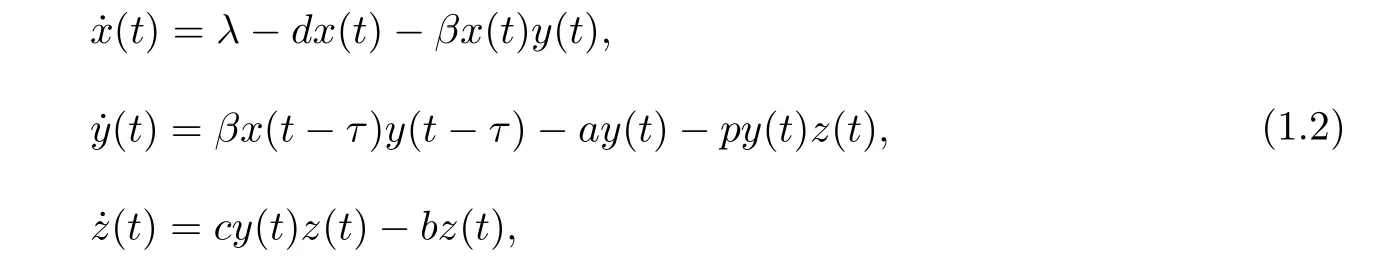
其中τ表示未感染细胞的被感染过程,其主要分为三个阶段.第一阶段是病毒进入未感染的CD4+T靶细胞后,首先病毒RNA在逆转录酶抑制剂的作用下逆转录成病毒DNA,然后病毒DNA 整合到宿主基因组之间的时期;第二阶段是进行病毒RNA转录和病毒蛋白的翻译的时期;第三阶段是病毒释放并成熟的时期[10].

模型(1.1)和(1.2)均假定CTL免疫细胞的生成速率与感染细胞的浓度成正比.事实上,当感染细胞的浓度达到一定量时,CTL免疫细胞的生成速率不再增加,免疫反应达到饱和状态.基于以上原因,文献[11]选取免疫反应函数为cy(t)z(t)/(z(t)+k),其中k刻画T细胞被抗原提呈细胞绑定和激活的趋势[12].

基于文献[6,9,11]的工作,本文研究胞内时滞和饱和CTL免疫反应对HTLV-I感染动力学的影响.为此考虑下列微分方程模型:

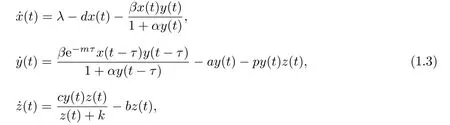
其中e−mτ是感染细胞从时刻t −τ到时刻t的存活率,其他参数的生物学意义与模型(1.1)相同.

系统(1.3)满足如下初始条件:

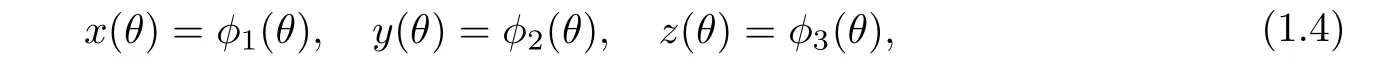
其中φi(θ)≥0,θ ∈[−τ,0),φi(0)>0,φi(θ)∈C([−τ,0]),这里={(x1,x2,x3) :xi ≥0,i=1,2,3}.由泛函微分方程的基本理论[13]可知系统(1.3)在初始条件(1.4)下的解是唯一的.

定理1.1系统(1.3)在初始条件(1.4)下的解非负且最终有界.

证 反证法.假设t1>0是第一个使得x(t)=0的时刻,则当00,由系统(1.3)的第一个方程可得x′(t1)=λ >0,取充分小的∊,在(t1−∊,t1)上有x(t)≤0,与假设矛盾,故对所有的t>0,都有x(t)>0.

当t ∈[0,τ]时,由系统(1.3)的第二个方程可得

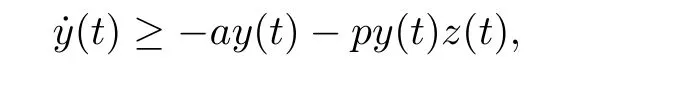
直接求得

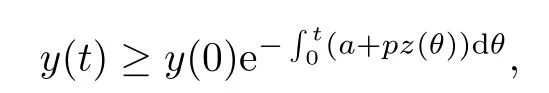
由y(0)>0可知,y(t)>0,t ∈[0,τ].由数学归纳法可以证明,对所有的t>0,都有y(t)>0.通过系统(1.3)的第三个方程直接计算可得:

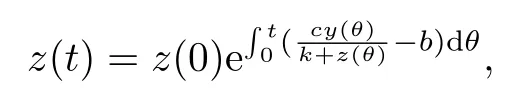
故系统(1.3)的解都是非负的.特别地,如果x(0)>0,y(0)>0,z(0)>0,则(1.3)的解都是正的.

下面证明解的有界性.令:

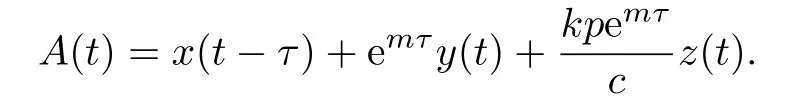
沿着系统(1.3)计算A(t)的全导数可得:

是系统(1.3)的正不变集.

§2 基本再生数和可行平衡点

系统(1.3)总存在一个病毒未感染平衡点E0(λ/d,0,0).利用下一代矩阵的方法[19]计算可得系统(1.3)的基本再生数为

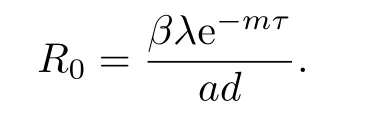
如果R0>1,则系统(1.3)存在一个免疫未激活感染平衡点E1(x1,y1,0),其中

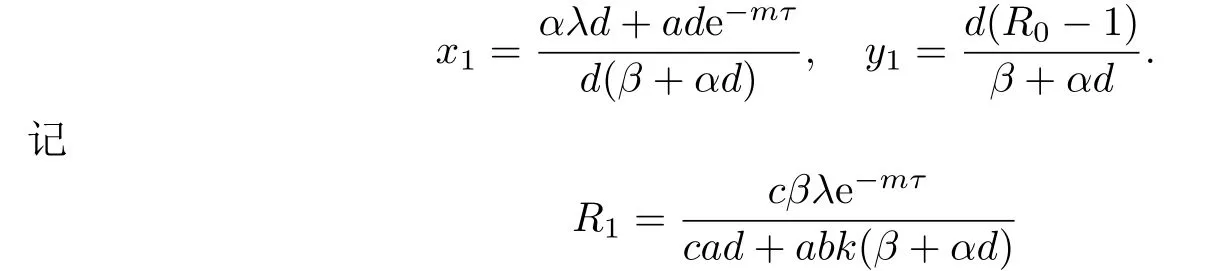
称R1是免疫反应再生数.易知,当R1>1时,系统(1.3)存在一个免疫激活感染平衡点E2(x2,y2,z2),其中

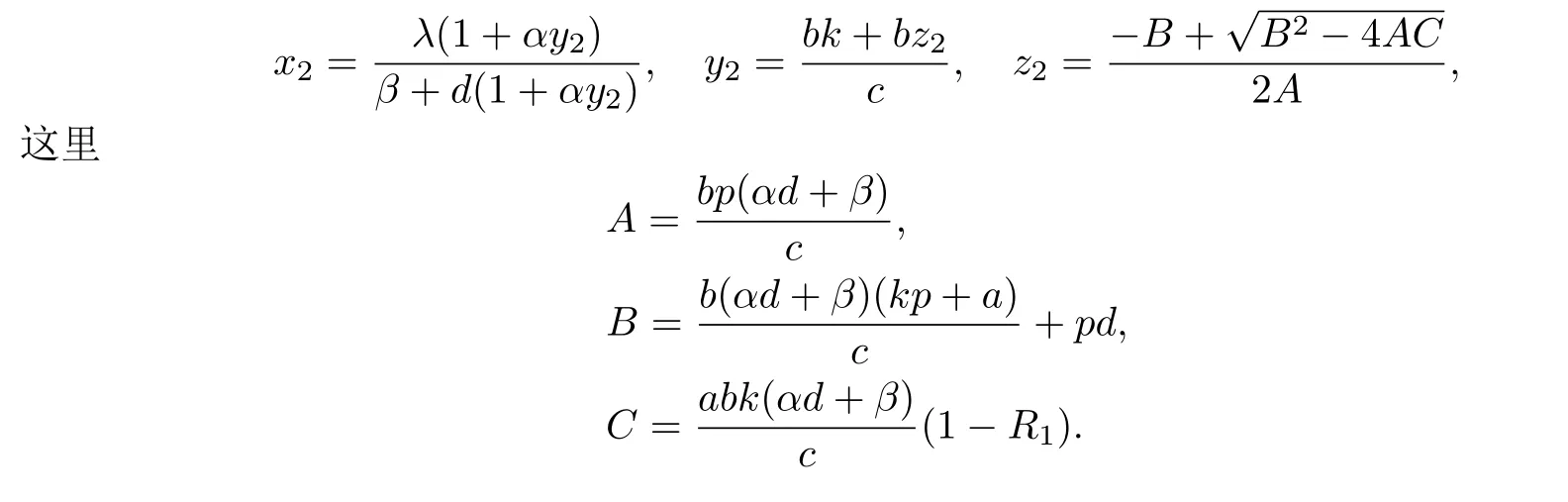
§3 可行平衡点的局部稳定性

本节通过分析相应特征方程根的分布,讨论系统(1.3)的可行平衡点的局部稳定性.

定理3.1对于系统(1.3),若R0<1,则病毒未感染平衡点E0(λ/d,0,0)是局部渐近稳定的,若R0>1,则E0是不稳定的.

证系统(1.3)在E0处的特征方程为

显然方程(3.1)总有负实根s=−d,s=−b,其他根由方程

确定.

以下证明,当R0<1时,方程(3.2)的根均有负实部.若否,则方程(3.2)存在根s1=a1+ib1,a1≥0.此时有

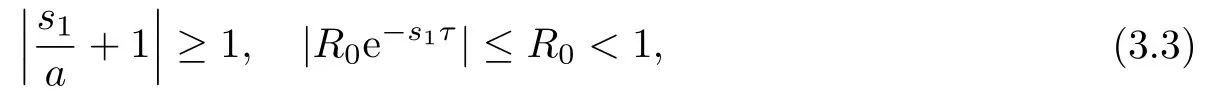
这与(3.2)矛盾.因此若R0<1,则方程(3.1)的所有根均有负实部,从而E0是局部渐近稳定的.

当R0>1时,G(s)是关于s的连续函数并且满足G(0)=1−R0<0,,因此方程(3.1)至少有一个正实根,故E0是不稳定的.

定理3.2对于系统(1.3),若R0>1>R1,则免疫未激活感染平衡点E1(x1,y1,0)是局部渐近稳定的.

证系统(1.3)在E1处的特征方程是

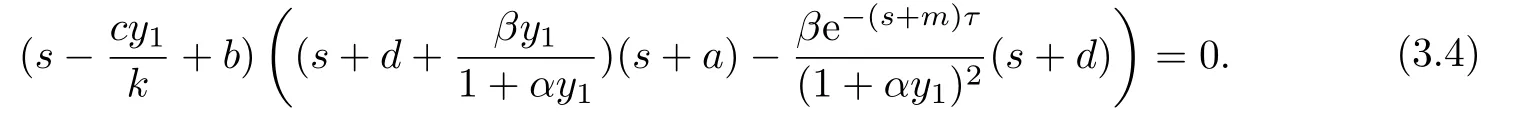
显然方程(3.4)总有负实根,其他根由以下方程

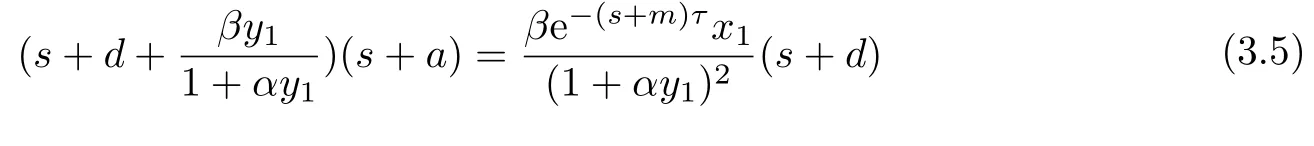
确定.

以下证明,当R0 >1 >R1时,方程(3.5)的根均有负实部.若否,则方程(3.5)存在根s2=a2+ib2，a2 ≥0.此时,有:

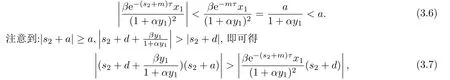
这与(3.5)矛盾.因此,若R0>1>R1,则方程(3.5)的所有根均有负实部,从而E1是局部渐近稳定的.

定理3.3对于系统(1.3),若R1>1,则免疫激活感染平衡点E2(x2,y2,z2)是局部渐近稳定的.

证系统(1.3)在E2处的特征方程是

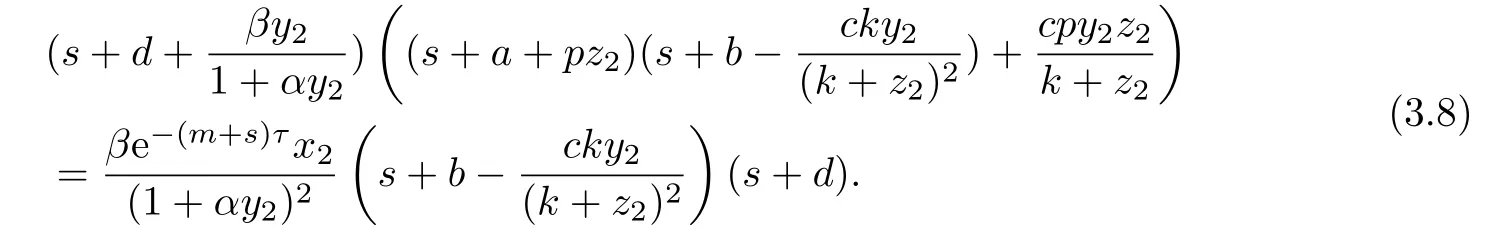
以下证明,当R1>1时,方程(3.8)的根均有负实部.若否,则方程(3.8)存在根s3=a3+ib3,其中a3≥0.此时有

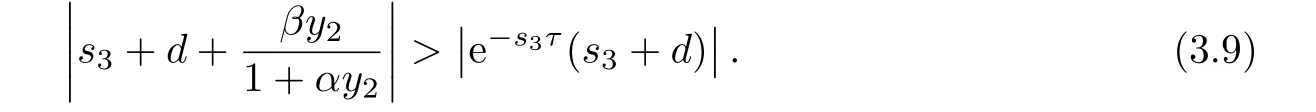
直接计算可得

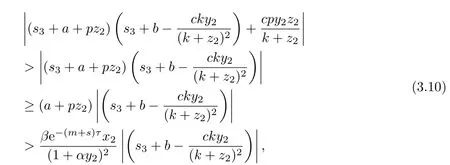
这与(3.8)矛盾.因此若R1>1,则方程(3.8)的所有根均有负实部,从而E2是局部渐近稳定的.

§4 可行平衡点的全局渐近稳定性

本节通过构造适当的Lyapunov泛函并结合Lasalle不变性原理来讨论系统(1.3)可行平衡点的全局渐近稳定性.

定理4.1若R0<1,则系统(1.3)的病毒未感染平衡点E0(λ/d,0,0) 是全局渐近稳定的.

证设(x(t),y(t),z(t))是系统(1.3)在初始条件(1.4)下的任意正解,定义

其中g(x)=x −1−lnx.显然g(x)>0,x/=1,g(1)=0.

沿着系统(1.3)计算V1(t)的全导数可得

定理4.2若R0>1>R1,则系统(1.3)的免疫未激活感染平衡点E1(x1,y1,0)是全局渐近稳定的.

定理4.3若R1>1,则系统(1.3)的免疫激活感染平衡点E2(x2,y2,z2)是全局渐近稳定的.

沿着系统(1.3)计算V3(t)的导数可得

§5 敏感性分析

本节对病毒感染再生数和免疫反应再生数进行敏感性分析.在系统(1.3)中,相应的参数取值如表1所示.

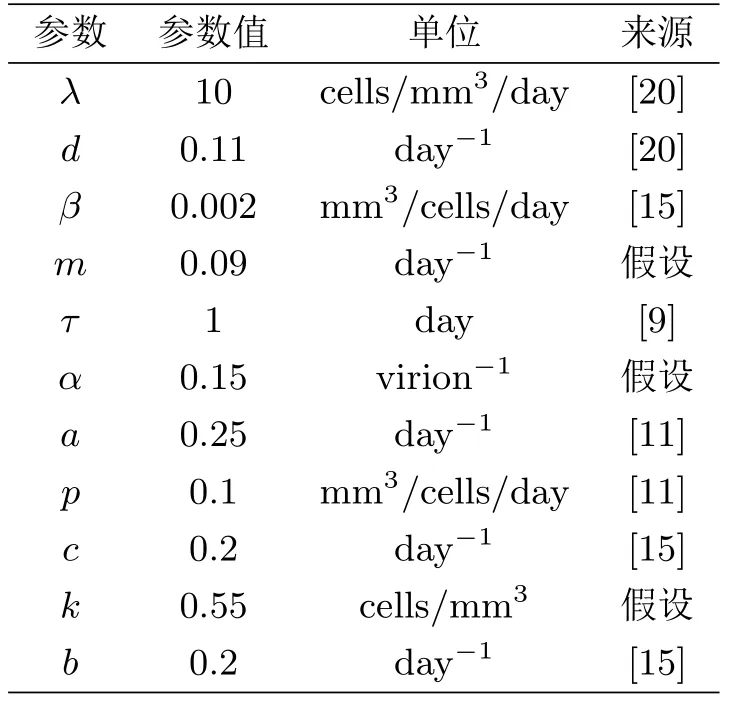
表1 系统(1.3)的参数取值

敏感性分析用于量化再生数的变量范围,并确定引起再生数变化的关键因素.近年来,拉丁超立方抽样被证明是一种更有效的统计抽样技术,已被引入疾病建模领域[21].文献[22]指出偏执相关系数提供了参数和再生数之间线性关联强度的度量.偏执相关系数的正负分别表示参数与再生数的正相关或负相关,其大小衡量了这种相关性的强度.因此,为了对病毒感染再生数和免疫反应再生数进行敏感性分析,先利用拉丁超立方抽样对参数空间进行抽样,再计算偏执相关系数.由图1(a)可知,对于病毒感染再生数R0,λ,β是正相关变量,m,τ,d,a是负相关变量,按相关强度顺序依次是:λ,β,d,a,m,τ;由图1(b)可知,对于免疫反应再生数R1,λ,β,c是正相关变量,m,τ,α,d,a,k,b是负相关变量,按相关强度顺序依次是λ,β,d,a,k,τ,m,c,α,b.

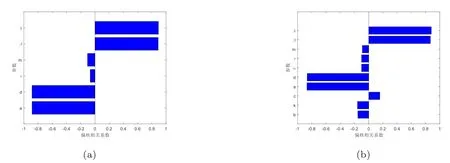
图1 病毒感染再生数R0和免疫反应再生数R1的敏感性分析

§6 结论

本文研究了一类具有胞内时滞,饱和感染率及饱和CTL免疫反应的HTLV-I感染动力学模型.通过严格的数学分析,建立了系统(1.3)的阙值动力学.通过构造适当的Lypunov泛函,证明了病毒未感染平衡点E0,免疫未激活感染平衡点E1和免疫激活感染平衡点E2的全局稳定性由病毒感染再生数R0和免疫反应再生数R1的值完全决定:当R0<1时,未感染平衡点E0全局渐近稳定,病毒被清除;当R0>1>R1时,免疫未激活感染平衡点E1全局渐近稳定,感染持续但免疫未被激活;当R1>1时,免疫激活感染平衡点E2全局渐近稳定,HTLV-I进入慢性感染期.