一类脉冲微分方程的光滑多尺度解
陈华雄,王岩岩*,刘 伟
(周口师范学院 数学与统计学院,河南周口 466000)
§1 引言
许多实际问题往往存在碰撞,开关,阈值,脉冲控制和数字控制等大量的非光滑因素,它们主要是由约束条件,本构关系和控制方式决定的.非光滑因素在现代科技各领域的实际问题中普遍存在,其数学模型往往可归结为非光滑动力系统.非光滑动力系统近年来一直受到学者们的广泛关注.从最新的科技成果表明,该类系统在控制系统,信息科学,生物,材料,管理,航天技术,经济等各领域中均得到重要的应用[1-3].
脉冲微分方程属于非光滑动力系统范畴,是向量场含有瞬时脉冲作用的动力系统,是前沿的数学分支,其充分考虑到瞬时突变对状态的影响.因此,该类方程具有显著的特征:脉冲微分方程的解是片段连续的,不连续点发生在瞬时突变时刻,即脉冲时刻.正由于这一特征,使得脉冲微分方程的研究变得丰富,也带来了一定的困难.迄今为止,已有诸多的方法用于研究脉冲微分方程解的存在性[4],稳定性[5],分支[6]等.
鉴于脉冲微分方程解的不连续性,文[7]利用奇异摄动方法,通过引入适当的奇异摄动项,将脉冲方程的右问题扩充成具有无穷大初值的奇异摄动问题,从而得到连续的渐近解来有效地刻画原脉冲问题的不连续解.而本文将提供一种以光滑的多尺度解的观点来刻画脉冲微分方程.通过引入适当的奇异摄动项,不同于文[7],本文定义了一类具有临界情况的奇异摄动边值问题,同样地其对应的退化方程为原脉冲微分方程.利用边界层函数法[8]和缝接法[9],构造了该奇异摄动边值问题的光滑形式多尺度解,并给出了多尺度解的存在性及余项估计.
不失一般性,本文考虑在区间[0,T]具有一个脉冲点的脉冲微分方程

为了阐明本文的思想,现引入如下的二阶奇摄动边值问题

这里0<∊≪1为小参数,Sgn为符号函数.为了得到问题(3)的解,将(3)写成如下两个子问题

其中,Q(∊)=Q0+∊Q1+∊2Q2+……,K(∊)=K0+∊K1+∊2K2+……,而Qi,Ki为待定参数.
根据奇异摄动理论[8]可知,问题(4)和(5)在t=t0处存在边界层,其对应的退化方程(令∊=0)分别为
当0≤t 当t0 比较(2)以及(6)和(7)的解,则问题(3)的退化方程的解可视为区间[0,T]上的脉冲微分方程(1)的解.因此,根据奇异摄动理论[8],当∊→0时,问题(3)的解可有效地刻画脉冲微分方程(1)的解. 从(4)和(5)可以看出,问题(3)的解在t=t0处是连续的,为了使其光滑,还需满足如下条件 这也是确定Qi,Ki的方程. 将问题(4)化为如下等价的方程 则问题(9)存在右边界层,构造其如下形式的多尺度解 将(11) 和(12) 代入(9)中,通过分离变量t和τ后,两端对∊进行幂级数展开并比较∊的同次幂系数,则确定正则级数主项所满足的方程和 以及边界层项的主项R0zi(τ),R0yi(τ)所满足的方程 将问题(5)化为如下等价的方程 则问题(23)存在左边界层,构造其如下形式的多尺度解 以及边界层项的主项L0zi(τ),L0yi(τ)所满足的方程 由光滑性条件(8),可得 (1)Q0,K0的确定 将(15),(16) 和(29),(30) 代入(33),可得 解(36)和(37),得 (2)Qk,Kk的确定 从(21),(22),(31),(32) 以及(34),(35),可得 利用“缝接法”证明问题(3)多尺度解的存在性,同时给出解的渐近表达式.所求问题的多尺度解可以看成两个具有纯边界层P(−)和P(+)的解在t=t0处光滑缝接而成. 问题P(−)(0≤t ≤t0) 问题P(+)(t0≤t ≤T) 可见当∊充分小,并且取δ为异号值时,也异号,所以由介值定理,存在Q∗∈[Qn−δ,Qn+δ],使得L(Q∗,∊)=0.同理可证K∗的存在性. 定理3.1存在充分小的∊0,当0<∊<∊0时,问题(3)的光滑多尺度解yi(t,∊)存在,且具有如下的渐近表达式当0≤t ≤t0时 当t0≤t ≤T时 注若在定理3.1 中取i=0,则得到的光滑多尺度解 当0≤t ≤t0时 当t0≤t ≤T时 取∊充分小时,则首阶多尺度解是脉冲问题(1)解的一个很好的刻画. 考虑如下具有单个脉冲点的经典的Volterra捕食与被捕食模型 其中,y1(t)表示害虫的种群数量或种群密度,y2(t) 为天敌的种群数量或种群密度,a,b,c,d均为正常数,−p1和p2分别表示在t=t0时刻所喷洒的农药使得害虫的减少量和投放的天敌的数量. 根据本文的思想,定义如下的二阶非光滑奇异摄动边值问题 其中,ϕ(+)(t),ψ(+)(t)为问题(38)的解. 为验证本文的结果,这里取 通过数值模拟,从图1和图2,可以看出,用本文的方法所构造的光滑多尺度解是原脉冲问题(38)的一个很好的刻画.而∊的不同值,则刻画了光滑解在脉冲点t=t0处的瞬变程度.∊越小,瞬变程度则越厉害. 图1 原脉冲问题(38)的间断解y1,y2关于t的图形 图2 奇异摄动问题(39)的首阶光滑多尺度解y1,y2关于t的图形,其中---, ∊=0.1;_____, ∊=0.0001 本文说明了奇异摄动是研究脉冲微分方程的一种有效的方法,它可提供一种以光滑的多尺度解的观点来刻画原脉冲微分方程,从而为进一步揭示脉冲现象提供了崭新的途径.在此方法中,重要在于定义对应的奇异摄动边值问题.该方法也可以推广到更复杂的脉冲微分方程,如依赖于状态的脉冲微分方程等.

§2 脉冲微分方程及光滑的多尺度解的构造

2.1 问题P(−)多尺度解的构造
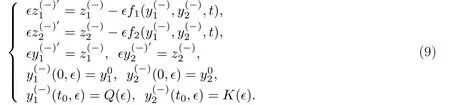




2.2 问题P(+)多尺度解的构造

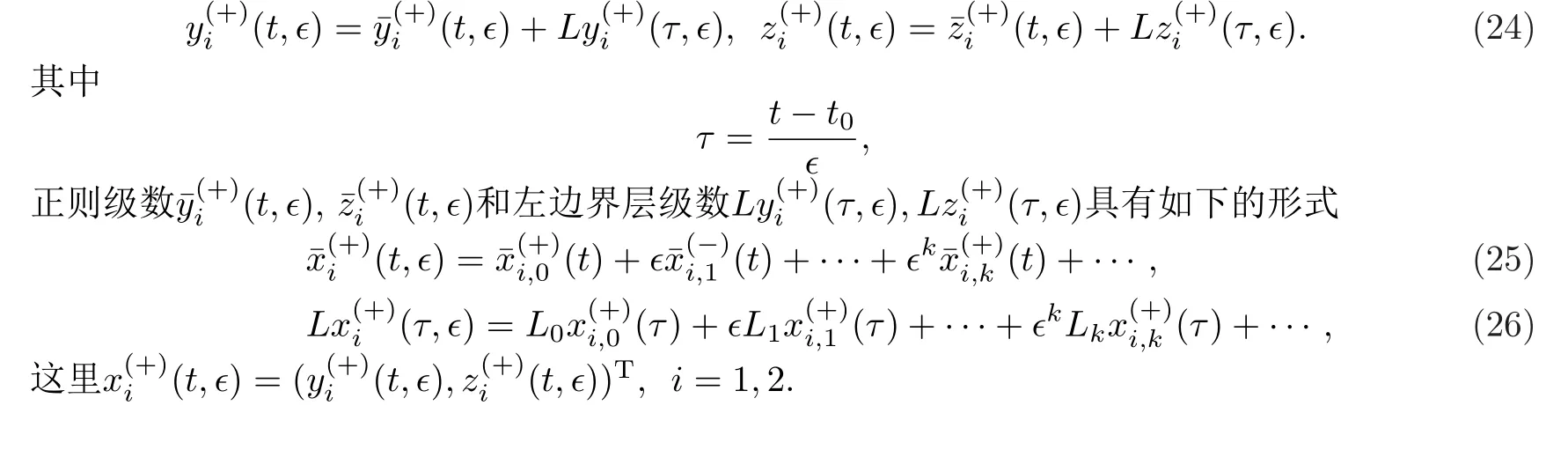



2.3 参数Qk,Kk的确定




§3 解的存在性与余项估计


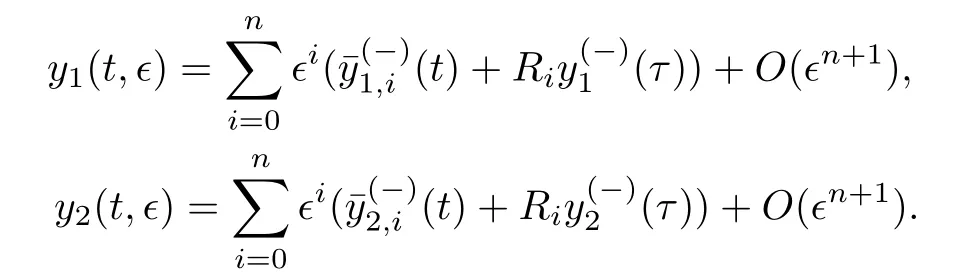


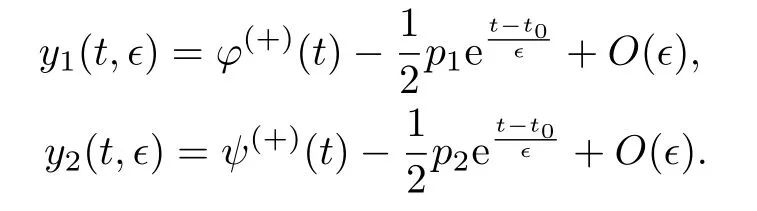
§4 例 子


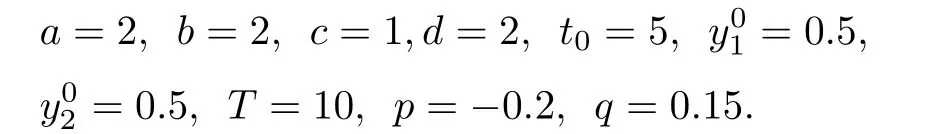


§5 结论

