一类变化区域中的粪口模型的传播动力学

刘梦丽,朱 敏,宋小飞

(安徽师范大学 数学与统计学院,安徽芜湖 241000)

§1 引言和模型建立

近年来,传染病的大规模间断性暴发严重影响了社会公众的健康.传染病的传播具有多种媒介,例如,有通过蚊子传播的蚊媒疾病,有通过空气传播的呼吸道疾病,有通过排泄物传播的粪口疾病等.常见的粪口传播是指传染源消化道内含有的病原体通过粪便排出体外,污染水源和食物,然后通过各种形式经过消化道间接进入人体造成感染,故粪口传播又称为消化道传播.粪口疾病种类众多,比较常见的粪口传播疾病有霍乱[1],细菌性痢疾[2],手足口病,还包括绦虫病,蛲虫病,蛔虫病等一些寄生虫疾病[3].虽然能够通过有效切断传播途径从而降低粪口疾病的感染率,但在一些偏远及经济相对落后的地区,公共卫生知识的缺乏导致粪口疾病不断流行,而在一些公共场所,各种环境卫生问题的存在也导致无法完全切断粪口疾病的传播,因此对于粪口传染病的研究仍然至关重要.

针对粪口传播模型,许多学者从不同角度探讨了粪口传染病的传播机理.文献[4]将自由边界引入到一类反应扩散粪口模型,探究了感染区域的扩张能力对病毒传播的影响;文献[5]重点研究了合作和部分退化的反应扩散系统,通过上下解方法揭示了单稳态波阵面的存在性,得到了单稳定波阵面的最小波速与传播速度一致的结论;在文献[6]中,作者关注了具有非局部项和双自由边界的部分退化系统,分析出非局部项和双自由边界弱化了疾病的传播风险;在霍乱细菌扩散而感染者不扩散的情形下,Zhao和Wang[7]利用不动点定理以及上下解方法探讨了单稳态非线性条件下系统单调行波解的存在性.

事实上,由于气候变化和人类活动领域的不断扩张,种群栖息地和病毒的生存范围都在不断发生变化.因此,对于生物种群的持续和灭绝来说,生存区域的变化是不可忽略的一个因素.许多学者都关注了区域变化对自然科学、生命科学以及医学等领域的影响[8-10].本文将在以下Capasso和Maddalena提出的霍乱微分方程模型[1]的基础上,重点探讨区域变化对粪口模型传播动力学的影响,

并同时给出了判断稳定性的阈值参数

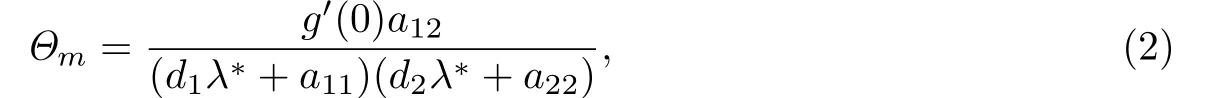
这里的λ∗是−Δ算子在齐次边界条件下的主特征值.为了后文书写方便,首先给出如下记号

Dt=Ω(t)×(0,+∞),D0=Ω(0)×(0,+∞),Bt=∂Ω(t)×(0,+∞),B0=∂Ω(0)×(0,+∞),这里Ω(t)⊂Rn是一个随时间t变化的区域,∂Ω(t)为其边界,Ω(0)为初始域.根据文献[11-13],对于在Ω(t)内的任意点x(t),细菌种群密度为u1(x(t),t),感染性人类密度为u2(x(t),t),由质量守恒原理和Reynolds输运定理[14],在(x,t)∈Dt时有如下演化域上的粪口模型,

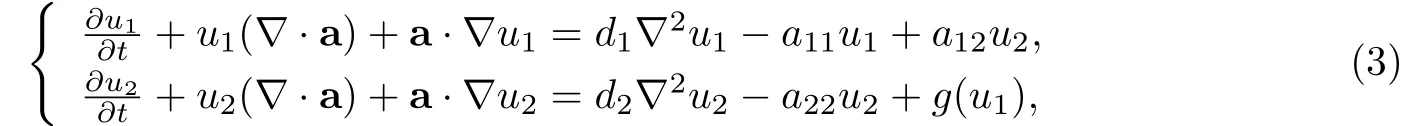
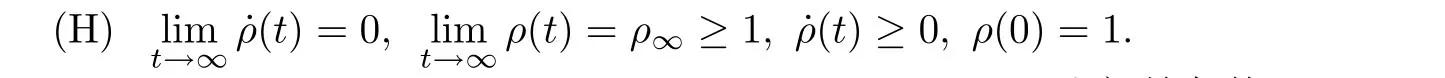
考虑问题(3)具有齐次的Dirichlet边界条件u1(x(t),t)=u2(x(t),t)=0和初始条件(u1,u2)=(u1,0(x),u2,0(x)),其中初始条件为正的有界连续函数,令

利用[13,15]类似的方法,则问题(3)与其初始条件和边界条件可以转换为如下形式

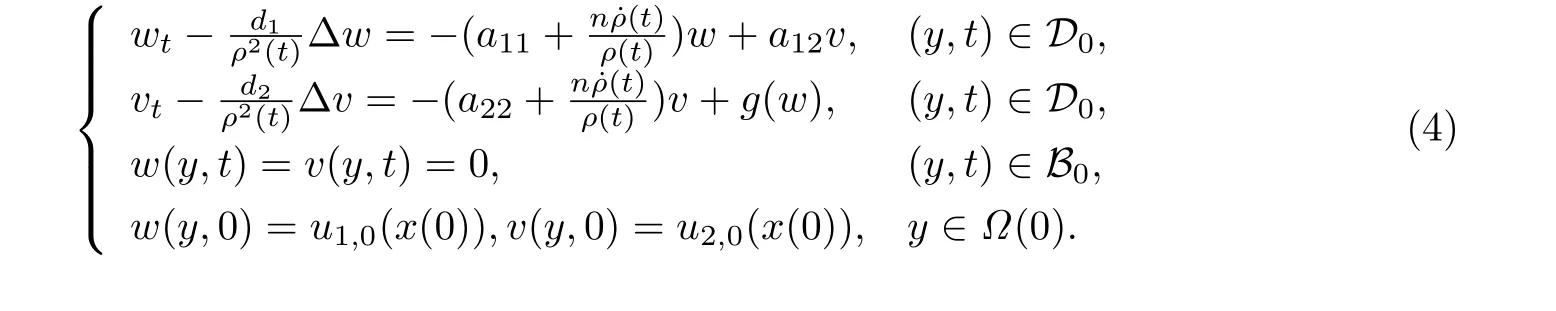
§2 基本再生数

基本再生数表示在完全易感人群中由一个典型的受感染个体在平均患病期间内所产生的平均继发性病例数,是非常重要的一个传染病阈值.一般来说,对于由常微分系统所刻画的传染病模型,基本再生数可以通过下一代矩阵法[16]算出,而模型(3)和(4)均为反应扩散系统,将利用特征值问题和下一代感染算子的谱半径求解[17].

首先考虑模型(4)的极限系统如下

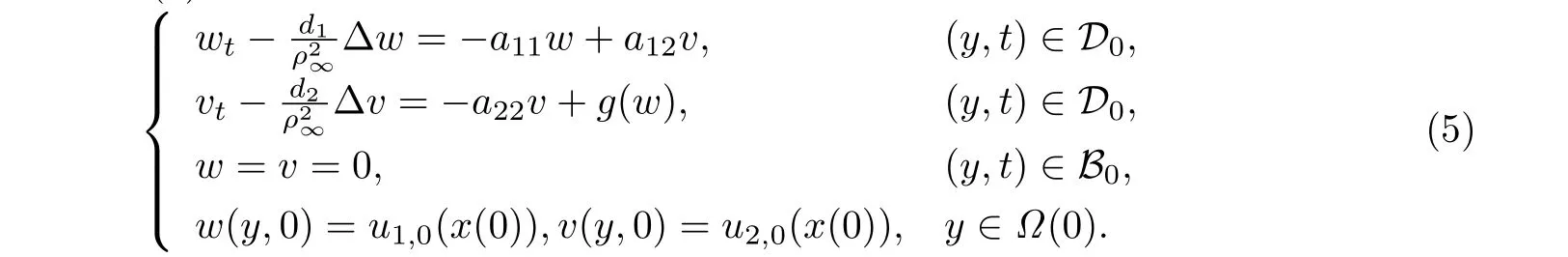
将模型(5)在无病平衡点(w,v)=(0,0)处线性化后可以得到以下方程:

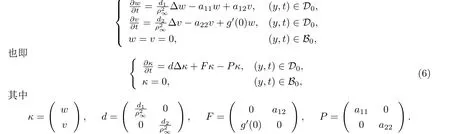
根据文献[17]中对基本再生数的定义可知,问题(6)中感染仓室内个体的自身演变是由以下的线性反应-扩散方程组所决定的,

同时还能够得到关于的其它相关结论.

定理2.1以下论断成立.

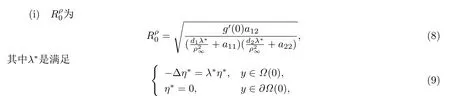
的主特征值,这里η∗是λ∗对应的特征函数.

(ii) 在问题(7)中当y ∈Ω(0)时,−Δφ(y)和−Δψ(y)恒大于0.

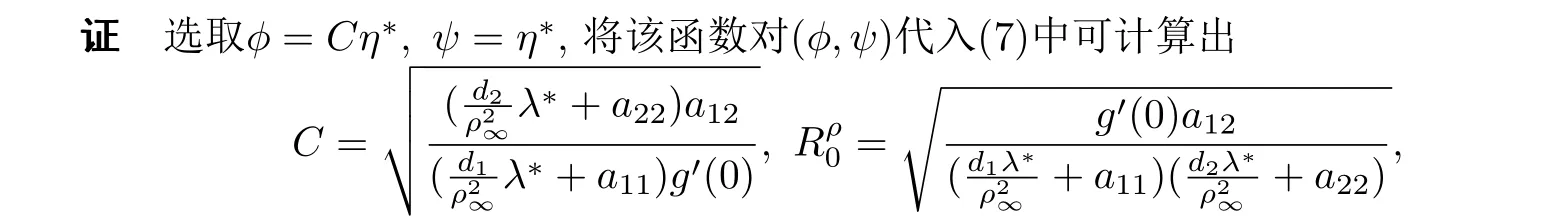
并由(7)中主特征对的唯一性可知()就是(7)的解.因此,结论(i)成立.并注意到φ,ψ与η∗的关系,结合(9)可判断(ii)也成立.

在条件(G1),(G2)及(H)下,将利用上下解方法来探讨区域变化对问题(4)动力学行为的影响.为了便于比较,将依次给出固定域上的情形和变化域上的情形.

§3 固定域对粪口疾病的影响(ρ(t)≡ρ∞≡1)

在考虑区域变化对粪口疾病动力学的影响之前,首先给出上下解定义和比较原理.

以及对应的特征值问题

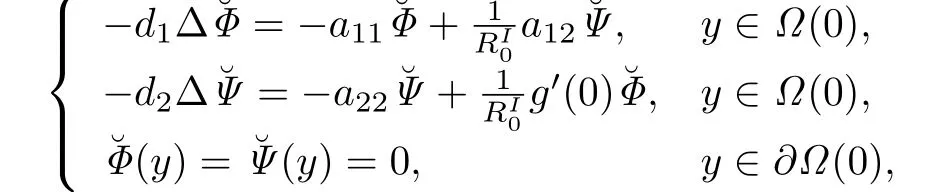
然后再根据定理2.1中的相关计算可知问题(10)的基本再生数为

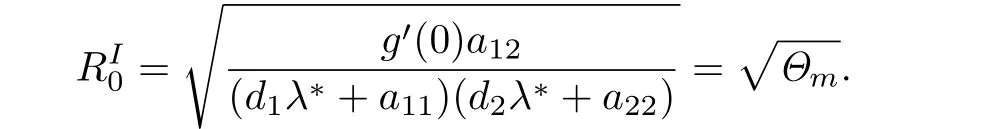
这里的Θm是文献[1]中阈值,由(2)式给出.下面先给出固定域上问题(10)的动力学结论,相关证明在后文中阐述.

定理3.1当1时,系统(10)的平凡解(0,0)全局渐近稳定.

§4 变化域对粪口疾病的影响(ρ(t)/≡ρ∞)

如果ρ(t)/≡ρ∞,此时Ω(t)是一个变化区域,下面首先探讨1时问题(4)的动力学.

引理4.2如果0>1,则存在T0>0,使得当t ≥T0时,(M1,M2)和(∊0φ,∊0ψ)是问题(4)的上下解,这里(M1,M2)由(17)定义,∊0充分小且(φ,ψ)是特征值问题(7)的主特征函数对.

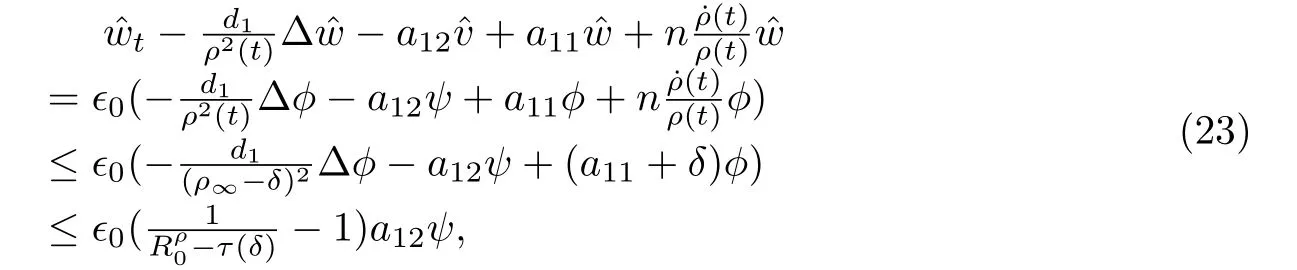
类似于(16),又有

现在考虑辅助问题(21)分别伴随不同的初始条件

这里的T0由引理4.2定义,有如下引理.

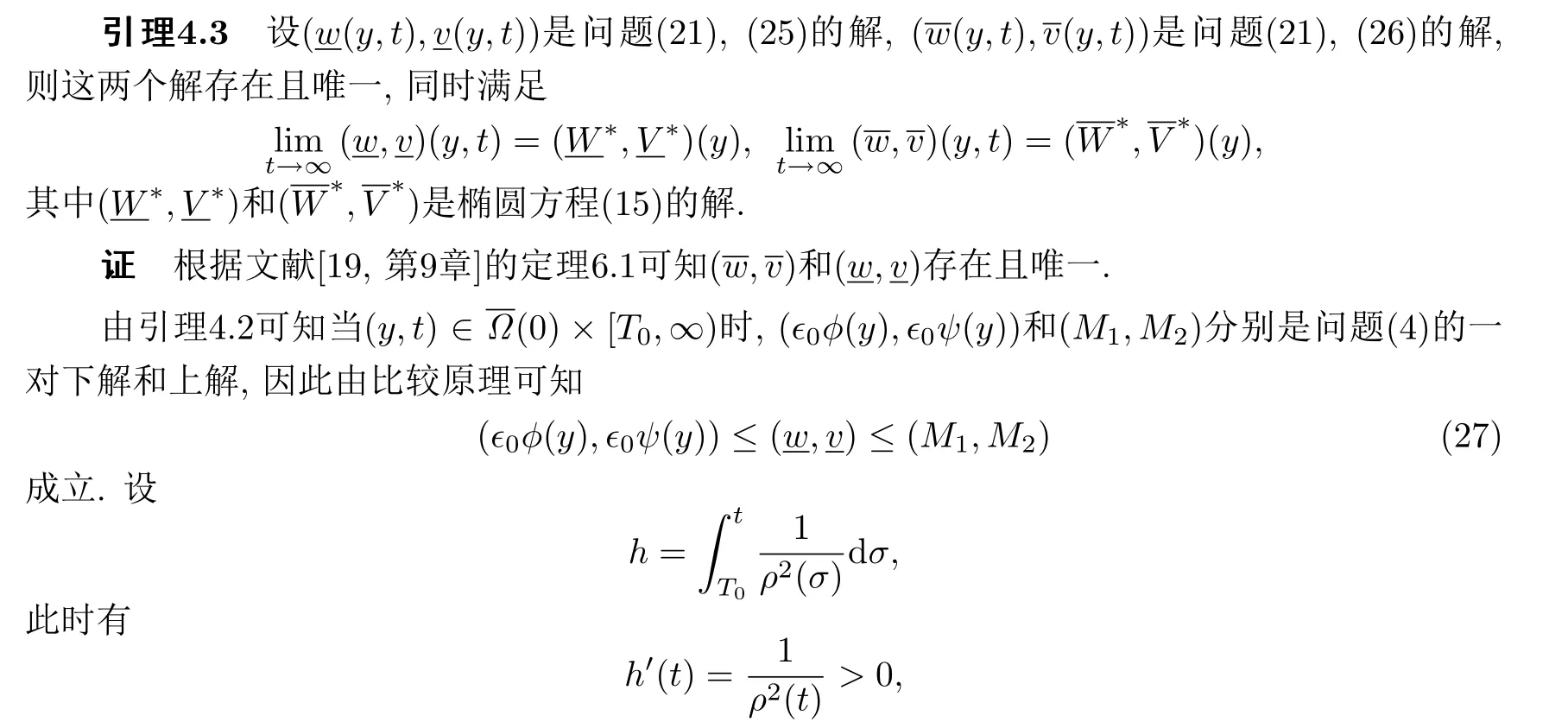
则存在逆变换t=f(h)使得

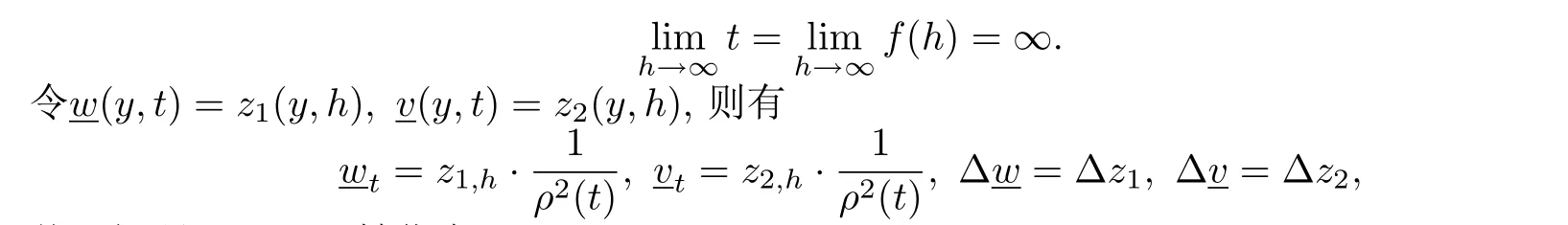
从而问题(21),(25)转化为

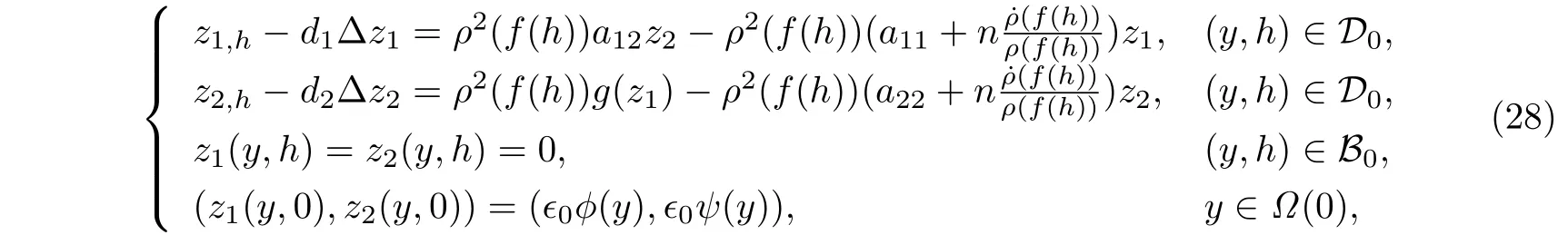
显然,问题(28)仍然是一个合作系统,但其扩散系数已变为常数.回顾关系式(27),有

注对于固定区域中定理3.1和定理3.2的证明,可以分别通过定理4.1和定理4.2的证明在ρ(t)≡1的情况下推导得出.

§5 数值模拟和流行病学分析

现在选择不同的演化率ρ(t)来模拟问题(4)解的长期行为.

模拟5.1选取较大的演化率

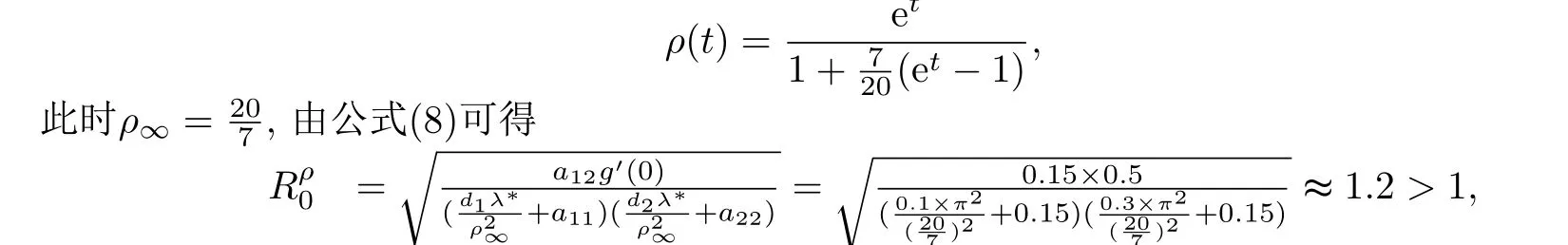
根据定理4.2可知当1时,问题(4)的任意解介于椭圆系统(15)的最大解和最小解之间,这意味着粪口病毒将会传播.通过图1(a)可以观察出变量w(y,t)趋于一个正稳定态,通过图1(b)和(c)能够看出区域Ω(t)的增长趋势以及粪口病毒的变化趋势.

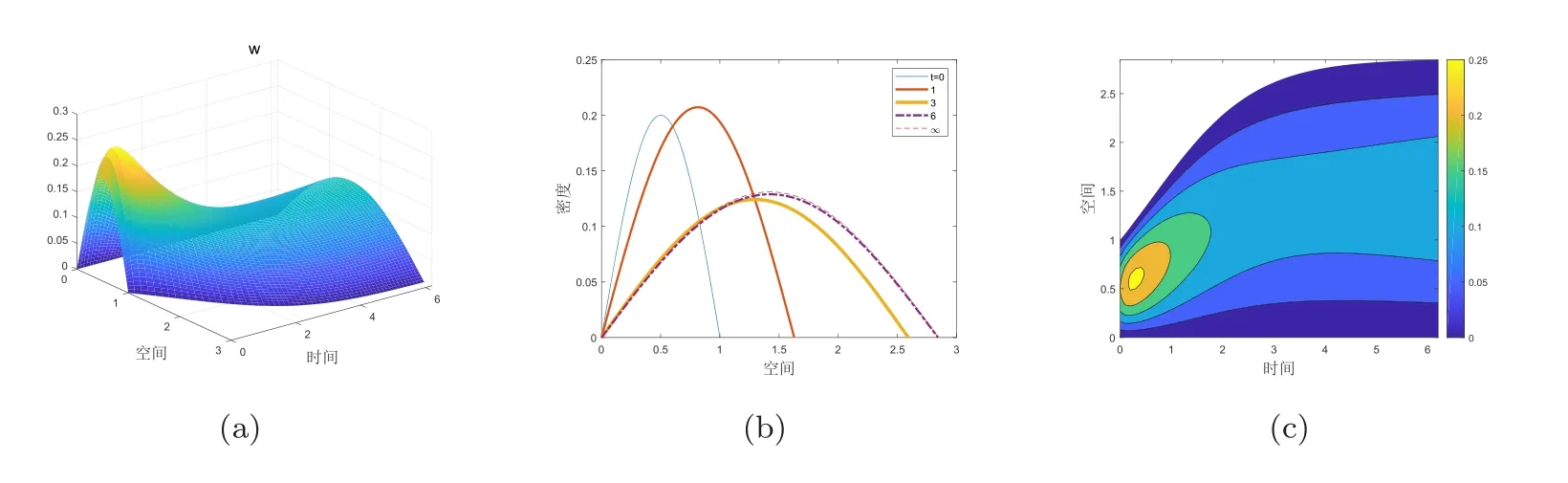
图1

定理4.1表明问题(4)在1时,(0,0)全局渐近稳定,而图2(a)中也显示出(4)的解最终趋于无病平衡点,这意味着粪口病毒将逐渐消失.由图2(b)(c)能够看出区域Ω(t)在不断增大.

图2

基于Capasso和Maddalena提出的模型(1),深入研究了区域的变化对粪口传染病传播的影响.在探究模型(4)解的长期行为的过程中,首先给出了演化率ρ(t)的相关假设,然后通过下一代感染算子的谱半径以及相应的特征值问题计算出基本再生数(8),将其作为判断问题(4)解的稳定性的阈值参数.由于抛物系统(4)具有和时间相关的扩散系数,在利用上下解方法判断解的渐近行为的过程中会出现前文中提到的两个困难,而通过引理4.2和4.3可以克服了这两个困难,并且建立了抛物系统(4)和椭圆系统(15)的解之间的关系.最后通过定理4.1和4.2,可以发现当1时,问题(4)具有平凡解(0,0),并且全局渐近稳定,这意味着粪口病毒和感染人群将逐渐消失,当1时,〈(∊0φ,∊0ψ),(M1,M2)〉是问题(4)的吸引域,这表明粪口病毒和感染人群将会逐渐扩散.

在文献[13]中,作者考虑了区域增长对单一物种的昆虫扩散模型的影响,得出结论:区域的增长对正稳态解的渐近稳定性有积极影响,而对平凡解的渐近稳定性有消极影响,这意味着区域的演化会促进昆虫的扩散.相对于单一物种模型,给出了两个不同物种的模型(4),根据第三部分的分析,也即演化域和固定域的对比可知,当1时,粪口病毒和感染人群在固定域和演化域上都将消失;当1时,粪口病毒在固定域上将会消失,在演化域上将会传播;当1时,粪口病毒在固定域和演化域上都会传播.结果说明较大的演化率会进一步增加粪口病毒传播的风险.综合来看,栖息地的扩张会促使物种的蔓延包括病毒的扩散.在现实生活中,随着气候变化和人类生存环境的改变,适合病毒生存的空间也在不断增大,这使得病毒的传播风险增加.通过以上分析意识到,减缓全球气候变暖的速度,适当控制人类的活动范围能够有效地控制粪口病毒的传播.