结论众多 通法何在——2020年导数压轴题引发的思考

谢贤祖

(华南师大附中汕尾学校 516600)

一、勤于积累，利于解题

在旧教材人教A版选修2-2第32页的习题1.3 B组第1题涉及几个常见的不等式.

例1 求证： sinx1+x(x≠0)，lnx0).

众所周知，这几个不等式非常重要，在证明函数不等式或者放缩过程中有着举重若轻的作用，甚至有很多老师和网络大神还总结了更多的不等式，使得它们成为解题利器，并要求学生背诵，以备不时之需，下面先梳理最为常见的和笔者自认为重要的结论并汇总如下.

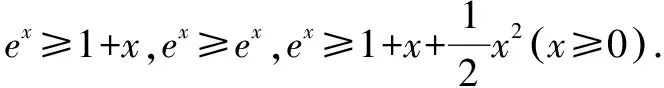
证明过程较为简单，此处从略.下面笔者先结合2020年高考导数题，分析一下解题思路，展示一下这几个结论的妙用，再谈谈个人的感悟与思考.

例4(2020年山东21题·节选)f(x)=aex-1-lnx+lna.若f(x)≥1，求a的范围.

分析先用“必要性探路”.由题意，得f(1)=a+lna≥1.而g(a)=a+lna是增函数，且g(1)=1，由g(a)=a+lna≥g(1)⟹a≥1.下面先证明a=1时，f(x)≥1恒成立.当a=1时，f(x)=ex-1-lnx.由常见不等式ex≥1+x和x-1≥lnx可得ex-1≥x≥lnx+1.

所以f(x)=ex-1-lnx≥1.所以当a≥1时，f(x)=aex-1-lnx+lna≥ex-1-lnx≥1.

总结其实例4所考查的关键不等式：ex-1-lnx≥1，在2013年全国Ⅱ卷21题中考过.题目展示如下：已知函数f(x)=ex-ln(x+m),当m≤2时，证明f(x)>0.所以是旧题重考，略有创新.这两道题都是经典好题，使用常见不等式链ex-1≥x≥lnx+1便可轻松解决，值得作为高三复习的重点素材.

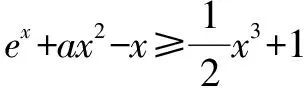
令h′(x)=0，可得x=2.当x∈(0,2)时，h′(x)>0，所以h(x)在x∈(0,2)单调递增；当x∈(2，+∞)时，h′(x)<0，所以h(x)在x∈(2，+∞)单调递减.

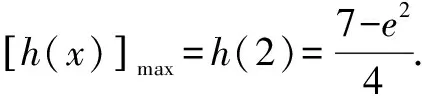
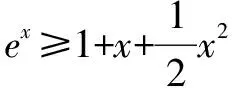
例6 (2020年浙江卷22题)已知函数f(x)=ex-x-a(1

(1)证明：f(x)在(0,+∞)上有唯一零点;

(2)设x0是f(x)在(0,+∞)上的唯一零点，证明：

②x0f(ex0)≥(e-1)(a-1)a.

总结上述解法用到常见不等式ex≥1+x,ex≥ex，但是如何想到使用这两个不等式而不使用其它以及如何优雅的一路畅通证明不等式，是需要经过不断尝试、遇到挫折、再调整才能想到的.

二、追本溯源，总结反思

1.恒成立问题首选分离参数，这是比较好想的，但并不是什么时候都能做出，所以还需引导学生如果遇到困难，就要调整策略，这应该也要成为解题的“通用思维”.而通过“代点”“必要性探路”“先猜后证”来解决恒成立问题也是非常体现数学思想的，应该纳入“通性通法”的范畴.

2.构造函数、求导、因式分解、判断导函数符号、结合画图、讨论单调性再用之解题应该成为永恒不变的主旋律.如果一次求导不能解决问题则可以尝试多次求导，这也是正常操作，如果多次求导后还解决不了问题则需要另寻出路.

3.零点存在性定理是证明函数零点存在的通用方法，也是“卡根”“求根的范围”的重要手段.

4.对要证明的不等式进行变形、转化直到找到证明思路是正常手段，如果在转化过程中出现自己总结过的常见不等式，则单独“抽出”并证明，所以平时多积累常见不等式或者自己不小心发现的“小结论”无可厚非，但对于一些不常见、不优雅、无规律的不等式只需见过就好，不必强求记忆.