高中物理解题中补偿法的应用

刘 鹤

(福建省永安市第一中学 366000)

补偿法是指通过补充习题中相关事物中的一部分，使其构成一个能够使用标准模型求解的解题方法.众所周知，高中物理很多的结论、定理有着一定的适用条件.为更好的将相关的结论、定理应用于解题中，应根据题干创设的情境运用补充法，快速找到解得突破口.

一、用于计算万有引力

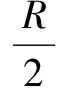
图1

A.4∶3 B.9∶7 C.4∶1 D.9∶6

应用点评球被挖去一个小的球体后，剩余部分是一个不规则的几何体，无法直接运用万有引力定律计算相关引力，而通过补偿法进行转化成一个完整的球体，将问题转化为求解两个球体间的万有引力之差问题也就迎刃而解.

二、用于计算电场力

如图2，一半径为R，绝缘均匀带电球壳所带的电荷量为+Q.在球心位置放置一电荷量为+q的点电荷.当在球壳上挖去一个半径为r(r≪R)的小圆孔时，则点电荷受到的电场力大小为( ).

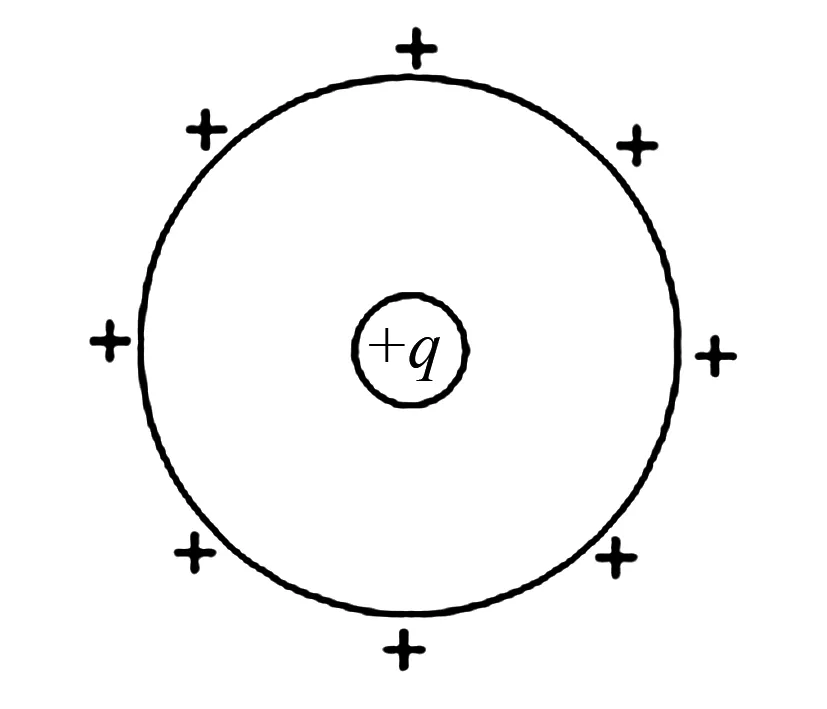
图2

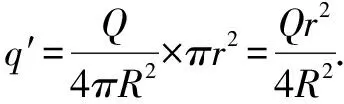
应用点评习题创设的情境较为抽象，无法直接求解.运用补偿法将其补充成一个完整的球壳，运用力的平衡知识便可很快的计算出点电荷所受的电场力.

三、用于比较场强大小

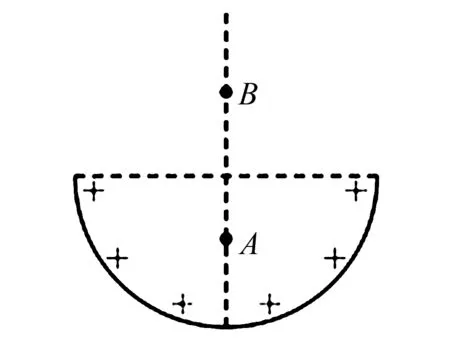
如图3所示，一半球壳表面带有均匀的正电.沿轴线将其分为厚度相同的两部分.将两部分置于相距非常远的距离，其仍均带电，则左右两部分在A1、A2产生的场强大小分别为E1，E2，则( ).

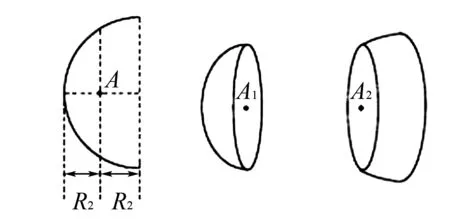
图3

A.E1=E2B.E1

C.E1>E2D.不确定

以左边部分为研究对象，采用补偿法将其补充成一个完整的球，因均匀带电球体内部的场强为零，因此，E1和补充部分产生的场强大小相等方向相反(设在A1产生的场强为大小为E3)，即，E1=E3.对于右边部分补充一个半球体，其在A2产生的场强大小E3>E2，因此，E1>E2，选择C项.

应用点评题目设计两个不规则的几何体，难以运用所学知识直接分析.运用补偿法，给两个部分补充相关的几何体，而后带电球体内部场强规律以及场强的合成法则问题也就顺利解决.

四、用于分析综合问题

如图4，一表面均匀带电的半球壳开口向上放置.A、B处在半球壳的对称轴上且关于半球心对称.则以下判断正确的是( ).

图4

A.A、B两点具有方向相同，大小相等的场强

B.半球心处的场强为零

C.A、B两点的电势可能相等

D.将一正电荷沿直线由A向B运动，电场力先做负功后做正功

通过审题易知采用补偿法可顺利突破该题.A项，将半球壳补充成一个完整的球壳，因在球壳内部的场强处处为零，则上半球壳在A点产生的场强向下，下半球在A点产生的场强向上，两者产生的场强大小等大反向.因为A、B两点关于半球心对称，若去掉上半球壳，则A、B两点场强大小相等，方向相同，正确.B项，有上半球壳时半球心处的场强为零，如没有上半球壳，则半球心处的场强不为零，错误.C项，从A到B电势逐渐降低，AB两点电势不可能相等，错误.D项，正电荷沿直线由A向B运动电场力一直做正功，错误.综上只有A项正确.

应用点评分析物理综合性问题时，既要注重根据题设情境对原有物体进行合理的补偿，以辅助分析，又要注重联系所学的物理规律，结论，认真分析相关物理参数的变化.

应用补偿法解答高中物理习题时，不同的习题类型采用的补偿思路有所区别.为提高学生应用的灵活性，教学中既要注重为学生灌输补偿的一般思路、方法，又要注重为学生做好应用补偿法解题的示范，同时鼓励学生做好听课以及日常训练的总结，总结一套适合自己的，运用补偿法解题的技巧.