规则波作用下垂直圆管负浮力射流的数值模拟
尹则高,王 盛,孙 灿
(1.中国海洋大学工程学院,山东 青岛 266100;2.浙江禹贡信息科技有限公司,浙江 杭州 311265)
射流是高浓度盐水和废水排放等工业领域常见的物理现象。根据射流流体与环境流体物理特性(密度、温度等)的差异,一般可将射流分为纯射流和浮力射流[1]。纯射流流体与环境流体物理特性一致,动力特性相对简单,对其研究较早且较完善。前人通过理论、实验和数值模拟的方法,得到了静水条件下纯射流的时均流速沿程分布、射流核长度、射流扩展率等相关经验公式,并得出了各断面的流速分布自相似且符合高斯分布的结论;与静水条件相比,波浪作用下纯射流与环境水体间相互作用明显增强,射流扩展宽度和紊动强度大幅增加,射流稀释能力显著提高[2-7]。然而,自然条件下射流流体与周围环境水体常存在密度差,形成复杂的浮力射流。静水条件下,诸多学者对浮力射流时均、紊动特性进行了实验研究和理论分析,得到了射流最大上升高度、稳态高度、撞击位置和各特征位置稀释度等经验公式[8-13]。波浪条件下,其时间尺度与射流时间尺度相近,波浪引起水质点往复运动会对浮力射流特性产生显著影响[14-15]。
本文建立规则波作用下垂直圆管负浮力射流的三维数学模型,着重分析波参数对射流中轴速度衰减和射流速度半宽的影响规律,探讨不同波-射流动量比下负浮力射流的振荡扩散机制。建立量纲一平均速度衰减系数、平均特征半宽经验公式,以期为工程实际提供参考。
1 数学模型
1.1 控制方程
三维波浪运动的控制方程为RANS形式。RNGK-ε模型考虑了紊流漩涡和浮力效应的影响,对负浮力射流的紊流特征具有较高的模拟精度。本研究中,射流流体与环境水体存在一定密度差,对常密度运动流体的连续性方程进行改写,得到考虑变密度影响的连续性方程:
(1)
动量方程:
(2)

紊动动能(K)方程:
(3)
紊动耗散率(ε)方程:
(4)
式中:αK和αε为紊流普朗特数;ueff为有效动力黏度系数;GK为由层流平均速度梯度而产生的紊流动能;Gb为浮力产生的紊流动能;YM为可压缩修正系项;C1ε、C2ε和C3ε为经验常数,分别取1.44、1.92和0.20。
利用VOF方法追踪水气界面的实时变化。
(5)
式中:F=F(x1,x2,x3,t)为水体体积分数。当F=1时,网格充满液体;当F=0时,网格充满空气;当0 在造波边界定义自由水面高度和水质点的速度来生成规则波,其波面高度变化(η)可以用下式表示: (6) 水质点水平速度: (7) 水质点垂直速度: (8) 式中:H为波高,m;T为波周期,s;k为波数,m-1;d为静水深,m;ω为波圆频率,s-1。 数值水槽末端采用孔隙率为0.7的多孔介质材料,减少波浪反射。利用质量动量法模拟负浮力射流源项;通过定义射流源的位置、形状和方向,求解器在源上自动生成这些粒子。使用隐式粒子-流体耦合法计算从时间步长N到N+1的粒子速度,近似的动量方程为: (9) (10) 求解方程(9)和(10),得 (11) 为验证所建立数学模型的可靠性,在中国海洋大学水动力学实验室中的波浪水槽进行了试验,水槽长25 m,宽1.0 m,高1.2 m,上述长宽高分别对应x,y,z方向;水槽前端为推板造波机,末端为多孔介质消波材料。射流装置布置在水槽中部,垂直喷口内径D=0.015 m,距离水槽底部h=0.10 m,射流出口中心坐标为(0,0,0)。水箱内盐水密度ρj=1 050 kg/m3(Dm=1.23×10-9m2/s),经进水管垂直射入密度ρa=1 000 kg/m3的清水中。利用进水管上安装的CN-8300型水泵提供并调节射流流量,利用进水管上安装的HR-LWGB-10型涡轮流量计监测流量。采用小威龙声学多普勒流速仪(ADV)测量波浪作用下射流纵剖面上的三维速度,采用波高仪观测波面过程。本文试验和数学模型静水深d=0.6 m。物理模型试验及数学模型示意如图1所示。 图1 物理模型试验及数学模型示意Fig.1 Sketch of experimental and mathematical model 本文利用FLOW-3D软件建立并求解上述数学模型。网格划分中,选用理查森外推法(Richardson extrapolation)计算离散误差,并用网格收敛指数(IGC)方法测试网格独立性。这里选取了3种不同尺寸的远场网格,S1=0.01 m,S2=0.02 m,S3=0.04 m;为了精确捕捉射流及波面附近区域的水动力特征,分别对上述3种远场网格划分下的波面和射流附近局部区域进行加密,加密网格尺寸分别为0.002 5 m,0.005 m和0.01 m。表1给出了波高H=0.10 m、波周期T=1.5 s、射流口直径D=0.015 m、射流口速度wj=1.57 m/s、t=17.8 s时距离造波端5 m处波面水质点速度、波面高度及计算误差。可以看出,网格1和网格2的离散误差较小,分别为0.7%和0.2%。图2(a)为距离造波端5 m 处的波面高度时程曲线。可以看出网格3与其他2种网格划分的计算结果出现了相对较大的误差,但是网格1和网格2之间的结果误差较小。图2(b)给出了t=20 s时沿水槽方向波面高度的空间分布,分别计算网格1、网格2和网格3划分条件下x=8 m和x=10.99 m处的波高,得到单位距离内相对波高衰减值分别为0.2%、0.31%和0.5%,相对较小,说明3种尺寸的网格划分不会对计算波面高度产生大的影响。综合考虑计算精度和时间的平衡,选择网格2参与后续数值计算。 表1 3种网格下的误差大小Table 1 Discretization error using three grids 图2 3种尺寸网格的计算波面高度曲线Fig.2 Computational wave elevation using three grids 为验证建立的数值波浪水槽准确性,首先对无射流条件下波浪水槽进行数值模拟计算。图3给出了波高H=0.10 m、波周期T=1.5 s条件下,距离波浪水槽造波端9 m处稳定后的规则波波面时程曲线和理论值的对比。可以看出,数值计算波面与理论波面变化趋势比较吻合,相对误差均在5%以内。数值计算中波高出现轻微衰减的现象,这是由于数学模型水体存在一定的黏性损耗,本文建立的三维数值波浪水槽是可靠的。 图3 波面时程曲线验证Fig.3 Wave surface elevation history validation 图4给出了静水和规则波(H=0.10 m,T=1.5 s,D=0.015 m,wj=1.57 m/s)条件下射流中轴(经过射流口中心点的垂线)上的量纲一平均垂向速度(w0/wj)计算值与试验值,其中利用相位平均法得到射流中轴上某一点的平均垂向速度w0。发现随着射流距离的增加,平均垂向速度相应降低,计算值与试验数据吻合较好,说明本文建立的规则波作用下负浮力射流模型合理可靠,可以进行后续的计算工作。 图4 射流中轴上量纲一平均垂向速度验证Fig.4 Verification of the dimensionless average vertical velocity at the jet axis 基于验证后的数学模型,对不同规则波参数下负浮力射流的水动力行为进行计算,其中射流口直径D=0.015 m,射流口速度wj=1.57 m/s,ρj=1 050 kg/m3,ρa=1 000 kg/m3。工况1为静水无波浪条件,其他工况波高和波周期组合分别为:工况2(0.06 m,1.5 s)、工况3(0.08 m,1.5 s)、工况4(0.10 m,1.5 s)、工况5(0.12 m,1.5 s)、工况6(0.10 m,1.2 s)、工况7(0.10 m,1.8 s)、工况8(0.10 m,2.1 s)。 图5给出了T=1.5 s、H=0.10 m工况4射流口中心所在纵剖面(y=0)上4个典型时刻的浓度场和速度场分布。可以看出,上述4个时刻,远离波面的射流口附近流向基本呈现向上状态,且流速较大。规则波上跨零点时刻(t=T/4),受波面上升水质点影响,距离射流口较远处的流向基本呈现向上状态,入射波带动射流流体向上运动。波峰时刻(t=T/2),波面水质点运动方向与波浪传播方向一致,距离射流口较远处的流速基本偏向正x方向;从入射波上跨零点到波峰期间,波面附近水质点运动带动射流轴向正x方向摆动。下跨零点时刻(t=3T/4),受波面下降水质点影响,距离射流口较远处的流向基本呈现垂直向下状态,带动射流顶端云团向下运动。波谷时刻(t=T),波面水质点运动方向与波浪传播方向相反,距离射流口较远的流向基本偏向负x方向;从下跨零点到波谷期间,波面附近水质点流向的改变带动射流轴向负x方向摆动。总体来看,波浪运动带动了射流轴的摆动,加快了射流流体与环境水体的掺混,有助于射流流体稀释和扩散。 图5 y=0纵剖面上典型时刻水体速度场和浓度场分布Fig.5 Velocity field and concentration field distribution at typical times under y=0 longitudinal section 图6(a)给出了T=1.5 s时,不同波高条件下射流中轴上量纲一平均垂向速度(w0/wj)与量纲一射流距离(z/D)的关系曲线。可以看出,随着波高增加,w0/wj相应降低,射流中轴上平均垂向速度w0衰减加快。从图中还可以看出,z/D<10时,w0/wj衰减较快;z/D>10时,射流初始动量的影响相对较小,负浮力和波浪的影响逐渐增加,其衰减速度趋缓,可以用经验公式(12)[15]来描述。 (12) 式中:B和n是衰减系数和指数,分别表示射流中轴上量纲一平均垂向速度衰减的早晚和衰减率。随着B值增加,射流中轴上任一点平均垂向速度衰减程度降低,即衰减越晚;随着n值增加,射流中轴上任两点的平均垂向速度差值减小,即衰减率减小。 图6(b)给出了图6(a)工况下z/D>10范围内的w0/wj数据;为了与纯水射流试验进行对比,这里引用了文献[16]在规则波作用下观测的试验数据。基于公式(12),对文献[16]试验数据和本文计算值拟合得到的衰减指数n分别为-1.07和-1.65~-1.75,本文的n值变化不大,说明波高对平均垂向速度沿射流中轴的衰减率影响不大。由于负浮力加快了射流轴上垂向速度衰减,本文w0/wj小于文献[16]的试验数据。另外,相应拟合线相关系数较高,说明w0/wj与z/D的关联度较好。为分析方便,对本文计算值进行拟合时n取-1.65和-1.75的均值-1.70,得到0.06 m、0.08 m、0.10 m和0.12 m波高条件下对应的B值分别为19.41、16.42、13.39和10.41,上述B值迅速减小,差值也较大,说明波高对平均垂向速度沿射流中轴衰减的早晚有较大影响;波高越大,w0/wj衰减越早。 图6 不同波高条件下射流中轴上量纲一平均垂向速度分布Fig.6 Dimensionless average vertical velocity distribution along the jet axis under various wave heights 图7给出了T=1.5 s时,距离射流口不同距离水平剖面的纵轴线上量纲一平均垂向速度(w/w0)分布,其中w为某一点的平均垂向速度。可以看出,距离射流口较近时,其分布基本符合高斯分布,具有一定的自相似性。随着远离射流口,w/w0分布范围逐渐变宽。波高从H=0.08 m增加到0.10 m和0.12 m时,z值较大剖面上的w/w0开始呈现双峰分布,这是由于较强的波浪振荡引起射流中轴较大幅度的摆动引起的。随着波高增加,射流扩展率相应增加,开始出现双峰的水平剖面也更加靠近射流口。z值较大的水平剖面上,远离射流中轴的w/w0出现了负值,这可能是此处距离射流口较远,射流初始动量对其影响相对较小,而射流盐水密度大于清水造成的负浮力影响较大造成的。 图7 距离射流口不同距离的水平剖面纵轴线上量纲一平均垂向速度分布Fig.7 Dimensionless average vertical velocities along the longitudinal line at horizontal sections with different distances from the jet exit 图8为T=1.5 s、不同波高条件下量纲一射流特征速度半宽(bw/D)与量纲一垂向距离(z/D)的关系,这里bw定义为水平剖面纵轴线上w0/wj=0.5所对应的2个x值之差的一半。可以看出,随着z/D的增加,静水和波浪条件下的bw/D均相应增加;静水条件下的bw/D与z/D基本呈现线性关系。z/D<5时,静水和波浪条件下的bw基本一致,原因是在这段区域内射流主要受射流初始动量影响,波浪和负浮力对其影响较小;z/D>5时,随着波高增加,bw和射流扩展率相应增加,这是由于射流初始动量影响沿程衰减,波浪和负浮力对射流影响逐渐增加造成的。 图8 不同波高条件下射流特征速度半宽与量纲一垂向距离关系Fig.8 Half width of jet velocity relationships with dimensionless vertical distance under various wave heights 图9(a)为H=0.10 m、不同波周期条件下射流中轴上量纲一平均垂向速度(w0/wj)的变化。可以看出,随着波周期增加,w0/wj相应降低,射流中轴上垂向速度衰减越明显;z/D<10时,w0/wj衰减较快;z/D>10时,其衰减速度趋缓。图9(b)给出了图9(a)工况下z/D>10范围内的w0/wj数据,为了与纯水射流试验进行对比,同样引用了文献[16]在规则波作用下观测的试验数据。基于公式(12),分别对文献[16]试验数据和本文计算值进行拟合,得到n分别为-1.07和-1.61~-1.80,本文的n值变化不大,说明波周期对平均垂向速度沿射流中轴的衰减率影响不大。另外,相应拟合线相关系数较高,说明w0/wj与z/D的关联度较好,这也与图6(b)给出的趋势相吻合。为分析方便,对本文计算值进行拟合时n取-1.61和-1.80的近似均值-1.70,得到波周期由1.2 s增加到1.5 s、1.8 s和2.1 s时,所对应的衰减系数B值分别从17.34降低到13.39、10.13和8.34,差别也较大。可以看出,波周期对平均垂向速度沿射流中轴衰减的早晚有较大影响,波周期越大,w0/wj衰减越早。 图9 不同波周期条件下射流中轴上量纲一平均垂向速度分布Fig.9 Dimensionless average vertical velocity distribution along the jet axis under various wave periods 图10为H=0.10 m、不同波周期条件下射流特征速度半宽沿射流中轴相对距离(z/D)的变化。可以看出,随着z/D的增加,静水和波浪条件下的bw均相应增加;静水条件下的bw/D与z/D基本呈现线性关系。z/D<5时,静水和波浪条件下的bw基本一致,原因是在这段区域内射流主要受射流初始动量影响,波浪和负浮力对其影响较小。z/D>5时,随着波周期增加,bw相应增加;波周期T=2.1 s时,z/D=7时bw急剧增加,在z/D=13.33处其增幅开始趋于平缓,这是由于波周期较大的工况下射流轴发生了明显偏折。 图10 不同波周期条件下射流特征速度半宽与量纲一垂向距离关系Fig.10 Characteristic velocity half-width relationship with the dimensionless vertical distance under various wave periods Mori和Chang[8]引入波-射流动量比(RM)参数研究波浪环境下非浮力射流的振荡特性: (13) 式中:A为波幅,m。 本研究中射流流体和环境水体之间存在着一定密度差,这里引入环境流体与射流流体的密度比ρa/ρj,对公式(13)进行改写,得到考虑浮力效应的波-射流动量比(RMB): (14) 图11为各计算工况下衰减系数(B)与RMB的关系和拟合直线(其拟合公式形式为B=C1RMB+C2,C1和C2为系数)。从图11(a)可以看出,波周期一定情况下,随着波高或波幅增加,RMB增加,B值相应降低,两者呈负相关关系。从图11(b)可以看出,波高一定情况下,随着波周期增加,RMB和B值均相应减小,两者呈正相关关系。可见,随着波高和波周期增加,平均垂向速度沿射流中轴衰减的越早,稀释和扩散效果也越好。 图11 衰减系数与波-射流动量比的关系Fig.11 Relationship between decay coefficient and wave-to-jet momentum ratio 图12为各组工况下射流平均特征速度半宽(b/D)与RMB的关系曲线和拟合直线(其拟合公式形式为b/D=D1RMB+D2,D1和D2为系数),b由公式(15)给出,其中Zmax和Zmin分别为Z方向计算域的最大和最小值。从图12(a)可以看出,波周期一定情况下,随着波高或波幅增加,RMB和b/D值均相应增加,两者呈正相关关系。从图12(b)可以看出,波高一定情况下,随着波周期增加,RMB减小,b/D值相应增加,两者呈负相关关系。可见,波浪对射流的扩展率有较明显的影响;随着波高和波周期增加,射流平均特征速度半宽增加,有利于射流盐水的稀释和扩散。 图12 平均特征速度半宽与波-射流动量比的关系Fig.12 Relationship between average characteristic velocity half-width and wave-to-jet momentum ratio (15) 本文通过物理模型试验和数值模拟相结合的方法,开展了规则波作用下垂直圆管负浮力射流特性研究,探讨了波参数、波射流动量比与射流特性之间的关系。得到以下结论: (1)规则波作用下垂直圆管负浮力射流的数值模拟计算结果与试验结果较吻合,说明建立的数学模型是合理可靠的。 (2)波高和周期对平均垂向速度沿射流中轴的衰减指数影响不大,而对衰减系数影响较大。随着波高或波周期的增加,射流特征速度半宽增加,射流中轴上垂向速度的衰减系数减小。波浪促进了射流的振荡,有助于射流流体与环境水体的混合,提高了射流流体的扩散稀释效率。 (3)波周期一定、波高变化条件下,射流中轴上量纲一平均垂向速度衰减系数与考虑浮力效应的波-射流动量比呈负相关关系,平均特征速度半宽与考虑浮力效应的波-射流动量比呈正相关关系。波高一定、波周期变化条件下,射流中轴上量纲一平均垂向速度衰减系数与考虑浮力效应的波-射流动量比呈正相关关系,平均特征速度半宽与考虑浮力效应的波-射流动量比呈负相关关系。另外,建立了考虑浮力效应的波-射流动量比表征的衰减系数和平均特征速度半宽公式,可对高浓度盐水排放高度及扩展范围进行相关预测分析。 需要说明的是,本研究选取的数值计算尺度都是以室内试验条件为基础的,入射波也选取相对简单的规则波,与实际海况存在较大区别。下一步需要对实际复杂海况条件下的负浮力射流特性进行深入研究。1.2 边界条件

2 物理模型试验及数学模型验证
2.1 物理模型试验

2.2 网格独立性验证


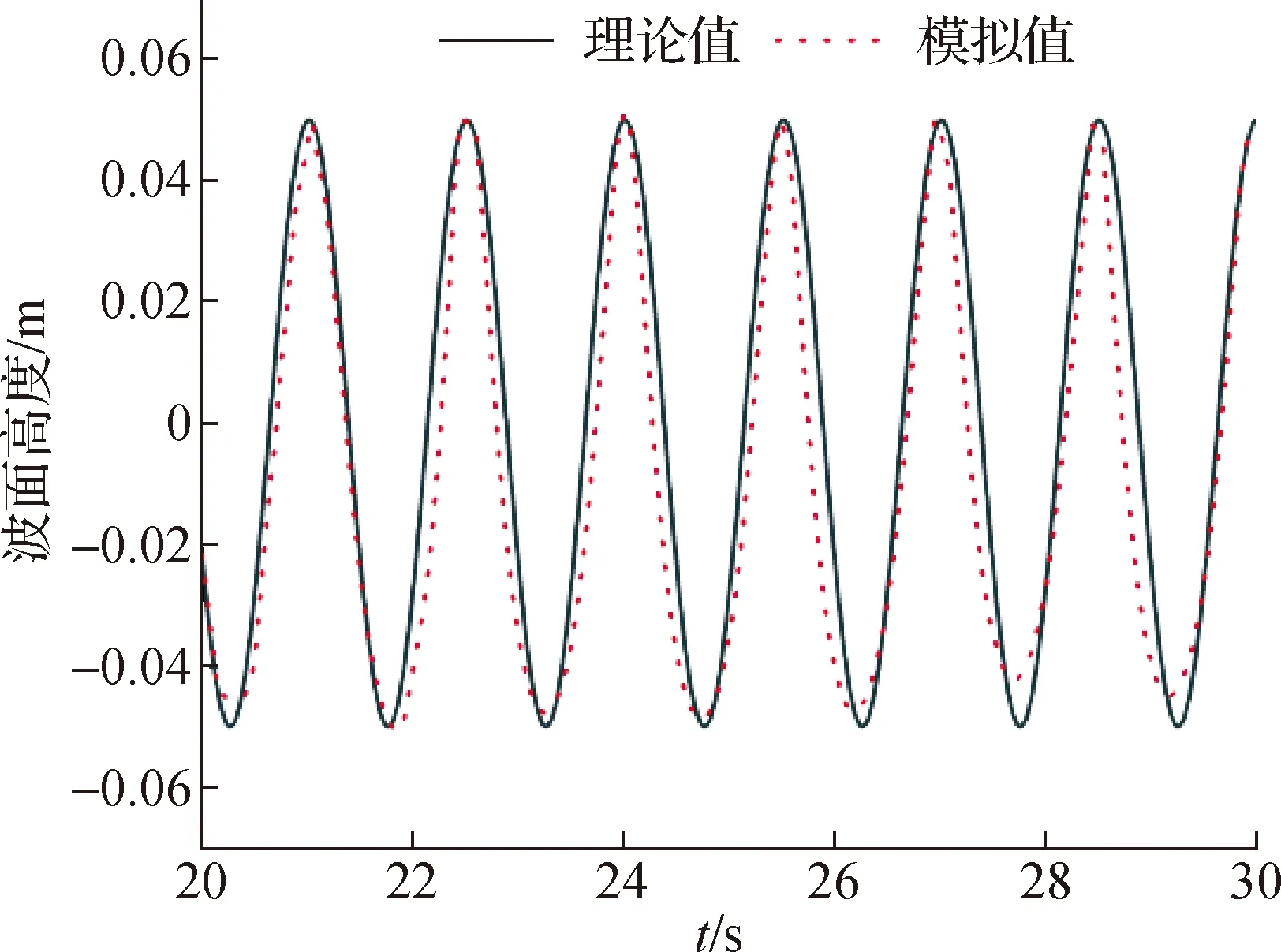
2.3 三维波浪水槽验证
2.4 负浮力射流数值模拟的验证

3 计算结果与分析
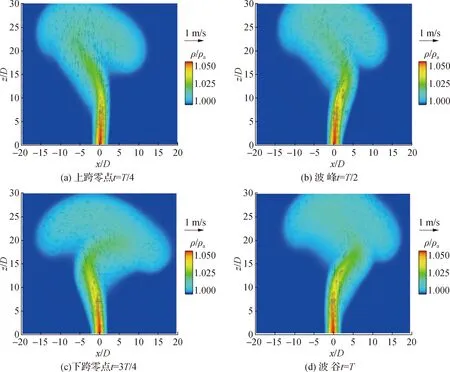
3.1 射流浓度场和速度场分布
3.2 波高对射流特性的影响



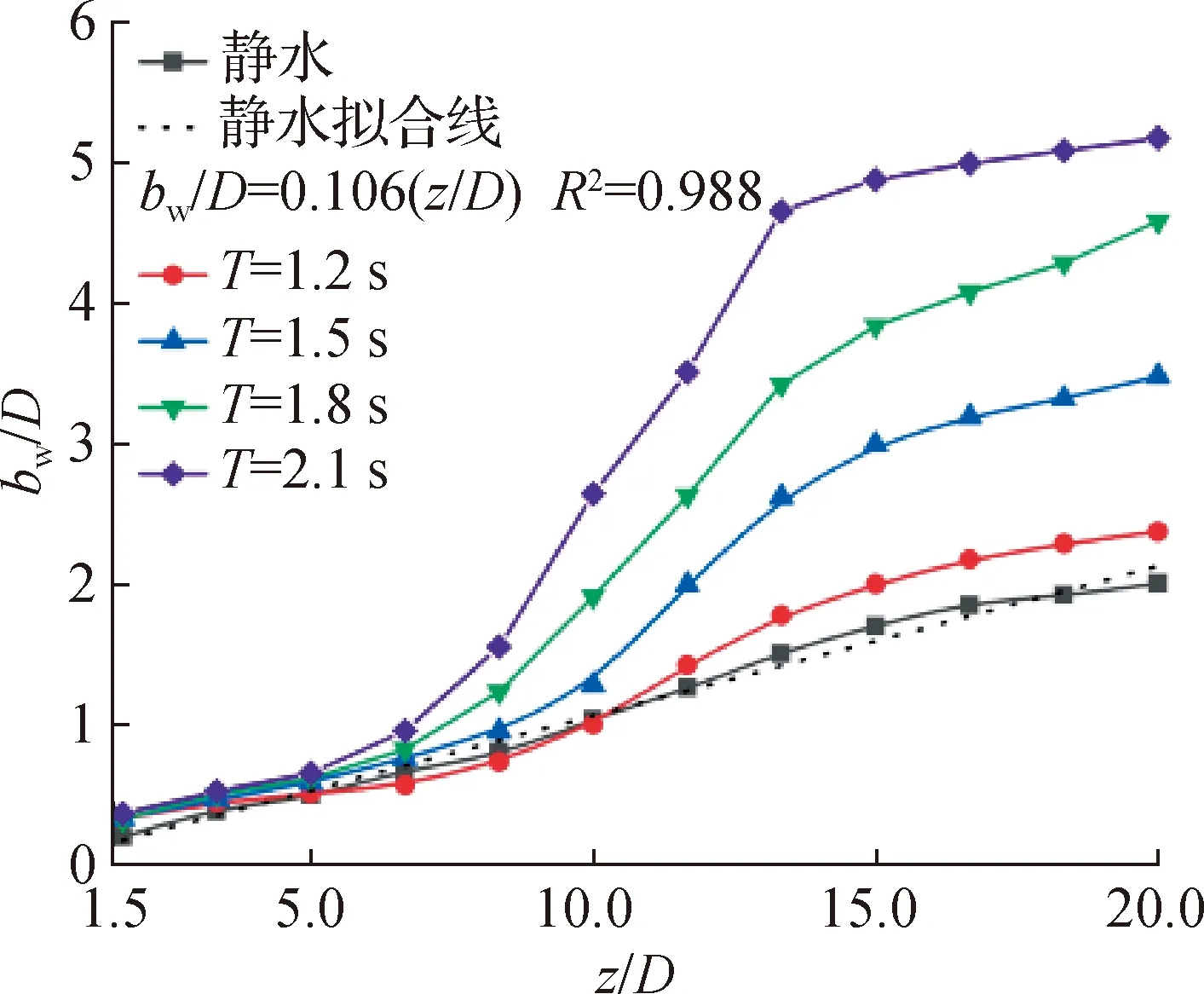
3.3 波周期对射流特性的影响

3.4 波-射流动量比与射流特性的关系


4 结 论
——以匀加速直线运动公式为例

